library(tidyverse)
library(labelled)
library(gtsummary)
theme_gtsummary_language(
"fr",
decimal.mark = ",",
big.mark = " "
)
data(hdv2003, package = "questionr")
d <-
hdv2003 |>
mutate(
sexe = sexe |> fct_relevel("Femme"),
groupe_ages = age |>
cut(
c(18, 25, 45, 65, 99),
right = FALSE,
include.lowest = TRUE,
labels = c("18-24 ans", "25-44 ans",
"45-64 ans", "65 ans et plus")
),
etudes = nivetud |>
fct_recode(
"Primaire" = "N'a jamais fait d'etudes",
"Primaire" = "A arrete ses etudes, avant la derniere annee d'etudes primaires",
"Primaire" = "Derniere annee d'etudes primaires",
"Secondaire" = "1er cycle",
"Secondaire" = "2eme cycle",
"Technique / Professionnel" = "Enseignement technique ou professionnel court",
"Technique / Professionnel" = "Enseignement technique ou professionnel long",
"Supérieur" = "Enseignement superieur y compris technique superieur"
) |>
fct_na_value_to_level("Non documenté")
) |>
set_variable_labels(
sport = "Pratique un sport ?",
sexe = "Sexe",
groupe_ages = "Groupe d'âges",
etudes = "Niveau d'études",
heures.tv = "Heures de télévision / jour"
)
mod <- glm(
sport ~ sexe + groupe_ages + etudes + heures.tv,
family = binomial,
data = d
)24 Prédictions marginales, contrastes marginaux & effets marginaux
Les coefficients d’une régression multivariable ne sont pas toujours facile à interpréter car ils ne sont pas forcément exprimés dans la même dimension que la variable d’intérêt. C’est notamment le cas pour une régression logistique binaire (cf. Chapitre 22). Comment traduire la valeur d’un odds ratio en écart de probabilité ?
Dans certaines disciplines, notamment en économétrie, on préfère souvent présenter les effets marginaux
qui tentent de traduire les résultats du modèle dans la dimension de la variable d’intérêt. Plusieurs approches existent et l’on trouve dans la littérature des expressions telles que effets marginaux
, effets statistiques
, moyennes marginales
, pentes marginales
, effets marginaux à la moyenne
, et autres expressions similaires.
Différents auteurs peuvent utiliser la même expression pour désigner des indicateurs différents, ou bien des manières différentes de les calculer.
Note
Si vous n’êtes pas familier des estimations marginales et souhaitez aller à l’essentiel, vous pouvez, en première lecture, vous concentrer sur les prédications marginales moyennes et les contrastes marginaux moyens, avant d’explorer les autres variantes.
24.1 Terminologie
Dans ce guide, nous avons décidé d’adopter une terminologie consistante avec celle du package broom.helpers, elle même basée sur celle du package {marginaleffects}, dont la première version a été publié en septembre 2021, et avec le billet d’Andrew Heiss intitulé Marginalia et publié en mai 2022.
Lorsque l’on utilise un modèle ajusté pour prédire l’outcome selon certaines combinaisons de valeurs des régresseurs / variables explicatives, par exemple leurs valeurs observées ou leur moyenne, on obtient des prédictions ajustées. Lorsque ces dernières sont moyennées selon un régresseur spécifique, nous parlerons alors de prédictions marginales.
Les contrastes marginaux correspondent au calcul d’une différence entre des prédictions marginales, que ce soit pour une variable catégorielle (e.g. différence entre deux modalités) ou pour une variable continue (différence observée au niveau de l’outcome pour un certain changement du prédicteur).
Les pentes marginales ou effets marginaux sont définis, pour des variables continues, comme la dérivée partielle (slope) de l’équation de régression pour certains valeurs de la variable explicative. Dit autrement, un effet marginal correspond à la pente locale de la fonction de régression pour certaines valeurs choisies d’un prédicteur continue. De manière pratique, les effets marginaux sont similaires aux contrastes marginaux.
L’ensemble de ces indicateurs marginaux se calculent pour certaines valeurs typiques
des variables explicatives, avec plusieurs approches possibles pour définir des valeurs typiques
: moyenne / mode, valeurs observées, valeurs personnalisées…
Nous présenterons ces différents concepts plus en détail dans la suite de ce chapitre.
Plusieurs packages proposent des fonctions pour le calcul d’estimations marginales, marginaleffects, emmeans, margins, effects, ou encore ggeffects, chacun avec des approches et un vocabulaire légèrement différent.
Le package broom.helpers fournit plusieurs tidiers
qui permettent d’appeler les fonctions de ces autres packages et de renvoyer un tableau de données compatible avec la fonction broom.helpers::tidy_plus_plus() et dès lors de pouvoir générer un tableau mis en forme avec gtsummary::tbl_regression() ou un graphique avec ggstats::ggcoef_model().
24.2 Données d’illustration
Pour illustrer ce chapitre, nous allons prendre un modèle logistique issu du chapitre sur la régression logistique binaire (cf. Chapitre 22).
Caractéristique |
OR 1 |
95% IC 1 |
p-valeur |
|---|---|---|---|
| Sexe | |||
| Femme | — | — | |
| Homme | 1,52 | 1,24 – 1,87 | <0,001 |
| Groupe d'âges | |||
| 18-24 ans | — | — | |
| 25-44 ans | 0,68 | 0,43 – 1,06 | 0,084 |
| 45-64 ans | 0,36 | 0,23 – 0,57 | <0,001 |
| 65 ans et plus | 0,27 | 0,16 – 0,46 | <0,001 |
| Niveau d'études | |||
| Primaire | — | — | |
| Secondaire | 2,54 | 1,73 – 3,75 | <0,001 |
| Technique / Professionnel | 2,81 | 1,95 – 4,10 | <0,001 |
| Supérieur | 6,55 | 4,50 – 9,66 | <0,001 |
| Non documenté | 8,54 | 4,51 – 16,5 | <0,001 |
| Heures de télévision / jour | 0,89 | 0,83 – 0,95 | <0,001 |
|
1
OR = rapport de cotes, IC = intervalle de confiance |
|||
Il faut se rappeler que pour calculer le modèle, les observations ayant au moins une valeur manquante ont été exclues. Le modèle n’a donc pas été calculé sur 2000 observations (nombre de lignes de hdv2003) mais sur 1995. On peut obtenir le tableau de données du modèle (model frame), qui ne contient que les variables et les observations utilisées, avec broom.helpers::model_get_model_frame().
24.3 Prédictions marginales
24.3.1 Prédictions marginales moyennes
Pour illustrer et mieux comprendre ce que représente la différence entre les femmes et les hommes, nous allons effectuer des prédictions avec notre modèle en ne faisant varier que la variable sexe.
Une première approche consiste à dupliquer nos données observées et à supposer que tous les individus sont des femmes, puis à supposer que tous les individus sont des hommes.
Nos deux jeux de données sont donc identiques pour toutes les autres variables et ne varient que pour le sexe. Nous pouvons maintenant prédire, à partir de notre modèle ajusté, la probabilité de faire du sport de chacun des individus de ces deux nouveaux jeux de données, puis à en calculer la moyenne.
[1] 0.324814[1] 0.4036624Nous obtenons ainsi des prédictions marginales moyennes, average marginal predictions en anglais, de respectivement 32% et 40% pour les femmes et pour les hommes.
Le même résultat, avec en plus un intervalle de confiance, peut s’obtenir avec marginaleffects::predictions().
sexe Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
Femme 0.325 0.0130 25.0 <0.001 456.7 0.299 0.350
Homme 0.404 0.0147 27.5 <0.001 549.0 0.375 0.432
Columns: sexe, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high
Type: response Pour une variable continue, on peut procéder de la même manière en générant des prédictions marginales pour certaines valeurs de la variable. Par défaut, marginaleffects::predictions() réalise des prédictions selon les 5 nombres de Tukey (Tukey’s five numbers, à savoir minimum, premier quartile, médiane, troisième quartile et maximum).
heures.tv Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
0 0.410 0.01711 23.96 <0.001 419.0 0.3764 0.443
1 0.386 0.01220 31.64 <0.001 727.2 0.3621 0.410
2 0.363 0.00991 36.58 <0.001 970.7 0.3432 0.382
3 0.340 0.01145 29.66 <0.001 639.9 0.3173 0.362
12 0.168 0.04220 3.99 <0.001 13.9 0.0855 0.251
Columns: heures.tv, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high
Type: response Le package broom.helpers fournit la fonction broom.helpers::tidy_marginal_predictions() qui génèrent les prédictions marginales de chaque variable1 avec marginaleffects::predictions() et renvoie les résultat dans un format directement utilisable avec gtsummary::tbl_regression().
1 La fonction broom.helpers::tidy_marginal_predictions() peut également gérer des combinaisons de variables ou interactions, voir Chapitre 26).
Note
Il est à noter que broom.helpers::tidy_marginal_predictions() renvoie des p-valeurs qui, par défaut, teste si les valeurs prédites sont différentes de 0 (sur l’échelle de la fonction de lien, donc différentes de 50% dans le cas d’une régression logistique). Ce type de tests n’est pas vraiment pertinent dans le cas présent. On peut facilement masquer la colonne des p-valeurs avec modify_column_hide("p.value").
mod |>
tbl_regression(
tidy_fun = broom.helpers::tidy_marginal_predictions,
type = "response",
estimate_fun = scales::label_percent(accuracy = 0.1)
) |>
bold_labels() |>
modify_column_hide("p.value")Caractéristique |
Prédictions Marginales Moyennes |
95% IC 1 |
|---|---|---|
| Sexe | ||
| Femme | 32.5% | 29.9% – 35.0% |
| Homme | 40.4% | 37.5% – 43.2% |
| Groupe d'âges | ||
| 18-24 ans | 51.2% | 42.2% – 60.1% |
| 25-44 ans | 42.7% | 39.3% – 46.2% |
| 45-64 ans | 29.9% | 26.6% – 33.2% |
| 65 ans et plus | 24.9% | 19.7% – 30.0% |
| Niveau d'études | ||
| Primaire | 16.1% | 11.9% – 20.4% |
| Secondaire | 31.8% | 27.2% – 36.4% |
| Technique / Professionnel | 34.0% | 30.3% – 37.7% |
| Supérieur | 53.2% | 48.4% – 57.9% |
| Non documenté | 59.2% | 47.0% – 71.5% |
| Heures de télévision / jour | ||
| 0 | 41.0% | 37.6% – 44.3% |
| 1 | 38.6% | 36.2% – 41.0% |
| 2 | 36.3% | 34.3% – 38.2% |
| 3 | 34.0% | 31.7% – 36.2% |
| 12 | 16.8% | 8.6% – 25.1% |
|
1
IC = intervalle de confiance |
||
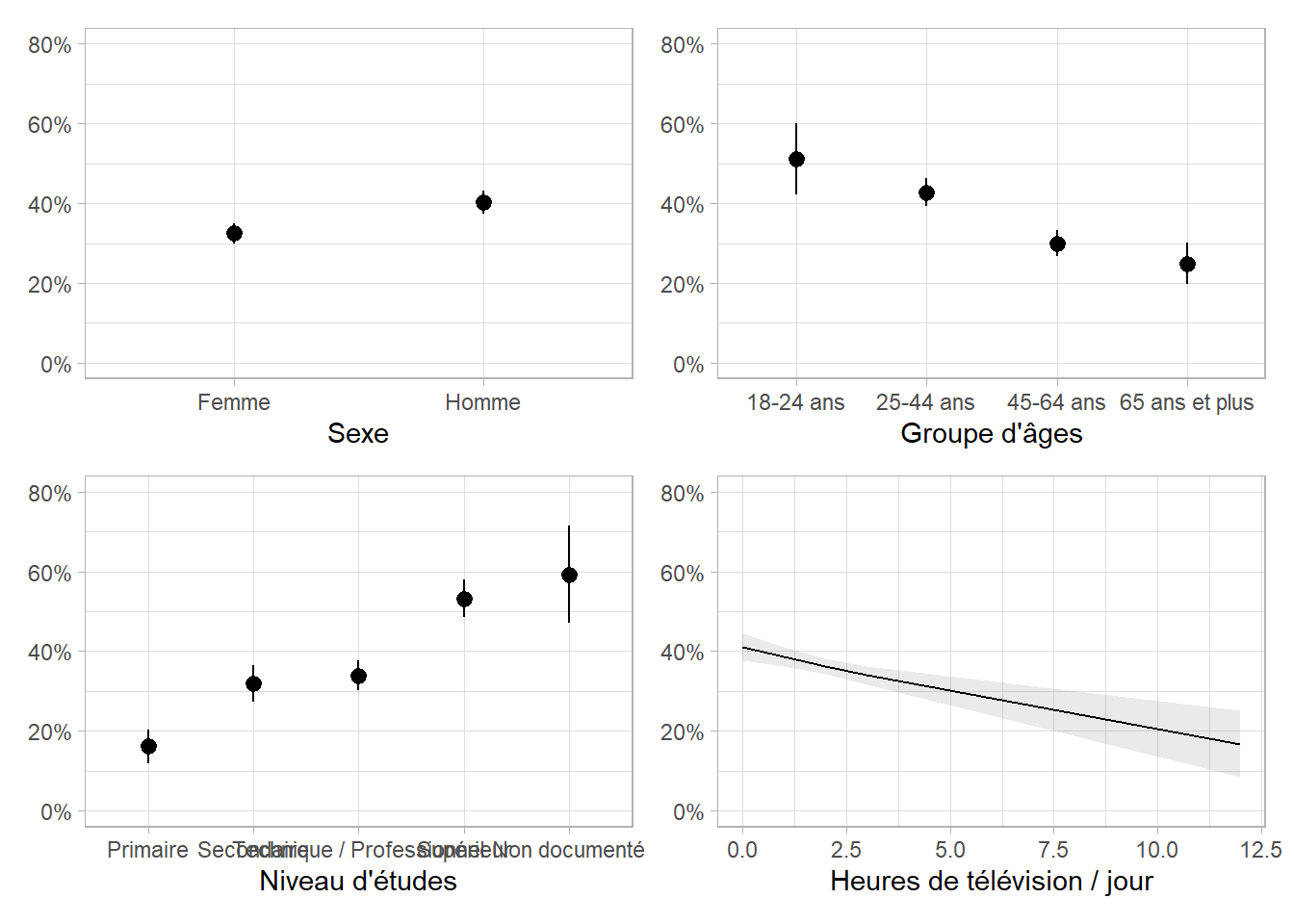
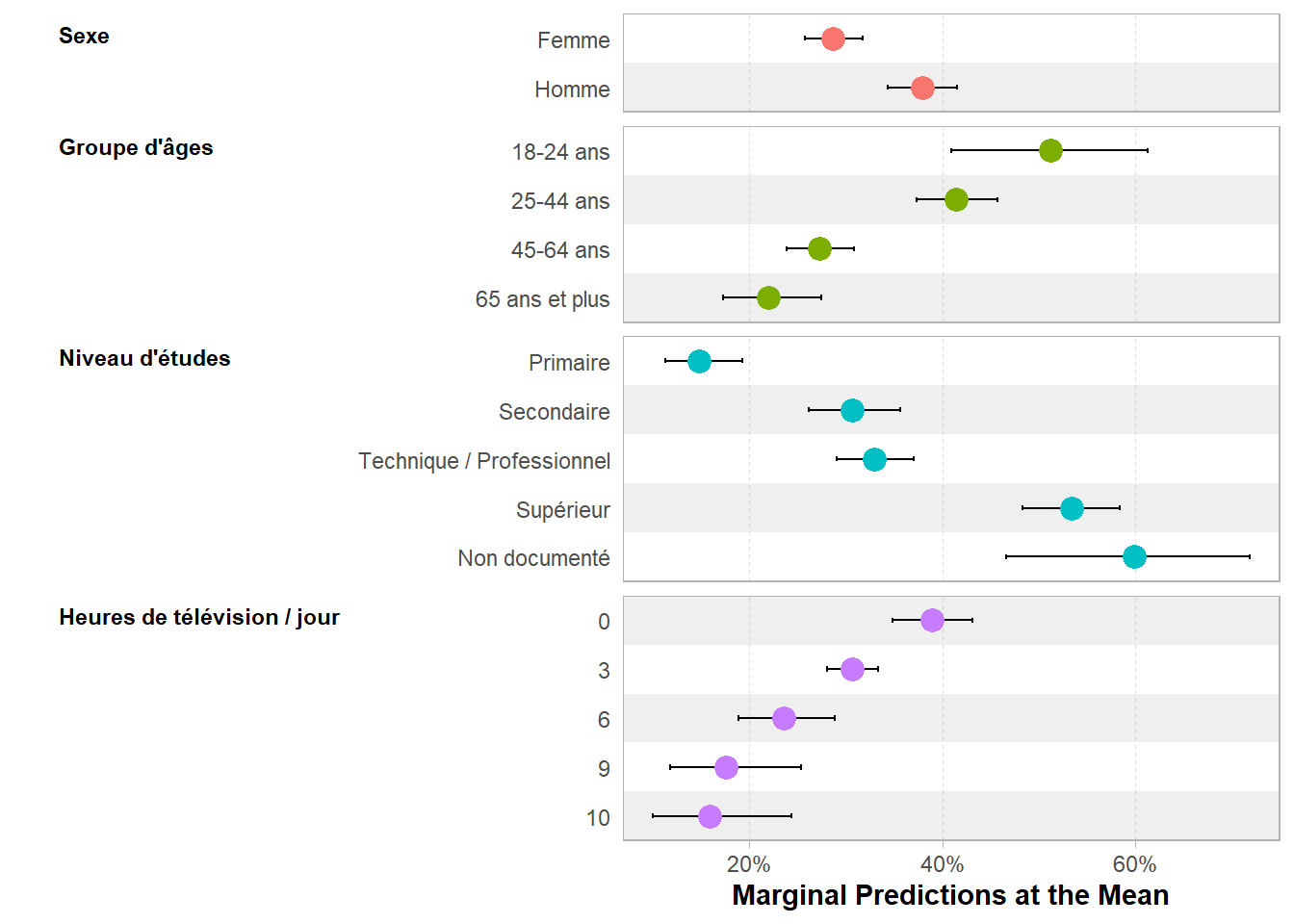
La fonction broom.helpers::plot_marginal_predictions() permet de visualiser les prédictions marginales à la moyenne en réalisant une liste de graphiques, un par variable, que nous pouvons combiner avec patchwork::wrap_plots(). L’opérateur & permet d’appliquer une fonction de ggplot2 à chaque sous-graphique. Ici, nous allons uniformiser l’axe des y.
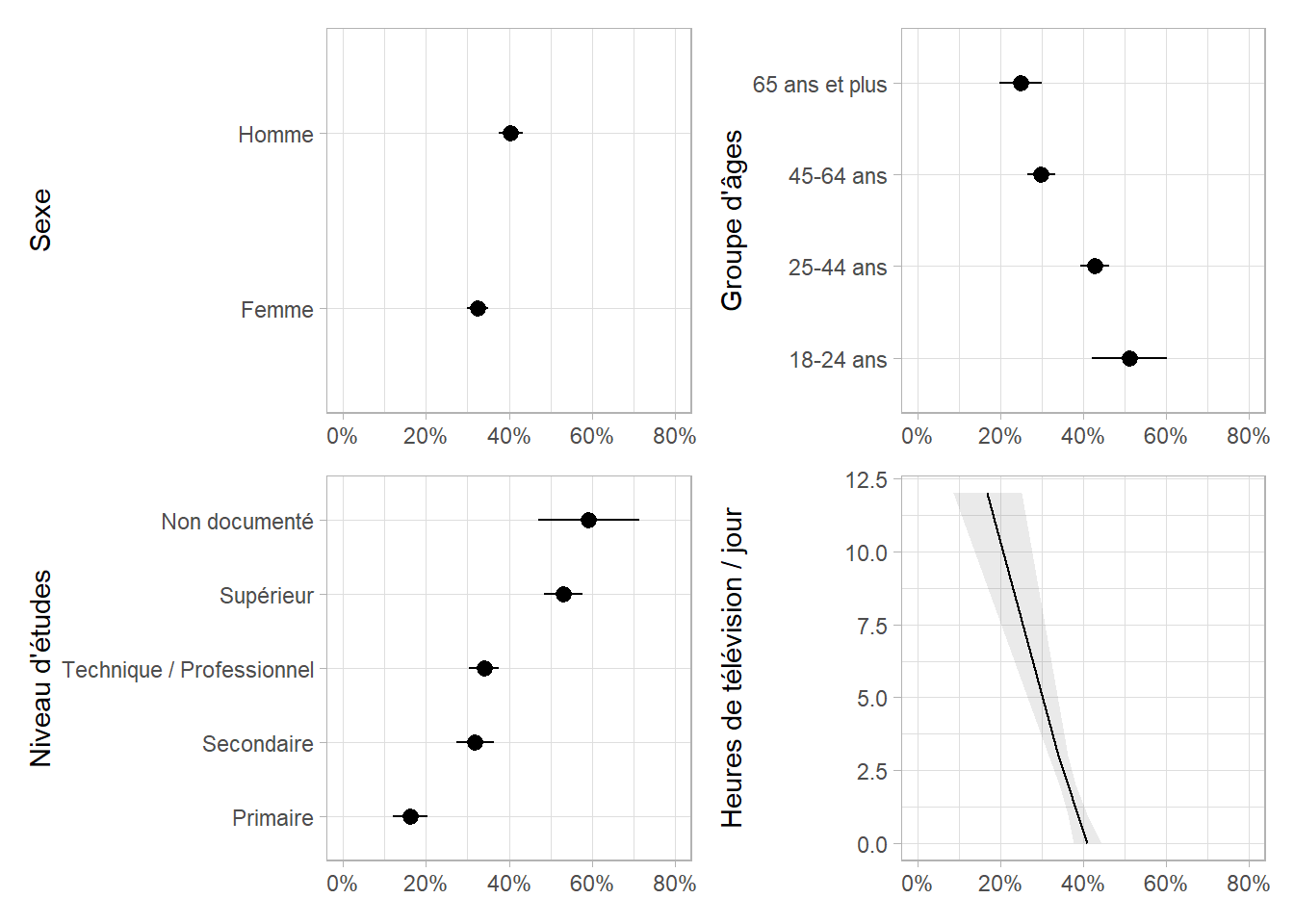
Il est ici difficile de lire les étiquettes de la variable etudes. Nous pouvons éventuellement inverser l’axe des x et celui des y avec ggplot2::coord_flip().
Une alternative possible avec d’avoir recours à ggtstats::ggcoef_model().
mod |>
ggstats::ggcoef_model(
tidy_fun = broom.helpers::tidy_marginal_predictions,
tidy_args = list(type = "response"),
show_p_values = FALSE,
signif_stars = FALSE,
significance = NULL,
vline = FALSE
) +
scale_x_continuous(labels = scales::label_percent())
Importance de l’argument
type pour les modèles glm
Lorsque l’on a recours à des modèles calculés avec glm(), il est possible de réaliser des prédictions selon deux échelles : l’échelle de notre outcome ou variable à expliquer (type = "response"), ici exprimée en probabilités ou proportions puisqu’il s’agit d’une régression logistique, ou bien selon l’échelle de la fonction de lien (type = "link") du modèle, ici la fonction logit (voir Section 22.4).
Avec l’option type = "reponse", on indique à marginaleffects de calculer pour chaque individu une prédiction selon l’échelle de l’outcome puis de procéder à la moyenne, ce que nous avons fait dans les exemples précédents.
Si nous avions indiqué type = "link", les prédictions auraient été faites selon l’échelle de la fonction de lien avant d’être moyennée.
[1] -0.910525[1] -0.4928844
sexe Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
Femme -0.911 0.0751 -12.13 <0.001 110.0 -1.058 -0.763
Homme -0.493 0.0779 -6.33 <0.001 31.9 -0.646 -0.340
Columns: sexe, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high
Type: link Depuis la version 0.10.0 de marginaleffects, si l’on ne précise pas le paramètre type (i.e. si type = NULL), la fonction marginaleffects::predictions() réalise les prédictions selon l’échelle de la fonction de lien, calcule les moyennes puis re-transforme ce résultat selon l’échelle de la variable à expliquer.
logit_inverse <- binomial("logit") |> purrr::pluck("linkinv")
mod |> predict(type = "link", newdata = mf_femmes) |> mean() |> logit_inverse()[1] 0.2868924[1] 0.3792143
sexe Estimate Pr(>|z|) S 2.5 % 97.5 %
Femme 0.287 <0.001 110.0 0.258 0.318
Homme 0.379 <0.001 31.9 0.344 0.416
Columns: sexe, estimate, p.value, s.value, conf.low, conf.high
Type: invlink(link) Or, la plupart du temps, le logit inverse de la moyenne des prédictions est différent de la moyenne des logit inverse des prédictions !
Les résultats seront similaires et du même ordre de grandeur, mais pas identiques.
24.3.2 Prédictions marginales à la moyenne
Pour les prédictions marginales moyennes, nous avons réalisé des prédictions pour chaque observations du tableau d’origine, en faisant varier juste une variable à la fois, avant de calculer la moyenne des prédictions.
Une alternative consiste à générer une sorte d’individu moyen / typique
puis à réaliser des prédictions pour cette unique individu, en faisant juste varier la variable explicative d’intérêt. On parle alors de prédictions marginales à la moyenne, marginal predictions at the mean en anglais.
24.3.2.1 avec {marginaleffects}
On peut réaliser cela avec marginaleffects en précisant newdata = "mean". Prenons un exemple pour la variable sexe :
groupe_ages etudes heures.tv sexe Estimate Pr(>|z|) S
45-64 ans Technique / Professionnel 2.25 Femme 0.239 <0.001 59.5
45-64 ans Technique / Professionnel 2.25 Homme 0.323 <0.001 29.5
2.5 % 97.5 %
0.196 0.289
0.273 0.378
Columns: rowid, rowidcf, estimate, p.value, s.value, conf.low, conf.high, sport, groupe_ages, etudes, heures.tv, sexe
Type: invlink(link) Dans ce cas de figure, marginaleffects considère pour chaque variable continue sa moyenne (ici 2.246 pour heures.tv) et pour chaque variable catégorielle son mode (la valeur observée la plus fréquente, ici "Technique / Professionnel" pour la variable etudes). On fait juste varier les modalités de sexe puis on calculer la probabilité de faire du sport de ces individus moyens.
On peut également passer le paramètre newdata = "mean" à broom.helpers::tidy_marginal_predictions() ou même à gtsummary::tbl_regression()2.
2 Les paramètres additionnels indiqués à gtsummary::tbl_regression() sont transmis en cascade à broom.helpers::tidy_plus_plus() puis à broom.helpers::tidy_marginal_predictions() et enfin à marginaleffects::predictions().
mod |>
tbl_regression(
tidy_fun = broom.helpers::tidy_marginal_predictions,
newdata = "mean",
estimate_fun = scales::label_percent(accuracy = 0.1)
) |>
bold_labels() |>
modify_column_hide("p.value")Caractéristique |
Prédictions Marginales à la Moyenne |
95% IC 1 |
|---|---|---|
| Sexe | ||
| Femme | 23.9% | 19.6% – 28.9% |
| Homme | 32.3% | 27.3% – 37.8% |
| Groupe d'âges | ||
| 18-24 ans | 46.8% | 36.1% – 57.8% |
| 25-44 ans | 37.3% | 32.1% – 42.8% |
| 45-64 ans | 23.9% | 19.6% – 28.9% |
| 65 ans et plus | 19.2% | 14.0% – 25.6% |
| Niveau d'études | ||
| Primaire | 10.1% | 7.3% – 13.7% |
| Secondaire | 22.1% | 17.7% – 27.2% |
| Technique / Professionnel | 23.9% | 19.6% – 28.9% |
| Supérieur | 42.3% | 36.0% – 48.9% |
| Non documenté | 48.9% | 34.7% – 63.2% |
| Heures de télévision / jour | ||
| 0 | 29.2% | 23.6% – 35.5% |
| 1 | 26.8% | 21.9% – 32.3% |
| 2 | 24.5% | 20.1% – 29.5% |
| 3 | 22.3% | 18.1% – 27.2% |
| 12 | 8.8% | 4.6% – 16.4% |
|
1
IC = intervalle de confiance |
||
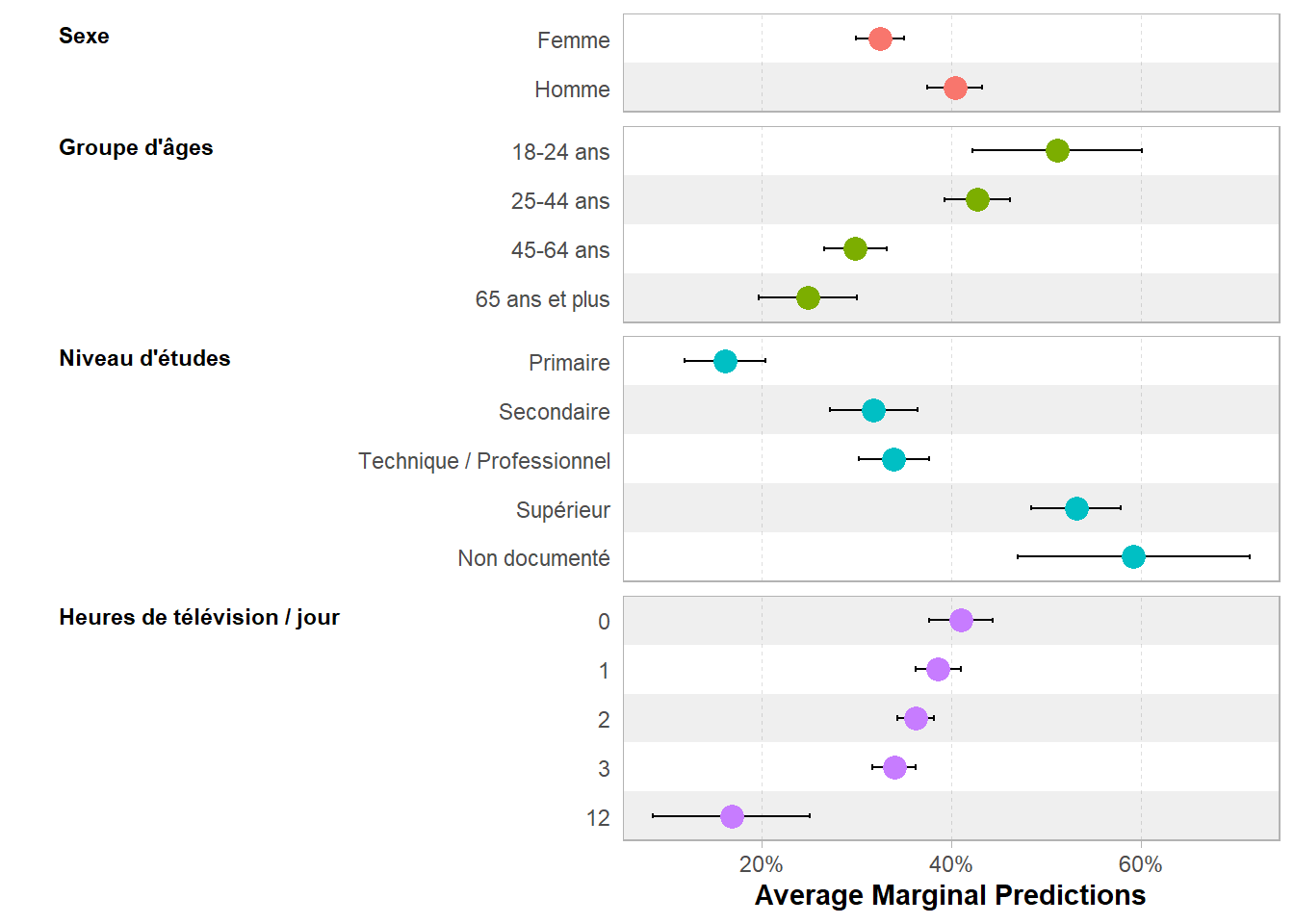
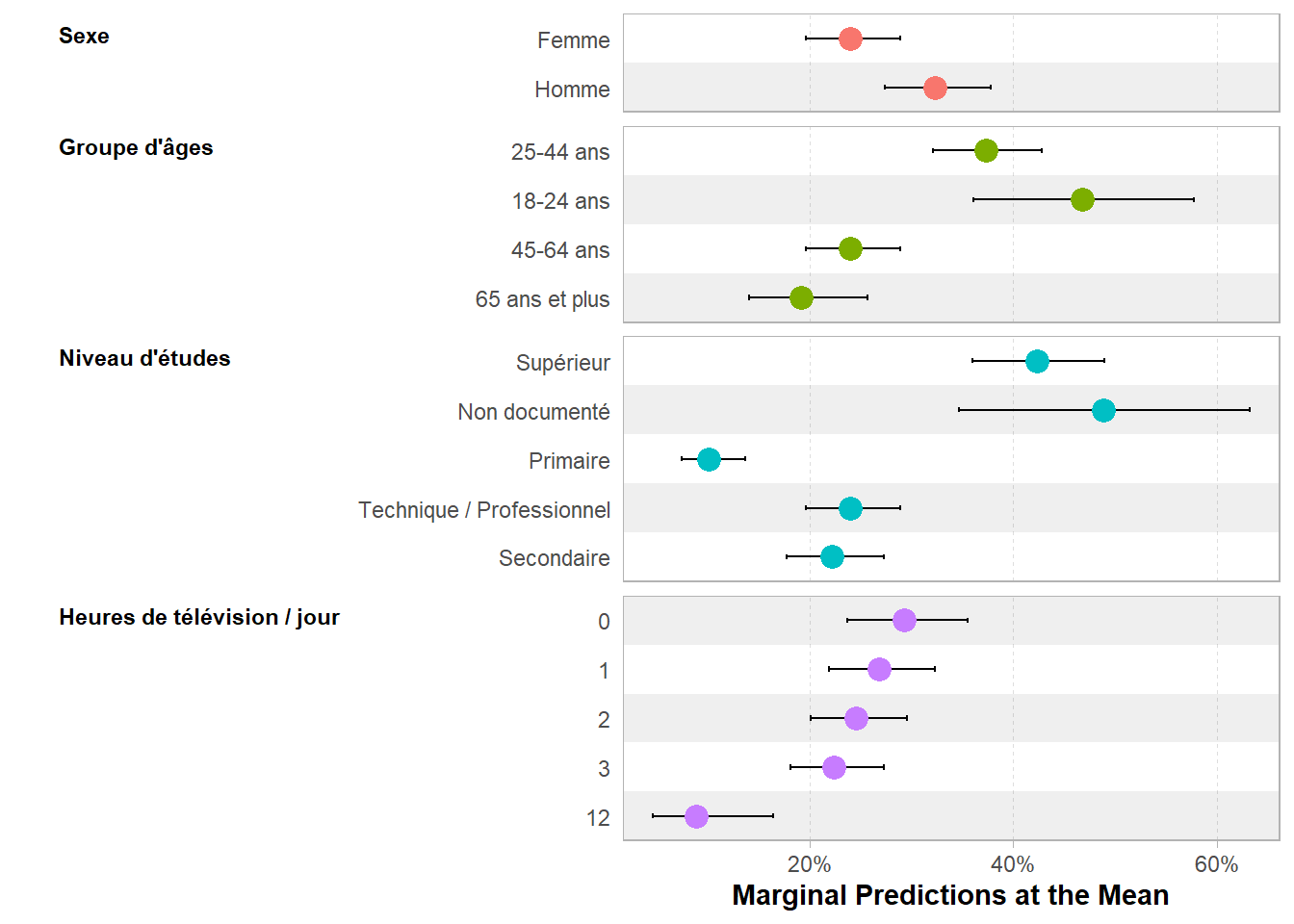
De même, on peut générer une représentation graphique :
Si l’on souhaite utiliser ggstats::ggcoef_model(), on peut directement indiquer newdata = "mean". Il faudra passer cette option via tidy_args qui prend une liste d’arguments à transmettre à tidy_fun.
mod |>
ggstats::ggcoef_model(
tidy_fun = broom.helpers::tidy_marginal_predictions,
tidy_args = list(newdata = "mean"),
show_p_values = FALSE,
signif_stars = FALSE,
significance = NULL,
vline = FALSE
) +
scale_x_continuous(labels = scales::label_percent())
24.3.2.2 avec {effects}
Le package effects3 adopte une approche un peu différente pour définir un individu moyen
.
3 Malgré son nom, le package effects ne calcule pas des effets marginaux mais des prédictions marginales, selon la terminologie retenue au début de ce document.
Calculons les prédictions marginales à la moyenne avec la fonction effects::Effect().
On le voit, les résultats sont là encore assez proches mais différents. Regardons de plus près les données utilisées pour les prédictions.
(Intercept) sexeHomme groupe_ages25-44 ans groupe_ages45-64 ans
1 1 0 0.3533835 0.3719298
2 1 1 0.3533835 0.3719298
groupe_ages65 ans et plus etudesSecondaire etudesTechnique / Professionnel
1 0.1904762 0.193985 0.2962406
2 0.1904762 0.193985 0.2962406
etudesSupérieur etudesNon documenté heures.tv
1 0.2205514 0.05614035 2.246566
2 0.2205514 0.05614035 2.246566
attr(,"assign")
[1] 0 1 2 2 2 3 3 3 3 4
attr(,"contrasts")
attr(,"contrasts")$sexe
[1] "contr.treatment"
attr(,"contrasts")$groupe_ages
[1] "contr.treatment"
attr(,"contrasts")$etudes
[1] "contr.treatment"Pour les variables continues, effects utilise la moyenne observée de la variable, comme précédemment avec marginaleffects. Par contre, pour les variables catégorielles, ce n’est pas le mode qui est utilisé, mais l’ensemble des modalités, pondérées selon leur proportion observée dans l’échantillon. Cette approche a l’avantage de moyenniser
également les variables catégorielles, même si les individus pour lesquels une prédiction est réalisée sont complètement fictifs.
On peut utiliser broom.helpers::tidy_all_effects() pour générer un tableau de prédictions marginales avec effects.
mod |>
tbl_regression(
tidy_fun = broom.helpers::tidy_all_effects,
estimate_fun = scales::label_percent(accuracy = 0.1)
) |>
bold_labels()Caractéristique |
Prédictions Marginales à la Moyenne |
95% IC 1 |
|---|---|---|
| Sexe | ||
| Femme | 28.7% | 25.8% – 31.8% |
| Homme | 37.9% | 34.4% – 41.6% |
| Groupe d'âges | ||
| 18-24 ans | 51.2% | 41.0% – 61.3% |
| 25-44 ans | 41.5% | 37.4% – 45.7% |
| 45-64 ans | 27.3% | 23.9% – 30.9% |
| 65 ans et plus | 22.0% | 17.4% – 27.5% |
| Niveau d'études | ||
| Primaire | 14.9% | 11.3% – 19.3% |
| Secondaire | 30.7% | 26.2% – 35.7% |
| Technique / Professionnel | 32.9% | 29.1% – 37.0% |
| Supérieur | 53.4% | 48.3% – 58.4% |
| Non documenté | 59.9% | 46.6% – 71.8% |
| Heures de télévision / jour | ||
| 0 | 38.9% | 34.8% – 43.2% |
| 3 | 30.7% | 28.1% – 33.4% |
| 6 | 23.6% | 18.9% – 28.9% |
| 9 | 17.7% | 11.9% – 25.4% |
| 10 | 16.0% | 10.1% – 24.4% |
|
1
IC = intervalle de confiance |
||
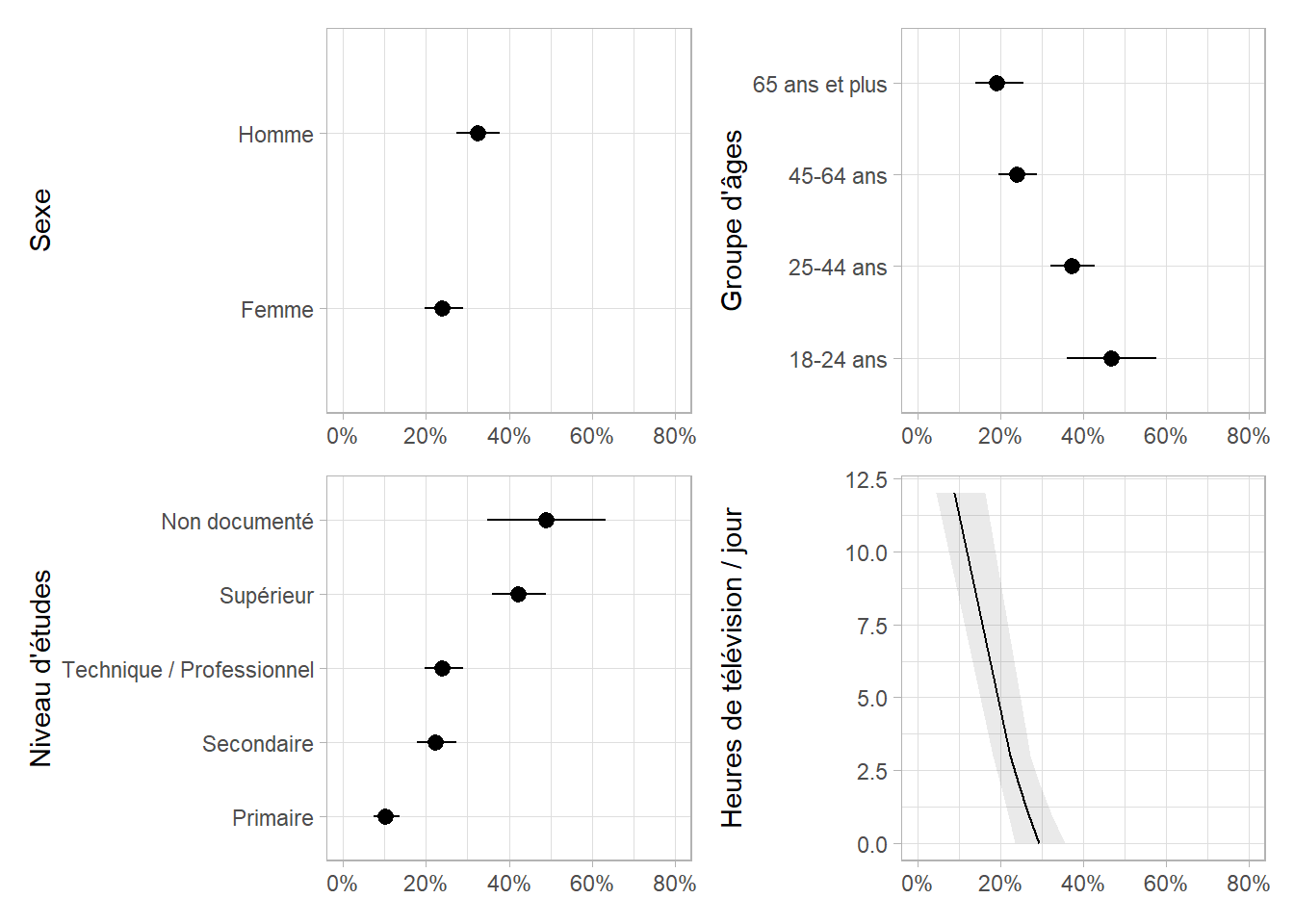
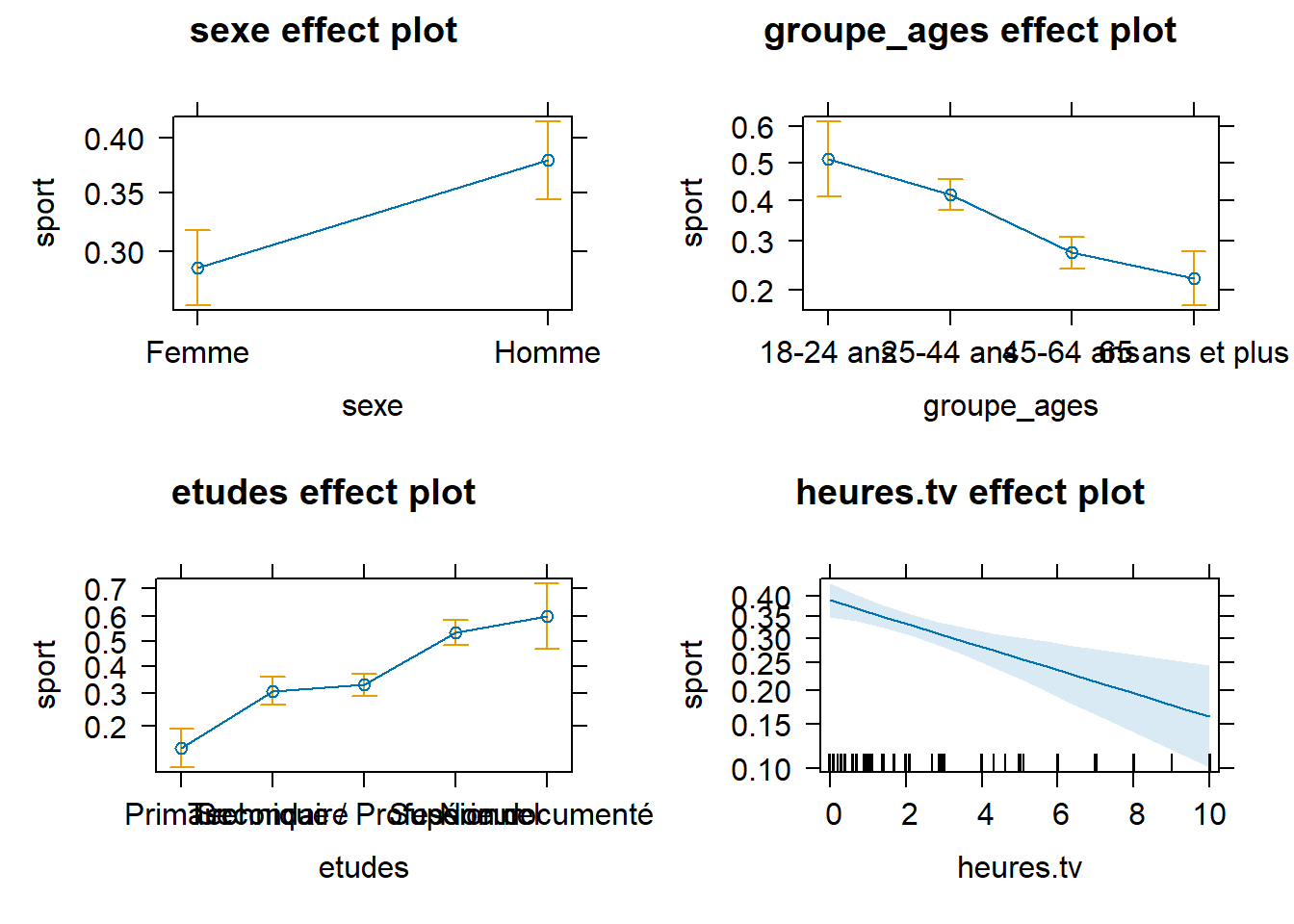
Pour une représentation graphique, nous pouvons utiliser les fonctions internes d’effects en appliquant plot() aux résultats de effects::allEffects() qui calcule les prédictions marginales de chaque variable.
On peut aussi utiliser ggstats::ggcoef_model()4.
4 De manière générale, ggstats::ggcoef_model() est compatible avec les mêmes tidy_fun que gtsummary::tbl_regression(), les deux fonctions utilisant en interne broom.helpers::tidy_plus_plus().
24.3.3 Variantes
Le package ggeffects propose une fonction ggeffects::ggpredict() qui calcule des prédictions marginales à la moyenne des variables continues et à la première modalité (utilisée comme référence) des variables catégorielles. On ne peut donc plus, au sens strict, parler de prédictions à la moyenne
. broom.helpers fournit une fonction tidy_ggpredict().
mod |>
tbl_regression(
tidy_fun = broom.helpers::tidy_ggpredict,
estimate_fun = scales::label_percent(accuracy = 0.1)
) |>
bold_labels()Data were 'prettified'. Consider using `terms="heures.tv [all]"` to get
smooth plots.Caractéristique |
Prédictions Marginales |
95% IC 1 |
|---|---|---|
| Sexe | ||
| Femme | 23.8% | 15.3% – 35.1% |
| Homme | 32.2% | 21.4% – 45.4% |
| Groupe d'âges | ||
| 18-24 ans | 23.8% | 15.3% – 35.1% |
| 25-44 ans | 17.5% | 12.7% – 23.5% |
| 45-64 ans | 10.1% | 7.3% – 13.7% |
| 65 ans et plus | 7.8% | 5.5% – 10.9% |
| Niveau d'études | ||
| Primaire | 23.8% | 15.3% – 35.1% |
| Secondaire | 44.2% | 33.0% – 56.1% |
| Technique / Professionnel | 46.8% | 36.1% – 57.8% |
| Supérieur | 67.2% | 56.2% – 76.6% |
| Non documenté | 72.8% | 62.8% – 80.9% |
| Heures de télévision / jour | ||
| 0 | 29.1% | 18.7% – 42.3% |
| 1 | 26.7% | 17.2% – 38.9% |
| 2 | 24.4% | 15.7% – 35.8% |
| 3 | 22.2% | 14.2% – 33.0% |
| 4 | 20.2% | 12.8% – 30.4% |
| 5 | 18.3% | 11.4% – 28.2% |
| 6 | 16.6% | 10.0% – 26.1% |
| 7 | 15.0% | 8.8% – 24.3% |
| 8 | 13.5% | 7.7% – 22.7% |
| 9 | 12.1% | 6.6% – 21.2% |
| 10 | 10.9% | 5.7% – 19.9% |
| 11 | 9.8% | 4.9% – 18.7% |
| 12 | 8.8% | 4.2% – 17.6% |
|
1
IC = intervalle de confiance |
||
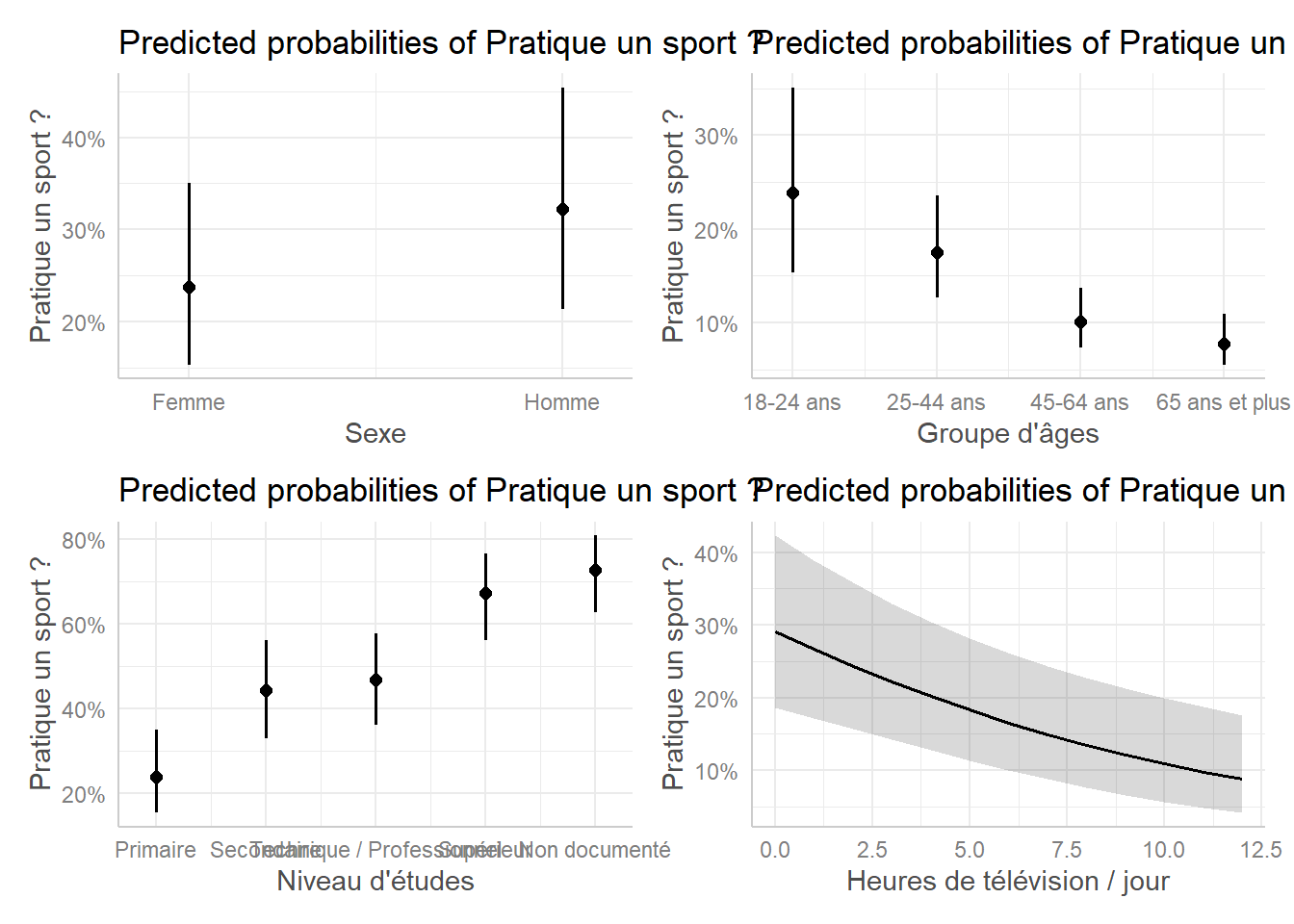
Pour une représentation graphique, on peut utiliser les fonctionnalités natives inclues dans le package ggeffects.
24.4 Contrastes marginaux
Maintenant que nous savons estimer des prédictions marginales, nous pouvons facilement calculer des contrastes marginaux, à savoir des différences entre prédictions marginales.
24.4.1 Contrastes marginaux moyens
Considérons tout d’abord la variable catégorielle sexe et calculons les prédictions marginales moyennes avec marginaleffects::predictions().
sexe Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
Femme 0.325 0.0130 25.0 <0.001 456.7 0.299 0.350
Homme 0.404 0.0147 27.5 <0.001 549.0 0.375 0.432
Columns: sexe, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high
Type: response Le contraste entre les hommes et les femmes est tout simplement la différence et les deux prédictions marginales.
La fonction marginaleffects::avg_comparisons() permet de réaliser directement ce calcul.
Term Contrast Estimate Std. Error z Pr(>|z|) S 2.5 %
sexe mean(Homme) - mean(Femme) 0.0788 0.0197 4 <0.001 14.0 0.0402
97.5 %
0.117
Columns: term, contrast, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted
Type: response
Astuce
Dans les faits, marginaleffects::avg_comparisons() a calculé la différence entre les hommes et les femmes pour chaque observation d’origine puis a réalisé la moyenne des différences. Mathématiquement, la moyenne des différences est équivalente à la différence des moyennes.
Les contrastes calculés ici ont été moyennés sur l’ensemble des valeurs observées. On parle donc de contrastes marginaux moyens (average marginal contrasts).
Par défaut, chaque modalité est contrastée avec la première modalité prise comme référence (voir exemple ci-dessous avec la variable groupe_ages.
Regardons maintenant une variable continue.
Term Contrast Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
heures.tv mean(+1) -0.0224 0.00606 -3.7 <0.001 12.2 -0.0343 -0.0105
Columns: term, contrast, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted
Type: response Par défaut, marginaleffects::avg_comparisons() calcule, pour chaque valeur observée de heures.tv, l’effet sur la probabilité de pratiquer un sport d’augmenter de 1 le nombre d’heures quotidiennes de télévision (plus précisément la différence des valeurs prédites pour la valeur observée plus 0,5 et la valeur observée moins 0,5).
On peut facilement obtenir la liste des contrastes marginaux pour l’ensemble des variables.
Term Contrast Estimate
etudes mean(Non documenté) - mean(Primaire) 0.4309
etudes mean(Secondaire) - mean(Primaire) 0.1568
etudes mean(Supérieur) - mean(Primaire) 0.3701
etudes mean(Technique / Professionnel) - mean(Primaire) 0.1781
groupe_ages mean(25-44 ans) - mean(18-24 ans) -0.0844
groupe_ages mean(45-64 ans) - mean(18-24 ans) -0.2127
groupe_ages mean(65 ans et plus) - mean(18-24 ans) -0.2631
heures.tv mean(+1) -0.0224
sexe mean(Homme) - mean(Femme) 0.0788
Std. Error z Pr(>|z|) S 2.5 % 97.5 %
0.06915 6.23 <0.001 31.0 0.2954 0.5665
0.03143 4.99 <0.001 20.6 0.0952 0.2184
0.03370 10.98 <0.001 90.8 0.3040 0.4361
0.02948 6.04 <0.001 29.3 0.1203 0.2359
0.04921 -1.71 0.0865 3.5 -0.1808 0.0121
0.05070 -4.20 <0.001 15.2 -0.3121 -0.1133
0.05558 -4.73 <0.001 18.8 -0.3720 -0.1541
0.00606 -3.70 <0.001 12.2 -0.0343 -0.0105
0.01970 4.00 <0.001 14.0 0.0402 0.1175
Columns: term, contrast, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted
Type: response Il est important de noter que le nom des colonnes n’est pas compatible avec les fonctions de broom.helpers et par extension avec gtsummary::tbl_regression() et ggstats::ggcoef_model(). On utilisera donc broom.helpers::tidy_marginal_contrasts()5 qui remets en forme le tableau de résultats dans un format compatible. On pourra ainsi produire un tableau propre des résultats6. Au sens strict, les contrastes obtenus s’expriment en points de pourcentage. Pour éviter toute mauvaise interprétation des résultats, on privilégiera la notation pp (points de pourcentage) plutôt que le symbole %.
5 Il existe également une fonction broom.helpers::tidy_avg_comparisons() mais on lui préférera broom.helpers::tidy_marginal_contrasts(). Pour un modèle sans interaction, les résultats sont identiques. Mais broom.helpers::tidy_marginal_contrasts() peut gérer des termes d’interactions, ce qui sera utile dans un prochain chapitre (cf. Chapitre 26).
6 Notez l’utilisation de style_positive = "plus" dans l’appel de scales::label_percent() pour ajouter un signe + devant les valeurs positives, afin de bien indiquer que l’on représente le résultat d’une différence.
mod |>
tbl_regression(
tidy_fun = broom.helpers::tidy_marginal_contrasts,
estimate_fun = scales::label_percent(
accuracy = 0.1,
style_positive = "plus",
suffix = " pp"
)
) |>
bold_labels()Caractéristique |
Contrastes Marginaux Moyens |
95% IC 1 |
p-valeur |
|---|---|---|---|
| Sexe | |||
| mean(Homme) - mean(Femme) | +7.9 pp | +4.0 pp – +11.7 pp | <0,001 |
| Groupe d'âges | |||
| mean(25-44 ans) - mean(18-24 ans) | -8.4 pp | -18.1 pp – +1.2 pp | 0,086 |
| mean(45-64 ans) - mean(18-24 ans) | -21.3 pp | -31.2 pp – -11.3 pp | <0,001 |
| mean(65 ans et plus) - mean(18-24 ans) | -26.3 pp | -37.2 pp – -15.4 pp | <0,001 |
| Niveau d'études | |||
| mean(Non documenté) - mean(Primaire) | +43.1 pp | +29.5 pp – +56.6 pp | <0,001 |
| mean(Secondaire) - mean(Primaire) | +15.7 pp | +9.5 pp – +21.8 pp | <0,001 |
| mean(Supérieur) - mean(Primaire) | +37.0 pp | +30.4 pp – +43.6 pp | <0,001 |
| mean(Technique / Professionnel) - mean(Primaire) | +17.8 pp | +12.0 pp – +23.6 pp | <0,001 |
| Heures de télévision / jour | |||
| mean(+1) | -2.2 pp | -3.4 pp – -1.1 pp | <0,001 |
|
1
IC = intervalle de confiance |
|||
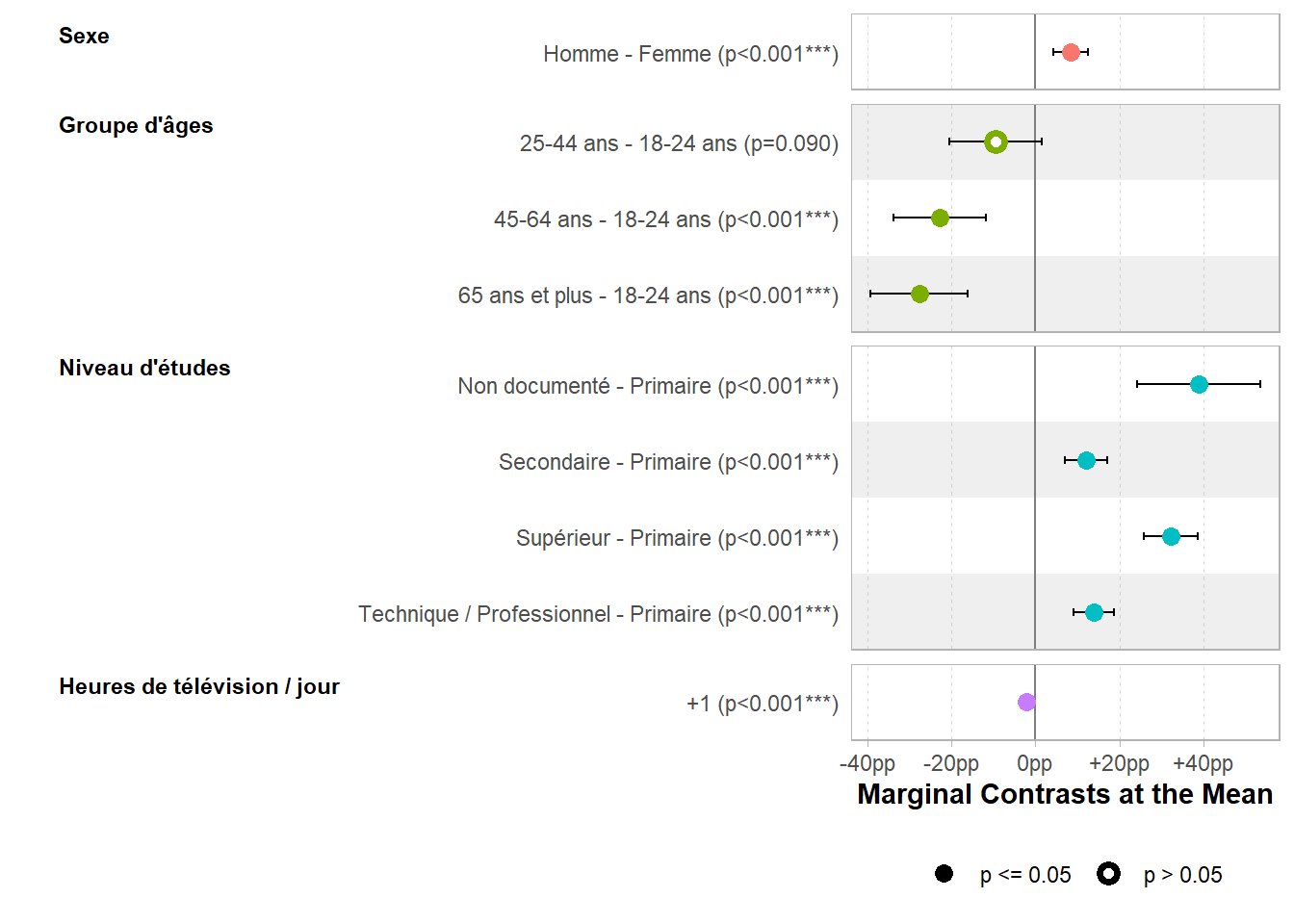
De même, on peut représenter les contrastes marginaux moyens avec ggstats::ggcoef_model().
ggstats::ggcoef_model(
mod,
tidy_fun = broom.helpers::tidy_marginal_contrasts
) +
ggplot2::scale_x_continuous(
labels = scales::label_percent(
style_positive = "plus",
suffix = "pp"
)
)
Astuce
Il est possible de personnaliser le type de contrastes calculés, variable par variable, avec l’option variables_list de broom.helpers::tidy_marginal_contrasts(). La syntaxe est un peu particulière : il faut transmettre une liste de listes.
mod |>
tbl_regression(
tidy_fun = broom.helpers::tidy_marginal_contrasts,
variables_list = list(
list(heures.tv = 2),
list(groupe_ages = "pairwise"),
list(etudes = "sequential")
),
estimate_fun = scales::label_percent(
accuracy = 0.1,
style_positive = "plus",
suffix = " pp"
)
) |>
bold_labels()Caractéristique |
Contrastes Marginaux Moyens |
95% IC 1 |
p-valeur |
|---|---|---|---|
| Heures de télévision / jour | |||
| mean(+2) | -4.4 pp | -6.7 pp – -2.1 pp | <0,001 |
| Groupe d'âges | |||
| mean(25-44 ans) - mean(18-24 ans) | -8.4 pp | -18.1 pp – +1.2 pp | 0,086 |
| mean(45-64 ans) - mean(18-24 ans) | -21.3 pp | -31.2 pp – -11.3 pp | <0,001 |
| mean(45-64 ans) - mean(25-44 ans) | -12.8 pp | -17.6 pp – -8.1 pp | <0,001 |
| mean(65 ans et plus) - mean(18-24 ans) | -26.3 pp | -37.2 pp – -15.4 pp | <0,001 |
| mean(65 ans et plus) - mean(25-44 ans) | -17.9 pp | -24.3 pp – -11.4 pp | <0,001 |
| mean(65 ans et plus) - mean(45-64 ans) | -5.0 pp | -11.0 pp – +0.9 pp | 0,10 |
| Niveau d'études | |||
| mean(Non documenté) - mean(Supérieur) | +6.1 pp | -7.0 pp – +19.2 pp | 0,4 |
| mean(Secondaire) - mean(Primaire) | +15.7 pp | +9.5 pp – +21.8 pp | <0,001 |
| mean(Supérieur) - mean(Technique / Professionnel) | +19.2 pp | +13.3 pp – +25.1 pp | <0,001 |
| mean(Technique / Professionnel) - mean(Secondaire) | +2.1 pp | -3.8 pp – +8.0 pp | 0,5 |
|
1
IC = intervalle de confiance |
|||
On peut obtenir le même résultat avec broom.helpers::tidy_avg_comparison() avec une syntaxe un peu plus simple (en passant une liste via variables au lieu d’une liste de listes via variables_list).
mod |>
tbl_regression(
tidy_fun = broom.helpers::tidy_avg_comparisons,
variables = list(
heures.tv = 2,
groupe_ages = "pairwise",
etudes = "sequential"
),
estimate_fun = scales::label_percent(
accuracy = 0.1,
style_positive = "plus",
suffix = " pp"
)
) |>
bold_labels()Caractéristique |
Contrastes Marginaux Moyens |
95% IC 1 |
p-valeur |
|---|---|---|---|
| Niveau d'études | |||
| mean(Non documenté) - mean(Supérieur) | +6.1 pp | -7.0 pp – +19.2 pp | 0,4 |
| mean(Secondaire) - mean(Primaire) | +15.7 pp | +9.5 pp – +21.8 pp | <0,001 |
| mean(Supérieur) - mean(Technique / Professionnel) | +19.2 pp | +13.3 pp – +25.1 pp | <0,001 |
| mean(Technique / Professionnel) - mean(Secondaire) | +2.1 pp | -3.8 pp – +8.0 pp | 0,5 |
| Groupe d'âges | |||
| mean(25-44 ans) - mean(18-24 ans) | -8.4 pp | -18.1 pp – +1.2 pp | 0,086 |
| mean(45-64 ans) - mean(18-24 ans) | -21.3 pp | -31.2 pp – -11.3 pp | <0,001 |
| mean(45-64 ans) - mean(25-44 ans) | -12.8 pp | -17.6 pp – -8.1 pp | <0,001 |
| mean(65 ans et plus) - mean(18-24 ans) | -26.3 pp | -37.2 pp – -15.4 pp | <0,001 |
| mean(65 ans et plus) - mean(25-44 ans) | -17.9 pp | -24.3 pp – -11.4 pp | <0,001 |
| mean(65 ans et plus) - mean(45-64 ans) | -5.0 pp | -11.0 pp – +0.9 pp | 0,10 |
| Heures de télévision / jour | |||
| mean(+2) | -4.4 pp | -6.7 pp – -2.1 pp | <0,001 |
|
1
IC = intervalle de confiance |
|||
24.4.2 Contrastes marginaux à la moyenne
Comme précédemment, plutôt que de calculer les contrastes marginaux pour chaque individu observé avant de faire la moyenne des résultats, une approche alternative consiste à considérer un individu moyen
/ typique
et à calculer les contrastes marginaux pour cet individu. On parle alors de contrastes marginaux à la moyenne (marginal contrasts at the mean).
Avec marginaleffects, il suffit de spécifier newdata = "mean". Les variables continues seront fixées à leur moyenne et les variables catégorielles à leur mode (modalité la plus fréquente dans l’échantillon).
mod |>
tbl_regression(
tidy_fun = broom.helpers::tidy_marginal_contrasts,
newdata = "mean",
estimate_fun = scales::label_percent(
accuracy = 0.1,
style_positive = "plus",
suffix = " pp"
)
) |>
bold_labels()Caractéristique |
Contrastes Marginaux à la Moyenne |
95% IC 1 |
p-valeur |
|---|---|---|---|
| Sexe | |||
| mean(Homme) - mean(Femme) | +8.4 pp | +4.3 pp – +12.5 pp | <0,001 |
| Groupe d'âges | |||
| mean(25-44 ans) - mean(18-24 ans) | -9.5 pp | -20.5 pp – +1.5 pp | 0,090 |
| mean(45-64 ans) - mean(18-24 ans) | -22.9 pp | -33.8 pp – -11.9 pp | <0,001 |
| mean(65 ans et plus) - mean(18-24 ans) | -27.6 pp | -39.2 pp – -16.1 pp | <0,001 |
| Niveau d'études | |||
| mean(Non documenté) - mean(Primaire) | +38.8 pp | +24.1 pp – +53.5 pp | <0,001 |
| mean(Secondaire) - mean(Primaire) | +12.0 pp | +7.0 pp – +17.1 pp | <0,001 |
| mean(Supérieur) - mean(Primaire) | +32.2 pp | +25.7 pp – +38.7 pp | <0,001 |
| mean(Technique / Professionnel) - mean(Primaire) | +13.9 pp | +9.0 pp – +18.7 pp | <0,001 |
| Heures de télévision / jour | |||
| mean(+1) | -2.1 pp | -3.3 pp – -1.0 pp | <0,001 |
|
1
IC = intervalle de confiance |
|||
Pour la fonction ggstats::ggcoef_model(), on utilisera l’argument tidy_args pour transmettre l’option newdata = "mean".
24.5 Pentes marginales / Effets marginaux
Les effets marginaux, ou plus précisément les pentes marginales, sont similaires aux contrastes marginaux, avec un différence subtile. Pour une variable continue, les contrastes marginaux sont une différence entre deux prédictions tandis que les effets marginaux (marginal effects) ou pentes marginales (marginal slopes). Dis autrement, l’effet marginal d’un régresseur continu \(x\) est la pente / dérivée \({\partial y}/{\partial x}\) la fonction de prédiction \(y\), mesurée à des valeurs spécifiques de \(x\).
Les effets marginaux sont le plus souvent calculés selon l’échelle de l’outcome et représentent le changement attendu de l’outcome pour une augmentation du régresseur d’une unité.
Par définition, les effets marginaux ne sont pas définis pour les variables catégorielles. La plupart des fonctions rapportent, à la place, les contrastes marginaux pour ces variables catégorielles.
Comme pour les prédictions marginales et les contrastes marginaux, plusieurs approches existent (voir par exemple la vignette dédiée du package marginaleffects).
24.5.1 Pentes marginales moyennes / Effets marginaux moyens
Les effets marginaux moyens (average marginal effects) sont calculés en deux temps : (1) un effet marginal est calculé pour chaque individu observé dans le modèle ; (ii) puis la moyenne de ces effets individuels est calculée.
On aura tout simplement recours à la fonction marginaleffects::avg_slopes().
Term Contrast Estimate
etudes mean(Non documenté) - mean(Primaire) 0.4309
etudes mean(Secondaire) - mean(Primaire) 0.1568
etudes mean(Supérieur) - mean(Primaire) 0.3701
etudes mean(Technique / Professionnel) - mean(Primaire) 0.1781
groupe_ages mean(25-44 ans) - mean(18-24 ans) -0.0844
groupe_ages mean(45-64 ans) - mean(18-24 ans) -0.2127
groupe_ages mean(65 ans et plus) - mean(18-24 ans) -0.2631
heures.tv mean(dY/dX) -0.0227
sexe mean(Homme) - mean(Femme) 0.0788
Std. Error z Pr(>|z|) S 2.5 % 97.5 %
0.0691 6.23 <0.001 31.0 0.2954 0.5665
0.0314 4.99 <0.001 20.6 0.0952 0.2184
0.0337 10.98 <0.001 90.8 0.3040 0.4361
0.0295 6.04 <0.001 29.3 0.1203 0.2359
0.0492 -1.71 0.0865 3.5 -0.1808 0.0121
0.0507 -4.20 <0.001 15.2 -0.3121 -0.1133
0.0556 -4.73 <0.001 18.8 -0.3720 -0.1541
0.0062 -3.66 <0.001 11.9 -0.0348 -0.0105
0.0197 4.00 <0.001 14.0 0.0402 0.1175
Columns: term, contrast, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted
Type: response Pour un usage avec broom.helpers::tidy_plus_plus(), gtsummary::tbl_regression() ou ggstats::ggcoef_model(), on utilisera broom.helpers::tidy_avg_slopes().
mod |>
tbl_regression(
tidy_fun = broom.helpers::tidy_avg_slopes,
estimate_fun = scales::label_percent(
accuracy = 0.1,
style_positive = "plus",
suffix = " pp"
)
) |>
bold_labels()Caractéristique |
Effets Marginaux Moyens |
95% IC 1 |
p-valeur |
|---|---|---|---|
| Niveau d'études | |||
| mean(Non documenté) - mean(Primaire) | +43.1 pp | +29.5 pp – +56.6 pp | <0,001 |
| mean(Secondaire) - mean(Primaire) | +15.7 pp | +9.5 pp – +21.8 pp | <0,001 |
| mean(Supérieur) - mean(Primaire) | +37.0 pp | +30.4 pp – +43.6 pp | <0,001 |
| mean(Technique / Professionnel) - mean(Primaire) | +17.8 pp | +12.0 pp – +23.6 pp | <0,001 |
| Groupe d'âges | |||
| mean(25-44 ans) - mean(18-24 ans) | -8.4 pp | -18.1 pp – +1.2 pp | 0,086 |
| mean(45-64 ans) - mean(18-24 ans) | -21.3 pp | -31.2 pp – -11.3 pp | <0,001 |
| mean(65 ans et plus) - mean(18-24 ans) | -26.3 pp | -37.2 pp – -15.4 pp | <0,001 |
| Heures de télévision / jour | |||
| mean(dY/dX) | -2.3 pp | -3.5 pp – -1.1 pp | <0,001 |
| Sexe | |||
| mean(Homme) - mean(Femme) | +7.9 pp | +4.0 pp – +11.7 pp | <0,001 |
|
1
IC = intervalle de confiance |
|||
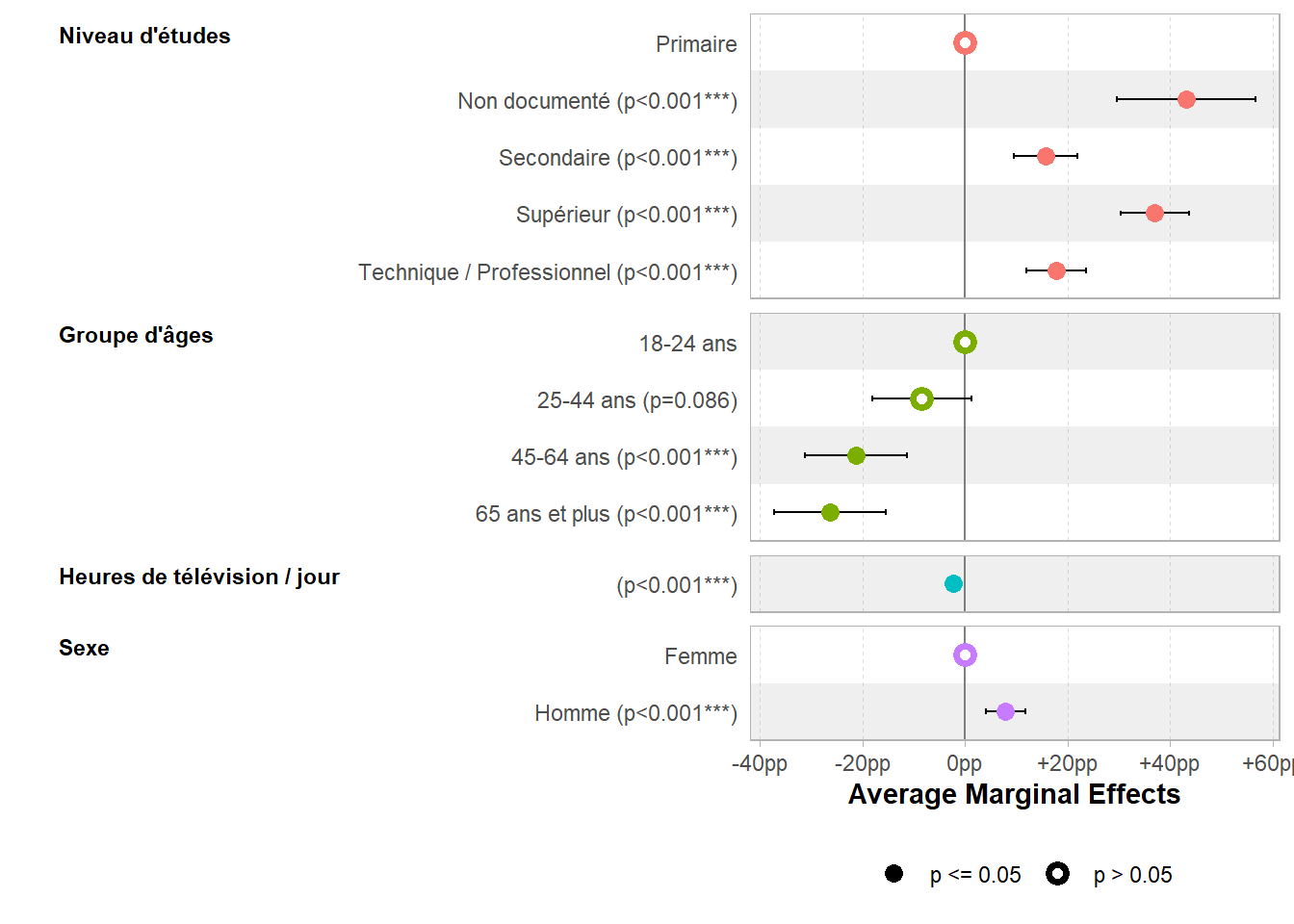
ggstats::ggcoef_model(
mod,
tidy_fun = broom.helpers::tidy_avg_slopes
) +
ggplot2::scale_x_continuous(
labels = scales::label_percent(
style_positive = "plus",
suffix = "pp"
)
)
Un résultat similaire peut être obtenu avec margins::margins(), le package margins s’inspirant de la commande Stata margins.
Warning: tidying a `margins` object was deprecated in broom 1.0.6.
ℹ margins was removed from CRAN in April 2024 and its tidiers are thus
untested.
! Please interpret output with caution.# A tibble: 9 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 etudesNon documenté 0.431 0.0691 6.23 4.60e-10
2 etudesSecondaire 0.157 0.0314 4.99 6.10e- 7
3 etudesSupérieur 0.370 0.0337 11.0 4.69e-28
4 etudesTechnique / Professionnel 0.178 0.0295 6.04 1.53e- 9
5 groupe_ages25-44 ans -0.0844 0.0492 -1.71 8.65e- 2
6 groupe_ages45-64 ans -0.213 0.0507 -4.20 2.73e- 5
7 groupe_ages65 ans et plus -0.263 0.0556 -4.73 2.21e- 6
8 heures.tv -0.0227 0.00620 -3.66 2.56e- 4
9 sexeHomme 0.0788 0.0197 4.00 6.26e- 5For broom.helpers, gtsummary or ggstats, use broom.helpers::tidy_margins().
mod |>
tbl_regression(
tidy_fun = broom.helpers::tidy_margins,
estimate_fun = scales::label_percent(
accuracy = 0.1,
style_positive = "plus",
suffix = " pp"
)
) |>
bold_labels()Caractéristique |
Effets Marginaux Moyens |
95% IC 1 |
p-valeur |
|---|---|---|---|
| Niveau d'études | |||
| Primaire | — | — | |
| Non documenté | +43.1 pp | +29.5 pp – +56.6 pp | <0,001 |
| Secondaire | +15.7 pp | +9.5 pp – +21.8 pp | <0,001 |
| Supérieur | +37.0 pp | +30.4 pp – +43.6 pp | <0,001 |
| Technique / Professionnel | +17.8 pp | +12.0 pp – +23.6 pp | <0,001 |
| Groupe d'âges | |||
| 18-24 ans | — | — | |
| 25-44 ans | -8.4 pp | -18.1 pp – +1.2 pp | 0,086 |
| 45-64 ans | -21.3 pp | -31.2 pp – -11.3 pp | <0,001 |
| 65 ans et plus | -26.3 pp | -37.2 pp – -15.4 pp | <0,001 |
| Heures de télévision / jour | -2.3 pp | -3.5 pp – -1.1 pp | <0,001 |
| Sexe | |||
| Femme | — | — | |
| Homme | +7.9 pp | +4.0 pp – +11.7 pp | <0,001 |
|
1
IC = intervalle de confiance |
|||
24.5.2 Pentes marginales à la moyenne / Effets marginaux à la moyenne
Pour les effets marginaux à la moyenne (marginal effects at the mean), simplement indiquer newdata = "mean" à broom.helpers::tidy_marginaleffects().
24.6 Lectures complémentaires (en anglais)
-
Documentation of the
marginaleffectspackage par Vincent Arel-Bundock - Marginalia: A guide to figuring out what the heck marginal effects, marginal slopes, average marginal effects, marginal effects at the mean, and all these other marginal things are par Andrew Heiss
- Introduction to Adjusted Predictions and Marginal Effects in R par Daniel Lüdecke
- An Introduction to
margins - Marginal effects / slopes, contrasts, means and predictions with broom.helpers
- The Marginal Effects Zoo par Vincent Arel-Bundock
24.7 webin-R
La régression logistique est présentée sur YouTube dans le webin-R #24 (Prédictions, contrastes & effets marginaux).