Call:
lm(formula = Petal.Width ~ Petal.Length, data = iris)
Coefficients:
(Intercept) Petal.Length
-0.3631 0.4158 21 Régression linéaire
Un modèle de régression linéaire est un modèle de régression qui cherche à établir une relation linéaire entre une variable continue, dite expliquée, et une ou plusieurs variables, dites explicatives.
21.1 Modèle à une seule variable explicative continue
Nous avons déjà abordé très rapidement la régression linéaire dans le chapitre sur la statistique bivariée (cf. Section 19.3).
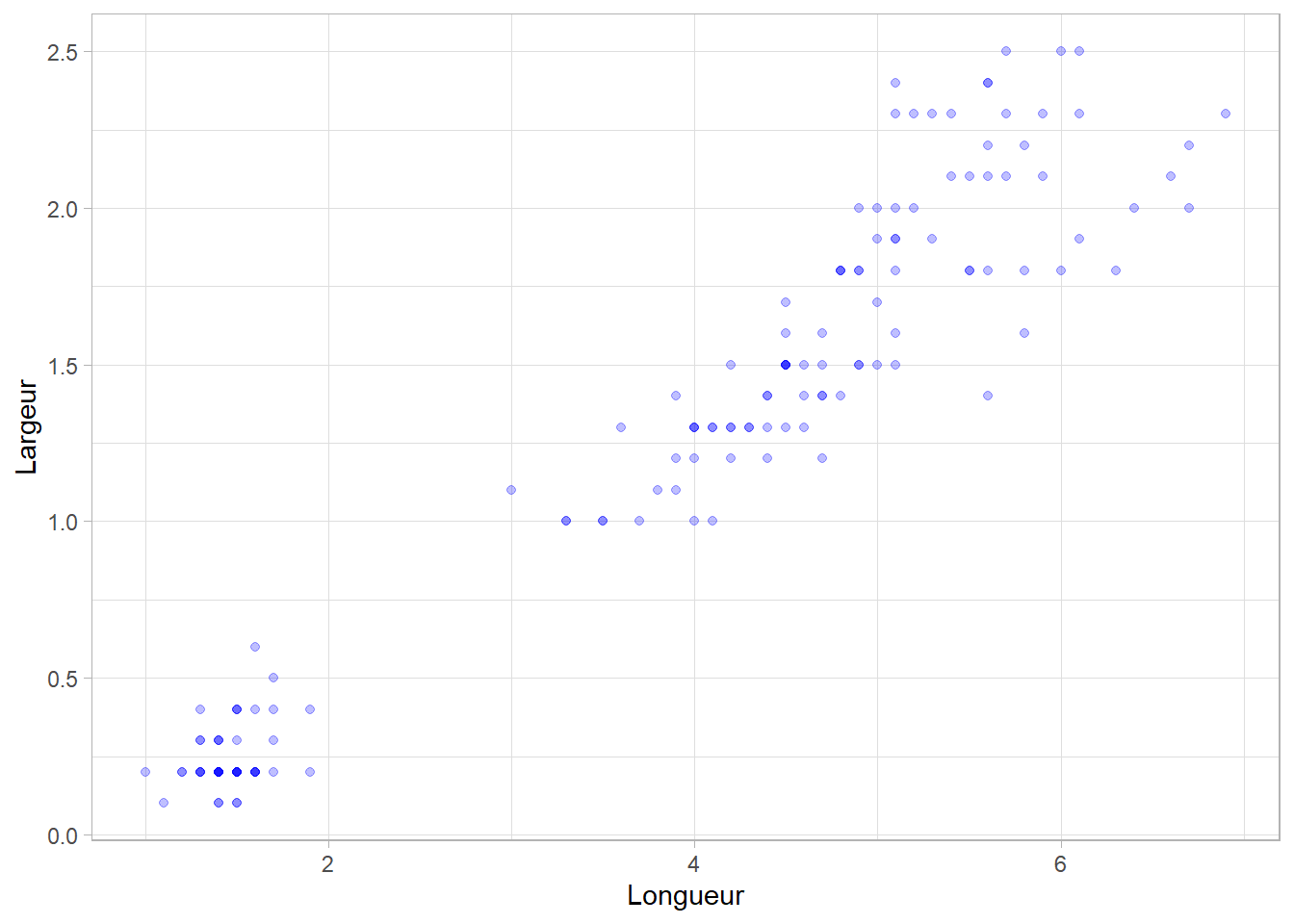
Reprenons le même exemple à partir du jeu de données iris qui comporte les caractéristiques de 150 fleurs de trois espèces différentes d’iris. Nous cherchons dans un premier temps à explorer la relation entre la largeur (Petal.Width) et la longueur des pétales (Petal.Length). Représentons cette relation sous la forme d’un nuage de points.
library(tidyverse)
ggplot(iris) +
aes(x = Petal.Length, y = Petal.Width) +
geom_point(colour = "blue", alpha = .25) +
labs(x = "Longueur", y = "Largeur") +
theme_light()
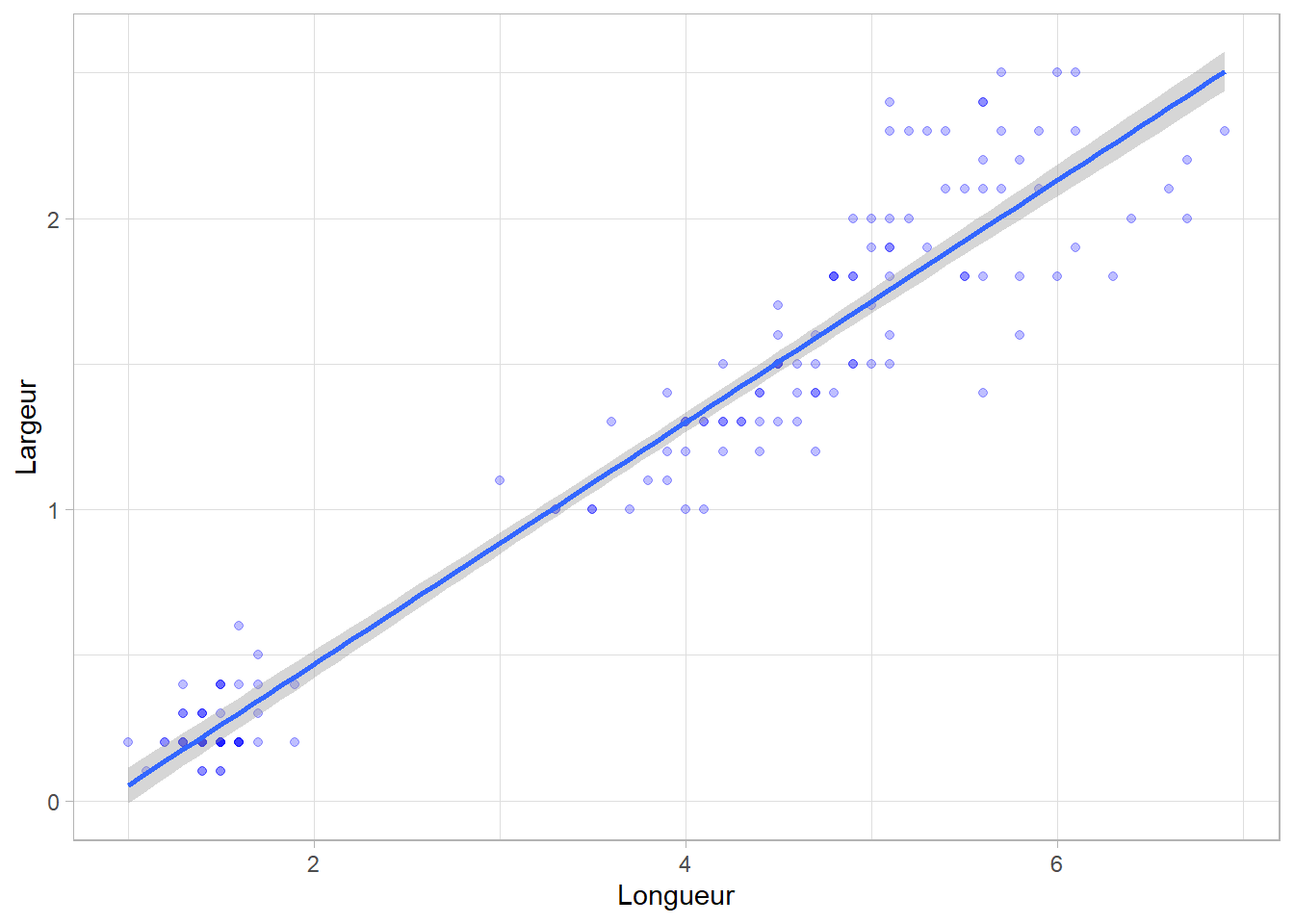
Il semble bien qu’il y a une relation linéaire entre ces deux variables, c’est-à-dire que la relation entre ces deux variables peut être représentée sous la forme d’une droite. Pour cela, on va rechercher la droite telle que la distance entre les points observés et la droite soit la plus petite possible. Cette droite peut être représentée graphique avec ggplot2::geom_smooth() et l’option method = "lm" :
ggplot(iris) +
aes(x = Petal.Length, y = Petal.Width) +
geom_point(colour = "blue", alpha = .25) +
geom_smooth(method = "lm") +
labs(x = "Longueur", y = "Largeur") +
theme_light()
La fonction de base pour calculer une régression linéaire est la fonction stats::m(). On doit en premier lieu spécifier le modèle à l’aide d’une formule : on indique la variable à expliquer dans la partie gauche de la formule et la variable explicative dans la partie droite, les deux parties étant séparées par un tilde1 (~).
1 Avec un clavier français, sous Windows, le caractère tilde s’obtient en pressant simultanément les touches Alt Gr et 7.
Dans le cas présent, la variable Petal.Width fait office de variable à expliquer et Petal.Length de variable explicative. Le modèle s’écrit donc Petal.Width ~ Petal.Length.
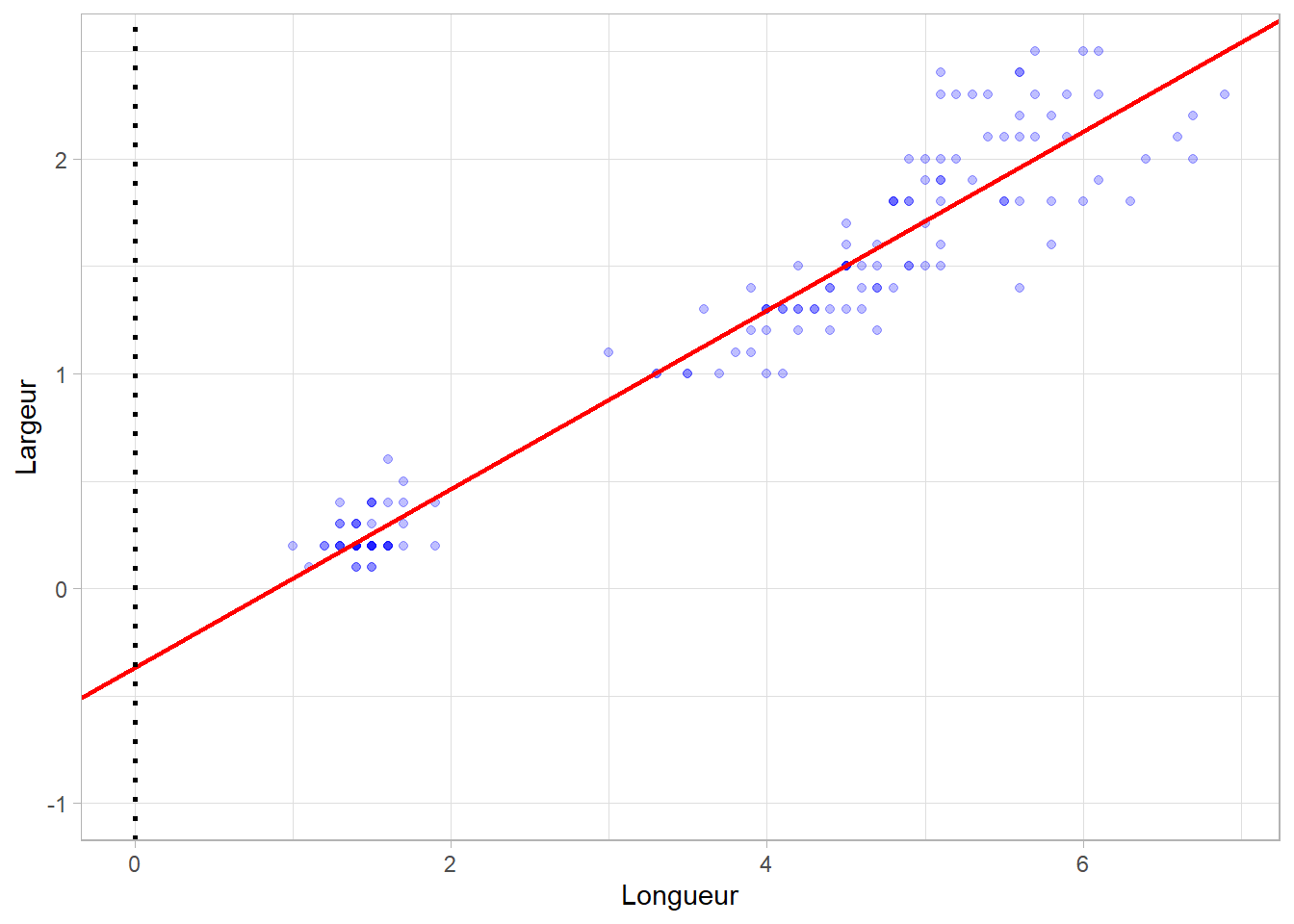
Le résultat comporte deux coefficients. Le premier, d’une valeur de \(0,4158\), est associé à la variable Petal.Length et indique la pente de la courbe (on parle de slope en anglais). Le second, d’une valeur de \(-0,3631\), représente l’ordonnée à l’origine (intercept en anglais), c’est-à-dire la valeur estimée de Petal.Width lorsque Petal.Length vaut 0. Nous pouvons rendre cela plus visible en élargissant notre graphique.
ggplot(iris) +
aes(x = Petal.Length, y = Petal.Width) +
geom_point(colour = "blue", alpha = .25) +
geom_abline(
intercept = mod$coefficients[1],
slope = mod$coefficients[2],
linewidth = 1,
colour = "red"
) +
geom_vline(xintercept = 0, linewidth = 1, linetype = "dotted") +
labs(x = "Longueur", y = "Largeur") +
expand_limits(x = 0, y = -1) +
theme_light()
Le modèle linéaire calculé estime donc que le relation entre nos deux variables peut s’écrire sous la forme suivante :
\[ Petal.Width = 0,4158 \cdot Petal.Length - 0,3631 \]
Le package gtsummary fournit gtsummary::tbl_regression(), une fonction bien pratique pour produire un tableau propre avec les coefficients du modèle, leur intervalle de confiance à 95% et leur p-valeurs2. On précisera intercept = TRUE pour forcer l’affichage de l’intercept qui est masqué par défaut.
2 Si l’on a besoin de ces informations sous la forme d’un tableau de données classique, on pourra se référer à broom.helpers::tidy_plus_plus(), utilisée de manière sous-jacente par gtsummary::tbl_regression(), ainsi qu’à la méthode broom::tidy(). Ces fonctions sont génériques et peut être utilisées avec une très grande variété de modèles.
Characteristic |
Beta |
95% CI 1 |
p-value |
|---|---|---|---|
| (Intercept) | -0.36 | -0.44, -0.28 | <0.001 |
| Petal.Length | 0.42 | 0.40, 0.43 | <0.001 |
|
1
CI = Confidence Interval |
|||
Les p-valeurs calculées nous indique si le coefficient est statistiquement différent de 0. En effet, pour la variable explicative, cela nous indique si la relation est statistiquement significative. Le signe du coefficient (positif ou négatif) nous indique le sens de la relation.
Astuce
Dans certains cas, si l’on suppose que la relation entre les deux variables est proportionnelle, on peut souhaiter calculer un modèle sans intercept. Par défaut, R ajoute un intercept à ses modèles. Pour forcer le calcul d’un modèle sans intercept, on ajoutera - 1 à la formule définissant le modèle.
21.2 Modèle à une seule variable explicative catégorielle
Si dans un modèle linéaire la variable à expliquer est nécessairement continue, il est possible de définir une variable explicative catégorielle. Prenons la variable Species.
pos variable label col_type missing values
5 Species — fct 0 setosa
versicolor
virginica Il s’agit d’un facteur à trois modalités. Par défaut, la première valeur du facteur (ici setosa) va servir de modalité de référence.
Call:
lm(formula = Petal.Width ~ Species, data = iris)
Coefficients:
(Intercept) Speciesversicolor Speciesvirginica
0.246 1.080 1.780 Characteristic |
Beta |
95% CI 1 |
p-value |
|---|---|---|---|
| (Intercept) | 0.25 | 0.19, 0.30 | <0.001 |
| Species | |||
| setosa | — | — | |
| versicolor | 1.1 | 1.0, 1.2 | <0.001 |
| virginica | 1.8 | 1.7, 1.9 | <0.001 |
|
1
CI = Confidence Interval |
|||
Dans ce cas de figure, l’intercept représente la situation à la référence, donc pour l’espèce setosa.
Calculons les moyennes par espèce :
# A tibble: 3 × 2
Species `mean(Petal.Width)`
<fct> <dbl>
1 setosa 0.246
2 versicolor 1.33
3 virginica 2.03 Comme on le voit, l’intercept nous indique donc la moyenne observée pour l’espèce de référence (\(0,246\)).
Le coefficient associé à versicolor correspond à la différence par rapport à la référence (ici \(+1,080\)). Comme vous pouvez le constater, il s’agit de la différence entre la moyenne observée pour versicolor (\(1,326\)) et celle de la référence setosa (\(0,246\)) : \(1,326-0,246=1,080\).
Ce coefficient est significativement différent de 0 (p<0,001), indiquant que la largeur des pétales diffère significativement entre les deux espèces.
Astuce
Lorsque l’on calcule le même modèle sans intercept, les coefficients s’interprètent un différemment :
Call:
lm(formula = Petal.Width ~ Species - 1, data = iris)
Coefficients:
Speciessetosa Speciesversicolor Speciesvirginica
0.246 1.326 2.026 En l’absence d’intercept, trois coefficients sont calculés et il n’y a plus ici de modalité de référence. Chaque coefficient représente donc la moyenne observée pour chaque modalité.
On appelle contrastes les différents manières de coder des variables catégorielles dans un modèle. Nous y reviendrons plus en détail dans un chapitre dédié (cf. Chapitre 25).
21.3 Modèle à plusieurs variables explicatives
Un des intérêts de la régression linéaire est de pouvoir estimer un modèle multivariable, c’est-à-dire avec plusieurs variables explicatives.
Pour cela, on listera les différentes variables explicatives dans la partie droite de la formule, séparées par le symbole +.
Call:
lm(formula = Petal.Width ~ Petal.Length + Sepal.Width + Sepal.Length +
Species, data = iris)
Coefficients:
(Intercept) Petal.Length Sepal.Width Sepal.Length
-0.47314 0.24220 0.24220 -0.09293
Speciesversicolor Speciesvirginica
0.64811 1.04637
Note
Dans la littérature, on trouve fréquemment utilisée à tort l’expression de modèle multivarié en lieu et place de modèle multivariable. Ces dernières années, de nombreux auteurs ont poussé à une clarification de la terminologie et à une distinction entre un modèle multivarié et un modèle multivariable.
La régression c’est l’analyse la relation d’un outcome (variable à expliquer) par rapport à une ou plusieurs variables prédictives (variables explicatives).
Un modèle peut être simple ou univariable s’il ne comporte qu’une seule variable prédictive. Par contre, s’il comporte plusieurs variables prédictives, on parlera d’une régression multiple ou multivariable (multiple ou multivariable en anglais).
Si la variable à expliquer (outcome) est répétée, c’est-à-dire que l’on a plusieurs observations pour un même individu statistique, par exemple dans le cadre d’une étude longitudinale, on parlera alors d’une régression multivariées (multivariate en anglais). Il peut alors s’agir d’une régression simple multivariée ou bien d’une régression multivariable multivariée.
Par ailleurs, il ne faut pas confondre l’emploi des adjectifs univarié et bivarié appliqué aux termes statistiques ou analyses. L’analyse univariée ou la statistique univariée correspondent à l’analyse d’une seule variable (cf. Chapitre 18) tandis que la statistique bivariée correspond à l’analyse simultanée de deux variables (cf. Chapitre 19). Or, une régression simple ou univariable peut être utilisée dans le cadre d’une analyse bivariée.
Characteristic |
Beta |
95% CI 1 |
p-value |
|---|---|---|---|
| (Intercept) | -0.47 | -0.82, -0.12 | 0.008 |
| Petal.Length | 0.24 | 0.15, 0.34 | <0.001 |
| Sepal.Width | 0.24 | 0.15, 0.34 | <0.001 |
| Sepal.Length | -0.09 | -0.18, 0.00 | 0.039 |
| Species | |||
| setosa | — | — | |
| versicolor | 0.65 | 0.40, 0.89 | <0.001 |
| virginica | 1.0 | 0.72, 1.4 | <0.001 |
|
1
CI = Confidence Interval |
|||
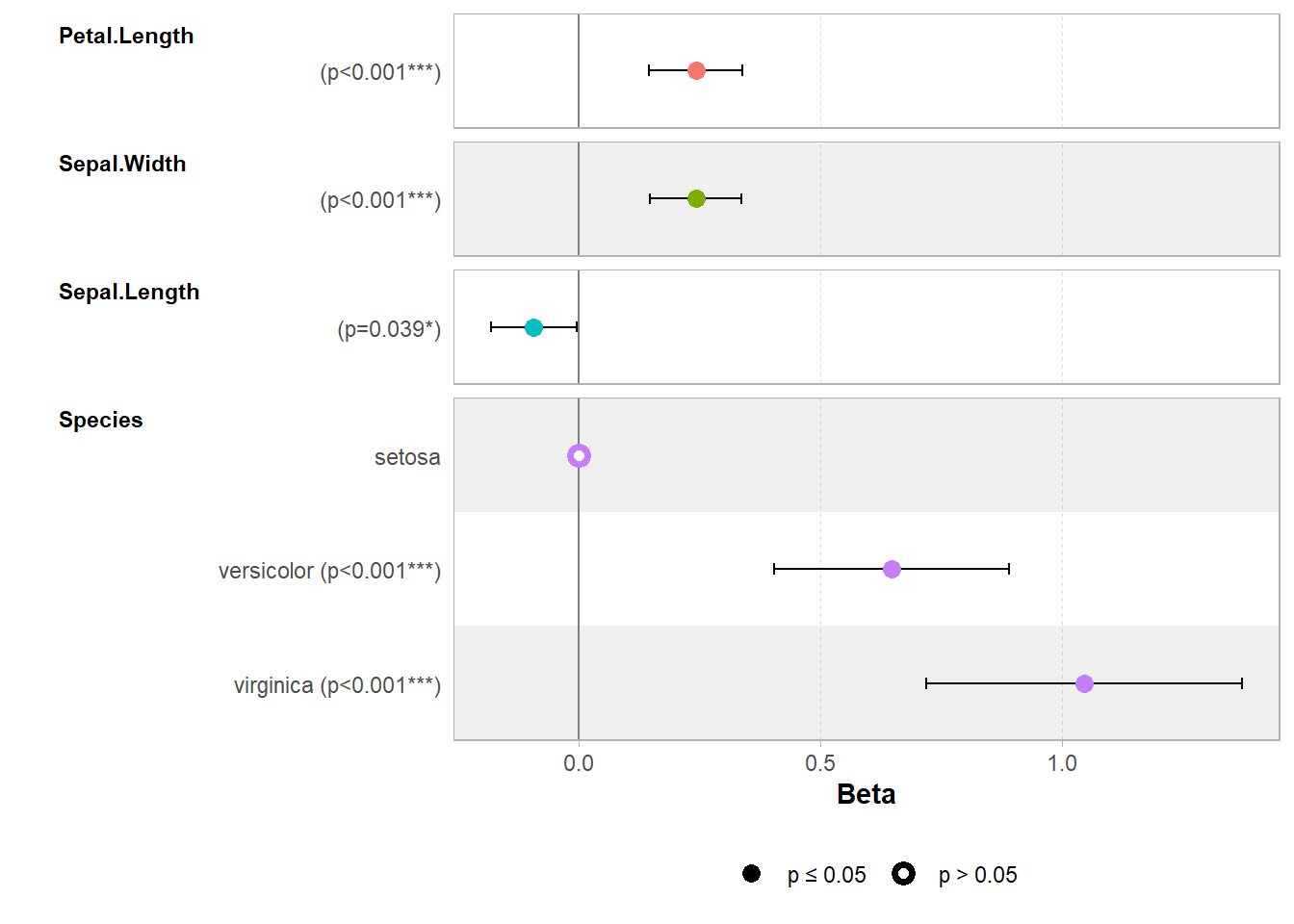
Ce type de modèle permet d’estimer l’effet de chaque variable explicative, toutes choses égales par ailleurs
. Dans le cas présent, on s’aperçoit que la largeur des pétales diffère significativement selon les espèces, est fortement corrélée positivement à la longueur du pétale et la largeur du sépale et qu’il y a, lorsque l’on ajuste sur l’ensemble des autres variables, une relation négative (faiblement significative) avec la longueur du sépale.
Lorsque le nombre de coefficients est élevé, une représentation graphique est souvent plus facile à lire qu’un tableau. On parle alors de graphique en forêt ou forest plot en anglais. Rien de plus facile ! Il suffit d’avoir recours à ggstats::ggcoef_model().
