43 Régression logistique multinomiale
La régression logistique multinomiale est une extension de la régression logistique binaire (cf. Chapitre 22) aux variables qualitatives à trois modalités ou plus. Dans ce cas de figure, chaque modalité de la variable d’intérêt sera comparée à une modalité de référence. Les odds ratio seront donc exprimés par rapport à cette dernière.
43.1 Données d’illustration
Pour illustrer la régression logistique multinomiale, nous allons reprendre le jeu de données hdv2003 du package questionr et portant sur l’enquête histoires de vie 2003 de l’Insee.
Nous allons considérer comme variable d’intérêt la variable trav.satisf, à savoir la satisfaction ou l’insatisfaction au travail.
# A tibble: 4 × 4
trav.satisf n N prop
<fct> <int> <int> <dbl>
1 Satisfaction 480 2000 24
2 Insatisfaction 117 2000 5.85
3 Equilibre 451 2000 22.6
4 <NA> 952 2000 47.6 Nous allons choisir comme modalité de référence la position intermédiaire, à savoir l’« équilibre », que nous allons donc définir comme la première modalité du facteur.
Nous allons aussi en profiter pour raccourcir les étiquettes de la variable trav.imp :
Enfin, procédons à quelques recodages additionnels :
d <- d |>
mutate(
sexe = sexe |> fct_relevel("Femme"),
groupe_ages = age |>
cut(
c(18, 25, 45, 99),
right = FALSE,
include.lowest = TRUE,
labels = c("18-24 ans", "25-44 ans",
"45 et plus")
),
etudes = nivetud |>
fct_recode(
"Primaire" = "N'a jamais fait d'etudes",
"Primaire" = "A arrete ses etudes, avant la derniere annee d'etudes primaires",
"Primaire" = "Derniere annee d'etudes primaires",
"Secondaire" = "1er cycle",
"Secondaire" = "2eme cycle",
"Technique / Professionnel" = "Enseignement technique ou professionnel court",
"Technique / Professionnel" = "Enseignement technique ou professionnel long",
"Supérieur" = "Enseignement superieur y compris technique superieur"
) |>
fct_na_value_to_level("Non documenté")
) |>
set_variable_labels(
trav.satisf = "Satisfaction dans le travail",
sexe = "Sexe",
groupe_ages = "Groupe d'âges",
etudes = "Niveau d'études",
trav.imp = "Importance accordée au travail"
)43.2 Calcul du modèle multinomial
Pour calculer un modèle logistique multinomial, nous allons utiliser la fonction nnet::multinom() de l’extension nnet1. La syntaxe de nnet::multinom() est similaire à celle de glm(), le paramètre family en moins.
1 Il existe plusieurs alternatives possibles : la fonction VGAM::vglm() avec family = VGAM::multinomial ou encore mlogit::mlogit(). Ces deux fonctions sont un peu plus complexes à mettre en œuvre. On se référera à la documentation de chaque package. Le support des modèles mlogit() et vglm() est aussi plus limité dans d’autres packages tels que broom.helpers, gtsummary, ggstats ou encore marginaleffects.
# weights: 36 (22 variable)
initial value 1151.345679
iter 10 value 977.985279
iter 20 value 971.187398
final value 971.113280
convergedComme pour la régression logistique binaire, il est possible de réaliser une sélection pas à pas descendante (cf. Chapitre 23) :
trying - sexe
trying - etudes
trying - groupe_ages
trying - trav.imp
trying - sexe
trying - etudes
trying - trav.imp
trying - etudes
trying - trav.imp 43.3 Affichage des résultats du modèle
Une des particularités de la régression logistique multinomiale est qu’elle produit une série de coefficients pour chaque modalité de la variable d’intérêt (sauf la modalité de référence). Ici, nous aurons donc une série de coefficients pour celles et ceux qui sont satisfaits au travail (comparés à la modalité Équilibre
) et une série de coefficients pour celles et ceux qui sont insatisfaits (comparés aux aussi à la modalité Équilibre
).
La fonction gtsummary::tbl_regression() peut gérer ce type de modèles, et va afficher les deux séries de coefficients l’une au-dessus de l’autre. Nous allons indiquer exponentiate = TRUE car, comme pour la régression logistique binaire, l’exponentielle des coefficients peut s’interpréter comme des odds ratios. Dans le cas présent, le tableau retourné est un tableau groupé
, c’est-à-dire que sa structure est légèrement différente, avec les coefficients groupés par niveau de la variable à expliquer. De fait, les fonctions comme gtsummary::bold_labels() ne fonctionneront pas forcément et il n’y pas de fonction native pour la mise en forme des étiquettes des groupes. On pourra alors avoir recours à la fonction guideR::style_grouped_tbl() de guideR, le package compagnon de guide-R. Attention : le tableau sera converti au format gt afin de mettre en forme les étiquettes des groupes. On appellera donc guideR::style_grouped_tbl() en tout dernier. En cas de conversion dans un autre format (data frame, flextable, …), on évitera donc cette fonction.
ℹ Multinomial models have a different underlying structure than the models
gtsummary was designed for.
• Functions designed to work with `tbl_regression()` objects may yield
unexpected results.| Caractéristique | OR | 95% IC | p-valeur |
|---|---|---|---|
| Satisfaction | |||
| Niveau d'études | |||
| Primaire | — | — | |
| Secondaire | 1,05 | 0,63 – 1,76 | 0,9 |
| Technique / Professionnel | 1,08 | 0,67 – 1,73 | 0,7 |
| Supérieur | 2,01 | 1,24 – 3,27 | 0,005 |
| Non documenté | 0,58 | 0,18 – 1,86 | 0,4 |
| Importance accordée au travail | |||
| Le plus | — | — | |
| Aussi | 1,29 | 0,56 – 2,98 | 0,5 |
| Moins | 0,84 | 0,37 – 1,88 | 0,7 |
| Peu | 0,55 | 0,18 – 1,64 | 0,3 |
| Insatisfaction | |||
| Niveau d'études | |||
| Primaire | — | — | |
| Secondaire | 0,91 | 0,41 – 1,99 | 0,8 |
| Technique / Professionnel | 1,09 | 0,54 – 2,19 | 0,8 |
| Supérieur | 1,08 | 0,51 – 2,29 | 0,8 |
| Non documenté | 0,96 | 0,18 – 4,97 | >0,9 |
| Importance accordée au travail | |||
| Le plus | — | — | |
| Aussi | 0,80 | 0,24 – 2,69 | 0,7 |
| Moins | 0,59 | 0,18 – 1,88 | 0,4 |
| Peu | 3,82 | 1,05 – 13,9 | 0,042 |
| Abréviations: IC = intervalle de confiance, OR = rapport de cotes | |||
L’odds ratio du niveau d’étude supérieur pour la modalité satisfaction est de 2,01, indiquant que les personnes ayant un niveau d’étude supérieur ont plus de chances d’être satisfait au travail que d’être à l’équilibre que les personnes de niveau primaire. Par contre, l’OR est de seulement 1,08 (et non significatif) pour la modalité Insatisfait indiquant que ces personnes n’ont ni plus ni moins de chance d’être insatisfaite que d’être à l’équilibre.
On notera au passage un message d’avertissement de gtsummary sur le fait que les modèles multinomiaux n’ont pas la même structure que d’autres modèles.
La fonction gtsummary::tbl_regression() affiche le tableau des coefficients dans un format long. Or, il est souvent plus lisible de présenter les coefficients dans un format large, avec les coefficients pour chaque modalité côte à côte.
Cela n’est pas possible nativement avec gtsummary mais on pourra éventuellement utiliser la fonction guideR::grouped_tbl_pivot_wider()2 fournie par guideR, le package compagnon de guide-R.
| Caractéristique |
Satisfaction
|
Insatisfaction
|
||||
|---|---|---|---|---|---|---|
| OR | 95% IC | p-valeur | OR | 95% IC | p-valeur | |
| Niveau d'études | ||||||
| Primaire | — | — | — | — | ||
| Secondaire | 1,05 | 0,63 – 1,76 | 0,9 | 0,91 | 0,41 – 1,99 | 0,8 |
| Technique / Professionnel | 1,08 | 0,67 – 1,73 | 0,7 | 1,09 | 0,54 – 2,19 | 0,8 |
| Supérieur | 2,01 | 1,24 – 3,27 | 0,005 | 1,08 | 0,51 – 2,29 | 0,8 |
| Non documenté | 0,58 | 0,18 – 1,86 | 0,4 | 0,96 | 0,18 – 4,97 | >0,9 |
| Importance accordée au travail | ||||||
| Le plus | — | — | — | — | ||
| Aussi | 1,29 | 0,56 – 2,98 | 0,5 | 0,80 | 0,24 – 2,69 | 0,7 |
| Moins | 0,84 | 0,37 – 1,88 | 0,7 | 0,59 | 0,18 – 1,88 | 0,4 |
| Peu | 0,55 | 0,18 – 1,64 | 0,3 | 3,82 | 1,05 – 13,9 | 0,042 |
| Abréviations: IC = intervalle de confiance, OR = rapport de cotes | ||||||
2 Il s’agit d’une adaptation de la fonction multinom_pivot_wider() proposée sur GitHub Gist.
Pour tester l’effet globale d’une variable dans le modèle, on aura directement recours à car::Anova().
Analysis of Deviance Table (Type II tests)
Response: trav.satisf
LR Chisq Df Pr(>Chisq)
etudes 24.211 8 0.002112 **
trav.imp 48.934 6 7.687e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Si l’on applique gtsummary::add_global_p() au résultat de gtsummary::tbl_regression(), les p-valeurs seront recopiées pour chaque série de coefficients.
| Caractéristique | OR | 95% IC | p-valeur |
|---|---|---|---|
| Satisfaction | |||
| Niveau d'études | 0,002 | ||
| Primaire | — | — | |
| Secondaire | 1,05 | 0,63 – 1,76 | |
| Technique / Professionnel | 1,08 | 0,67 – 1,73 | |
| Supérieur | 2,01 | 1,24 – 3,27 | |
| Non documenté | 0,58 | 0,18 – 1,86 | |
| Importance accordée au travail | <0,001 | ||
| Le plus | — | — | |
| Aussi | 1,29 | 0,56 – 2,98 | |
| Moins | 0,84 | 0,37 – 1,88 | |
| Peu | 0,55 | 0,18 – 1,64 | |
| Insatisfaction | |||
| Niveau d'études | 0,002 | ||
| Primaire | — | — | |
| Secondaire | 0,91 | 0,41 – 1,99 | |
| Technique / Professionnel | 1,09 | 0,54 – 2,19 | |
| Supérieur | 1,08 | 0,51 – 2,29 | |
| Non documenté | 0,96 | 0,18 – 4,97 | |
| Importance accordée au travail | <0,001 | ||
| Le plus | — | — | |
| Aussi | 0,80 | 0,24 – 2,69 | |
| Moins | 0,59 | 0,18 – 1,88 | |
| Peu | 3,82 | 1,05 – 13,9 | |
| Abréviations: IC = intervalle de confiance, OR = rapport de cotes | |||
Une astuce consiste à cacher toutes ces colonnes de p-valeurs, n’afficher que la dernière et changer son titre de colonne. Pour cela, on pourra profiter de la fonction guideR::multinom_add_global_p_pivot_wider().
| Caractéristique |
Satisfaction
|
Insatisfaction
|
Likelihood-ratio test
|
||
|---|---|---|---|---|---|
| OR | 95% IC | OR | 95% IC | p-valeur | |
| Niveau d'études | 0,002 | ||||
| Primaire | — | — | — | — | |
| Secondaire | 1,05 | 0,63 – 1,76 | 0,91 | 0,41 – 1,99 | |
| Technique / Professionnel | 1,08 | 0,67 – 1,73 | 1,09 | 0,54 – 2,19 | |
| Supérieur | 2,01 | 1,24 – 3,27 | 1,08 | 0,51 – 2,29 | |
| Non documenté | 0,58 | 0,18 – 1,86 | 0,96 | 0,18 – 4,97 | |
| Importance accordée au travail | <0,001 | ||||
| Le plus | — | — | — | — | |
| Aussi | 1,29 | 0,56 – 2,98 | 0,80 | 0,24 – 2,69 | |
| Moins | 0,84 | 0,37 – 1,88 | 0,59 | 0,18 – 1,88 | |
| Peu | 0,55 | 0,18 – 1,64 | 3,82 | 1,05 – 13,9 | |
| Abréviations: IC = intervalle de confiance, OR = rapport de cotes | |||||
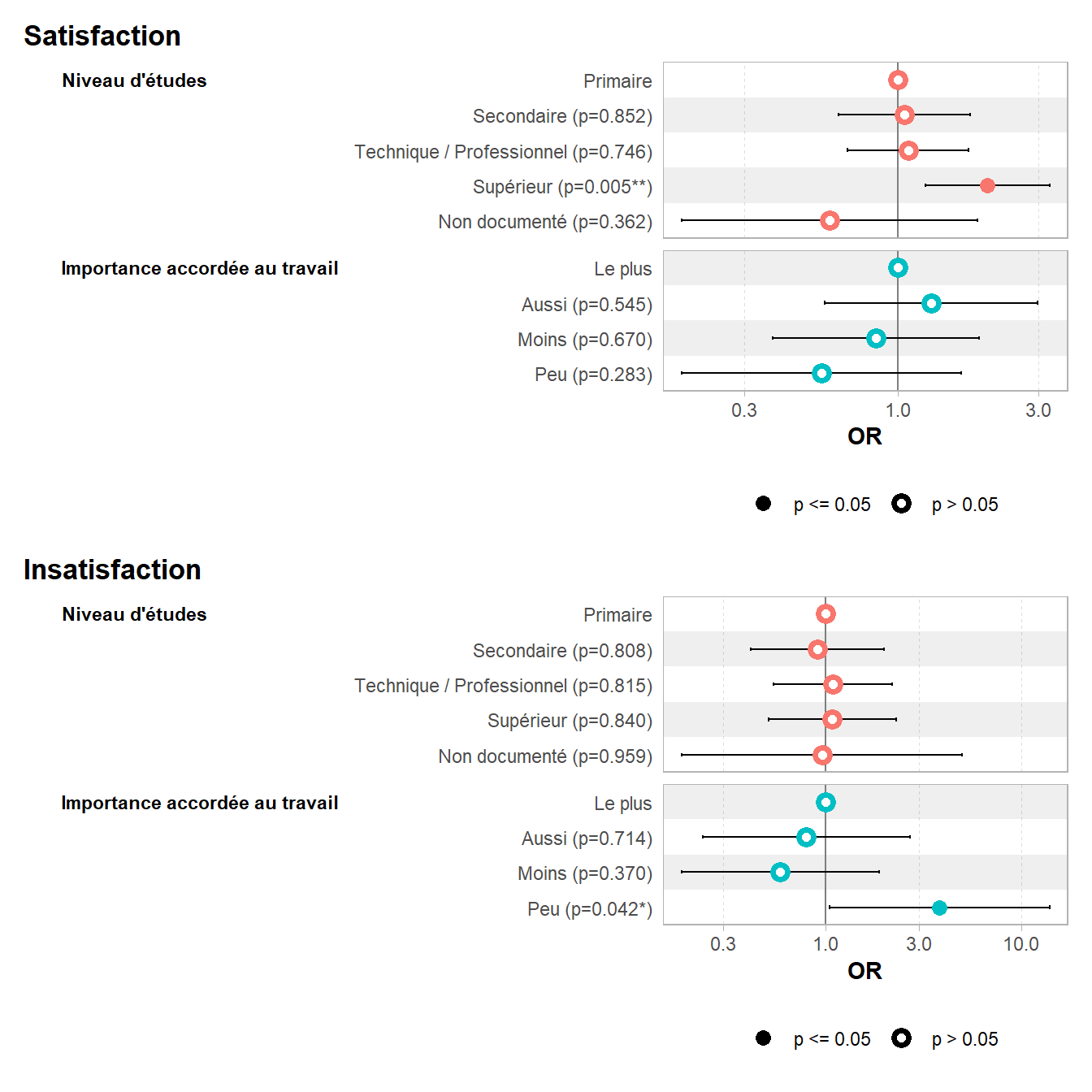
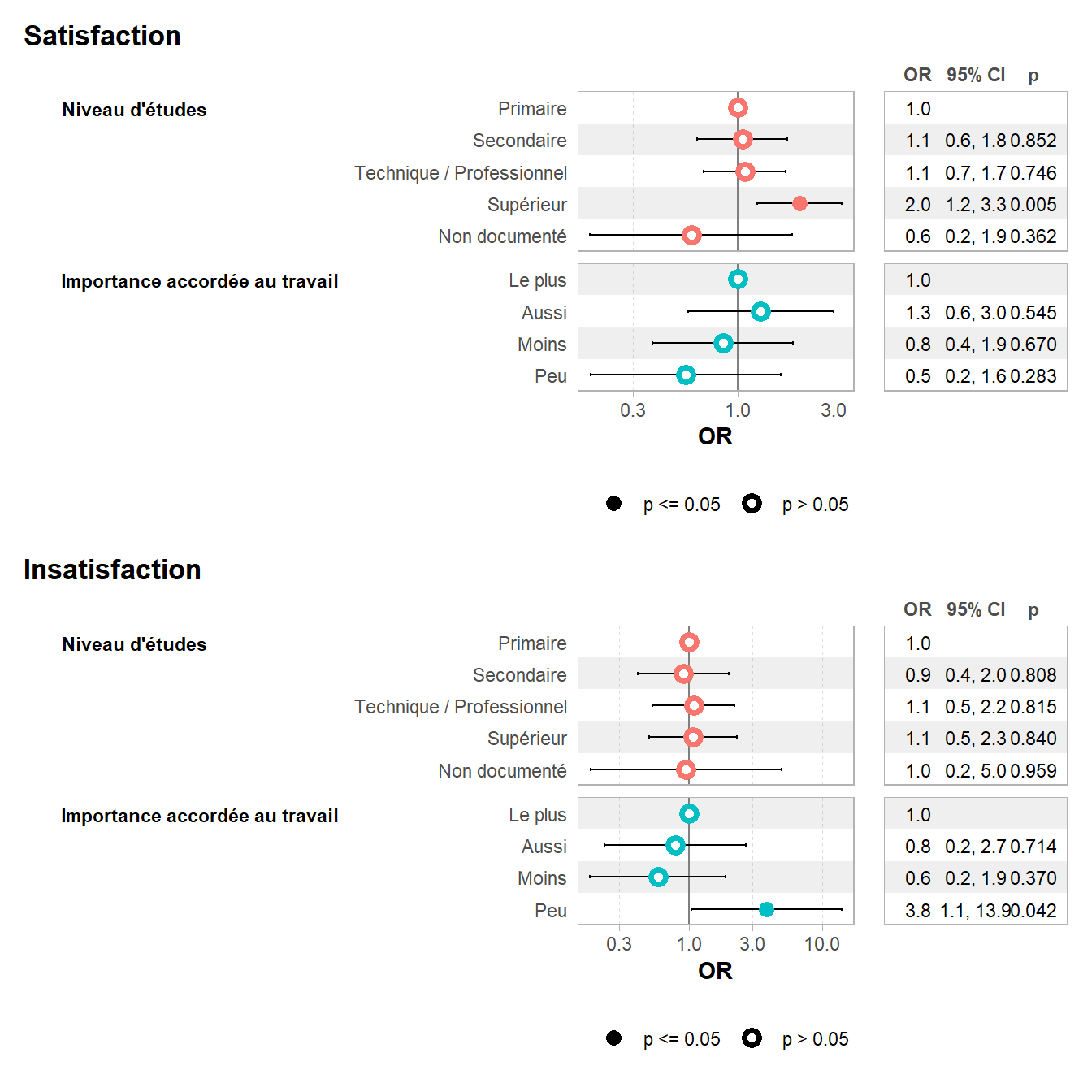
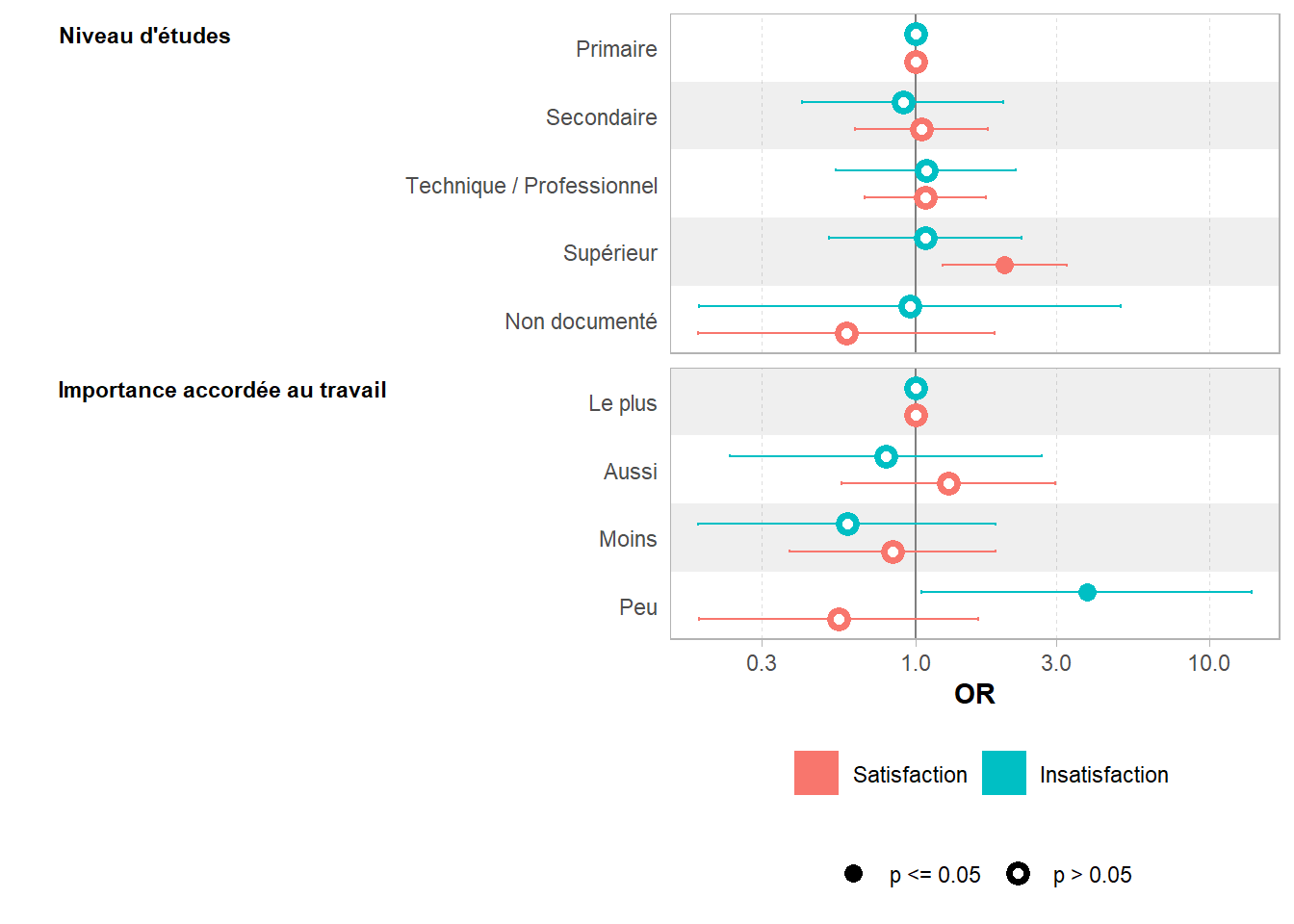
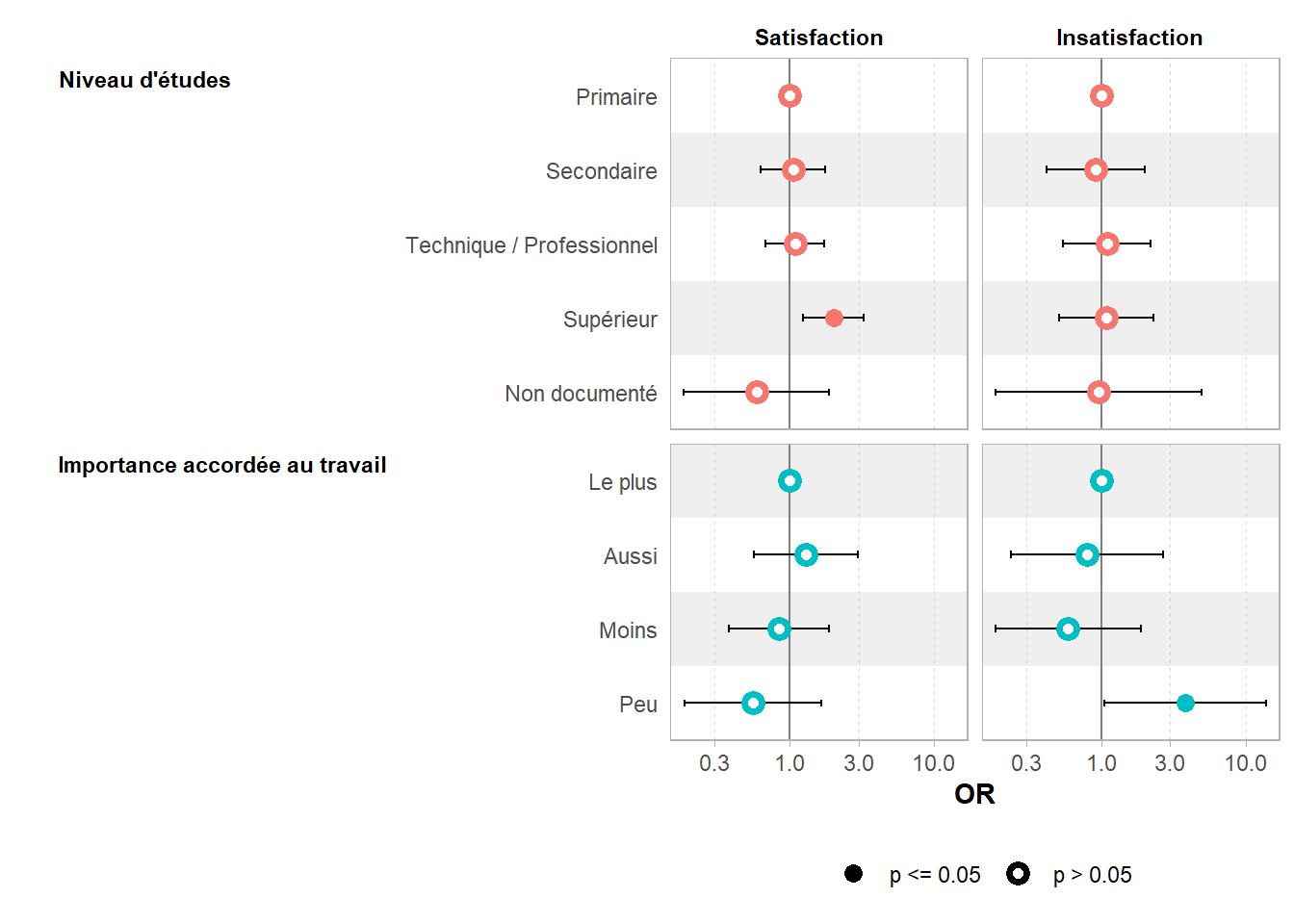
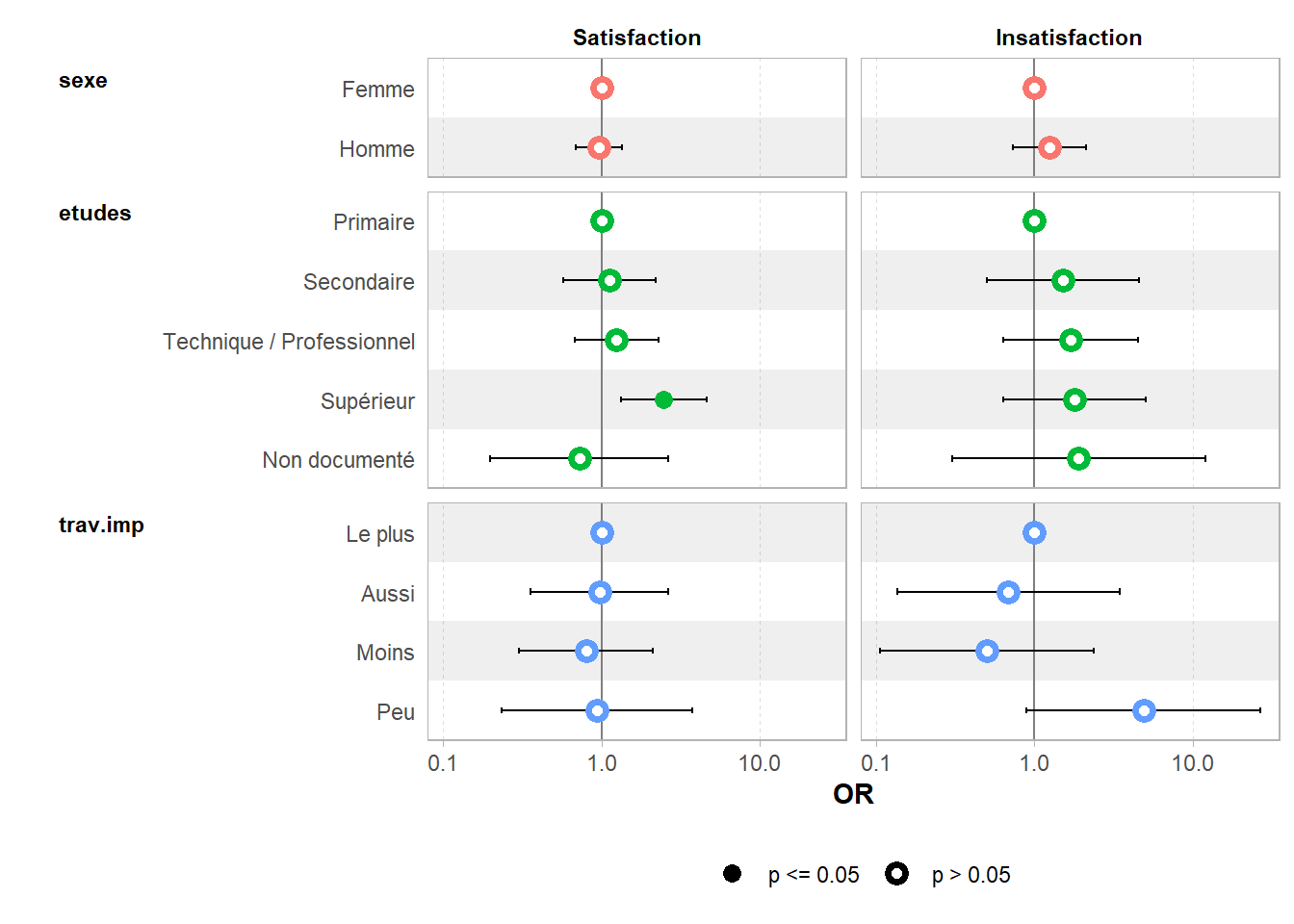
Pour un graphique des coefficients, on peut appeler directement ggstats::gcoef_model() ou encore ggstats::coef_table()3. De plus, ggstats propose également les variantes ggstats::gcoef_dodged() et ggstats::ggcoef_faceted().
3 Attention : pour que cela fonctionne avec un modèle multinomial, il est nécessaire d’utiliser la version 0.9.0 (ou une version plus récente) de ggstats.
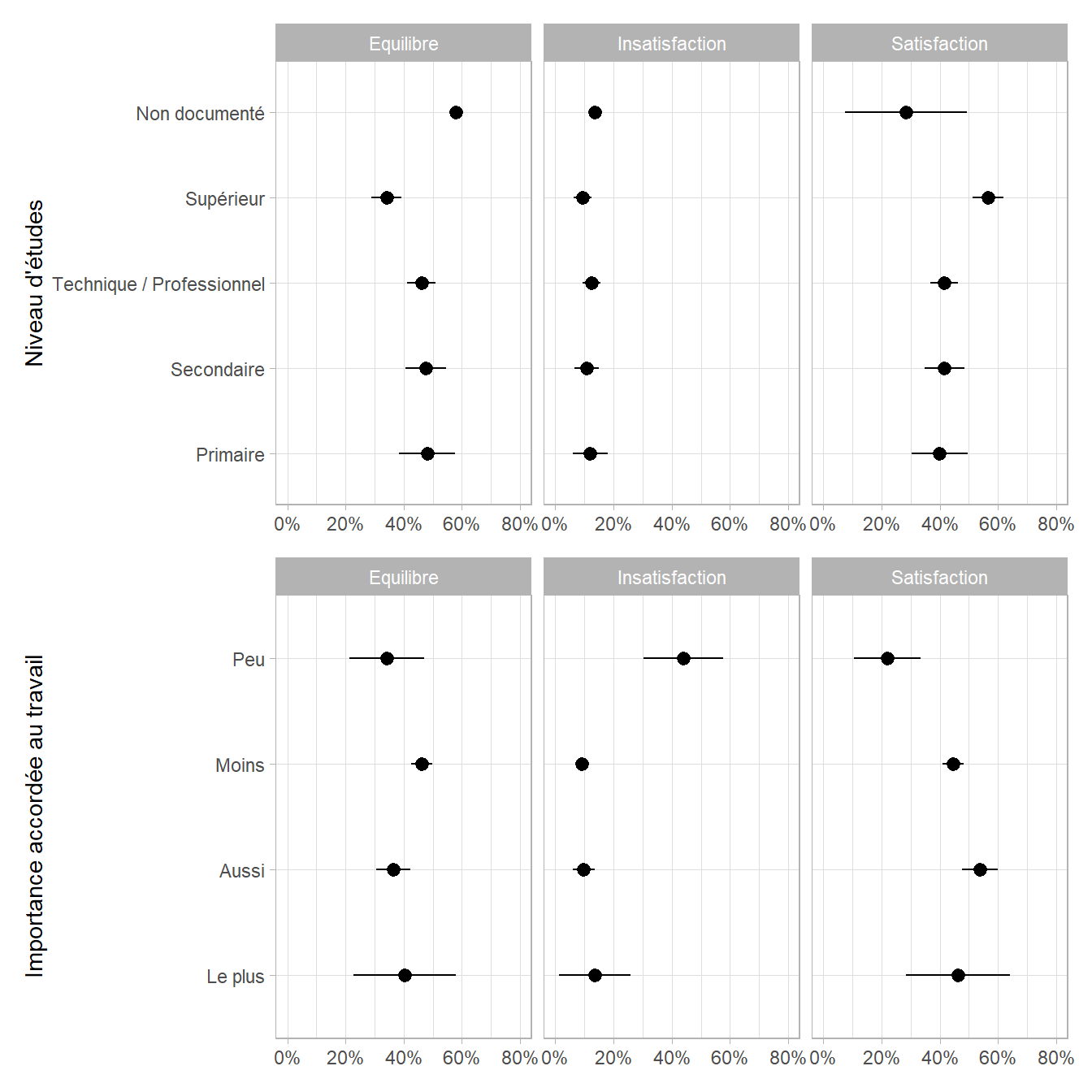
Pour faciliter l’interprétation, on pourra représenter les prédictions marginales du modèle (cf. Chapitre 24) avec broom.helpers::plot_marginal_predictions().
reg2 |>
broom.helpers::plot_marginal_predictions() |>
patchwork::wrap_plots(ncol = 1) &
scale_y_continuous(labels = scales::percent, limits = c(0, .8)) &
coord_flip()
Dans certaines situations, il peut être plus simple de réaliser plusieurs modèles logistiques binaires séparés plutôt qu’une régression multinomiale. Si la variable à expliquer a trois niveaux (A, B et C), on pourra réaliser un modèle binaire B vs A, et un modèle binaire C vs A. Cette approche est appelée approximation de Begg et Gray
. On trouvera, en anglais, plus d’explications et des références bibliographiques sur StackOverflow.
43.4 Données pondérées
L’extension survey (cf. Chapitre 28) ne fournit pas de fonction adaptée aux régressions multinomiales. Cependant, il est possible d’en réaliser une en ayant recours à des poids de réplication, comme suggéré par Thomas Lumley dans son ouvrage Complex Surveys: A Guide to Analysis Using R. Thomas Lumley est par ailleurs l’auteur de l’extension survey.
43.4.1 avec svrepmisc::svymultinom()
L’extension svrepmisc disponible sur GitHub fournit quelques fonctions facilitant l’utilisation des poids de réplication avec survey. Pour l’installer, on utilisera le code ci-dessous :
En premier lieu, il faut définir le design de notre tableau de données puis calculer des poids de réplication.
Il faut prévoir un nombre de replicates suffisant pour calculer ultérieurement les intervalles de confiance des coefficients. Plus ce nombre est élevé, plus précise sera l’estimation de la variance et donc des valeurs p et des intervalles de confiance. Cependant, plus ce nombre est élevé, plus le temps de calcul sera important. Pour gagner en temps de calcul, nous avons ici pris une valeur de 25, mais l’usage est de considérer au moins 1000 réplications.
svrepmisc fournit une fonction svrepmisc::svymultinom() pour le calcul d’une régression multinomiale avec des poids de réplication.
svrepmisc fournit également des méthodes svrepmisc::confint() et svrepmisc::tidy(). Nous pouvons donc calculer et afficher les odds ratio et leur intervalle de confiance.
Coefficient SE t value
Satisfaction.(Intercept) -0.116149 0.586601 -0.1980
Insatisfaction.(Intercept) -1.547056 2.663680 -0.5808
Satisfaction.sexeHomme -0.041405 0.167107 -0.2478
Insatisfaction.sexeHomme 0.221849 0.280504 0.7909
Satisfaction.etudesSecondaire 0.115722 0.361761 0.3199
Insatisfaction.etudesSecondaire 0.418476 0.430662 0.9717
Satisfaction.etudesTechnique / Professionnel 0.220702 0.284703 0.7752
Insatisfaction.etudesTechnique / Professionnel 0.529317 0.451425 1.1725
Satisfaction.etudesSupérieur 0.905852 0.279232 3.2441
Insatisfaction.etudesSupérieur 0.584499 0.440591 1.3266
Satisfaction.etudesNon documenté -0.323293 0.823426 -0.3926
Insatisfaction.etudesNon documenté 0.646168 6.477027 0.0998
Satisfaction.trav.impAussi -0.027506 0.537541 -0.0512
Insatisfaction.trav.impAussi -0.375642 2.666129 -0.1409
Satisfaction.trav.impMoins -0.220703 0.556930 -0.3963
Insatisfaction.trav.impMoins -0.694337 2.734109 -0.2540
Satisfaction.trav.impPeu -0.069034 0.816580 -0.0845
Insatisfaction.trav.impPeu 1.584747 2.626238 0.6034
Pr(>|t|)
Satisfaction.(Intercept) 0.84867
Insatisfaction.(Intercept) 0.57959
Satisfaction.sexeHomme 0.81142
Insatisfaction.sexeHomme 0.45496
Satisfaction.etudesSecondaire 0.75839
Insatisfaction.etudesSecondaire 0.36357
Satisfaction.etudesTechnique / Professionnel 0.46360
Insatisfaction.etudesTechnique / Professionnel 0.27933
Satisfaction.etudesSupérieur 0.01417 *
Insatisfaction.etudesSupérieur 0.22627
Satisfaction.etudesNon documenté 0.70628
Insatisfaction.etudesNon documenté 0.92333
Satisfaction.trav.impAussi 0.96062
Insatisfaction.trav.impAussi 0.89192
Satisfaction.trav.impMoins 0.70370
Insatisfaction.trav.impMoins 0.80683
Satisfaction.trav.impPeu 0.93499
Insatisfaction.trav.impPeu 0.56526
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 2.5 % 97.5 %
Satisfaction.(Intercept) -1.5032402 1.2709417
Insatisfaction.(Intercept) -7.8456579 4.7515451
Satisfaction.sexeHomme -0.4365498 0.3537389
Insatisfaction.sexeHomme -0.4414376 0.8851355
Satisfaction.etudesSecondaire -0.7397067 0.9711515
Insatisfaction.etudesSecondaire -0.5998781 1.4368308
Satisfaction.etudesTechnique / Professionnel -0.4525138 0.8939186
Insatisfaction.etudesTechnique / Professionnel -0.5381338 1.5967687
Satisfaction.etudesSupérieur 0.2455728 1.5661313
Insatisfaction.etudesSupérieur -0.4573318 1.6263305
Satisfaction.etudesNon documenté -2.2703858 1.6237990
Insatisfaction.etudesNon documenté -14.6695666 15.9619021
Satisfaction.trav.impAussi -1.2985878 1.2435755
Insatisfaction.trav.impAussi -6.6800359 5.9287522
Satisfaction.trav.impMoins -1.5376346 1.0962277
Insatisfaction.trav.impMoins -7.1594784 5.7708045
Satisfaction.trav.impPeu -1.9999383 1.8618696
Insatisfaction.trav.impPeu -4.6253178 7.7948122 term estimate std.error
1 Insatisfaction.(Intercept) 0.2128737 2.6636797
2 Insatisfaction.etudesNon documenté 1.9082140 6.4770267
3 Insatisfaction.etudesSecondaire 1.5196444 0.4306623
4 Insatisfaction.etudesSupérieur 1.7940926 0.4405906
5 Insatisfaction.etudesTechnique / Professionnel 1.6977731 0.4514253
6 Insatisfaction.sexeHomme 1.2483828 0.2805040
7 Insatisfaction.trav.impAussi 0.6868483 2.6661293
8 Insatisfaction.trav.impMoins 0.4994055 2.7341094
9 Insatisfaction.trav.impPeu 4.8780580 2.6262376
10 Satisfaction.(Intercept) 0.8903423 0.5866010
11 Satisfaction.etudesNon documenté 0.7237615 0.8234257
12 Satisfaction.etudesSecondaire 1.1226842 0.3617611
13 Satisfaction.etudesSupérieur 2.4740390 0.2792322
14 Satisfaction.etudesTechnique / Professionnel 1.2469523 0.2847032
15 Satisfaction.sexeHomme 0.9594401 0.1671066
16 Satisfaction.trav.impAussi 0.9728687 0.5375407
17 Satisfaction.trav.impMoins 0.8019545 0.5569304
18 Satisfaction.trav.impPeu 0.9332946 0.8165796
statistic p.value conf.low conf.high
1 -0.58079672 0.5795875 3.914480e-04 1.157630e+02
2 0.09976302 0.9233295 4.256848e-07 8.553936e+06
3 0.97170429 0.3635690 5.488786e-01 4.207341e+00
4 1.32662705 0.2262724 6.329703e-01 5.085180e+00
5 1.17254710 0.2793310 5.838368e-01 4.937053e+00
6 0.79089398 0.4549627 6.431112e-01 2.423313e+00
7 -0.14089407 0.8919224 1.255733e-03 3.756855e+02
8 -0.25395361 0.8068294 7.774600e-04 3.207957e+02
9 0.60342873 0.5652557 9.800540e-03 2.427973e+03
10 -0.19800382 0.8486695 2.224083e-01 3.564207e+00
11 -0.39262000 0.7062815 1.032723e-01 5.072323e+00
12 0.31988627 0.7583907 4.772539e-01 2.640984e+00
13 3.24408142 0.0141728 1.278353e+00 4.788089e+00
14 0.77520166 0.4635984 6.360273e-01 2.444691e+00
15 -0.24777846 0.8114169 6.462623e-01 1.424383e+00
16 -0.05117032 0.9606194 2.729169e-01 3.467991e+00
17 -0.39628549 0.7036967 2.148888e-01 2.992855e+00
18 -0.08454088 0.9349935 1.353436e-01 6.435758e+00Par contre, le support de gtsummary::tbl_regression() et ggstats::ggcoef_model() est plus limité. Vous pourrez afficher un tableau basique des résultats et un graphiques des coefficients, mais sans les enrichissements usuels (identification des variables, étiquettes propres, identification des niveaux, etc.).
43.4.2 avec svyVGAM::svy_glm()
Une alternative possible pour le calcul de la régression logistique multinomiale avec des données pondérées est svyVGAM::svy_vglm() avec family = VGAM::multinomial.
Nous allons commencer par définir le plan d’échantillonnage.
Puis, on appelle svyVGAM::svy_vglm() en précisant family = VGAM::multinomial. Par défaut, VGAM::multinomial() utilise la dernière modalité de la variable d’intérêt comme modalité de référence. Cela est modifiable avec refLevel.
regm2 <- svyVGAM::svy_vglm(
trav.satisf ~ sexe + etudes + trav.imp,
family = VGAM::multinomial(refLevel = "Equilibre"),
design = dw
)
regm2 |> summary()svy_vglm.survey.design(trav.satisf ~ sexe + etudes + trav.imp,
family = VGAM::multinomial(refLevel = "Equilibre"), design = dw)
Independent Sampling design (with replacement)
Called via srvyr
Sampling variables:
- ids: `1`
- weights: poids
Data variables:
- id (int), age (int), sexe (fct), nivetud (fct), poids (dbl), occup (fct),
qualif (fct), freres.soeurs (int), clso (fct), relig (fct), trav.imp (fct),
trav.satisf (fct), hard.rock (fct), lecture.bd (fct), peche.chasse (fct),
cuisine (fct), bricol (fct), cinema (fct), sport (fct), heures.tv (dbl),
groupe_ages (fct), etudes (fct)
Coef SE z p
(Intercept):1 -0.116117 0.553242 -0.2099 0.833757
(Intercept):2 -1.547693 0.876195 -1.7664 0.077332
sexeHomme:1 -0.041412 0.171351 -0.2417 0.809029
sexeHomme:2 0.221930 0.272669 0.8139 0.415693
etudesSecondaire:1 0.115688 0.341830 0.3384 0.735034
etudesSecondaire:2 0.418102 0.563205 0.7424 0.457868
etudesTechnique / Professionnel:1 0.220662 0.310123 0.7115 0.476754
etudesTechnique / Professionnel:2 0.529020 0.501080 1.0558 0.291079
etudesSupérieur:1 0.905798 0.314513 2.8800 0.003977
etudesSupérieur:2 0.584320 0.525633 1.1116 0.266289
etudesNon documenté:1 -0.323271 0.662511 -0.4879 0.625587
etudesNon documenté:2 0.646195 0.939745 0.6876 0.491687
trav.impAussi:1 -0.027517 0.511636 -0.0538 0.957109
trav.impAussi:2 -0.374881 0.825214 -0.4543 0.649625
trav.impMoins:1 -0.220706 0.494951 -0.4459 0.655659
trav.impMoins:2 -0.693571 0.792031 -0.8757 0.381200
trav.impPeu:1 -0.069004 0.706959 -0.0976 0.922244
trav.impPeu:2 1.585521 0.866529 1.8297 0.067289Là encore, le support de gtsummary::tbl_regression() sera limité4. Pour calculer les odds ratios avec leurs intervalles de confiance, on pourra avoir recours à broom.helpers::tidy_svy_vglm(), dédié justement à ce type de modèles5.
4 Du moins, avec la version stable actuelle de gtsummary (la version 2.2.0). Par contre, le support est intégré à la version de développement et sera donc disponible dans la prochaine version stable.
5 Cette fonction a été introduite dans la version 1.21.0 de broom.helpers. Pensez à éventuellement mettre à jour le package.
original_term term group
1 (Intercept):1 (Intercept) 1
2 (Intercept):2 (Intercept) 2
3 sexeHomme:1 sexeHomme 1
4 sexeHomme:2 sexeHomme 2
5 etudesSecondaire:1 etudesSecondaire 1
6 etudesSecondaire:2 etudesSecondaire 2
7 etudesTechnique / Professionnel:1 etudesTechnique / Professionnel 1
8 etudesTechnique / Professionnel:2 etudesTechnique / Professionnel 2
9 etudesSupérieur:1 etudesSupérieur 1
10 etudesSupérieur:2 etudesSupérieur 2
11 etudesNon documenté:1 etudesNon documenté 1
12 etudesNon documenté:2 etudesNon documenté 2
13 trav.impAussi:1 trav.impAussi 1
14 trav.impAussi:2 trav.impAussi 2
15 trav.impMoins:1 trav.impMoins 1
16 trav.impMoins:2 trav.impMoins 2
17 trav.impPeu:1 trav.impPeu 1
18 trav.impPeu:2 trav.impPeu 2
estimate std.error conf.level conf.low conf.high statistic df.error
1 0.8903708 0.4925908 0.95 0.30105802 2.633247 -0.20988509 Inf
2 0.2127382 0.1864002 0.95 0.03819678 1.184853 -1.76637893 Inf
3 0.9594340 0.1643997 0.95 0.68574259 1.342360 -0.24167835 Inf
4 1.2484837 0.3404228 0.95 0.73162172 2.130488 0.81391637 Inf
5 1.1226456 0.3837540 0.95 0.57448201 2.193860 0.33843739 Inf
6 1.5190753 0.8555505 0.95 0.50370762 4.581209 0.74236198 Inf
7 1.2469025 0.3866926 0.95 0.67897791 2.289862 0.71153296 Inf
8 1.6972676 0.8504673 0.95 0.63566751 4.531799 1.05575832 Inf
9 2.4739057 0.7780767 0.95 1.33557655 4.582448 2.87999791 Inf
10 1.7937708 0.9428657 0.95 0.64024629 5.025587 1.11164951 Inf
11 0.7237778 0.4795111 0.95 0.19754885 2.651771 -0.48794745 Inf
12 1.9082659 1.7932841 0.95 0.30250055 12.037925 0.68762767 Inf
13 0.9728582 0.4977496 0.95 0.35689786 2.651888 -0.05378223 Inf
14 0.6873710 0.5672279 0.95 0.13638549 3.464290 -0.45428375 Inf
15 0.8019528 0.3969271 0.95 0.30398071 2.115688 -0.44591425 Inf
16 0.4997879 0.3958473 0.95 0.10582985 2.360279 -0.87568771 Inf
17 0.9333229 0.6598208 0.95 0.23348961 3.730751 -0.09760692 Inf
18 4.8818349 4.2302506 0.95 0.89328990 26.679258 1.82973852 Inf
p.value component y.level
1 0.833757356 log(mu[,2]/mu[,1]) Satisfaction
2 0.077332298 log(mu[,3]/mu[,1]) Insatisfaction
3 0.809029407 log(mu[,2]/mu[,1]) Satisfaction
4 0.415692863 log(mu[,3]/mu[,1]) Insatisfaction
5 0.735033605 log(mu[,2]/mu[,1]) Satisfaction
6 0.457868051 log(mu[,3]/mu[,1]) Insatisfaction
7 0.476754032 log(mu[,2]/mu[,1]) Satisfaction
8 0.291078645 log(mu[,3]/mu[,1]) Insatisfaction
9 0.003976778 log(mu[,2]/mu[,1]) Satisfaction
10 0.266288875 log(mu[,3]/mu[,1]) Insatisfaction
11 0.625587062 log(mu[,2]/mu[,1]) Satisfaction
12 0.491687277 log(mu[,3]/mu[,1]) Insatisfaction
13 0.957108667 log(mu[,2]/mu[,1]) Satisfaction
14 0.649624613 log(mu[,3]/mu[,1]) Insatisfaction
15 0.655659186 log(mu[,2]/mu[,1]) Satisfaction
16 0.381199829 log(mu[,3]/mu[,1]) Insatisfaction
17 0.922244427 log(mu[,2]/mu[,1]) Satisfaction
18 0.067289048 log(mu[,3]/mu[,1]) InsatisfactionPar contre, les dernières versions de ggstats sont compatibles avec ce type de modèle. On pourra donc utiliser les fonctions ggcoef_*().
43.5 webin-R
La régression logistique multinomiale est abordée dans le webin-R #20 (trajectoires de soins : un exemple de données longitudinales (4)) sur YouTube.