27  Multicolinéarité

Dans une régression, la multicolinéarité est un problème qui survient lorsque certaines variables de prévision du modèle mesurent le même phénomène. Une multicolinéarité prononcée s’avère problématique, car elle peut augmenter la variance des coefficients de régression et les rendre instables et difficiles à interpréter. Les conséquences de coefficients instables peuvent être les suivantes :

La multicolinéarité n’a aucune incidence sur l’adéquation de l’ajustement, ni sur la qualité de la prévision. Cependant, les coefficients individuels associés à chaque variable explicative ne peuvent pas être interprétés de façon fiable.

27.1 Définition

Au sens strict, on parle de multicolinéarité parfaite lorsqu’une des variables explicatives d’un modèle est une combinaison linéaire d’une ou plusieurs autres variables explicatives introduites dans le même modèle. L’absence de multicolinéarité parfaite est une des conditions requises pour pouvoir estimer un modèle linéaire et, par extension, un modèle linéaire généralisé (dont les modèles de régression logistique).

Dans les faits, une multicolinéarité parfaite n’est quasiment jamais observée. Mais une forte multicolinéarité entre plusieurs variables peut poser problème dans l’estimation et l’interprétation d’un modèle.

Une erreur fréquente est de confondre multicolinéarité et corrélation. Si des variables colinéaires sont de facto fortement corrélées entre elles, deux variables corrélées ne sont pas forcément colinéaires. En termes non statistiques, il y a colinéarité lorsque deux ou plusieurs variables mesurent la même chose.

Prenons un exemple. Nous étudions les complications après l’accouchement dans différentes maternités d’un pays en développement. On souhaite mettre dans le modèle, à la fois le milieu de résidence (urbain ou rural) et le fait qu’il y ait ou non un médecin dans la clinique. Or, dans la zone d’enquête, les maternités rurales sont dirigées seulement par des sage-femmes tandis que l’on trouve un médecin dans toutes les maternités urbaines sauf une. Dès lors, dans ce contexte précis, le milieu de résidence prédit presque totalement la présence d’un médecin et on se retrouve face à une multicolinéarité (qui serait même parfaite s’il n’y avait pas une clinique urbaine sans médecin). On ne peut donc distinguer l’effet de la présence d’un médecin de celui du milieu de résidence et il ne faut mettre qu’une seule de ces deux variables dans le modèle, sachant que du point de vue de l’interprétation elle capturera à la fois l’effet de la présence d’un médecin et celui du milieu de résidence.

Par contre, si dans notre région d’étude, seule la moitié des maternités urbaines disposait d’un médecin, alors le milieu de résidence n’aurait pas été suffisant pour prédire la présence d’un médecin. Certes, les deux variables seraient corrélées mais pas colinéaires. Un autre exemple de corrélation sans colinéarité, c’est la relation entre milieu de résidence et niveau d’instruction. Il y a une corrélation entre ces deux variables, les personnes résidant en ville étant généralement plus instruites. Cependant, il existe également des personnes non instruites en ville et des personnes instruites en milieu rural. Le milieu de résidence n’est donc pas suffisant pour prédire le niveau d’instruction.

27.2 Mesure de la colinéarité

Il existe différentes mesures de la multicolinéarité. L’extension {mctest} en fournie plusieurs, mais elle n’est utilisable que si l’ensemble des variables explicatives sont de type numérique.

L’approche la plus classique consiste à examiner les facteurs d’inflation de la variance (FIV) ou variance inflation factor (VIF) en anglais. Les FIV estiment de combien la variance d’un coefficient est augmentée en raison d’une relation linéaire avec d’autres prédicteurs. Ainsi, un FIV de 1,8 nous dit que la variance de ce coefficient particulier est supérieure de 80 % à la variance que l’on aurait dû observer si ce facteur n’est absolument pas corrélé aux autres prédicteurs.

Si tous les FIV sont égaux à 1, il n’existe pas de multicolinéarité, mais si certains FIV sont supérieurs à 1, les prédicteurs sont corrélés. Il n’y a pas de consensus sur la valeur au-delà de laquelle on doit considérer qu’il y a multicolinéarité. Certains auteurs, comme Paul Allison1, disent de regarder plus en détail les variables avec un FIV supérieur à 2,5. D’autres ne s’inquiètent qu’à partir de 5. Il n’existe pas de test statistique qui permettrait de dire s’il y a colinéarité ou non2.

2 Pour plus de détails, voir ce post de Davig Giles, Can You Actually TEST for Multicollinearity?, qui explique pourquoi ce n’est pas possible.

L’extension car fournit une fonction car::vif() permettant de calculer les FIV à partir d’un modèle. Elle implémente même une version généralisée permettant de considérer des facteurs catégoriels et des modèles linéaires généralisés comme la régression logistique.

Reprenons, pour exemple, un modèle logistique que nous avons déjà abordé dans d’autres chapitres.

library(tidyverse)
library(labelled)

data(hdv2003, package = "questionr")

d <-
  hdv2003 |> 
  mutate(
    sexe = sexe |> fct_relevel("Femme"),
    groupe_ages = age |>
      cut(
        c(18, 25, 45, 65, 99),
        right = FALSE,
        include.lowest = TRUE,
        labels = c("18-24 ans", "25-44 ans",
                   "45-64 ans", "65 ans et plus")
      ),
    etudes = nivetud |> 
      fct_recode(
        "Primaire" = "N'a jamais fait d'etudes",
        "Primaire" = "A arrete ses etudes, avant la derniere annee d'etudes primaires",
        "Primaire" = "Derniere annee d'etudes primaires",
        "Secondaire" = "1er cycle",
        "Secondaire" = "2eme cycle",
        "Technique / Professionnel" = "Enseignement technique ou professionnel court",
        "Technique / Professionnel" = "Enseignement technique ou professionnel long",
        "Supérieur" = "Enseignement superieur y compris technique superieur"
    ) |> 
    fct_na_value_to_level("Non documenté")  
  ) |> 
  set_variable_labels(
    sport = "Pratique un sport ?",
    sexe = "Sexe",
    groupe_ages = "Groupe d'âges",
    etudes = "Niveau d'études",
    heures.tv = "Heures de télévision / jour"
  )

mod <- glm(
  sport ~ sexe + groupe_ages + etudes + heures.tv,
  family = binomial,
  data = d
)

Le calcul des FIV se fait simplement en passant le modèle à la fonction car::vif().

mod |> car::vif()
                GVIF Df GVIF^(1/(2*Df))
sexe        1.024640  1        1.012245
groupe_ages 1.745492  3        1.097285
etudes      1.811370  4        1.077087
heures.tv   1.057819  1        1.028503

Dans notre exemple, tous les FIV sont proches de 1. Il n’y a donc pas de problème potentiel de colinéarité à explorer.

Pour un tableau propre, nous pouvons aussi utiliser gtsummary::add_vif().

library(gtsummary)
theme_gtsummary_language(
  "fr",
  decimal.mark = ",",
  big.mark = " "
)
mod |> 
  tbl_regression(exponentiate = TRUE) |> 
  bold_labels() |> 
  add_vif()

Caractéristique

OR

1

95% IC

1

p-valeur

GVIF

1

Adjusted GVIF

2,1
Sexe


1,0 1,0
    Femme — —


    Homme 1,52 1,24 – 1,87 <0,001

Groupe d'âges


1,7 1,1
    18-24 ans — —


    25-44 ans 0,68 0,43 – 1,06 0,084

    45-64 ans 0,36 0,23 – 0,57 <0,001

    65 ans et plus 0,27 0,16 – 0,46 <0,001

Niveau d'études


1,8 1,1
    Primaire — —


    Secondaire 2,54 1,73 – 3,75 <0,001

    Technique / Professionnel 2,81 1,95 – 4,10 <0,001

    Supérieur 6,55 4,50 – 9,66 <0,001

    Non documenté 8,54 4,51 – 16,5 <0,001

Heures de télévision / jour 0,89 0,83 – 0,95 <0,001 1,1 1,0
1

OR = rapport de cotes, IC = intervalle de confiance, GVIF = Generalized Variance Inflation Factor
2

GVIF3

3 1/(2*df)

Table 27.1: Résumé du modèle logistique simple avec affichage des VIF généralisés

Le package performance propose quant à lui une fonction performance::check_collinearity() pour le calcul des FIV et de leur intervalle de confiance.

mod |> performance::check_collinearity()
# Check for Multicollinearity

Low Correlation

        Term  VIF   VIF 95% CI Increased SE Tolerance Tolerance 95% CI
        sexe 1.02 [1.00, 1.16]         1.01      0.98     [0.86, 1.00]
 groupe_ages 1.75 [1.64, 1.86]         1.32      0.57     [0.54, 0.61]
      etudes 1.81 [1.70, 1.93]         1.35      0.55     [0.52, 0.59]
   heures.tv 1.06 [1.02, 1.13]         1.03      0.95     [0.88, 0.98]

Les variables avec un FIV entre 5 et 10 sont présentées comme ayant une corrélation moyenne et celles avec un FIV de 10 ou plus une corrélation forte. Prenons un autre exemple.

mod2 <- lm(mpg ~ wt + am + gear + vs * cyl, data = mtcars)
mc <- mod2 |> performance::check_collinearity()
Model has interaction terms. VIFs might be inflated.
  You may check multicollinearity among predictors of a model without
  interaction terms.
mc
# Check for Multicollinearity

Low Correlation

 Term  VIF     VIF 95% CI Increased SE Tolerance Tolerance 95% CI
   wt 3.64 [ 2.46,  5.77]         1.91      0.27     [0.17, 0.41]
   am 4.32 [ 2.88,  6.89]         2.08      0.23     [0.15, 0.35]
 gear 3.06 [ 2.11,  4.82]         1.75      0.33     [0.21, 0.47]

Moderate Correlation

 Term  VIF     VIF 95% CI Increased SE Tolerance Tolerance 95% CI
  cyl 7.87 [ 5.03, 12.70]         2.80      0.13     [0.08, 0.20]

High Correlation

   Term   VIF     VIF 95% CI Increased SE Tolerance Tolerance 95% CI
     vs 38.55 [23.69, 63.15]         6.21      0.03     [0.02, 0.04]
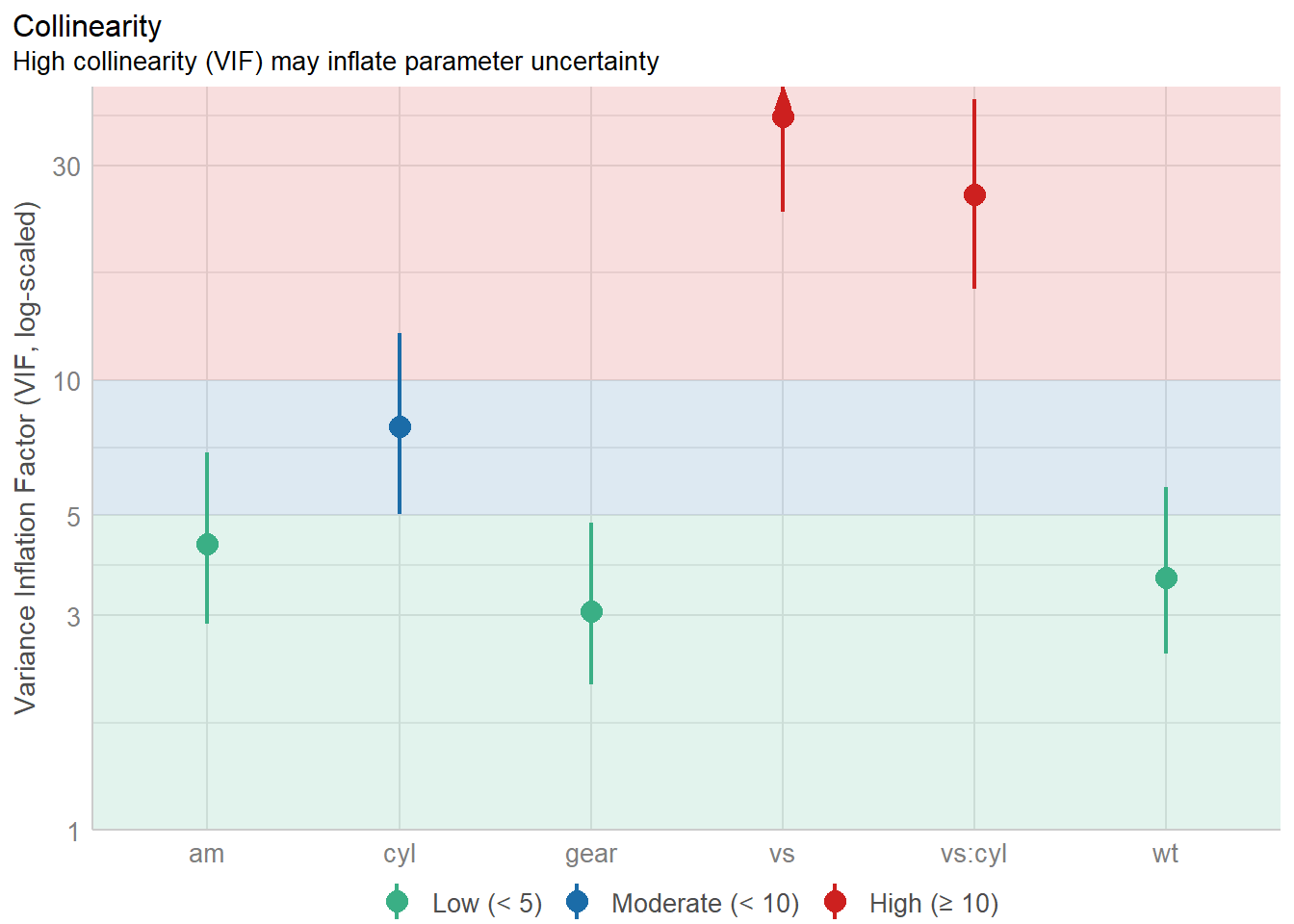
 vs:cyl 25.79 [15.93, 42.16]         5.08      0.04     [0.02, 0.06]

Une représentation graphique des FIV peut être obtenue avec plot() appliquée au résultat de performance::check_collinearity().

plot(mc)
Variable `Component` is not in your data frame :/
Figure 27.1: Représentation graphique des FIV d’un modèle

La fonction performance::print_md() peut être utilisée quant à elle pour une sortie des résultats dans un rapport markdown.

mc |> performance::print_md()
Term VIF VIF_CI_low VIF_CI_high SE_factor Tolerance Tolerance_CI_low Tolerance_CI_high
wt 3.64 2.46 5.77 1.91 0.27 0.17 0.41
am 4.32 2.88 6.89 2.08 0.23 0.15 0.35
gear 3.06 2.11 4.82 1.75 0.33 0.21 0.47
vs 38.55 23.69 63.15 6.21 0.03 0.02 0.04
cyl 7.87 5.03 12.70 2.80 0.13 0.08 0.20
vs:cyl 25.79 15.93 42.16 5.08 0.04 0.02 0.06
Table 27.2: Table des FIV d’un modèle

27.3 La multicolinéarité est-elle toujours un problème ?

Là encore, il n’y a pas de consensus sur cette question. Certains analystes considèrent que tout modèle où certains prédicteurs seraient colinéaires n’est pas valable. Dans le billet When Can You Safely Ignore Multicollinearity?, Paul Allison évoque quant à lui des situations où la multicolinéarité peut être ignorée en toute sécurité. Le texte ci-dessous est une traduction de ce billet.

1. Les variables avec des FIV élevés sont des variables de contrôle, et les variables d’intérêt n’ont pas de FIV élevés.

Voici le problème de la multicolinéarité : ce n’est un problème que pour les variables qui sont colinéaires. Il augmente les erreurs-types de leurs coefficients et peut rendre ces coefficients instables de plusieurs façons. Mais tant que les variables colinéaires ne sont utilisées que comme variables de contrôle, et qu’elles ne sont pas colinéaires avec vos variables d’intérêt, il n’y a pas de problème. Les coefficients des variables d’intérêt ne sont pas affectés et la performance des variables de contrôle n’est pas altérée.

Voici un exemple tiré de ces propres travaux : l’échantillon est constitué de collèges américains, la variable dépendante est le taux d’obtention de diplôme et la variable d’intérêt est un indicateur (factice) pour les secteurs public et privé. Deux variables de contrôle sont les scores moyens au SAT et les scores moyens à l’ACT pour l’entrée en première année. Ces deux variables ont une corrélation supérieure à ,9, ce qui correspond à des FIV d’au moins 5,26 pour chacune d’entre elles. Mais le FIV pour l’indicateur public/privé n’est que de 1,04. Il n’y a donc pas de problème à se préoccuper et il n’est pas nécessaire de supprimer l’un ou l’autre des deux contrôles, à condition que l’on ne cherche pas à interpréter ou comparer l’un par rapport à l’autre les coefficients de ces deux variables de contrôle.

2. Les FIV élevés sont causés par l’inclusion de puissances ou de produits d’autres variables.

Si vous spécifiez un modèle de régression avec x et x2, il y a de bonnes chances que ces deux variables soient fortement corrélées. De même, si votre modèle a x, z et xz, x et z sont susceptibles d’être fortement corrélés avec leur produit. Il n’y a pas de quoi s’inquiéter, car la valeur p de xz n’est pas affectée par la multicolinéarité. Ceci est facile à démontrer : vous pouvez réduire considérablement les corrélations en centrant les variables (c’est-à-dire en soustrayant leurs moyennes) avant de créer les puissances ou les produits. Mais la valeur p pour x2 ou pour xz sera exactement la même, que l’on centre ou non. Et tous les résultats pour les autres variables (y compris le R2 mais sans les termes d’ordre inférieur) seront les mêmes dans les deux cas. La multicolinéarité n’a donc pas de conséquences négatives.

3. Les variables avec des FIV élevés sont des variables indicatrices (factices) qui représentent une variable catégorielle avec trois catégories ou plus.

Si la proportion de cas dans la catégorie de référence est faible, les variables indicatrices auront nécessairement des FIV élevés, même si la variable catégorielle n’est pas associée à d’autres variables dans le modèle de régression.

Supposons, par exemple, qu’une variable de l’état matrimonial comporte trois catégories : actuellement marié, jamais marié et anciennement marié. Vous choisissez anciennement marié comme catégorie de référence, avec des variables d’indicateur pour les deux autres. Ce qui se passe, c’est que la corrélation entre ces deux indicateurs devient plus négative à mesure que la fraction de personnes dans la catégorie de référence diminue. Par exemple, si 45 % des personnes ne sont jamais mariées, 45 % sont mariées et 10 % sont anciennement mariées, les valeurs du FIV pour les personnes mariées et les personnes jamais mariées seront d’au moins 3,0.

Est-ce un problème ? Eh bien, cela signifie que les valeurs p des variables indicatrices peuvent être élevées. Mais le test global selon lequel tous les indicateurs ont des coefficients de zéro n’est pas affecté par des FIV élevés. Et rien d’autre dans la régression n’est affecté. Si vous voulez vraiment éviter des FIV élevés, il suffit de choisir une catégorie de référence avec une plus grande fraction des cas. Cela peut être souhaitable pour éviter les situations où aucun des indicateurs individuels n’est statistiquement significatif, même si l’ensemble des indicateurs est significatif.

27.4 webin-R

La multicolinéarité est abordée dans le webin-R #07 (régression logistique partie 2) sur YouTube.