library(tidyverse)
library(labelled)
library(gtsummary)
theme_gtsummary_language(
"fr",
decimal.mark = ",",
big.mark = " "
)
data(hdv2003, package = "questionr")
d <-
hdv2003 |>
mutate(
sexe = sexe |> fct_relevel("Femme"),
groupe_ages = age |>
cut(
c(18, 25, 45, 65, 99),
right = FALSE,
include.lowest = TRUE,
labels = c("18-24 ans", "25-44 ans",
"45-64 ans", "65 ans et plus")
),
etudes = nivetud |>
fct_recode(
"Primaire" = "N'a jamais fait d'etudes",
"Primaire" = "A arrete ses etudes, avant la derniere annee d'etudes primaires",
"Primaire" = "Derniere annee d'etudes primaires",
"Secondaire" = "1er cycle",
"Secondaire" = "2eme cycle",
"Technique / Professionnel" = "Enseignement technique ou professionnel court",
"Technique / Professionnel" = "Enseignement technique ou professionnel long",
"Supérieur" = "Enseignement superieur y compris technique superieur"
) |>
fct_na_value_to_level("Non documenté")
) |>
set_variable_labels(
sport = "Pratique un sport ?",
sexe = "Sexe",
groupe_ages = "Groupe d'âges",
etudes = "Niveau d'études",
relig = "Rapport à la religion",
lecture.bd = "Lit des bandes dessinées ?"
)
mod <- glm(
sport ~ sexe + groupe_ages + etudes + relig + lecture.bd,
family = binomial,
data = d
)23 Sélection pas à pas d’un modèle réduit
Il est toujours tentant lorsque l’on recherche les facteurs associés à un phénomène d’inclure un nombre important de variables explicatives potentielles dans son modèle de régression. Cependant, un tel modèle n’est pas forcément le plus efficace et certaines variables n’auront probablement pas d’effet significatif sur la variable d’intérêt.
Un autre problème potentiel est celui dur sur-ajustement ou surappentissage. Un modèle sur-ajusté est un modèle statistique qui contient plus de paramètres que ne peuvent le justifier les données. Dès lors, il va être trop ajusté aux données observées mais perdre en capacité de généralisation.
Pour une présentation didactique du cadre théorique de la sélection de modèle, vous pouvez consulter en ligne le cours de L. Rouvière sur la sélection/validation de modèles.
Les techniques de sélection pas à pas sont des approches visant à améliorer
un modèle explicatif. On part d’un modèle initial puis on regarde s’il est possible d’améliorer le modèle en ajoutant ou en supprimant une des variables du modèle pour obtenir un nouveau modèle. Le processus est répété jusqu’à obtenir un modèle final que l’on ne peut plus améliorer.
23.1 Données d’illustration
Pour illustrer ce chapitre, nous allons prendre un modèle logistique inspiré de celui utilisé dans le chapitre sur la régression logistique binaire (cf. Chapitre 22).
23.2 Présentation de l’AIC
Il faut définir un critère pour déterminer la qualité d’un modèle. L’un des plus utilisés est le Akaike Information Criterion ou AIC. Il s’agit d’un compromis entre le nombre de degrés de liberté (e.g. le nombre de coefficients dans le modèle) que l’on cherche à minimiser et la variance expliquée que l’on cherche à maximiser (la vraisemblance).
Plus précisément \(AIC=2k-2ln(L)\) où \(L\) est le maximum de la fonction de vraisemblance du modèle et \(k\) le nombre de paramètres (i.e. de coefficients) du modèle. Plus l’AIC sera faible, meilleur sera le modèle.
L’AIC d’un modèle s’obtient aisément avec AIC().
23.3 Sélection pas à pas descendante
La fonction step() permet de sélectionner le meilleur modèle par une procédure pas à pas descendante basée sur la minimisation de l’AIC. La fonction affiche à l’écran les différentes étapes de la sélection et renvoie le modèle final.
Start: AIC=2257.1
sport ~ sexe + groupe_ages + etudes + relig + lecture.bd
Df Deviance AIC
- relig 5 2231.9 2251.9
- lecture.bd 1 2227.9 2255.9
<none> 2227.1 2257.1
- sexe 1 2245.6 2273.6
- groupe_ages 3 2280.1 2304.1
- etudes 4 2375.5 2397.5
Step: AIC=2251.95
sport ~ sexe + groupe_ages + etudes + lecture.bd
Df Deviance AIC
- lecture.bd 1 2232.6 2250.6
<none> 2231.9 2251.9
- sexe 1 2248.8 2266.8
- groupe_ages 3 2282.1 2296.1
- etudes 4 2380.5 2392.5
Step: AIC=2250.56
sport ~ sexe + groupe_ages + etudes
Df Deviance AIC
<none> 2232.6 2250.6
- sexe 1 2249.2 2265.2
- groupe_ages 3 2282.5 2294.5
- etudes 4 2385.2 2395.2Le modèle initial a un AIC de 2257,1.
À la première étape, il apparaît que la suppression de la variable relig permettrait diminuer l’AIC à 2251,9 et la suppression de la variable lecture.bd de le diminuer à 2255,9. Le gain maximal est obtenu en supprimant relig et donc cette variable est supprimée à ce stade. On peut noter que la suppression de la variable entraîne de facto une augmentation des résidus (colonne Deviance) et donc une baisse de la vraisemblance du modèle, mais cela est compensé par la réduction du nombre de degrés de liberté.
Le processus est maintenant répété. À la seconde étape, supprimer lecture.bd permettrait de diminuer encore l’AIC à 2250,6 et cette variable est supprimée.
À la troisième étape, tout retrait d’une variable additionnelle reviendrait à augmenter l’AIC.
Lors de la seconde étape, toute suppression d’une autre variable ferait augmenter l’AIC. La procédure s’arrête donc.
L’objet mod2 renvoyé par step() est le modèle final.
Call: glm(formula = sport ~ sexe + groupe_ages + etudes, family = binomial,
data = d)
Coefficients:
(Intercept) sexeHomme
-1.2815 0.4234
groupe_ages25-44 ans groupe_ages45-64 ans
-0.3012 -0.9261
groupe_ages65 ans et plus etudesSecondaire
-1.2696 0.9670
etudesTechnique / Professionnel etudesSupérieur
1.0678 1.9955
etudesNon documenté
2.3192
Degrees of Freedom: 1999 Total (i.e. Null); 1991 Residual
Null Deviance: 2617
Residual Deviance: 2233 AIC: 2251On peut effectuer une analyse de variance ou ANOVA pour comparer les deux modèles avec la fonction anova().
Analysis of Deviance Table
Model 1: sport ~ sexe + groupe_ages + etudes + relig + lecture.bd
Model 2: sport ~ sexe + groupe_ages + etudes
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 1985 2227.1
2 1991 2232.6 -6 -5.4597 0.4863Il n’y a pas de différences significatives entre nos deux modèles (p=0,55). Autrement dit, notre second modèle explique tout autant de variance que notre premier modèle, tout en étant plus parcimonieux.
Astuce
Une alternative à la fonction step() est la fonction MASS::stepAIC() du package MASS qui fonctionne de la même manière. Si cela ne change rien aux régressions logistiques classiques, il arrive que pour certains types de modèle la méthode step() ne soit pas disponible, mais que MASS::stepAIC() puisse être utilisée à la place.
Attachement du package : 'MASS'L'objet suivant est masqué depuis 'package:gtsummary':
selectL'objet suivant est masqué depuis 'package:dplyr':
selectStart: AIC=2257.1
sport ~ sexe + groupe_ages + etudes + relig + lecture.bd
Df Deviance AIC
- relig 5 2231.9 2251.9
- lecture.bd 1 2227.9 2255.9
<none> 2227.1 2257.1
- sexe 1 2245.6 2273.6
- groupe_ages 3 2280.1 2304.1
- etudes 4 2375.5 2397.5
Step: AIC=2251.95
sport ~ sexe + groupe_ages + etudes + lecture.bd
Df Deviance AIC
- lecture.bd 1 2232.6 2250.6
<none> 2231.9 2251.9
- sexe 1 2248.8 2266.8
- groupe_ages 3 2282.1 2296.1
- etudes 4 2380.5 2392.5
Step: AIC=2250.56
sport ~ sexe + groupe_ages + etudes
Df Deviance AIC
<none> 2232.6 2250.6
- sexe 1 2249.2 2265.2
- groupe_ages 3 2282.5 2294.5
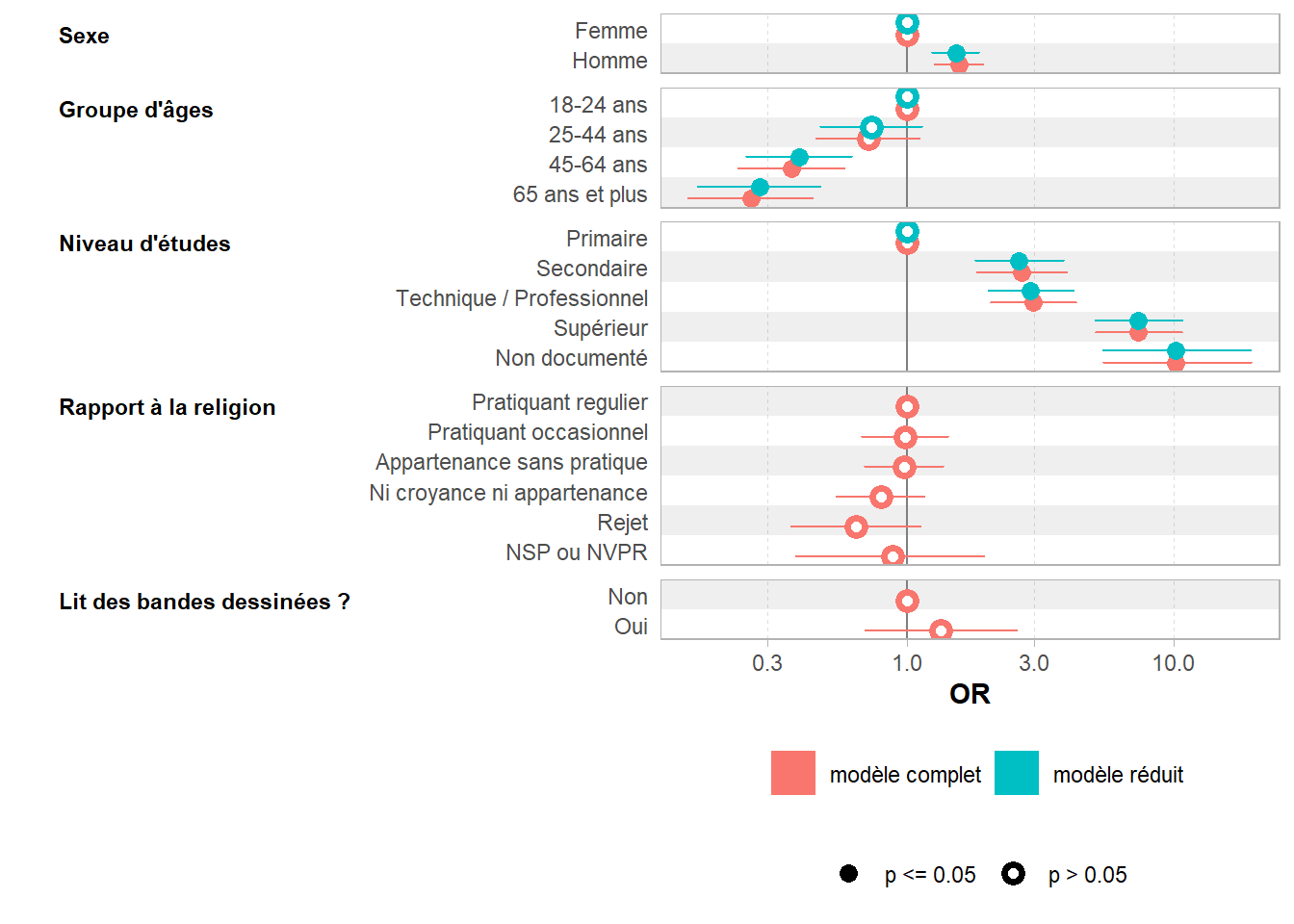
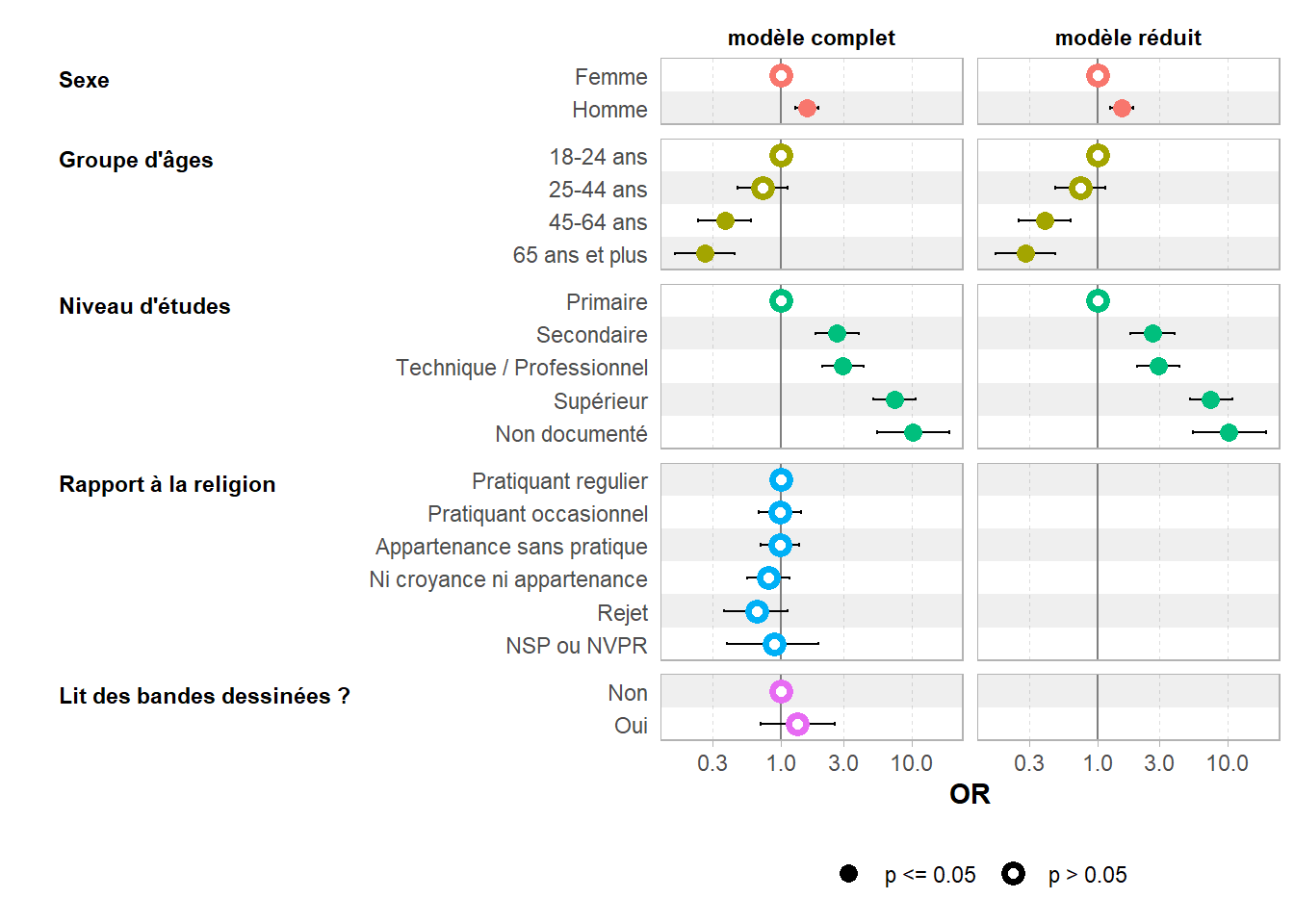
- etudes 4 2385.2 2395.2On peut facilement comparer visuellement deux modèles avec ggstats::ggcoef_compare() de ggstats.
23.4 Sélection pas à pas ascendante
Pour une approche ascendante, nous allons partir d’un modèle vide, c’est-à-dire d’un modèle sans variable explicative avec simplement un intercept.
Nous allons ensuite passer ce modèle vide à step() et préciser, via un élément nommé upper dans une liste passée à l’argument scope, la formule du modèle maximum à considérer. Nous précisons direction = "forward" pour indiquer que nous souhaitons une procédure ascendante.
mod3 <- step(
mod_vide,
direction = "forward",
scope = list(
upper = ~ sexe + groupe_ages + etudes + relig + lecture.bd
)
)Start: AIC=2619.11
sport ~ 1
Df Deviance AIC
+ etudes 4 2294.9 2304.9
+ groupe_ages 3 2405.4 2413.4
+ sexe 1 2600.2 2604.2
+ lecture.bd 1 2612.7 2616.7
<none> 2617.1 2619.1
+ relig 5 2608.8 2620.8
Step: AIC=2304.92
sport ~ etudes
Df Deviance AIC
+ groupe_ages 3 2249.2 2265.2
+ sexe 1 2282.5 2294.5
<none> 2294.9 2304.9
+ lecture.bd 1 2294.7 2306.7
+ relig 5 2293.0 2313.0
Step: AIC=2265.17
sport ~ etudes + groupe_ages
Df Deviance AIC
+ sexe 1 2232.6 2250.6
<none> 2249.2 2265.2
+ lecture.bd 1 2248.8 2266.8
+ relig 5 2246.0 2272.0
Step: AIC=2250.56
sport ~ etudes + groupe_ages + sexe
Df Deviance AIC
<none> 2232.6 2250.6
+ lecture.bd 1 2231.9 2251.9
+ relig 5 2227.9 2255.9Cette fois-ci, à chaque étape, la fonction step() évalue le gain à ajouter chaque variable dans le modèle, ajoute la variable la plus pertinente, pour recommence le processus jusqu’à ce qu’il n’y ait plus de gain à ajouter une variable au modèle. Notons que nous aboutissons ici au même résultat.
Astuce
Nous aurions pu nous passer de préciser direction = "forward". Dans cette situation, step() regarde simultanément les gains à ajouter une variable additionnelle au modèle et à supprimer une variable déjà inclue pour . Lorsque l’on part d’un modèle vide, cela ne change rien au résultat.
mod3 <- step(
mod_vide,
scope = list(
upper = ~ sexe + groupe_ages + etudes + relig + lecture.bd
)
)Start: AIC=2619.11
sport ~ 1
Df Deviance AIC
+ etudes 4 2294.9 2304.9
+ groupe_ages 3 2405.4 2413.4
+ sexe 1 2600.2 2604.2
+ lecture.bd 1 2612.7 2616.7
<none> 2617.1 2619.1
+ relig 5 2608.8 2620.8
Step: AIC=2304.92
sport ~ etudes
Df Deviance AIC
+ groupe_ages 3 2249.2 2265.2
+ sexe 1 2282.5 2294.5
<none> 2294.9 2304.9
+ lecture.bd 1 2294.7 2306.7
+ relig 5 2293.0 2313.0
- etudes 4 2617.1 2619.1
Step: AIC=2265.17
sport ~ etudes + groupe_ages
Df Deviance AIC
+ sexe 1 2232.6 2250.6
<none> 2249.2 2265.2
+ lecture.bd 1 2248.8 2266.8
+ relig 5 2246.0 2272.0
- groupe_ages 3 2294.9 2304.9
- etudes 4 2405.4 2413.4
Step: AIC=2250.56
sport ~ etudes + groupe_ages + sexe
Df Deviance AIC
<none> 2232.6 2250.6
+ lecture.bd 1 2231.9 2251.9
+ relig 5 2227.9 2255.9
- sexe 1 2249.2 2265.2
- groupe_ages 3 2282.5 2294.5
- etudes 4 2385.2 2395.223.5 Forcer certaines variables dans le modèle réduit
Même si l’on a recourt à step(), on peut vouloir forcer la présence de certaines variables dans le modèle, même si leur suppression minimiserait l’AIC. Par exemple, si l’on a des hypothèses spécifiques pour ces variables et que l’on a intérêt à montrer qu’elles n’ont pas d’effet dans le modèle multivariable.
Supposons que nous avons une hypothèse sur le lien entre la pratique d’un sport et la lecture de bandes dessinées. Nous souhaitons donc forcer la présence de la variable lecture.bd dans le modèle final. Cette fois-ci, nous allons indiquer, via la liste passée à scope, un élément lower indiquant le modèle minimum souhaité. Toutes les variables de ce modèle minimum seront donc conserver dans le modèle final.
Start: AIC=2257.1
sport ~ sexe + groupe_ages + etudes + relig + lecture.bd
Df Deviance AIC
- relig 5 2231.9 2251.9
<none> 2227.1 2257.1
- sexe 1 2245.6 2273.6
- groupe_ages 3 2280.1 2304.1
- etudes 4 2375.5 2397.5
Step: AIC=2251.95
sport ~ sexe + groupe_ages + etudes + lecture.bd
Df Deviance AIC
<none> 2231.9 2251.9
- sexe 1 2248.8 2266.8
- groupe_ages 3 2282.1 2296.1
- etudes 4 2380.5 2392.5Cette fois-ci, nous constatons que la fonction step() n’a pas considéré la suppression éventuelle de la variable lecture.bd qui est donc conservée.
23.6 Minimisation du BIC
Un critère similaire à l’AIC est le critère BIC (Bayesian Information Criterion) appelé aussi SBC (Schwarz information criterion).
Sa formule est proche de celle de l’AIC : \(BIC=ln(n)k-2ln(L)\) où \(n\) correspond au nombre d’observations dans l’échantillon. Par rapport à l’AIC, il pénalise donc plus le nombre de degrés de liberté du modèle.
Pour réaliser une sélection pas à pas par optimisation du BIC, on appellera step() en ajoutant l’argument k = log(n) où n est le nombre d’observations inclues dans le modèle. Par défaut, un modèle est calculé en retirant les observations pour lesquelles des données sont manquantes. Dès lors, pour obtenir le nombre exact d’observations incluses dans le modèle, on peut utiliser la syntaxe mod |> model.matrix() |> nrow(), model.matrix() renvoyant la matrice de données ayant servi au calcul du modèle et nrow() le nombre de lignes.
Start: AIC=2341.11
sport ~ sexe + groupe_ages + etudes + relig + lecture.bd
Df Deviance AIC
- relig 5 2231.9 2308.0
- lecture.bd 1 2227.9 2334.3
<none> 2227.1 2341.1
- sexe 1 2245.6 2352.0
- groupe_ages 3 2280.1 2371.3
- etudes 4 2375.5 2459.1
Step: AIC=2307.96
sport ~ sexe + groupe_ages + etudes + lecture.bd
Df Deviance AIC
- lecture.bd 1 2232.6 2301.0
<none> 2231.9 2308.0
- sexe 1 2248.8 2317.2
- groupe_ages 3 2282.1 2335.3
- etudes 4 2380.5 2426.1
Step: AIC=2300.97
sport ~ sexe + groupe_ages + etudes
Df Deviance AIC
<none> 2232.6 2301.0
- sexe 1 2249.2 2310.0
- groupe_ages 3 2282.5 2328.1
- etudes 4 2385.2 2423.223.7 Afficher les indicateurs de performance
Il existe plusieurs indicateurs de performance
ou qualité
d’un modèle. Pour les calculer/afficher (dont l’AIC et le BIC), on pourra avoir recours à broom::glance() ou encore à performance::model_performance().
# A tibble: 1 × 8
null.deviance df.null logLik AIC BIC deviance df.residual nobs
<dbl> <int> <dbl> <dbl> <dbl> <dbl> <int> <int>
1 2617. 1999 -1114. 2257. 2341. 2227. 1985 2000# Indices of model performance
AIC | AICc | BIC | Tjur's R2 | RMSE | Sigma | Log_loss | Score_log | Score_spherical | PCP
-----------------------------------------------------------------------------------------------------------
2257.101 | 2257.343 | 2341.115 | 0.183 | 0.434 | 1.000 | 0.557 | -Inf | 0.001 | 0.623Le fonction performance::compare_performance() permet de comparer rapidement plusieurs modèles.
# Comparison of Model Performance Indices
Name | Model | AIC (weights) | AICc (weights) | BIC (weights) | Tjur's R2 | RMSE | Sigma | Log_loss | Score_log | Score_spherical | PCP
--------------------------------------------------------------------------------------------------------------------------------------------
mod | glm | 2257.1 (0.025) | 2257.3 (0.023) | 2341.1 (<.001) | 0.183 | 0.434 | 1.000 | 0.557 | -Inf | 0.001 | 0.623
mod2 | glm | 2250.6 (0.651) | 2250.7 (0.654) | 2301.0 (0.971) | 0.181 | 0.435 | 1.000 | 0.558 | -Inf | 0.002 | 0.622
mod4 | glm | 2252.0 (0.325) | 2252.1 (0.323) | 2308.0 (0.029) | 0.181 | 0.435 | 1.000 | 0.558 | -Inf | 0.002 | 0.622Si l’on souhaite afficher l’AIC (ainsi que d’autres statistiques globales du modèle) en note du tableau des coefficients, on pourra utiliser gtsummary::add_glance_source_note().
Caractéristique |
OR |
95% IC |
p-valeur |
|---|---|---|---|
| Sexe | |||
| Femme | — | — | |
| Homme | 1,53 | 1,25 – 1,87 | <0,001 |
| Groupe d'âges | |||
| 18-24 ans | — | — | |
| 25-44 ans | 0,74 | 0,48 – 1,15 | 0,2 |
| 45-64 ans | 0,40 | 0,25 – 0,62 | <0,001 |
| 65 ans et plus | 0,28 | 0,17 – 0,47 | <0,001 |
| Niveau d'études | |||
| Primaire | — | — | |
| Secondaire | 2,63 | 1,80 – 3,88 | <0,001 |
| Technique / Professionnel | 2,91 | 2,03 – 4,22 | <0,001 |
| Supérieur | 7,36 | 5,10 – 10,8 | <0,001 |
| Non documenté | 10,2 | 5,43 – 19,4 | <0,001 |
déviance nulle = 2 617; degrés de liberté du modèle nul = 1 999; Log-likelihood = -1 116; AIC = 2 251; BIC = 2 301; Deviance = 2 233; degrés de liberté des résidus = 1 991; No. Obs. = 2 000 |
|||
|
1 OR = rapport de cotes, IC = intervalle de confiance |
|||
23.8 Sélection pas à pas et valeurs manquantes
Si certaines de nos variables explications contiennent des valeurs manquantes (NA), cela peut entraîner des erreurs au moment d’avoir recours à step(), car le nombre d’observations dans le modèle va changer si on retire du modèle une variable explicative avec des valeurs manquantes.
Prenons un exemple, en ajoutant des valeurs manquantes à la variable relig (pour cela nous allons recoder les refus et les ne sait pas en NA).
Au moment d’exécuter step() nous obtenons l’erreur mentionnée précédemment.
Start: AIC=2096.64
sport ~ sexe + groupe_ages + etudes + relig_na + lecture.bd
Df Deviance AIC
- relig_na 3 2073.2 2093.2
- lecture.bd 1 2072.2 2096.2
<none> 2070.6 2096.6
- sexe 1 2088.6 2112.6
- groupe_ages 3 2118.0 2138.0
- etudes 4 2218.1 2236.1Error in step(mod_na): le nombre de lignes utilisées a changé : supprimer les valeurs manquantes ?Pas d’inquiétude ! Il y a moyen de s’en sortir en adoptant la stratégie suivante :
- créer une copie du jeu de données avec uniquement des observations sans valeur manquante pour nos variables explicatives ;
- calculer notre modèle complet à partir de ce jeu de données ;
- appliquer
step(); - recalculer le modèle réduit en repartant du jeu de données complet.
Première étape, ne garder que les observations complètes à l’aide de tidyr::drop_na(), en lui indiquant la liste des variables dans lesquelles vérifier la présence ou non de NA.
Deuxième étape, calculons le modèle complet avec ce jeu données.
Le modèle mod_na_alt est tout à fait identique au modèle mod_na, car glm() supprime de lui-même les valeurs manquantes quand elles existent. Nous pouvons maintenant utiliser step().
Start: AIC=2096.64
sport ~ sexe + groupe_ages + etudes + relig_na + lecture.bd
Df Deviance AIC
- relig_na 3 2073.2 2093.2
- lecture.bd 1 2072.2 2096.2
<none> 2070.6 2096.6
- sexe 1 2088.6 2112.6
- groupe_ages 3 2118.0 2138.0
- etudes 4 2218.1 2236.1
Step: AIC=2093.19
sport ~ sexe + groupe_ages + etudes + lecture.bd
Df Deviance AIC
- lecture.bd 1 2074.6 2092.6
<none> 2073.2 2093.2
- sexe 1 2090.2 2108.2
- groupe_ages 3 2118.5 2132.5
- etudes 4 2221.4 2233.4
Step: AIC=2092.59
sport ~ sexe + groupe_ages + etudes
Df Deviance AIC
<none> 2074.6 2092.6
- sexe 1 2091.1 2107.1
- groupe_ages 3 2119.6 2131.6
- etudes 4 2227.2 2237.2Cela s’exécute sans problème car tous les sous-modèles sont calculés à partir de d_complet et donc ont bien le même nombre d’observations. Cependant, dans notre modèle réduit, on a retiré 137 observations en raison d’une valeur manquante sur la variable relig_na, variable qui n’est plus présente dans notre modèle réduit. Il serait donc pertinent de réintégrer ces observations.
Nous allons donc recalculer le modèle réduit mais à partir de d. Inutile de recopier à la main la formule du modèle réduit, car nous pouvons l’obtenir directement avec mod_na_reduit$formula.
Attention : mod_na_reduit et mod_na_reduit2 ne sont pas identiques puisque le second a été calculé sur un plus grand nombre d’observations, ce qui change très légèrement les valeurs des coefficients.
Astuce
Pour automatiser l’ensemble de ce processus, on peut copier/coller le code de la fonction générique suivante1 :
step_with_na <- function(model,
full_data = eval(model$call$data),
...) {
# data with no NAs
if (is.null(full_data)) {
...data_no_na <- model.frame(model)
} else {
...data_no_na <- get_all_vars(model, data = full_data) |> na.omit()
}
# assign ...data_no_na in parent.frame()
assign("...data_no_na", ...data_no_na, envir = parent.frame())
# refit the model without NAs
model_no_na <- update(
model,
formula = terms(model),
data = ...data_no_na
)
# apply step()
model_simplified <- step(model_no_na, ...)
# recompute simplified model using full data
if (is.null(full_data)) {
update(
model,
formula = terms(model_simplified)
)
} else {
update(
model,
formula = terms(model_simplified),
data = full_data
)
}
}Elle réalise l’ensemble des opérations décrites plus haut en profitant de la flexibilité offerte par la fonction update(). La fonction terms() permet de récupérer l’équation du modèle. La fonction model.frame() permet de récupérer le jeu de données utilisé par un modèle (et dans lequel les lignes incomplètes ont été supprimées), mais cela ne marchera que si c’est un modèle simple (chaque terme du modèle est une variable directe du tableau de données et non une variable calculée). Sinon, on peut appeler step_with_na() en lui passant en plus le tableau de données original. Cela permet d’avoir recours à la fonction get_all_vars() qui permet d’extraire d’un tableau de données toutes les variables nécessaires au calcul d’un modèle.
Attention : il s’agit d’une fonction expérimentale et elle n’est peut-être pas compatible avec tous les types de modèles. Elle a été testée avec les modèles lm(), glm() et nnet::multinom().
Le résultat obtenu est strictement identique.
1 L’argument full_data peut-être utile lorsque le jeu de données n’est pas disponible dans l’environnement parent, par exemple lorsque l’on imbrique des calculs avec lapply() ou purrr:map(). On pourra lors passer manuellement le jeu de données complet à la fonction.