40 Classification ascendante hiérarchique
Il existe de nombreuses techniques statistiques visant à partinionner une population en différentes classes ou sous-groupes. La classification ascendante hiérarchique (CAH) est l’une d’entre elles. On cherche à ce que les individus regroupés au sein d’une même classe (homogénéité intra-classe) soient le plus semblables possibles tandis que les classes soient le plus dissemblables (hétérogénéité inter-classe).
Le principe de la CAH est de rassembler des individus selon un critère de ressemblance défini au préalable qui s’exprimera sous la forme d’une matrice de distances, exprimant la distance existant entre chaque individu pris deux à deux. Deux observations identiques auront une distance nulle. Plus les deux observations seront dissemblables, plus la distance sera importante. La CAH va ensuite rassembler les individus de manière itérative afin de produire un dendrogramme ou arbre de classification. La classification est ascendante car elle part des observations individuelles ; elle est hiérarchique car elle produit des classes ou groupes de plus en plus vastes, incluant des sous-groupes en leur sein. En découpant cet arbre à une certaine hauteur choisie, on produira la partition désirée.
40.1 Calculer une matrice des distances
La notion de ressemblance entre observations est évaluée par une distance entre individus. Plusieurs type de distances existent selon les données utilisées.
Il existe de nombreuses distances mathématiques pour les variables quantitatives (euclidiennes, Manhattan…) que nous n’aborderons pas ici1. La plupart peuvent être calculées avec la fonction stats::dist().
1 Pour une présentation des propriétés mathématiques des distances et des distances les lus courantes, on pourra se référer à la page Wikipedia correspondance.
2 Cette même fonction peut aussi être utilisée pour calculer une distance après une analyse en composantes principales ou une analyse mixte de Hill et Smith.
Usuellement, pour un ensemble de variables qualitatives, on aura recours à la distance du Φ² qui est celle utilisée pour l’analyse des correspondances multiples (cf. Chapitre 39). Avec l’extension ade4, la distance du Φ² s’obtient avec la fonction ade4::dist.dudi()2. Le cas particulier de la CAH avec l’extension FactoMineR sera abordée un peu plus loin.
Nous évoquerons également la distance de Gower qui peut s’appliquer à un ensemble de variables à la fois qualitatives et quantitatives et qui se calcule avec la fonction cluster::daisy() de l’extension cluster.
Il existe bien entendu d’autres types de distance. Par exemple, dans le chapitre sur l’analyse de séquences, nous verrons comment calculer une distance entre séquences, permettant ainsi de réaliser une classification ascendante hiérarchique.
40.1.1 Distance de Gower
En 1971, Gower a proposé un indice de similarité qui porte son nom3. L’objectif de cet indice consiste à mesurer dans quelle mesure deux individus sont semblables. L’indice de Gower varie entre 0 et 1. Si l’indice vaut 1, les deux individus sont identiques. À l’opposé, s’il vaut 0, les deux individus considérés n’ont pas de point commun. Si l’on note \(S_g\) l’indice de similarité de Gower, la distance de Gower \(D_g\) s’obtient simplement de la manière suivante : \(D_g = 1 - S_g\). Ainsi, la distance sera nulle entre deux individus identiques et elle sera égale à 1 entre deux individus totalement différents. Cette distance s’obtient sous R avec la fonction cluster::daisy() du package cluster.
3 Voir Gower, J. (1971). A General Coefficient of Similarity and Some of Its Properties. Biometrics, 27(4), 857-871. doi:10.2307/2528823 (http://www.jstor.org/stable/2528823).
L’indice de similarité de Gower entre deux individus x1 et x2 se calcule de la manière suivante :
\[ S_{g}(x_{1},x_{2})=\frac{1}{p}\sum_{j=1}^{p}s_{12j} \]
\(p\) représente le nombre total de caractères (ou de variables) descriptifs utilisés pour comparer les deux individus4. \(s_{ 12j}\) représente la similarité partielle entre les individus 1 et 2 concernant le descripteur \(j\). Cette similarité partielle se calcule différemment s’il s’agit d’une variable qualitative ou quantitative :
4 Pour une description mathématique plus détaillée de cette fonction, notamment en cas de valeur manquante, se référer à l’article original de Gower précédemment cité.
- variable qualitative : \(s_{ 12j}\) vaut 1 si la variable \(j\) prend la même valeur pour les individus 1 et 2, et vaut 0 sinon. Par exemple, si 1 et 2 sont tous les deux « grand », alors \(s_{12j}\) vaudra 1. Si 1 est « grand » et 2 « petit », \(s_{12j}\) vaudra 0.
- variable quantitative : la différence absolue entre les valeurs des deux variables est tout d’abord calculée, soit \(|y_{1j} - y_{2j}|\). Puis l’écart maximum observé sur l’ensemble du fichier est déterminé et noté \(R_j\). Dès lors, la similarité partielle vaut \(s_{12j} = 1 - |y_{1j} - y_{2j}| / R_j\).
Dans le cas où l’on n’a que des variables qualitatives, la valeur de l’indice de Gower correspond à la proportion de caractères en commun. Supposons des individus 1 et 2 décris ainsi :
- homme / grand / blond / étudiant / urbain
- femme / grande / brune / étudiante / rurale
Sur les 5 variables utilisées pour les décrire, 1 et 2 ont deux caractéristiques communes : ils sont grand(e)s et étudiant(e)s. Dès lors, l’indice de similarité de Gower entre 1 et 2 vaut 2/5 = 0,4 (soit une distance de 1 − 0,4 = 0,6).
Plusieurs approches peuvent être retenues pour traiter les valeurs manquantes :
- supprimer tout individu n’étant pas renseigné pour toutes les variables de l’analyse ;
- considérer les valeurs manquantes comme une modalité en tant que telle ;
- garder les valeurs manquantes en tant que valeurs manquantes.
Le choix retenu modifiera les distances de Gower calculées. Supposons que l’on ait :
- homme / grand / blond / étudiant / urbain
- femme / grande / brune / étudiante / manquant
Si l’on supprime les individus ayant des valeurs manquantes, 2 est retirée du fichier d’observations et aucune distance n’est calculée.
Si l’on traite les valeurs manquantes comme une modalité particulière, 1 et 2 partagent alors 2 caractères sur les 5 analysés, la distance de Gower entre eux est alors de 1 − 2/5 =1 − 0,4 = 0,6.
Si on garde les valeurs manquantes, l’indice de Gower est dès lors calculé sur les seuls descripteurs renseignés à la fois pour 1 et 2. La distance de Gower sera calculée dans le cas présent uniquement sur les 4 caractères renseignés et vaudra 1 − 2/4 = 0,5.
40.1.2 Distance du Φ²
Il s’agit de la distance utilisée dans les analyses de correspondance multiples (ACM). C’est une variante de la distance du χ². Nous considérons ici que nous avons Q questions (soit Q variables initiales de type facteur). À chaque individu est associé un patron c’est-à-dire une certaine combinaison de réponses aux Q questions. La distance entre deux individus correspond à la distance entre leurs deux patrons. Si les deux individus présentent le même patron, leur distance sera nulle. La distance du Φ² peut s’exprimer ainsi :
\[ d_{\Phi^2}^2(L_i,L_j)=\frac{1}{Q}\sum_{k}\frac{(\delta_{ik}-\delta_{jk})^2}{f_k} \]
où \(L_i\) et \(L_j\) sont deux patrons, \(Q\) le nombre total de questions. \(\delta_{ik}\) vaut 1 si la modalité \(k\) est présente dans le patron \(L_i\), 0 sinon. \(f_k\)est la fréquence de la modalité \(k\) dans l’ensemble de la population.
Exprimé plus simplement, on fait la somme de l’inverse des fréquences des modalités non communes aux deux patrons, puis on divise par le nombre total de question. Si nous reprenons notre exemple précédent :
- homme / grand / blond / étudiant / urbain
- femme / grande / brune / étudiante / rurale
Pour calculer la distance entre 1 et 2, il nous faut connaître la proportion des différentes modalités dans l’ensemble de la population étudiée. En l’occurrence :
- hommes : 52 % / femmes : 48 %
- grand : 30 % / moyen : 45 % / petit : 25 %
- blond : 15 % / châtain : 45 % / brun : 30 % / blanc : 10 %
- étudiant : 20 % / salariés : 65 % / retraités : 15 %
- urbain : 80 % / rural : 20 %
Les modalités non communes entre les profils de 1 et 2 sont : homme, femme, blond, brun, urbain et rural. La distance du Φ² entre 1 et 2 est donc la suivante :
\[ d_{\Phi^2}^2(L_1,L_2)=\frac{1}{5}(\frac{1}{0,52}+\frac{1}{0,48}+\frac{1}{0,15}+\frac{1}{0,30}+\frac{1}{0,80}+\frac{1}{0,20})=4,05 \]
Cette distance, bien que moins intuitive que la distance de Gower évoquée précédemment, est la plus employée pour l’analyse d’enquêtes en sciences sociales. Il faut retenir que la distance entre deux profils est dépendante de la distribution globale de chaque modalité dans la population étudiée. Ainsi, si l’on recalcule les distances entre individus à partir d’un sous-échantillon, le résultat obtenu sera différent. De manière générale, les individus présentant des caractéristiques rares dans la population vont se retrouver éloignés des individus présentant des caractéristiques fortement représentées.
40.1.3 Illustration
Nous allons reprendre l’exemple utilisé au chapitre précédent sur l’analyse factorielle (cf. Chapitre 39) et portant sur les loisirs pratiqués par les répondants à l’enquête histoire de vie de 2003.
Calculons maintenant une matrice de distances. Il s’agit d’une grande matrice carrée, avec autant de lignes et de colonnes que d’observations et indiquant la distance entre chaque individus pris deux à deux.
La distance de Gower se calcule avec cluster::daisy().
Pour la distance du Φ², nous allons d’abord réaliser une ACM avec ade4::dudi.cm() puis appeler ade4::dist.dudi().
La distance du Φ² peut être calculée entre les observations (ce que nous venons de faire) afin de créer ensuite une typologie d’individus, mais il est également possible de calculer une distance du Φ² entre les modalités des variables afin de créer une typologie de variables. Dans ce cas-là, on appellera ade4::dist.dudi() avec l’option amongrow = FALSE.
40.2 Calcul du dendrogramme
Il faut ensuite choisir une méthode d’agrégation pour construire le dendrogramme. De nombreuses solutions existent (saut minimum, distance maximum, moyenne, méthode de Ward…). Chacune d’elle produira un dendrogramme différent. Nous ne détaillerons pas ici ces différentes techniques5.
5 Les méthodes single, complete, centroid, average et Ward sont présentées succinctement dans le document Hierarchical Clustering par Fatih Karabiber.
6 Ward, J. (1963). Hierarchical Grouping to Optimize an Objective Function. Journal of the American Statistical Association, 58(301), 236-244. doi:10.2307/2282967. (http://www.jstor.org/stable/2282967)
7 Voir par exemple la discussion, en anglais, sur Wikipedia concernant la page présentant la méthode Ward : https://en.wikipedia.org/wiki/Talk:Ward%27s_method
Cependant, à l’usage, on privilégiera le plus souvent la méthode de Ward6. De manière simplifiée, cette méthode cherche à minimiser l’inertie intra-classe et à maximiser l’inertie inter-classe afin d’obtenir des classes les plus homogènes possibles. Cette méthode est souvent incorrectement présentée comme une méthode de minimisation de la variance
alors qu’au sens strict Ward vise l’augmentation minimum de la somme des carrés
(“minimum increase of sum-of-squares (of errors)”)7.
En raison de la variété des distances possibles et de la variété des techniques d’agrégation, on pourra être amené à réaliser plusieurs dendrogrammes différents sur un même jeu de données jusqu’à obtenir une classification qui fait « sens ».
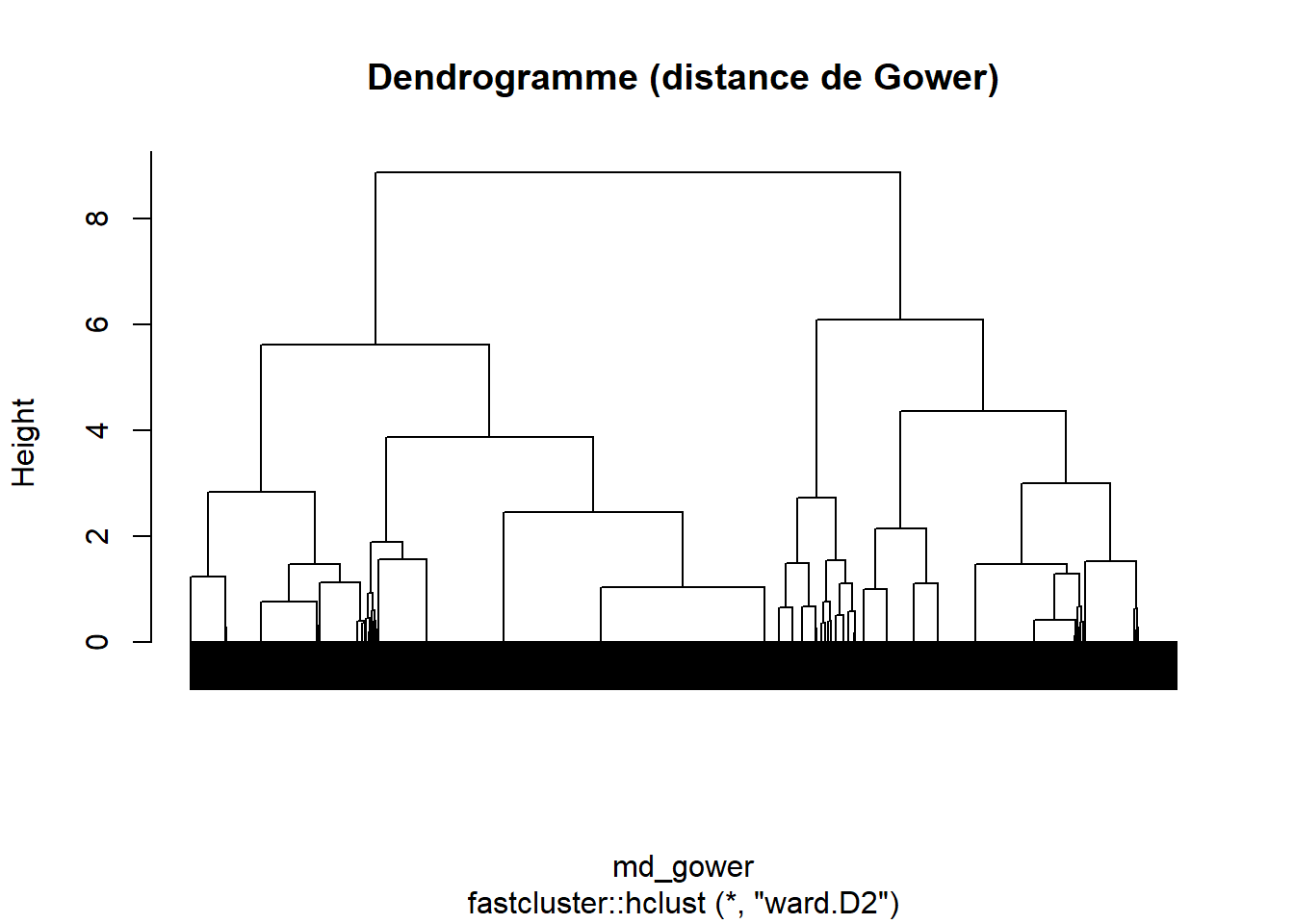
La fonction de base pour le calcul d’un dendrogramme est stats::hclust() en précisant le critère d’agrégation avec method. Dans notre cas, nous allons opter pour la méthode de Ward appliquée au carré des distances (ce qu’on indique avec method = "ward.D2"8) :
8 L’option method = "ward.D" correspondant à la méthode de Ward sur la matrice des distances simples (i.e. sans la passer au carré
). Mais il est à noter que la méthode décrite par Ward dans son article de 1963 correspond bien à method = "ward.D2".
Le temps de calcul d’un dendrogramme peut être particulièrement important sur un gros fichier de données. Le package fastcluster permet de réduire significativement ce temps de calcul. Elle propose une version optimisée de hclust() (les arguments sont identiques).
Il suffira donc de charger fastcluster pour surcharger la fonction hclust(), ou bien d’appeler explicitement fastcluster::hclust().
Le dendrogramme peut également être calculé avec la fonction cluster::agnes(). Cependant, à l’usage, le temps de calcul peut être plus long qu’avec hclust().
Les noms des arguments sont légèrement différents. Pour la méthode de Ward appliquée au carré de la matrice des distance, on précisera à cluster::agnes() l’option method = "ward".
Le résultat obtenu n’est pas au même format que celui de stats::hclust(). Il est possible de transformer un objet cluster::agnes() au format stats::hclust() avec cluster::as.hclust().
40.2.1 Représentation graphique du dendrogramme
Pour une représentation graphique rapide du dendrogramme, on peut directement plot(). Lorsque le nombre d’individus est important, il peut être utile de ne pas afficher les étiquettes des individus avec labels = FALSE.
Pour une représentation graphique un peu plus propre (et avec plus d’options que nous verrons plus loin), nous pouvons avoir recours à factoextra::fviz_dend() du package factoextra. Le temps de calcul du graphique est par contre sensible plus long.
arbre_gower |>
factoextra::fviz_dend(show_labels = FALSE) +
ggplot2::ggtitle("Dendrogramme (distance de Gower)")
Il existe d’autres packages offrant des visualisations avancées pour les dendrogrammes. Citons notamment le package ggdendro et surtout dendextend qui est très complet.
40.3 Découper le dendrogramme
Pour obtenir une partition de la population, il suffit de découper le dendrogramme obtenu à une certaine hauteur. Cela aura pour effet de découper l’échantillon en plusieurs groupes, i.e. en plusieurs classes.
40.3.1 Classes obtenues avec la distance de Gower
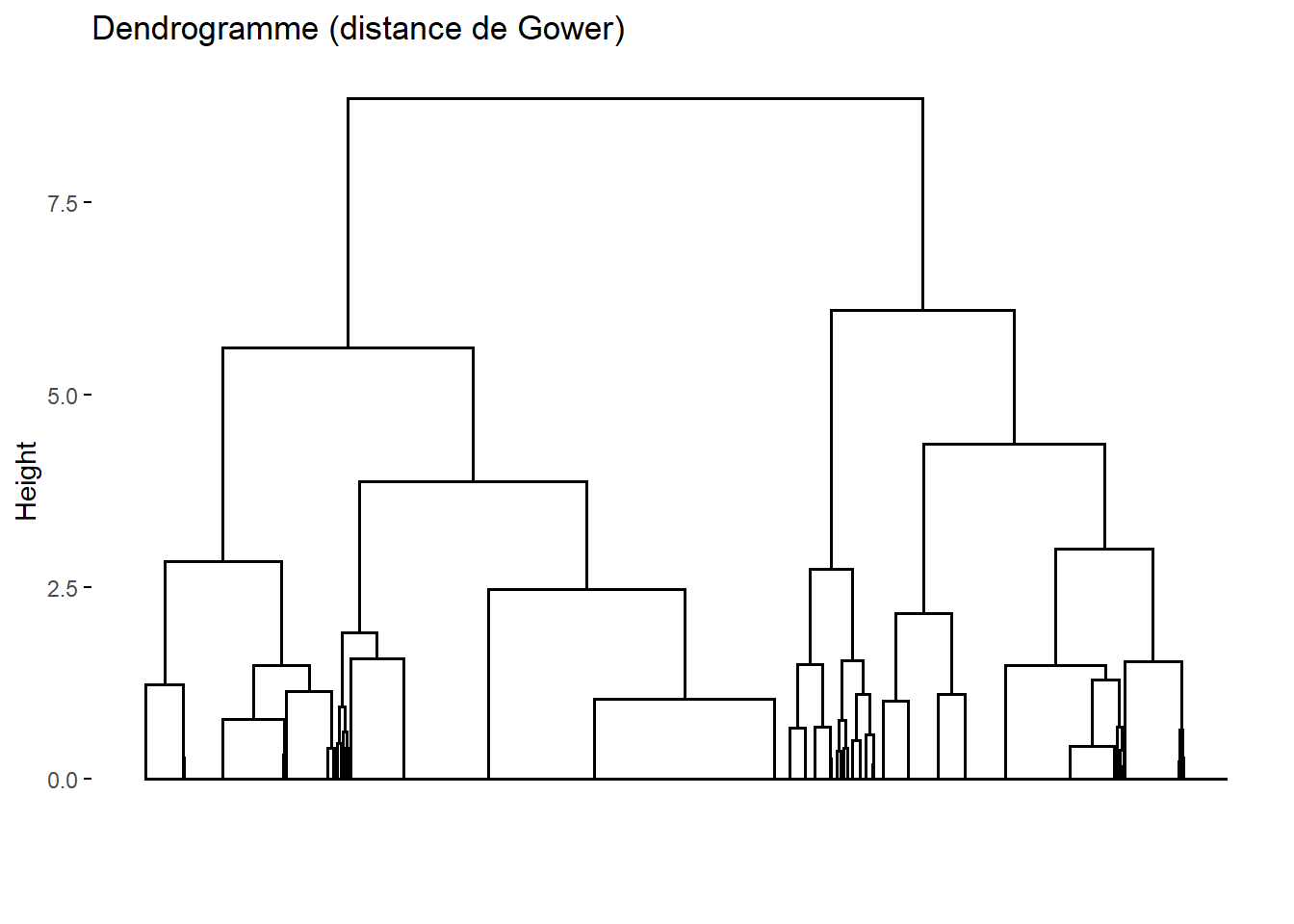
En premier lieu, il est toujours bon de prendre le temps d’observer de la forme des branches du dendrogramme. Reprenons le dendrogramme obtenu avec la distance de Gower (Figure 40.2). Nous recherchons des branches qui se distinguent clairement
, c’est-à-dire avec un saut
marqué sous la branche. Ici, nous avons tout d’abord deux groupes bien distincts qui apparaissent. Chacune des deux premières branches se sépare ensuite en deux branches bien visibles, suggérant une possible classification en 4 groupes.
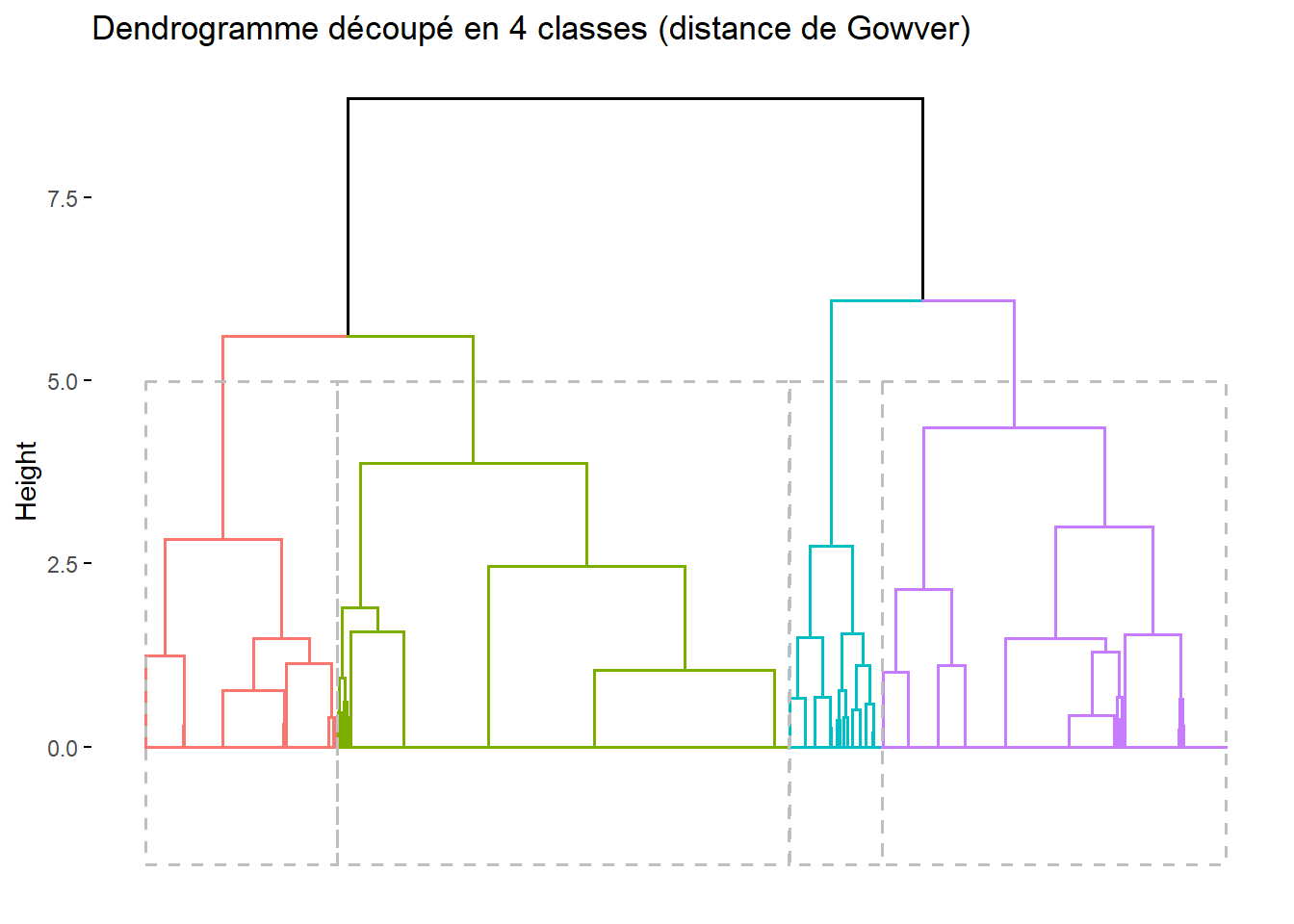
Nous pouvons l’impact d’un découpage avec factoextra::fviz_dend() en précisant k = 4 pour lui indiquer de colorer un découpage en 4 classes. On peut optionnellement ajouter rect = TRUE pour dessiner des rectangles autour de chaque classe.
arbre_gower |>
factoextra::fviz_dend(
show_labels = FALSE,
k = 4,
rect = TRUE
) +
ggplot2::ggtitle("Dendrogramme découpé en 4 classes (distance de Gowver)")
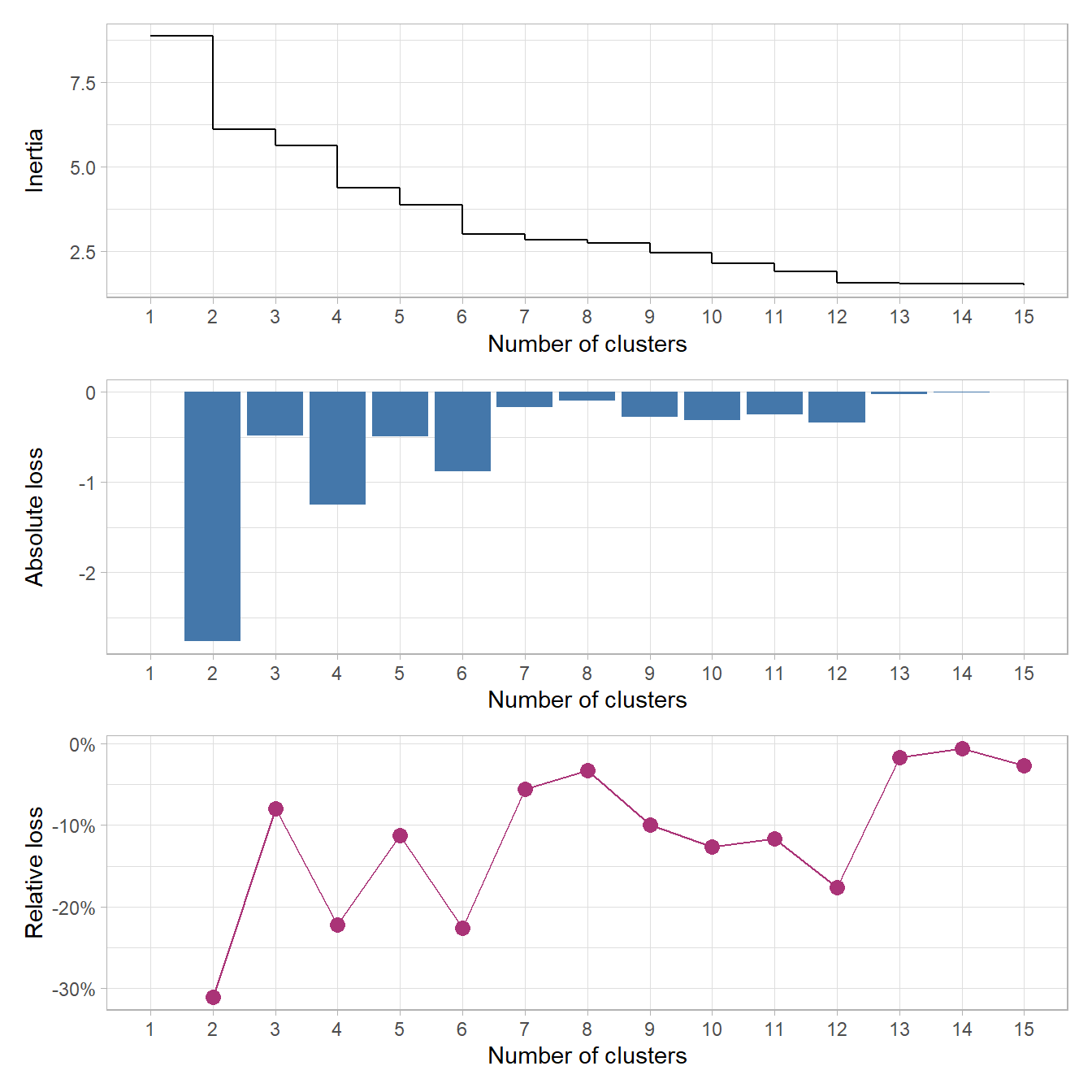
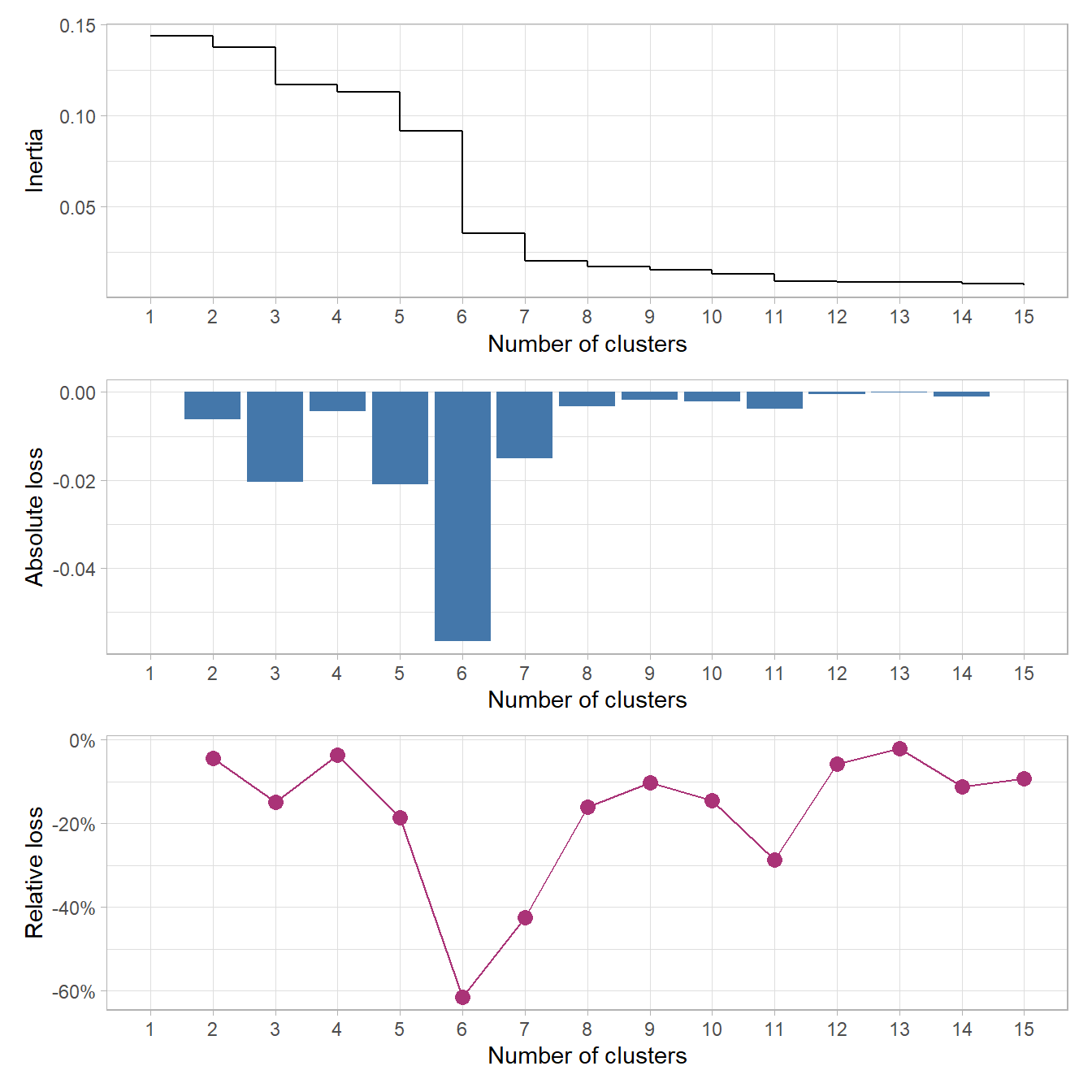
Pour nous aider dans l’analyse du dendrogramme, il est possible de représenter graphiquement les sauts d’inertie (i.e. de la hauteur des branches) au fur-et-à-mesure que l’on découpe l’arbre en un nombre de classes plus important. Nous pouvons également considérer la perte absolue d’inertie (l’écart de hauteur entre le découpage précédent et le découpage considéré) voire la perte relative (i.e. la perte absolue exprimée en pourcentage de la hauteur précédente). FactoMineR (que nous aborderons un peu plus loin) suggère par défaut la partition correspondant à la plus grande perte relative d’inertie (the one with the higher relative loss of inertia).
Pour faciliter les choses, voici deux petites fonctions que vous pouvez recopier / adapter dans vos scripts. get_inertia_from_tree() calcule l’inertie à chaque niveau, ainsi que les pertes absolues et relatives. plot_inertia_from_tree() en propose une représentation graphique.
get_inertia_from_tree <- function(tree, k_max = 15) {
if (inherits(tree, "HCPC"))
tree <- tree$call$t$tree
if (!inherits(tree, "hclust"))
tree <- as.hclust(tree)
inertia <- tree$height |>
sort(decreasing = TRUE) |>
head(k_max)
prev_inertia <- dplyr::lag(inertia)
dplyr::tibble(
k = seq_along(inertia),
inertia = inertia,
absolute_loss = inertia - prev_inertia,
relative_loss = (inertia - prev_inertia) / prev_inertia
)
}
plot_inertia_from_tree <- function(tree, k_max = 15) {
d <- get_inertia_from_tree(tree, k_max)
p_inertia <-
ggplot2::ggplot(d) +
ggplot2::aes(x = k, y = inertia) +
ggplot2::geom_step() +
ggplot2::ylab("Inertia")
p_absolute <-
ggplot2::ggplot(d) +
ggplot2::aes(x = k, y = absolute_loss) +
ggplot2::geom_bar(stat = "identity", fill = "#4477AA") +
ggplot2::ylab("Absolute loss")
p_relative <-
ggplot2::ggplot(d) +
ggplot2::aes(x = k, y = relative_loss) +
ggplot2::geom_line(color = "#AA3377") +
ggplot2::geom_point(size = 3, color = "#AA3377") +
ggplot2::scale_y_continuous(label = scales::percent) +
ggplot2::ylab("Relative loss")
patchwork::wrap_plots(
p_inertia,
p_absolute,
p_relative,
ncol = 1
) &
ggplot2::theme_light() &
ggplot2::xlab("Number of clusters") &
ggplot2::scale_x_continuous(
breaks = d$k,
minor_breaks = NULL,
limits = c(1, k_max)
)
}Voyons ce qu’on obtient.
Dans cet exemple, nous pouvons voir qu’un découpage en deux classes maximise la perte absolue et la perte relative d’inertie. Mais, pour les besoins de l’analyse, nous pouvons souhaiter un nombre de classe un peu plus élevé (plus de classes permet une analyse plus fine, trop de classes rend l’interprétation des résultats compliqués). Un découpage en 4 classes apparaît sur ce graphique comme une bonne alternative, voir un découpage en 6 classes (une lecture du dendrogramme nous permet de voir que, dans cet exemple, un découpage en 6 classes reviendrait à couper en deux les 2 classes les plus larges du découpage en 4 classes).
Pour découper notre dendrogramme et récupérer la classification, nous appliquerons la fonction cutree() au dendrogramme, en indiquant le nombre de classes souhaitées9.
9 Ici, nous pouvons ajouter le résultat obtenu directement à notre tableau de données hdv2003 dans la mesure où, depuis le début de l’analyse, l’ordre des lignes n’a jamais changé à aucune étape de l’analyse.
Nous pouvons rapidement faire un tri à plat avec gtsummary::tbl_summary().
| Caractéristique | N = 2 0001 |
|---|---|
| typo_gower_4classes | |
| 1 | 837 (42%) |
| 2 | 636 (32%) |
| 3 | 172 (8,6%) |
| 4 | 355 (18%) |
| 1 n (%) | |
Nous obtenons deux classes principales regroupant chacune plus du tiers de l’échantillon, une troisième classe regroupant presque un cinquième et une dernière classe avec un peu moins de 9 % des individus.
40.3.2 Classes obtenues à partir de l’ACM (distance du Φ²)
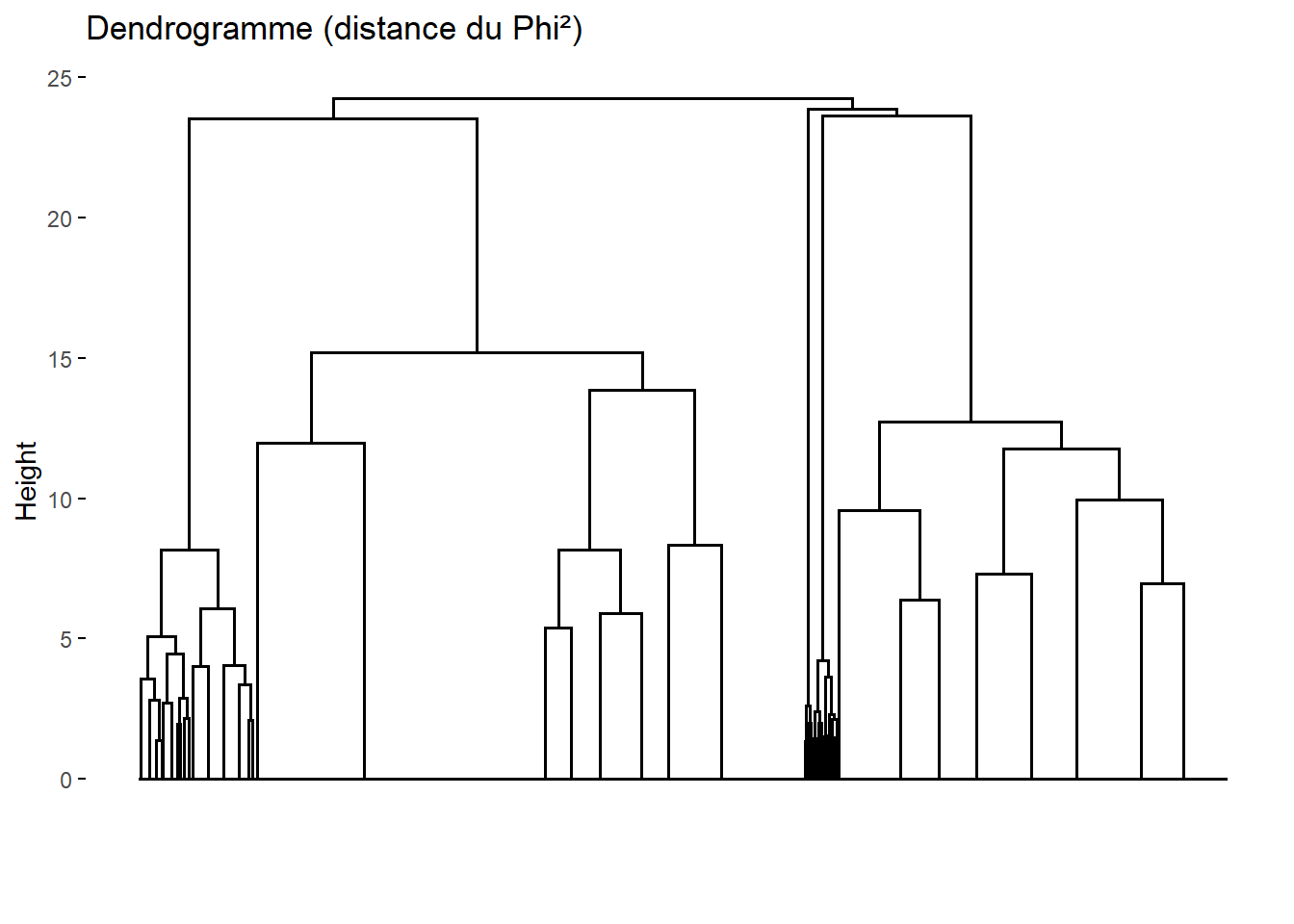
Pour découper l’arbre obtenu à partir de l’ACM, nous allons procéder de la même manière. D’abord, jetons un œil au dendrogramme.
arbre_phi2 |>
factoextra::fviz_dend(show_labels = FALSE) +
ggplot2::ggtitle("Dendrogramme (distance du Phi²)")
Le dendrogramme obtenu est ici bien différent. Cela est lié au fait que les deux distances traitent différemment les modalités atypiques
. En effet, la distance du Φ² prend en compte la fréquence de chaque modalité dans l’ensemble de l’échantillon. De fait, les modalités très peu représentées dans l’échantillon se retrouvent très éloignées des autres et la CAH aura tendance à isoler les individus atypiques. À l’inverse, la distance de Gower est indépendante de la fréquence de chaque modalité dans l’échantillon. De fait, plutôt que d’isoler les individus atypiques, une CAH basée sur la distance de Gower aura plutôt tendance à les associer aux autres à partir de leurs autres caractéristiques, aboutissant à des classes plus équilibrées
.
Il n’y a pas une approche meilleure
que l’autre. Tout dépend des questions de recherche que l’on se posent et de ce que l’on souhaite faire émerger.
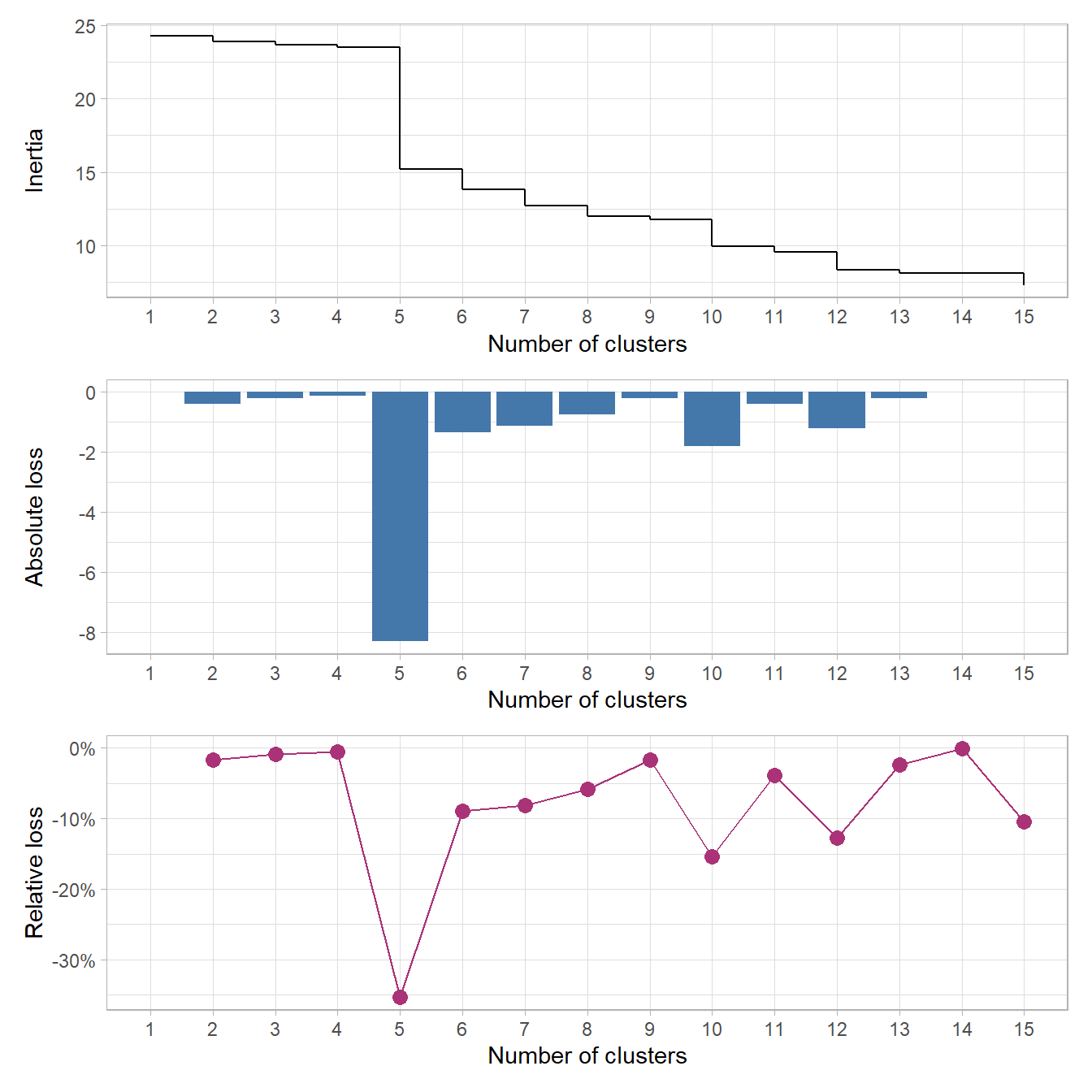
Comme nous pouvons le voir, dès le début du dendrogramme, l’arbre se divise rapidement en 5 branches puis il y a un saut relativement marqué. Nous pouvons confirmer cela avec plot_inertia_from_tree().
Cela confirme un découpage optimal
en 5 classes. Regardons la distribution de cette typologie.
| Caractéristique | N = 2 0001 |
|---|---|
| typo_phi2_5classes | |
| 1 | 1 010 (51%) |
| 2 | 713 (36%) |
| 3 | 216 (11%) |
| 4 | 14 (0,7%) |
| 5 | 47 (2,4%) |
| 1 n (%) | |
Sur les 5 classes, deux sont très atypiques puisqu’elles ne réunissent que 0,7 % et 2,4 % de l’échantillon. À voir si cela est problématique pour la suite de l’analyse. Au besoin, nous pourrions envisager de fusionner les classes 4 et 5 avec la classe 2 avec laquelle elles sont plus proches selon le dendrogramme.
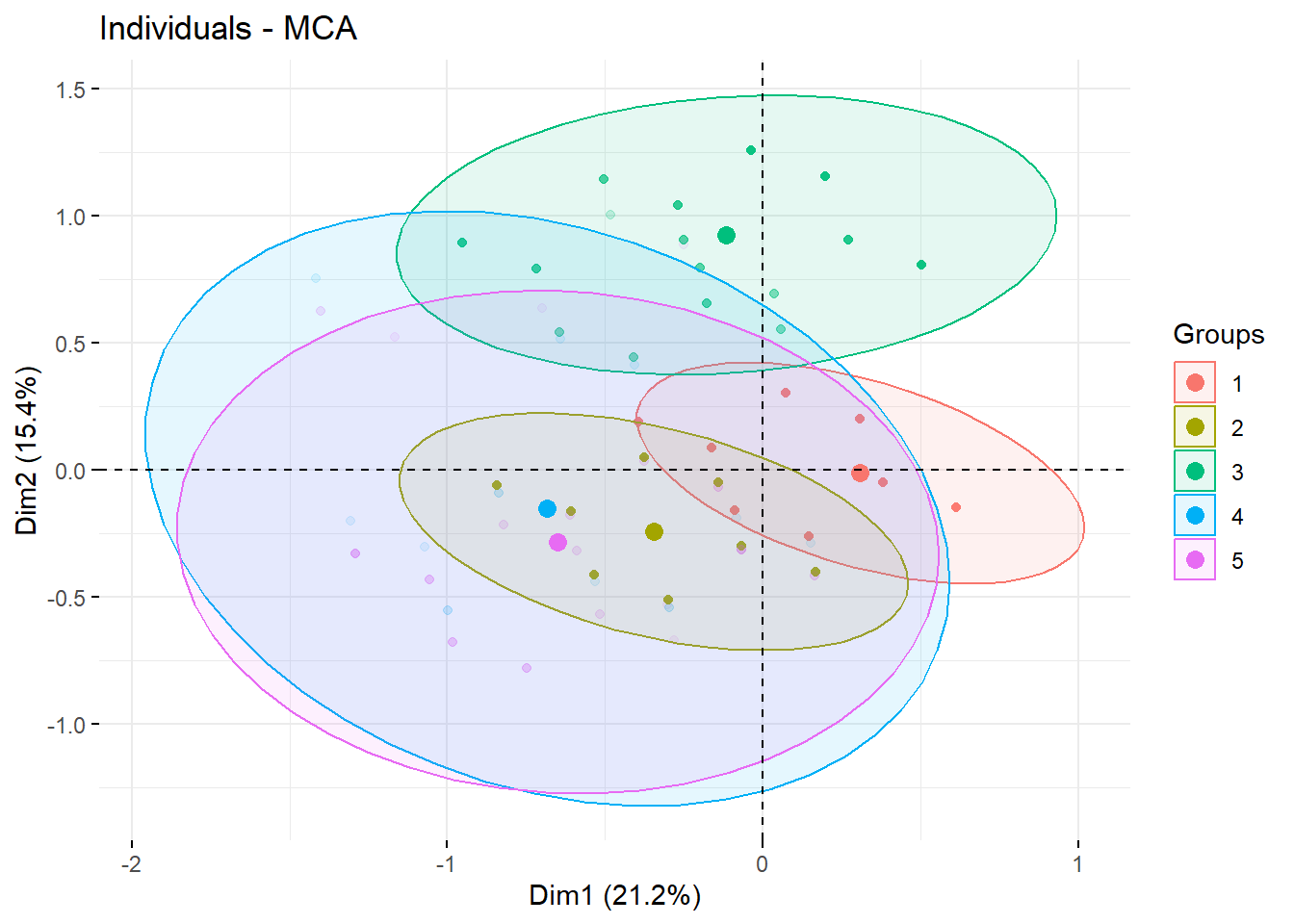
Il est possible de visualiser la répartition de la typologie dans le plan factoriel avec factoextra::fviz_mca_ind() et en passant la typologie à habillage.
acm_ad |>
factoextra::fviz_mca_ind(
habillage = hdv2003$typo_phi2_5classes,
addEllipses = TRUE,
geom.ind = "point",
alpha.ind = 0.1
)
Nous voyons que les classes 1, 2 et 3 séparent bien les individus au niveau du plan factoriel. Les deux classes atypiques 4 et 5, quant à elles, sont diffuses sur les deux premiers axes, suggérant qu’elles capturent des différences observables sur des axes de niveau supérieur.
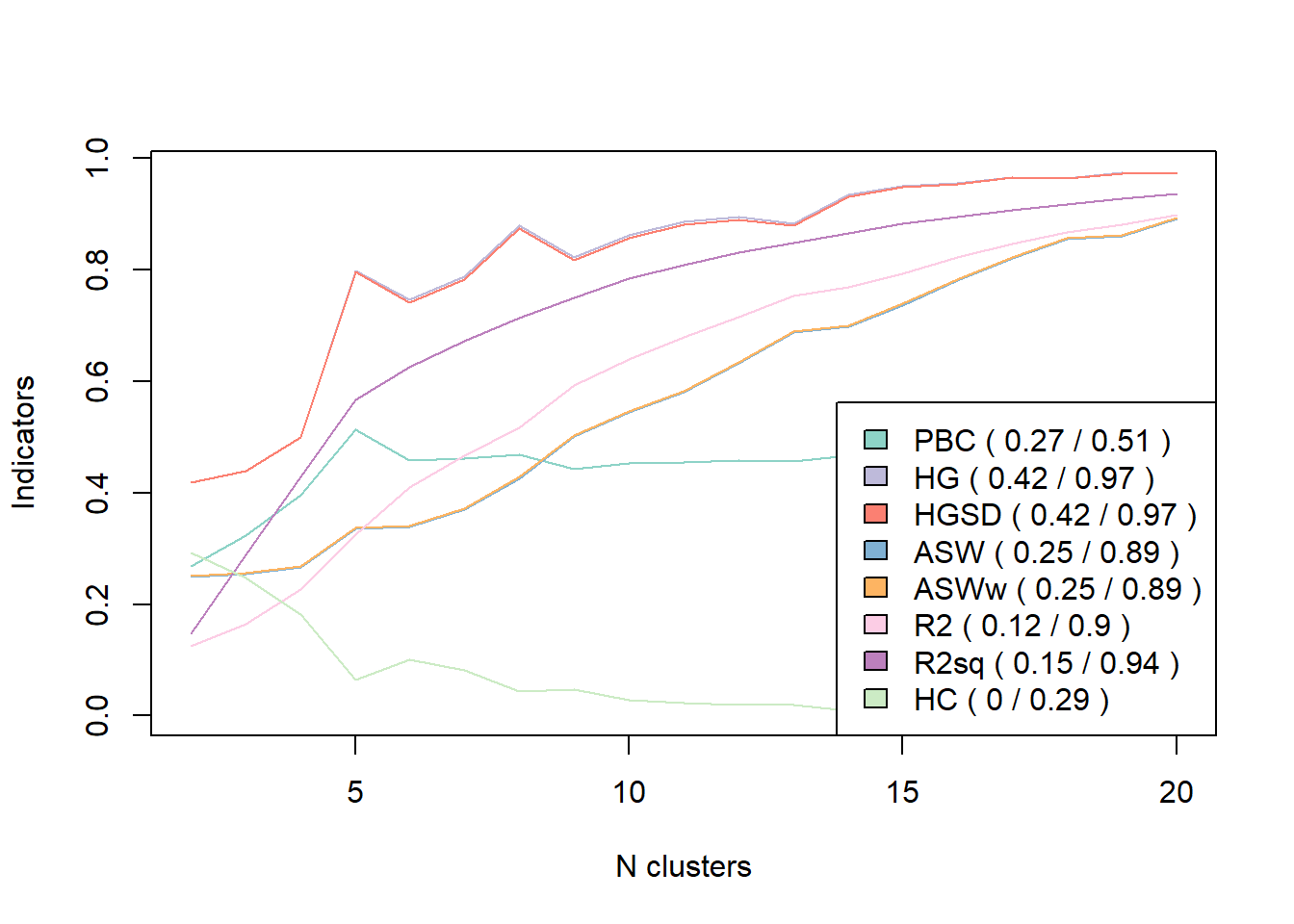
Il existe de multiples autres indicateurs statistiques cherchant à mesurer la qualité
de chaque partition. Pour cela, on pourra par exemple avoir recours à la fonction WeightedCluster::as.clustrange() de l’extension WeightedCluster.
Pour plus d’informations, voir le manuel de la librairie WeightedCluster, chapitre 7.
Registered S3 method overwritten by 'vegan':
method from
rev.hclust dendextend
On pourra également lire Determining The Optimal Number Of Clusters: 3 Must Know Methods par Alboukadel Kassambara, l’un des auteurs du package factoextra.
40.4 Calcul de l’ACM et de la CAH avec FactoMineR
Le package FactoMineR permet lui aussi de réaliser une CAH à partir d’une ACM via la fonction FactoMineR::HCPC() qui réalise les différentes opérations en une seule fois.
FactoMineR::HCPC() réalise à la fois le calcul de la matrice des distances, du dendrogramme et le partitionnement de la population en classes. Par défaut, FactoMineR::HCPC() calcule le dendrogramme à partir du carré des distances du Φ² et avec la méthode de Ward. Si l’on ne précise rien, FactoMineR::HCPC() détermine une partition optimale selon le critère de la plus perte relative d’inertie évoqué plus haut10. La fonction prend en entrée une analyse factorielle réalisée avec FactoMineR. Le paramètre min permet d’indiquer un nombre minimum de classes.
10 Plus précisément si graph = FALSE ou si nb.clust = -1. Si graph = TRUE et nb.clust = 0 (valeurs par défaut), la fonction affichera un dendrogramme interactif et l’utilisateur devra cliquer au niveau de la hauteur où il souhaite réaliser la découpe.
Nous pouvons directement passer le résultat de FactoMineR::HCPC() à factoextra::fviz_dend() pour visualiser le dendrogramme, qui sera d’ailleurs automatiquement colorié à partir de la partition recommandée par FactoMineR::HCPC().
Nous obtenons ici un découpage en 6 classes qui correspond bien à la plus grand perte relative d’inertie comme nous pouvons le vérifier avec plot_inertia_from_tree() qui accepte également en entrée un objet produit par FactoMineR::HCPC().
Par contre, le dendrogramme obtenu diffère de celui que nous avions eu précédemment avec ade4 (cf. Figure 40.5). Cela est dû au fait que FactoMineR::HCPC() procède différemment pour calculer la matrice des distances en ne prenant en compte que les axes retenus dans le cadre de l’ACM.
Pour rappel, par défaut, FactoMineR::MCA() ne retient que les 5 premiers axes de l’espace factoriel. FactoMineR::HCPC() n’a donc pris en compte que ces 5 premiers axes pour calculer les distances entre les individus, considérant que les autres axes n’apportent que du « bruit » rendant la classification instable. Comme le montre summary(acm_fm), nos cinq premiers axes n’expliquent que 78 % de la variance. On considère usuellement préférable de garder un plus grande nombre d’axes afin de couvrir au moins 80 à 90 % de la variance.
De son côté, ade4::dist.dudi() prends en compte l’ensemble des axes pour calculer la matrice des distances. On peut reproduire cela avec FactoMineR en indiquant ncp = Inf lors du calcul de l’ACM.
Nous retrouvons alors le même résultat que celui obtenu avec ade4 et un découpage en 5 classes.
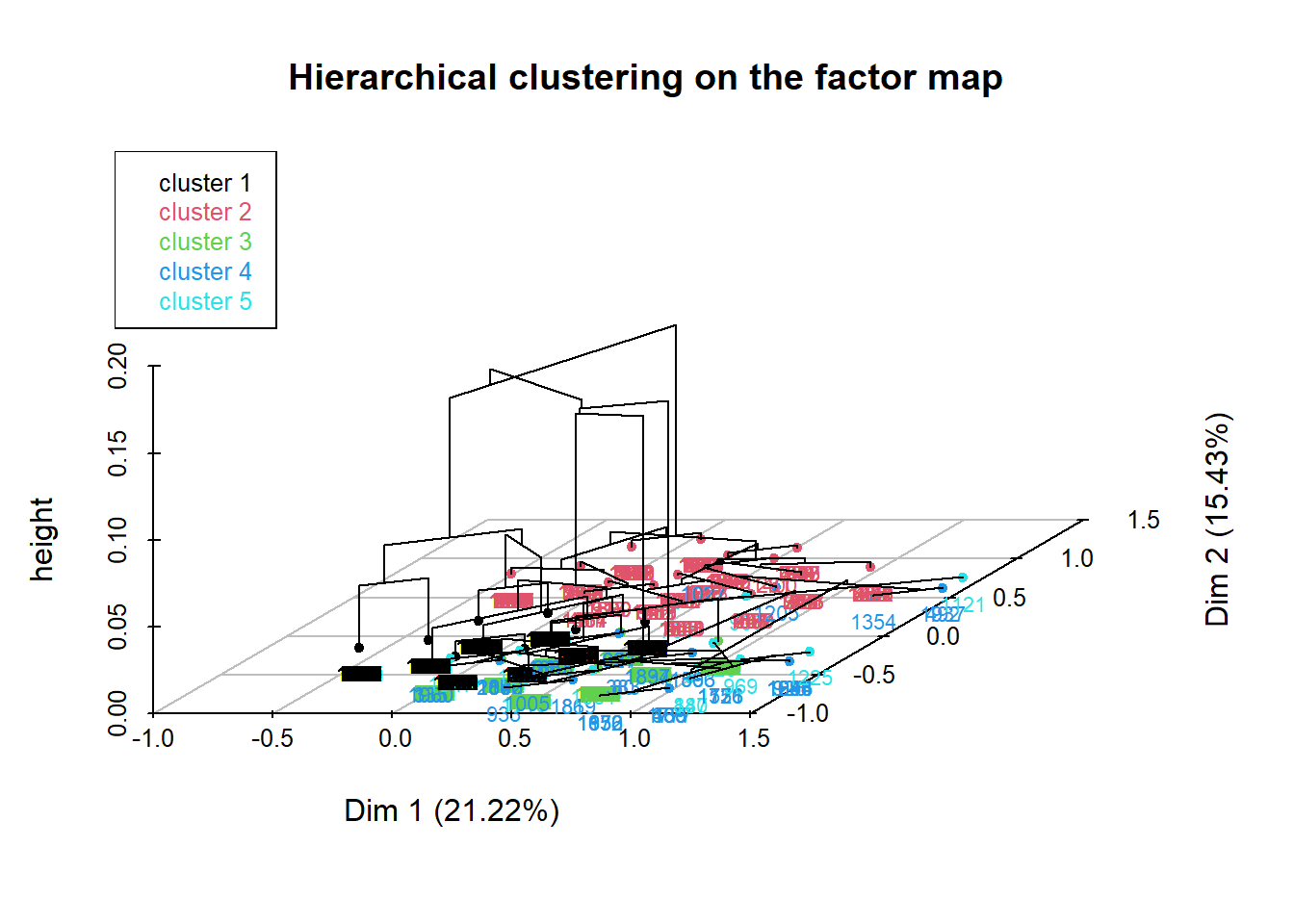
À noter que FactoMineR propose une visualisation en 3 dimensions du dendrogramme projeté sur le plan factoriel.
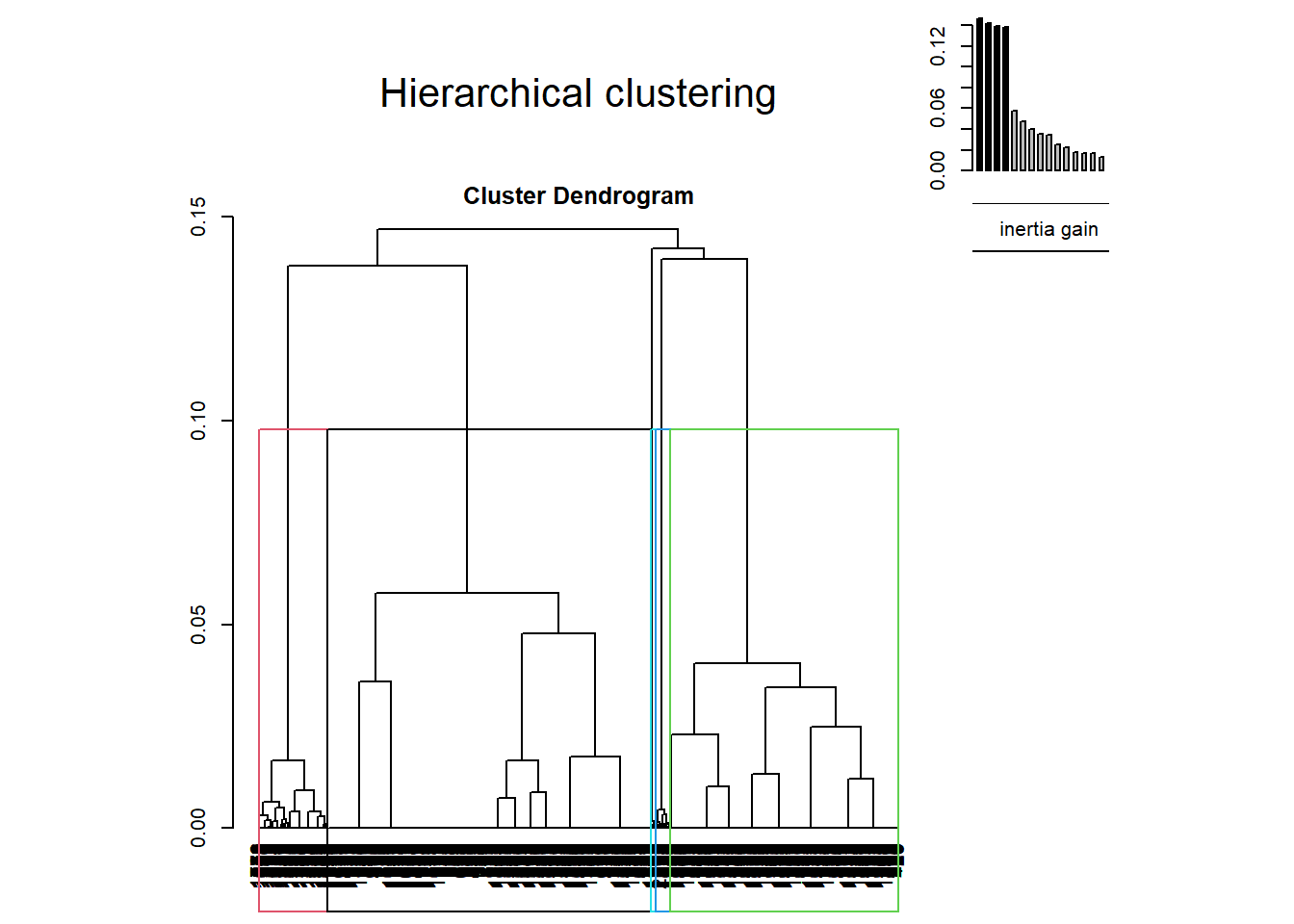
Notons également l’option choice = "tree" qui propose une représentation du dendrogramme, avec des rectangles indiquant le découpage optimal et une vignette présentant l’inertie à chaque découpage.
Pour récupérer la classification, on pourra récupérer la colonne $clust du sous-objet $data.clust du résultat renvoyé par FactoMineR::HCPC().
Si l’on a besoin de découper le dendrogramme à un autre endroit, nous pouvons récupérer le dendrogramme via le sous-objet $call$t$tree puis lui appliquer cutree().
40.5 Caractériser la typologie
Reste le travail le plus important (et parfois le plus difficile) qui consiste à catégoriser la typologie obtenue et le cas échéant à nommer les classes.
En premier lieu, on peut croiser la typologie obtenue avec les différentes variables inclues dans l’ACM. Le plus simple est d’avoir recours à gtsummary::tbl_summary(). Par exemple, pour la typologie obtenue avec la distance de Gower.
| Caractéristique | 1, N = 8371 | 2, N = 6361 | 3, N = 1721 | 4, N = 3551 |
|---|---|---|---|---|
| hard.rock | ||||
| Non | 837 (100%) | 632 (99%) | 171 (99%) | 346 (97%) |
| Oui | 0 (0%) | 4 (0,6%) | 1 (0,6%) | 9 (2,5%) |
| lecture.bd | ||||
| Non | 813 (97%) | 613 (96%) | 172 (100%) | 355 (100%) |
| Oui | 24 (2,9%) | 23 (3,6%) | 0 (0%) | 0 (0%) |
| peche.chasse | ||||
| Non | 806 (96%) | 633 (100%) | 0 (0%) | 337 (95%) |
| Oui | 31 (3,7%) | 3 (0,5%) | 172 (100%) | 18 (5,1%) |
| cuisine | ||||
| Non | 532 (64%) | 316 (50%) | 79 (46%) | 192 (54%) |
| Oui | 305 (36%) | 320 (50%) | 93 (54%) | 163 (46%) |
| bricol | ||||
| Non | 570 (68%) | 317 (50%) | 47 (27%) | 213 (60%) |
| Oui | 267 (32%) | 319 (50%) | 125 (73%) | 142 (40%) |
| cinema | ||||
| Non | 831 (99%) | 226 (36%) | 115 (67%) | 2 (0,6%) |
| Oui | 6 (0,7%) | 410 (64%) | 57 (33%) | 353 (99%) |
| sport | ||||
| Non | 834 (100%) | 2 (0,3%) | 86 (50%) | 355 (100%) |
| Oui | 3 (0,4%) | 634 (100%) | 86 (50%) | 0 (0%) |
| 1 n (%) | ||||
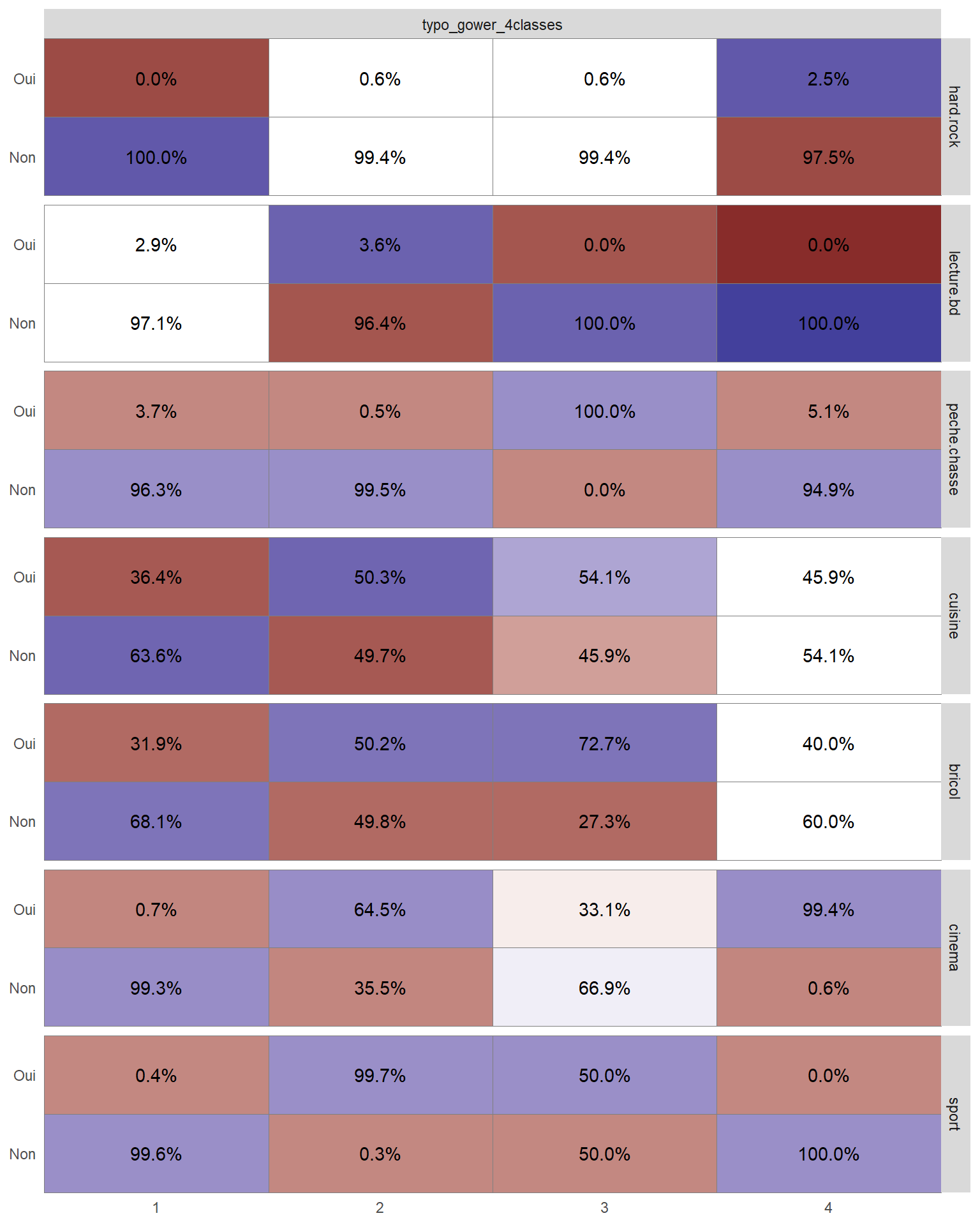
Pour une représentation plus visuelle, on peut également avoir recours à GGally::ggtable() de GGally pour représenter les résidus du Chi² et mieux repérer les différences. La couleur bleue indique que la modalité est sur-représentée et la couleur rouge qu’elle est sous-représentée.
library(GGally)
hdv2003$typo_gower_4classes <- factor(hdv2003$typo_gower_4classes)
ggtable(
hdv2003,
columnsX = "typo_gower_4classes",
columnsY = names(d),
cells = "col.prop",
fill = "std.resid"
) +
labs(fill = "Résidus standardizés du Chi²") +
theme(legend.position = "bottom")
Une première lecture nous indique que :
la première classe rassemble des individus qui n’ont pas (ou peu) de loisirs ;
la seconde classe réunit des personnes pratiquant un sport et ayant souvent une autre activité telle que le cinéma, la bricolage ou la cuisine ;
la troisième classe réunit spécifiquement les individus pratiquant la chasse ou la pêche ;
la quatrième classe correspond à des personnes ne pratiquant pas de sport mais allant au cinéma.
Bien sûr, l’interprétation fine des catégories nécessite un peu plus d’analyse, de croiser avec la littérature et les hypothèses des questions de recherche posées, et de croiser la typologie avec d’autres variables de l’enquête.
Pour la typologie réalisée à partir d’une ACM, nous pourrons procéder de la même manière. Cependant, si la CAH a été réalisée avec FactoMineR::HCPC(), l’objet retourné contient directement un sous-objet $desc.var donnant une description de la typologie obtenue.
Link between the cluster variable and the categorical variables (chi-square test)
=================================================================================
p.value df
hard.rock 0.000000e+00 4
lecture.bd 0.000000e+00 4
peche.chasse 0.000000e+00 4
cinema 0.000000e+00 4
sport 1.122743e-38 4
bricol 4.121835e-11 4
cuisine 8.681152e-04 4
Description of each cluster by the categories
=============================================
$`1`
Cla/Mod Mod/Cla Global p.value v.test
cinema=cinema_Non 86.03066 100.00000 58.70 0.000000e+00 Inf
peche.chasse=peche.chasse_Non 56.86937 100.00000 88.80 2.188843e-75 18.372312
sport=sport_Non 61.39389 77.62376 63.85 6.009360e-39 13.054257
lecture.bd=lecture.bd_Non 51.71531 100.00000 97.65 2.518852e-15 7.912690
bricol=bricol_Non 57.10549 64.85149 57.35 6.993497e-12 6.857788
cuisine=cuisine_Non 54.60232 60.49505 55.95 3.566198e-05 4.133925
hard.rock=hard.rock_Non 50.85599 100.00000 99.30 5.060286e-05 4.052825
hard.rock=hard.rock_Oui 0.00000 0.00000 0.70 5.060286e-05 -4.052825
cuisine=cuisine_Oui 45.28944 39.50495 44.05 3.566198e-05 -4.133925
bricol=bricol_Oui 41.61782 35.14851 42.65 6.993497e-12 -6.857788
lecture.bd=lecture.bd_Oui 0.00000 0.00000 2.35 2.518852e-15 -7.912690
sport=sport_Oui 31.25864 22.37624 36.15 6.009360e-39 -13.054257
peche.chasse=peche.chasse_Oui 0.00000 0.00000 11.20 2.188843e-75 -18.372312
cinema=cinema_Oui 0.00000 0.00000 41.30 0.000000e+00 -Inf
$`2`
Cla/Mod Mod/Cla Global p.value
peche.chasse=peche.chasse_Oui 96.428571 100.00000 11.20 2.257673e-282
bricol=bricol_Oui 14.536928 57.40741 42.65 4.149911e-06
lecture.bd=lecture.bd_Non 11.059908 100.00000 97.65 4.347616e-03
cinema=cinema_Non 12.265758 66.66667 58.70 1.129267e-02
cinema=cinema_Oui 8.716707 33.33333 41.30 1.129267e-02
lecture.bd=lecture.bd_Oui 0.000000 0.00000 2.35 4.347616e-03
bricol=bricol_Non 8.020924 42.59259 57.35 4.149911e-06
peche.chasse=peche.chasse_Non 0.000000 0.00000 88.80 2.257673e-282
v.test
peche.chasse=peche.chasse_Oui 35.908415
bricol=bricol_Oui 4.603730
lecture.bd=lecture.bd_Non 2.851773
cinema=cinema_Non 2.533509
cinema=cinema_Oui -2.533509
lecture.bd=lecture.bd_Oui -2.851773
bricol=bricol_Non -4.603730
peche.chasse=peche.chasse_Non -35.908415
$`3`
Cla/Mod Mod/Cla Global p.value v.test
cinema=cinema_Oui 86.31961 100.00000 41.30 0.000000e+00 Inf
peche.chasse=peche.chasse_Non 40.14640 100.00000 88.80 6.154083e-47 14.388011
sport=sport_Oui 52.97372 53.71669 36.15 1.222033e-33 12.088015
lecture.bd=lecture.bd_Non 36.50794 100.00000 97.65 7.397824e-10 6.157337
bricol=bricol_Oui 40.21102 48.10659 42.65 2.493205e-04 3.662957
cuisine=cuisine_Oui 39.38706 48.66760 44.05 2.003812e-03 3.089667
hard.rock=hard.rock_Non 35.90131 100.00000 99.30 2.035491e-03 3.085005
hard.rock=hard.rock_Oui 0.00000 0.00000 0.70 2.035491e-03 -3.085005
cuisine=cuisine_Non 32.70777 51.33240 55.95 2.003812e-03 -3.089667
bricol=bricol_Non 32.25806 51.89341 57.35 2.493205e-04 -3.662957
lecture.bd=lecture.bd_Oui 0.00000 0.00000 2.35 7.397824e-10 -6.157337
sport=sport_Non 25.84182 46.28331 63.85 1.222033e-33 -12.088015
peche.chasse=peche.chasse_Oui 0.00000 0.00000 11.20 6.154083e-47 -14.388011
cinema=cinema_Non 0.00000 0.00000 58.70 0.000000e+00 -Inf
$`4`
Cla/Mod Mod/Cla Global p.value v.test
lecture.bd=lecture.bd_Oui 100.000000 100.00000 2.35 3.168360e-96 20.814956
cinema=cinema_Oui 3.510896 61.70213 41.30 4.803168e-03 2.819946
sport=sport_Oui 3.319502 51.06383 36.15 3.601926e-02 2.096710
sport=sport_Non 1.801096 48.93617 63.85 3.601926e-02 -2.096710
cinema=cinema_Non 1.533220 38.29787 58.70 4.803168e-03 -2.819946
lecture.bd=lecture.bd_Non 0.000000 0.00000 97.65 3.168360e-96 -20.814956
$`5`
Cla/Mod Mod/Cla Global p.value v.test
hard.rock=hard.rock_Oui 100.0000000 100.00000 0.7 5.569208e-36 12.523271
cinema=cinema_Oui 1.4527845 85.71429 41.3 9.122223e-04 3.316287
cinema=cinema_Non 0.1703578 14.28571 58.7 9.122223e-04 -3.316287
hard.rock=hard.rock_Non 0.0000000 0.00000 99.3 5.569208e-36 -12.523271Une représentation graphique indiquant les modalités contribuant le plus à chaque axe est même directement disponible. La couleur bleue indique que la modalité est sous-représentée dans la classe et la couleur rouge qu’elle est sur-représentée11.
11 Attention à l’interprétation : ce code couleur est l’inverse de celui utilisé par GGally::ggtable().
40.6 webin-R
La CAH est présentée sur YouTube dans le webin-R #12 (Classification Ascendante Hiérarchique).