library(tidyverse)
library(labelled)
data(hdv2003, package = "questionr")
d <-
hdv2003 |>
mutate(
sexe = sexe |> fct_relevel("Femme"),
groupe_ages = age |>
cut(
c(18, 25, 45, 65, 99),
right = FALSE,
include.lowest = TRUE,
labels = c("18-24 ans", "25-44 ans",
"45-64 ans", "65 ans et plus")
),
etudes = nivetud |>
fct_recode(
"Primaire" = "N'a jamais fait d'etudes",
"Primaire" = "A arrete ses etudes, avant la derniere annee d'etudes primaires",
"Primaire" = "Derniere annee d'etudes primaires",
"Secondaire" = "1er cycle",
"Secondaire" = "2eme cycle",
"Technique / Professionnel" = "Enseignement technique ou professionnel court",
"Technique / Professionnel" = "Enseignement technique ou professionnel long",
"Supérieur" = "Enseignement superieur y compris technique superieur"
) |>
fct_na_value_to_level("Non documenté")
) |>
set_variable_labels(
sport = "Pratique un sport ?",
sexe = "Sexe",
groupe_ages = "Groupe d'âges",
etudes = "Niveau d'études",
heures.tv = "Heures de télévision / jour"
)26 Interactions
Dans un modèle statistique classique, on fait l’hypothèse implicite que chaque variable explicative est indépendante des autres. Cependant, cela ne se vérifie pas toujours. Par exemple, l’effet de l’âge peut varier en fonction du sexe.
Nous pourrons dès lors ajouter à notre modèle des interactions entre variables.
26.1 Données d’illustration
Reprenons le modèle que nous avons utilisé dans le chapitre sur la régression logistique binaire (cf. Chapitre 22).
26.2 Modèle sans interaction
Nous avions alors exploré les facteurs associés au fait de pratiquer du sport.
| Caractéristique | OR1 | 95% IC1 | p-valeur |
|---|---|---|---|
| Sexe | |||
| Femme | — | — | |
| Homme | 1,52 | 1,24 – 1,87 | <0,001 |
| Groupe d'âges | |||
| 18-24 ans | — | — | |
| 25-44 ans | 0,68 | 0,43 – 1,06 | 0,084 |
| 45-64 ans | 0,36 | 0,23 – 0,57 | <0,001 |
| 65 ans et plus | 0,27 | 0,16 – 0,46 | <0,001 |
| Niveau d'études | |||
| Primaire | — | — | |
| Secondaire | 2,54 | 1,73 – 3,75 | <0,001 |
| Technique / Professionnel | 2,81 | 1,95 – 4,10 | <0,001 |
| Supérieur | 6,55 | 4,50 – 9,66 | <0,001 |
| Non documenté | 8,54 | 4,51 – 16,5 | <0,001 |
| Heures de télévision / jour | 0,89 | 0,83 – 0,95 | <0,001 |
| 1 OR = rapport de cotes, IC = intervalle de confiance | |||
Selon les résultats de notre modèle, les hommes pratiquent plus un sport que les femmes et la pratique du sport diminue avec l’âge.
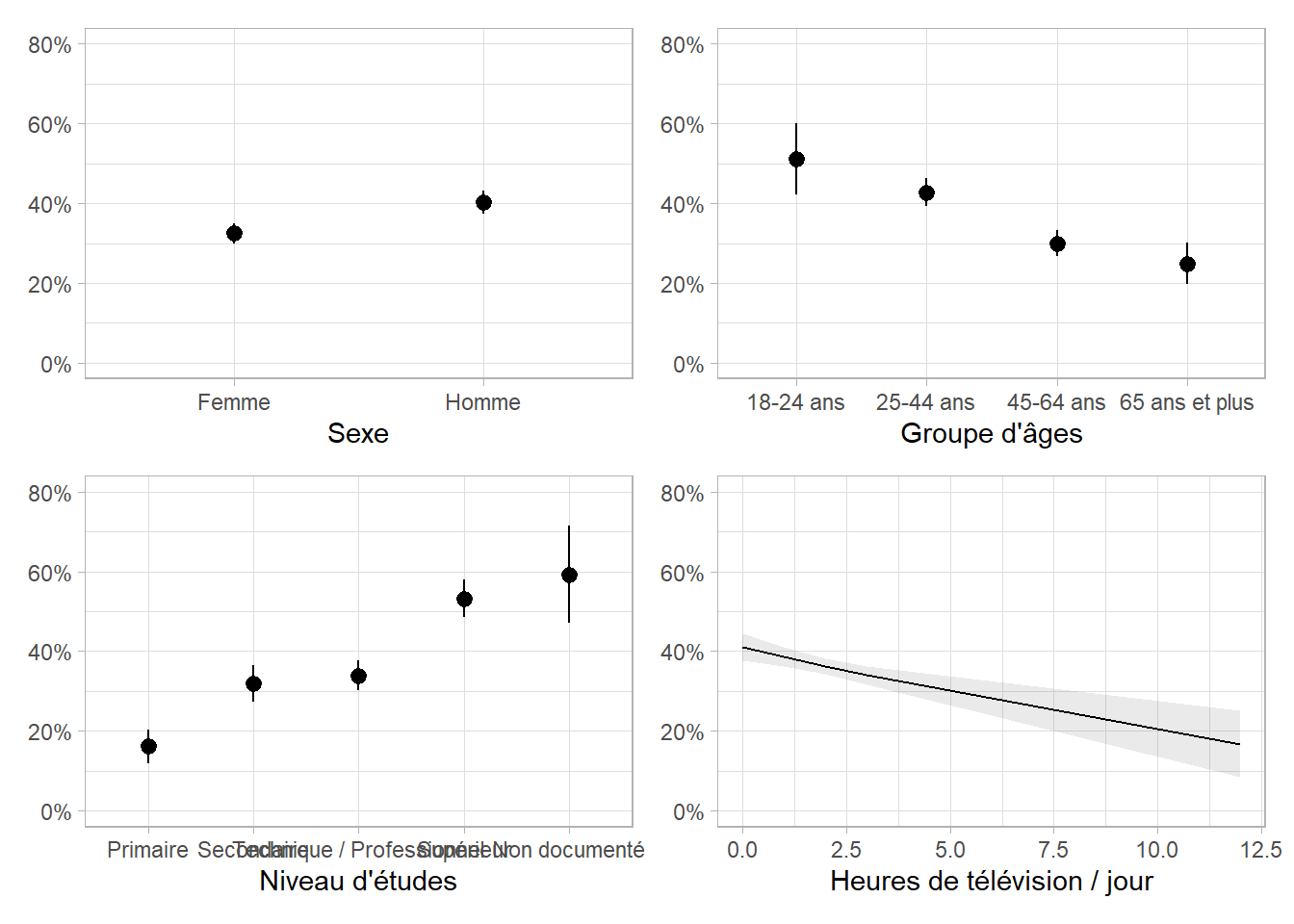
Dans le chapitre sur les estimations marginales, cf. Chapitre 24, nous avons présenté la fonction broom.helpers::plot_marginal_predictions() qui permet de représenter les prédictions marginales moyennes du modèle.
26.3 Définition d’une interaction
Cependant, l’effet de l’âge est-il le même selon le sexe ? Nous allons donc introduire une interaction entre l’âge et le sexe dans notre modèle, ce qui sera représenté par sexe * groupe_agesdans l’équation du modèle.
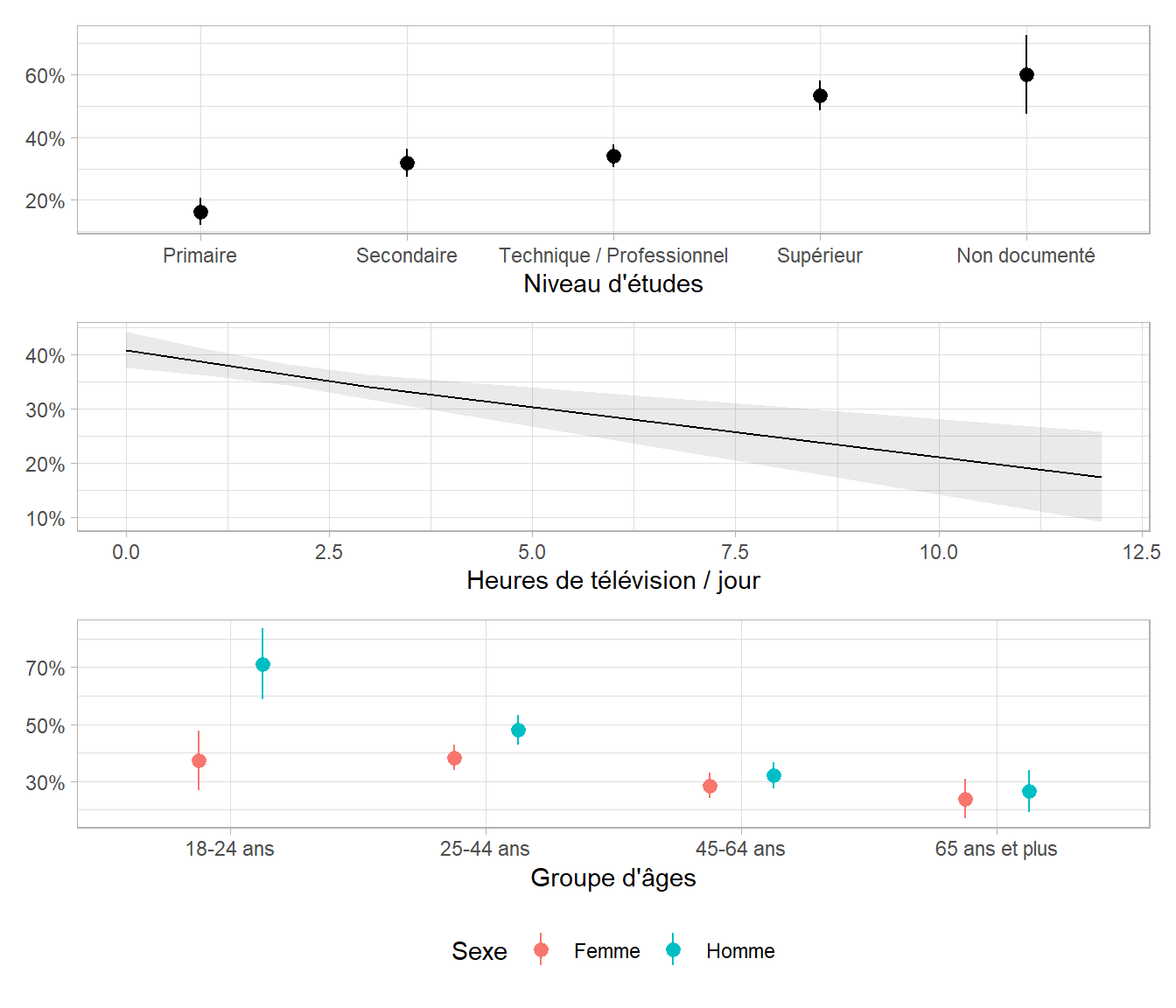
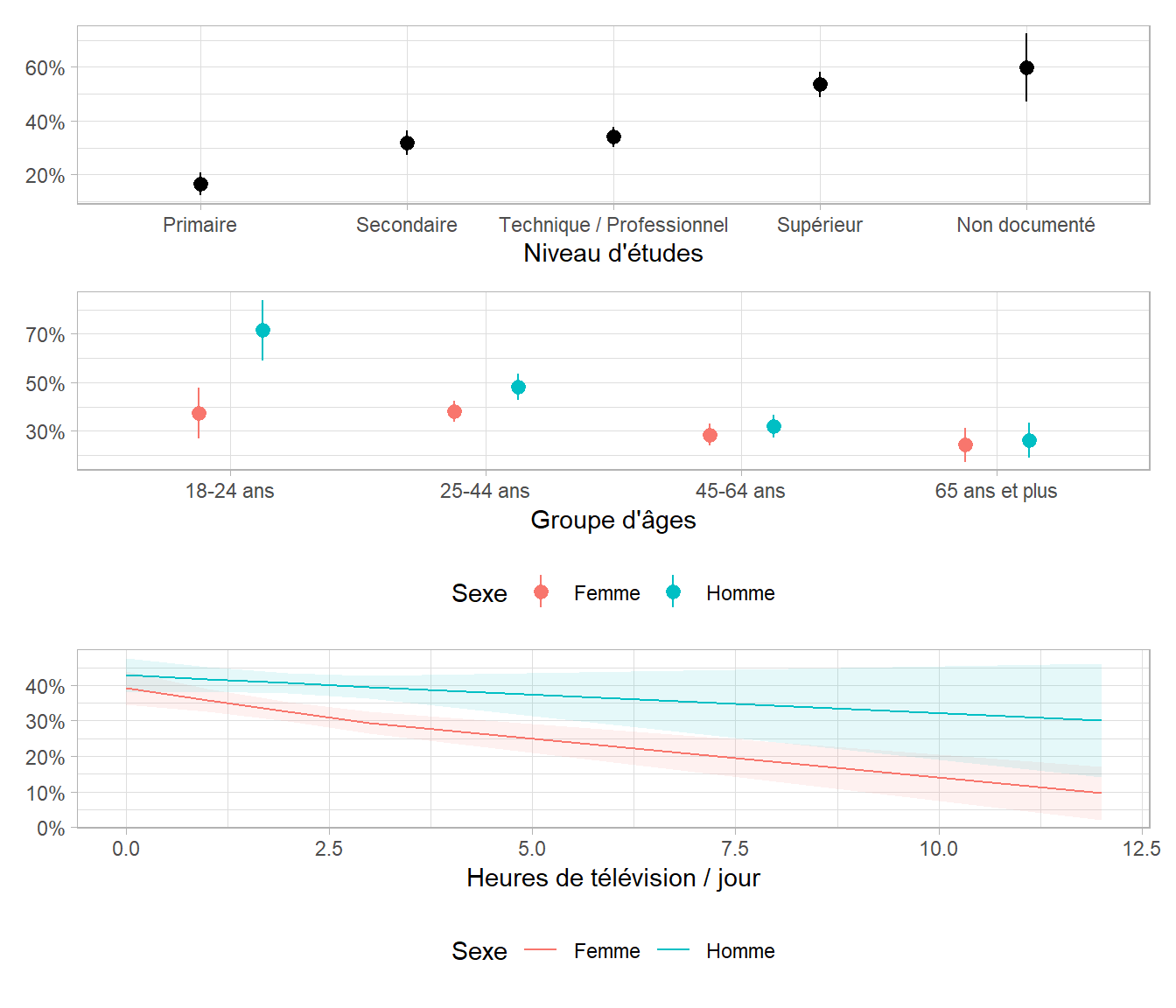
Commençons par regarder les prédictions marginales du modèle avec interaction.
mod2 |>
broom.helpers::plot_marginal_predictions(type = "response") |>
patchwork::wrap_plots(ncol = 1) &
scale_y_continuous(
labels = scales::label_percent()
)
Sur ce graphique, on voit que la pratique d’un sport diminue fortement avec l’âge chez les hommes, tandis que cette diminution est bien plus modérée chez les femmes.
Astuce
Par défaut, broom.helpers::plot_marginal_predictions() détecte la présence d’interactions dans le modèle et calcule les prédictions marginales pour chaque combinaison de variables incluent dans une interaction. Il reste possible de calculer des prédictions marginales individuellement pour chaque variable du modèle. Pour cela, il suffit d’indiquer variables_list = "no_interaction".
26.4 Significativité de l’interaction
L’ajout d’une interaction au modèle augmente la capacité prédictive du modèle mais, dans le même temps, augmente le nombre de coefficients (et donc de degrés de liberté). La question se pose donc de savoir si l’ajout d’un terme d’interaction améliore notre modèle.
En premier lieu, nous pouvons comparer les AIC des modèles avec et sans interaction.
L’AIC du modèle avec interaction est plus faible que celui sans interaction, nous indiquant un gain : notre modèle avec interaction est donc meilleur.
On peut tester avec car::Anova() si l’interaction est statistiquement significative1.
1 Lorsqu’il y a une interaction, il est préférable d’utiliser le type III, cf. Section 22.8. En toute rigueur, il serait préférable de coder nos variables catégorielles avec un contraste de type somme (cf. Chapitre 25). En pratique, nous pouvons nous en passer ici.
Analysis of Deviance Table (Type III tests)
Response: sport
LR Chisq Df Pr(>Chisq)
sexe 19.349 1 1.089e-05 ***
groupe_ages 15.125 3 0.0017131 **
etudes 125.575 4 < 2.2e-16 ***
heures.tv 12.847 1 0.0003381 ***
sexe:groupe_ages 13.023 3 0.0045881 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La p-valeur associée au terme d’interaction (sexe:groupe_ages) est inférieure à 1% : l’interaction a donc bien un effet significatif.
Nous pouvons également utiliser gtsummary::add_global_p().
| Caractéristique | OR1 | 95% IC1 | p-valeur |
|---|---|---|---|
| Sexe | <0,001 | ||
| Femme | — | — | |
| Homme | 5,10 | 2,41 – 11,4 | |
| Groupe d'âges | 0,002 | ||
| 18-24 ans | — | — | |
| 25-44 ans | 1,06 | 0,61 – 1,85 | |
| 45-64 ans | 0,64 | 0,36 – 1,15 | |
| 65 ans et plus | 0,49 | 0,25 – 0,97 | |
| Niveau d'études | <0,001 | ||
| Primaire | — | — | |
| Secondaire | 2,55 | 1,74 – 3,78 | |
| Technique / Professionnel | 2,84 | 1,97 – 4,14 | |
| Supérieur | 6,69 | 4,60 – 9,89 | |
| Non documenté | 8,94 | 4,64 – 17,6 | |
| Heures de télévision / jour | 0,89 | 0,83 – 0,95 | <0,001 |
| Sexe * Groupe d'âges | 0,005 | ||
| Homme * 25-44 ans | 0,31 | 0,13 – 0,70 | |
| Homme * 45-64 ans | 0,24 | 0,10 – 0,54 | |
| Homme * 65 ans et plus | 0,23 | 0,09 – 0,60 | |
| 1 OR = rapport de cotes, IC = intervalle de confiance | |||
26.5 Interprétation des coefficients
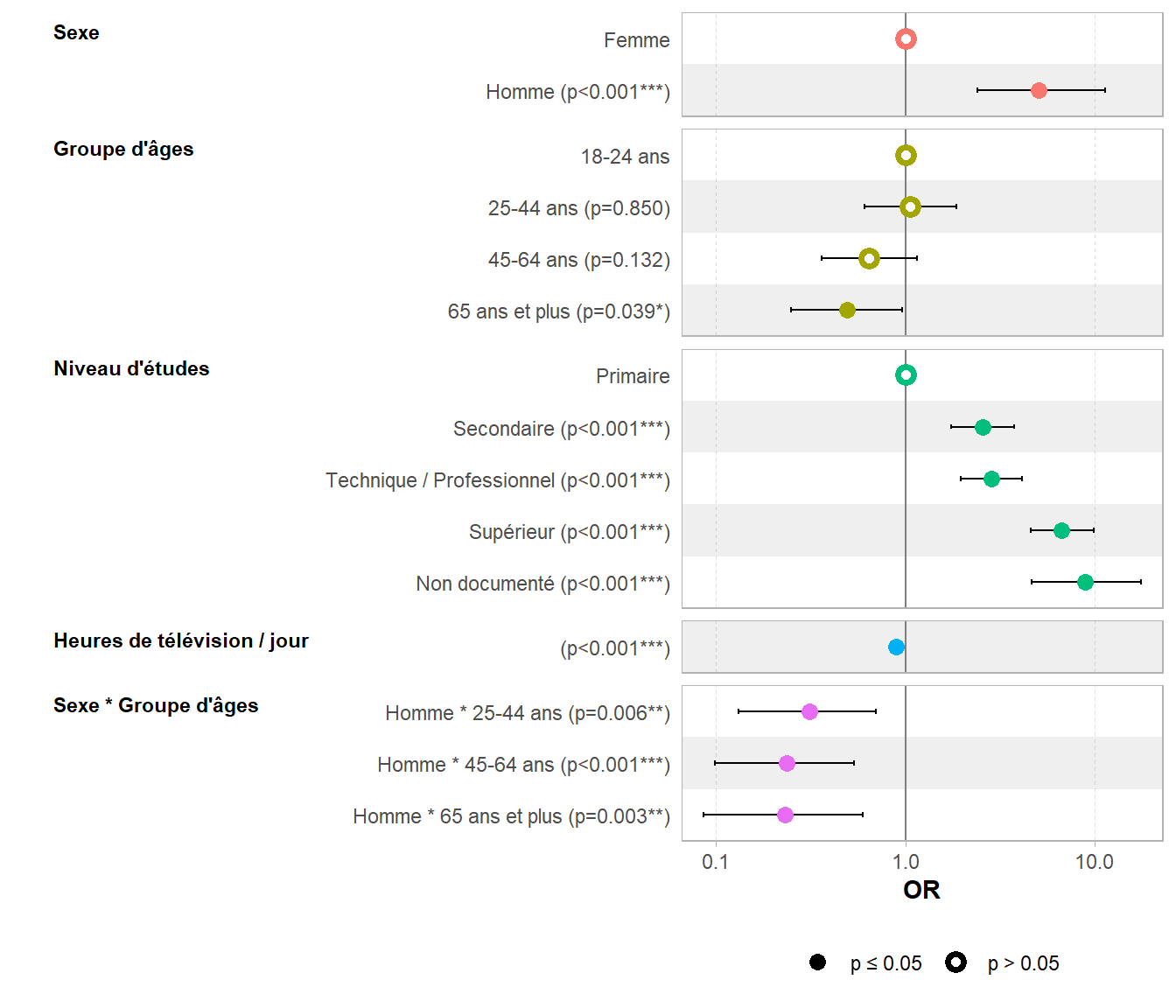
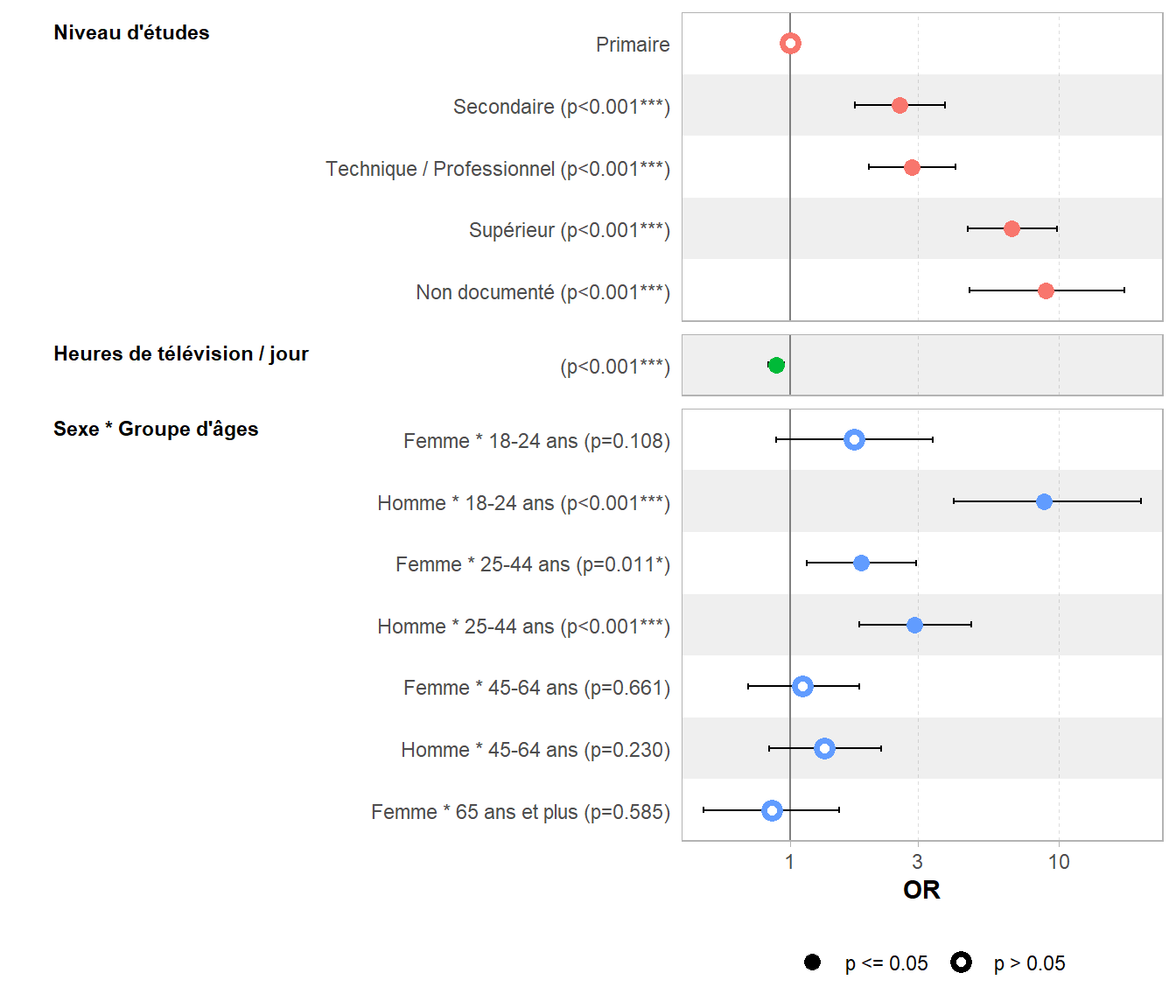
Jetons maintenant un œil aux coefficients du modèle. Pour rendre les choses plus visuelles, nous aurons recours à ggtstats::ggcoef_model().
Concernant les variables sexe et groupe_ages, nous avons trois séries de coefficients : une série pour le sexe, une pour le groupe d’âges et enfin des coefficients pour l’interaction entre le sexe et le groupe d’âges.
Pour bien interpréter ces coefficients, il faut toujours avoir en tête les modalités choisies comme référence pour chaque variable.
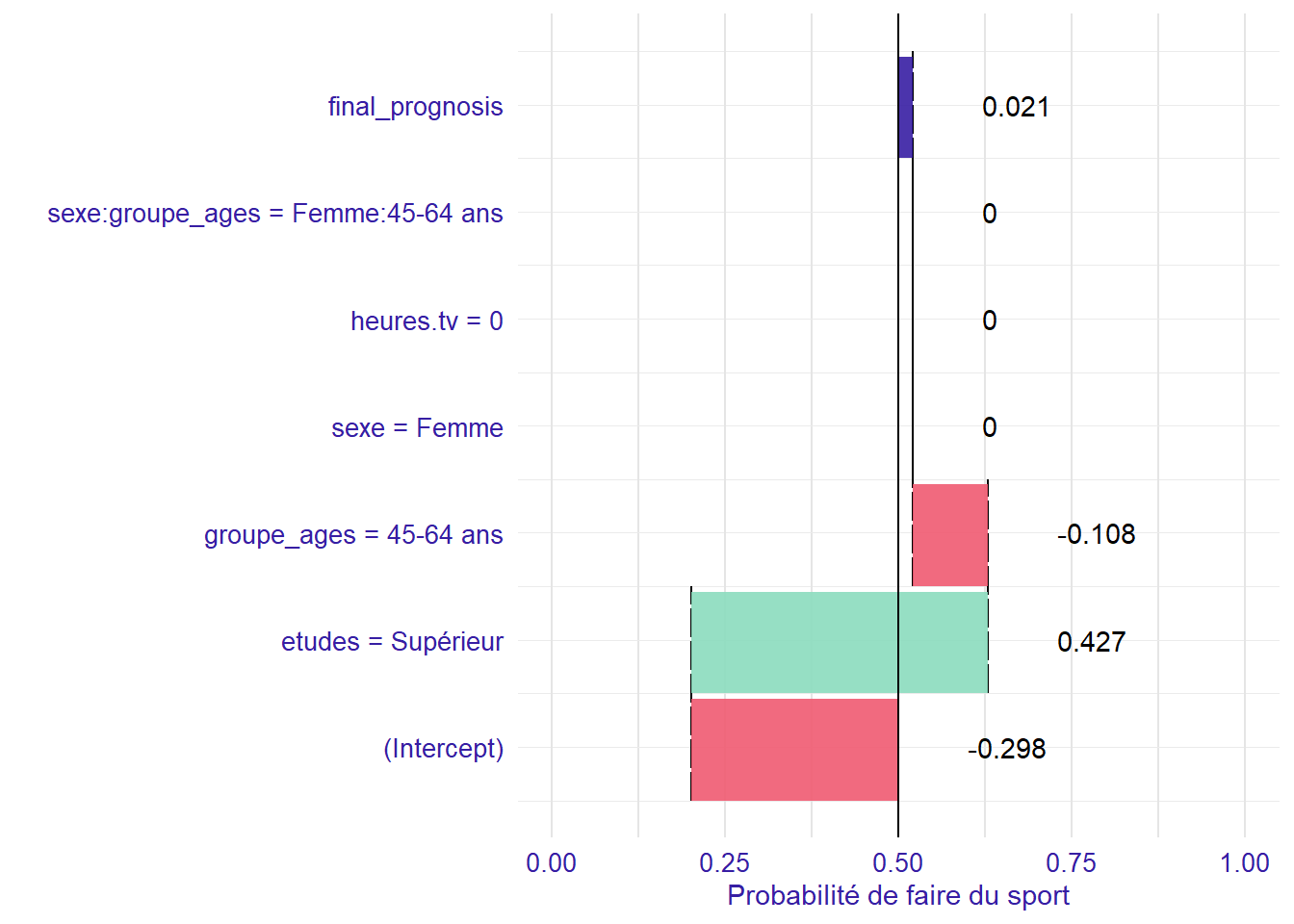
Supposons une femme de 60 ans, dont toutes les autres variables correspondent aux modalités de référence (i.e. de niveau primaire, qui ne regarde pas la télévision). Regardons ce que prédit le modèle quant à sa probabilité de faire du sport au travers d’une représentation graphique, grâce au package breakDown.
library(breakDown)
logit <- function(x) exp(x)/(1+exp(x))
nouvelle_observation <- d[1, ]
nouvelle_observation$sexe[1] = "Femme"
nouvelle_observation$groupe_ages[1] = "45-64 ans"
nouvelle_observation$etud[1] = "Primaire"
nouvelle_observation$heures.tv[1] = 0
plot(
broken(mod2, nouvelle_observation, predict.function = betas),
trans = logit
) +
ylim(0, 1) +
ylab("Probabilité de faire du sport")
En premier lieu, l’intercept s’applique et permet de déterminer la probabilité de base de faire du sport à la référence. Femme
étant la modalité de référence pour la variable sexe, cela ne modifie pas le calcul de la probabilité de faire du sport. Par contre, il y a une modification induite par la modalité 45-64 ans
de la variable groupe_ages.
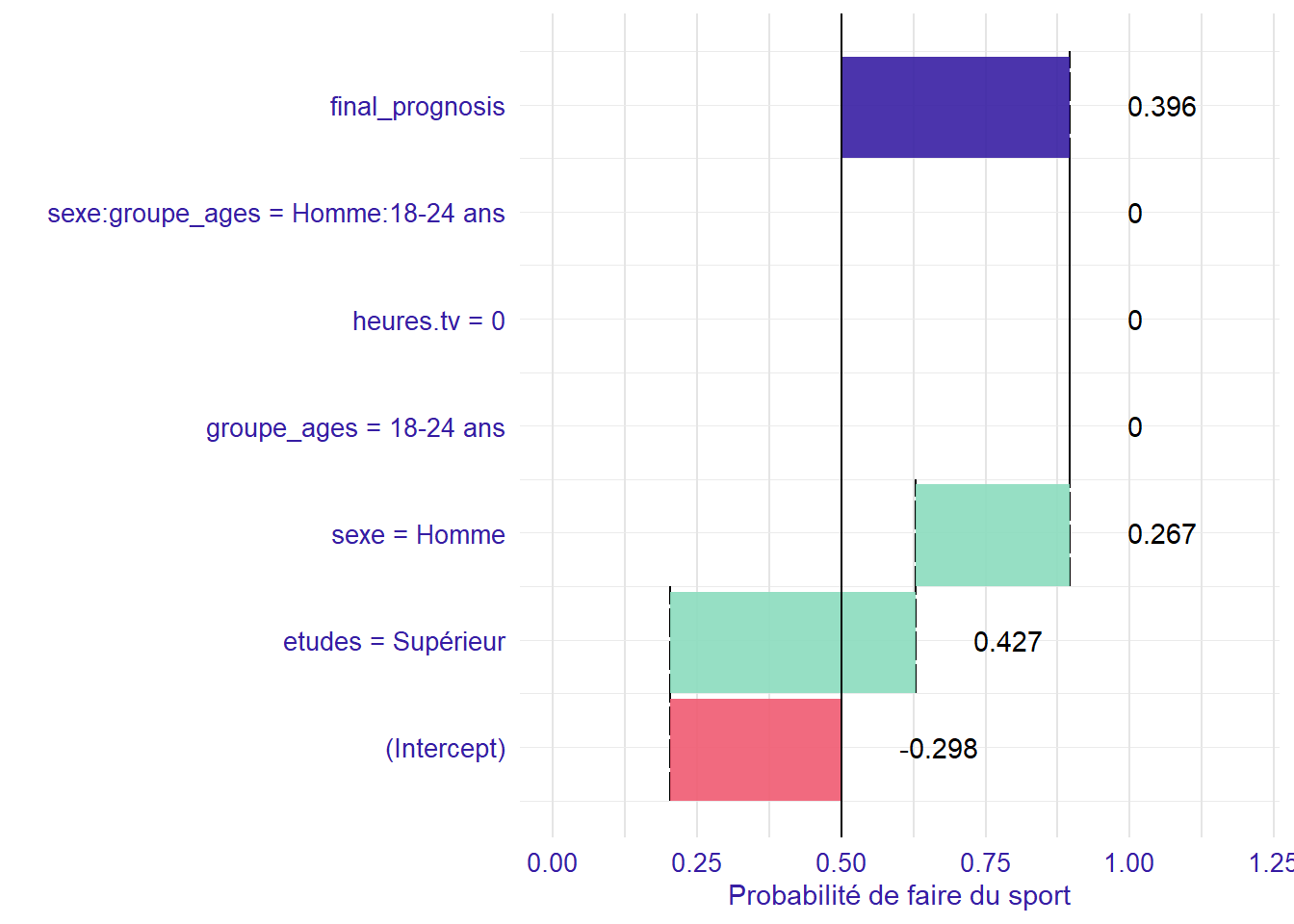
Regardons maintenant la situation d’un homme de 20 ans.
nouvelle_observation$sexe[1] = "Homme"
nouvelle_observation$groupe_ages[1] = "18-24 ans"
plot(
broken(mod2, nouvelle_observation, predict.function = betas),
trans = logit
) +
ylim(0, 1.2) +
ylab("Probabilité de faire du sport")
Nous sommes à la modalité de référence pour l’âge par contre il y a un effet important du sexe. Le coefficient associé globalement à la variable sexe correspond donc à l’effet du sexe à la modalité de référence du groupe d’âges.
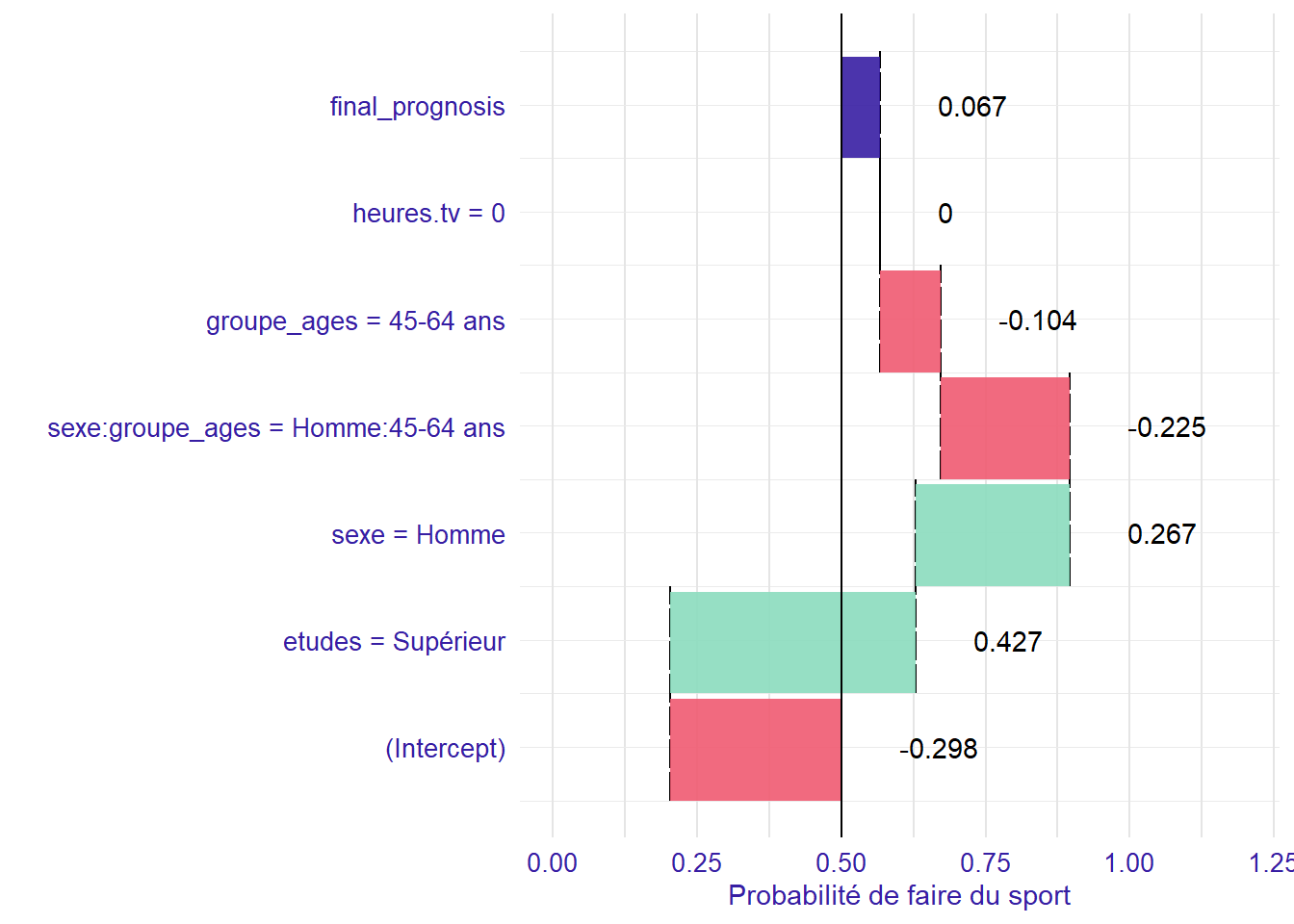
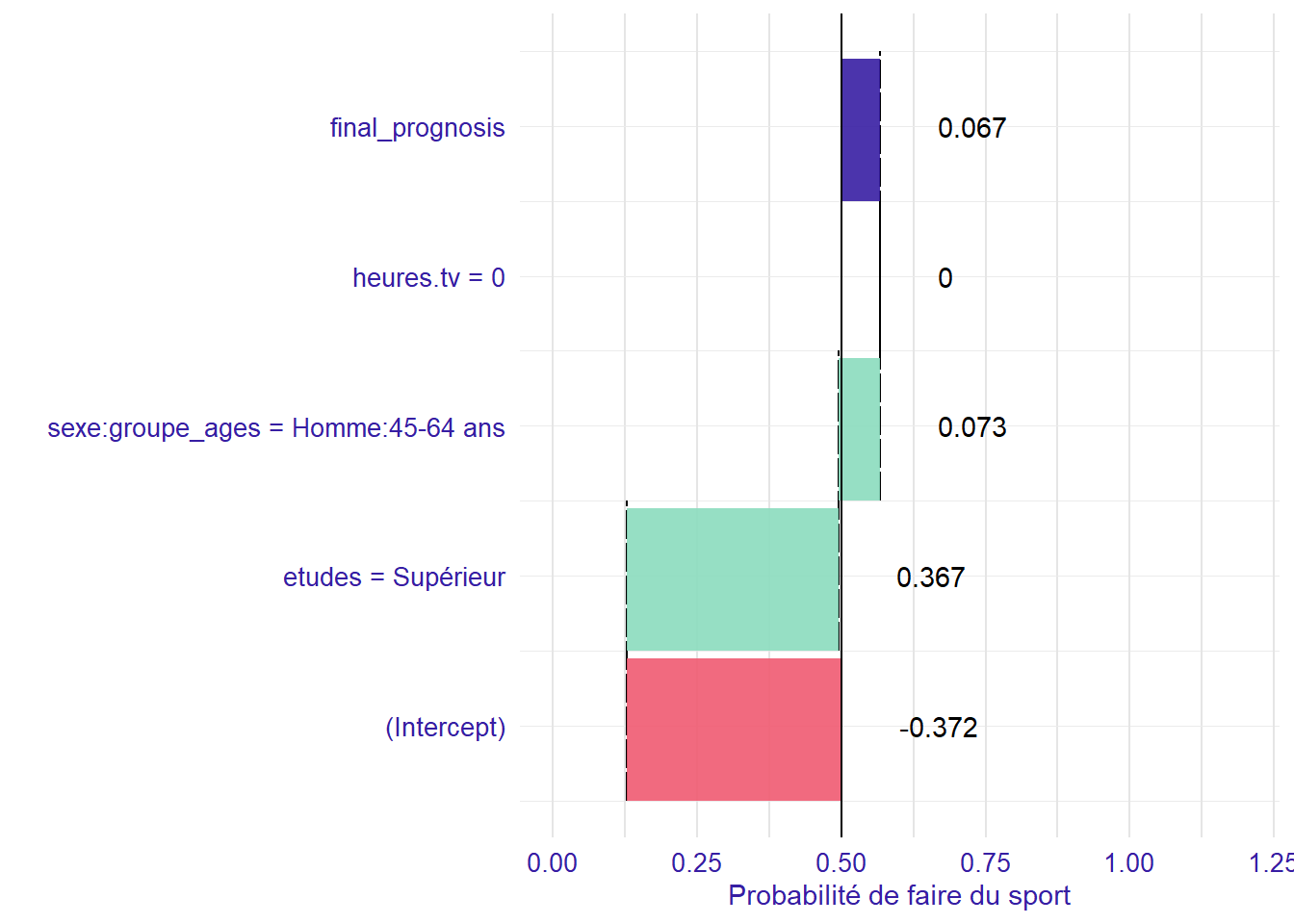
Regardons enfin la situation d’un homme de 60 ans.
nouvelle_observation$groupe_ages[1] = "45-64 ans"
plot(
broken(mod2, nouvelle_observation, predict.function = betas),
trans = logit
) +
ylim(0, 1.2) +
ylab("Probabilité de faire du sport")
Cette fois, plusieurs coefficients s’appliquent : à la fois le coefficient sexe = Homme
(effet du sexe pour les 18-24 ans), le coefficient groupe_ages = 45-64 ans
qui est l’effet de l’âge pour les femmes de 45-64 ans par rapport aux 18-24 ans et le coefficient sexe:groupe_ages = Homme:45-64 ans
qui indique l’effet spécifique qui s’applique aux hommes de 45-64 ans, d’une part par rapport aux femmes du même âge et d’autre part par rapport aux hommes de 18-24 ans. L’effet des coefficients d’interaction doivent donc être interprétés par rapport aux autres coefficients du modèle qui s’appliquent, en tenant compte des modalités de référence.
26.6 Définition alternative de l’interaction
Il est cependant possible d’écrire le même modèle différemment. En effet, sexe * groupe_ages dans la formule du modèle est équivalent à l’écriture sexe + groupe_ages + sexe:groupe_ages, c’est-à-dire que l’on demande des coefficients pour la variable sexe à la référence de groupe_ages, des coefficients pour groupe_ages à la référence de sexe et enfin des coefficients pour tenir compte de l’interaction.
On peut se contenter d’une série de coefficients uniques pour l’interaction en indiquant seulement sexe : groupe_ages.
Au sens strict, ce modèle explique tout autant le phénomène étudié que le modèle précédent. On peut le vérifier facilement avec stats::anova().
Analysis of Deviance Table
Model 1: sport ~ sexe * groupe_ages + etudes + heures.tv
Model 2: sport ~ sexe:groupe_ages + etudes + heures.tv
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 1982 2197.4
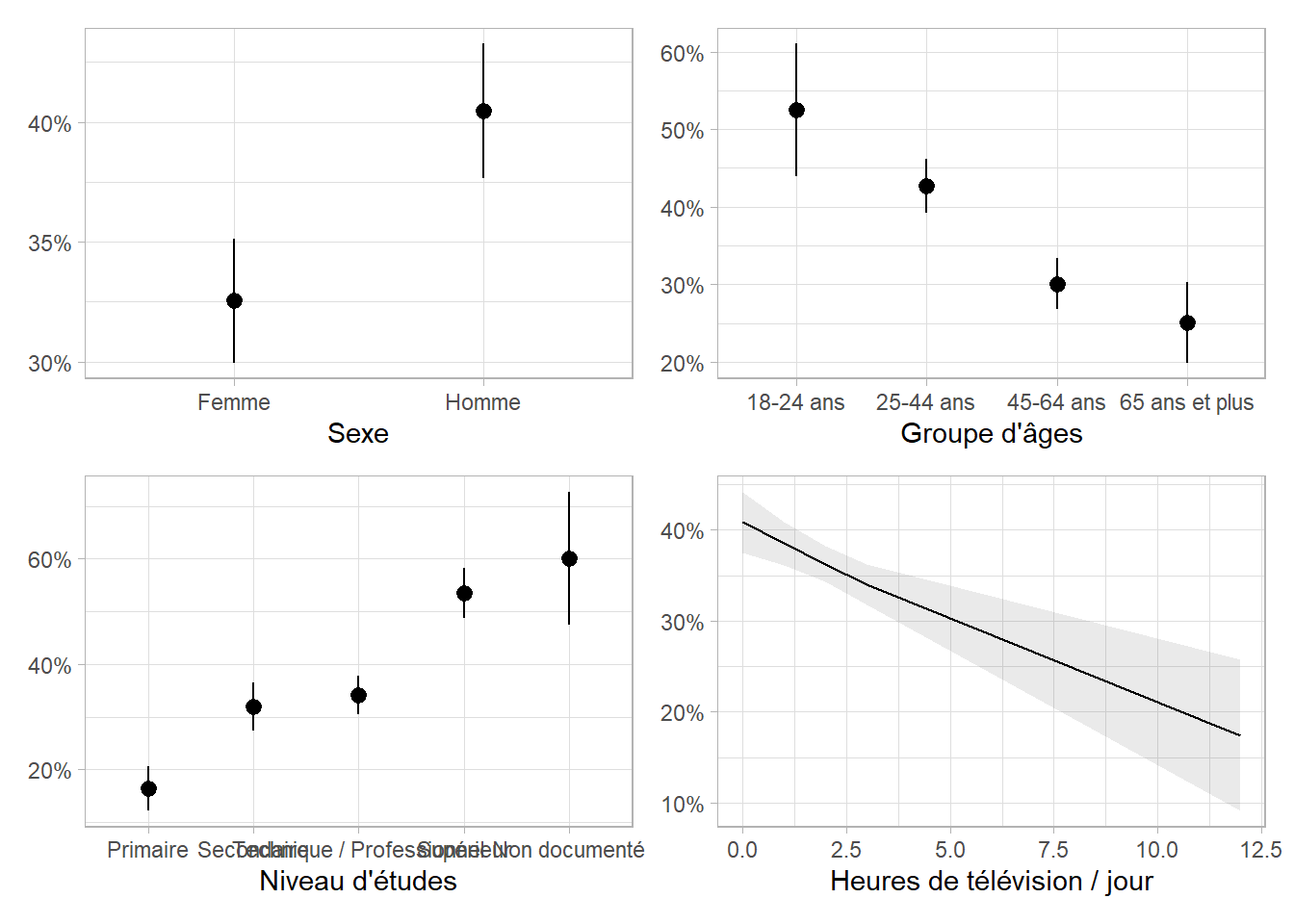
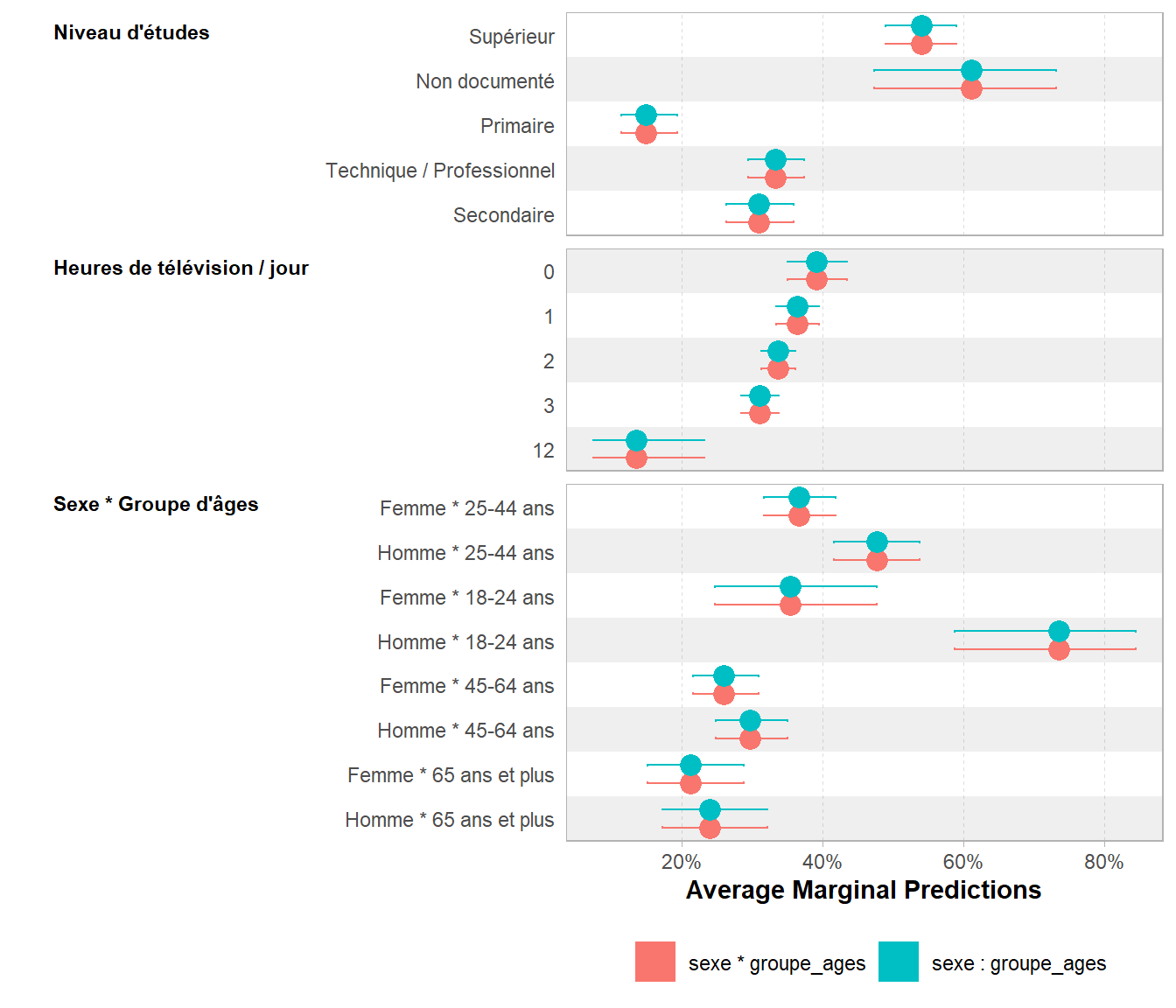
2 1982 2197.4 0 0 De même, les prédictions marginales sont les mêmes, comme nous pouvons le constater avec ggstats::ggcoef_compare().
ggstats::ggcoef_compare(
list("sexe * groupe_ages" = mod2, "sexe : groupe_ages" = mod3),
tidy_fun = broom.helpers::tidy_marginal_predictions,
significance = NULL,
vline = FALSE
) +
scale_x_continuous(labels = scales::label_percent())Warning: Model matrix is rank deficient. Some variance-covariance parameters are
missing.
Warning: Model matrix is rank deficient. Some variance-covariance parameters are
missing.
Warning: Model matrix is rank deficient. Some variance-covariance parameters are
missing.
Par contre, regardons d’un peu plus près les coefficients de ce nouveau modèle. Nous allons voir que leur interprétation est légèrement différente.
Cette fois-ci, il n’y a plus de coefficients globaux pour la variable sexe ni pour groupe_ages mais des coefficients pour chaque combinaison de ces deux variables. Reprenons l’exemple de notre homme de 60 ans.
plot(
broken(mod3, nouvelle_observation, predict.function = betas),
trans = logit
) +
ylim(0, 1.2) +
ylab("Probabilité de faire du sport")
Cette fois-ci, le coefficient d’interaction fournit indique l’effet combiné du sexe et du groupe d’âges par rapport à la situation de référence (femme de 18-24 ans).
Que l’on définisse une interaction simple (sexe:groupe_ages) ou complète (sexe*groupe_ages), les deux modèles calculés sont donc identiques en termes prédictifs et explicatifs, mais l’interprétation de leurs coefficients diffèrent.
26.7 Identifier les interactions pertinentes
Il peut y avoir de multiples interactions dans un modèle, d’ordre 2 (entre deux variables) ou plus (entre trois variables ou plus). Il est toujours bon, selon notre connaissance du sujet et de la littérature, d’explorer manuellement les interactions attendues / prévisibles.
Mais, il est tentant de vouloir tester les multiples interactions possibles de manière itératives afin d’identifier celles à retenir.
Une possibilité2 est d’avoir recours à une sélection de modèle pas à pas ascendante (voir Chapitre 23). Nous allons partir de notre modèle sans interaction, indiquer à step() l’ensemble des interactions possibles et voir si nous pouvons minimiser l’AIC.
2 On pourra également regarder du côté de glmulti::glmulti() pour des approches alternatives.
Start: AIC=2230.4
sport ~ sexe + groupe_ages + etudes + heures.tv
Df Deviance AIC
+ sexe:groupe_ages 3 2197.4 2223.4
+ sexe:etudes 4 2199.6 2227.6
+ sexe:heures.tv 1 2207.6 2229.6
<none> 2210.4 2230.4
+ groupe_ages:heures.tv 3 2207.0 2233.0
+ etudes:heures.tv 4 2207.4 2235.4
+ groupe_ages:etudes 11 2194.6 2236.6
- heures.tv 1 2224.0 2242.0
- sexe 1 2226.4 2244.4
- groupe_ages 3 2260.6 2274.6
- etudes 4 2334.3 2346.3
Step: AIC=2223.38
sport ~ sexe + groupe_ages + etudes + heures.tv + sexe:groupe_ages
Df Deviance AIC
+ sexe:heures.tv 1 2194.7 2222.7
<none> 2197.4 2223.4
+ groupe_ages:heures.tv 3 2193.5 2225.5
+ sexe:etudes 4 2192.1 2226.1
+ etudes:heures.tv 4 2194.6 2228.6
- sexe:groupe_ages 3 2210.4 2230.4
+ groupe_ages:etudes 11 2183.1 2231.1
- heures.tv 1 2210.2 2234.2
- etudes 4 2323.0 2341.0
Step: AIC=2222.67
sport ~ sexe + groupe_ages + etudes + heures.tv + sexe:groupe_ages +
sexe:heures.tv
Df Deviance AIC
<none> 2194.7 2222.7
- sexe:heures.tv 1 2197.4 2223.4
+ groupe_ages:heures.tv 3 2190.4 2224.4
+ sexe:etudes 4 2189.0 2225.0
+ etudes:heures.tv 4 2191.6 2227.6
- sexe:groupe_ages 3 2207.6 2229.6
+ groupe_ages:etudes 11 2180.7 2230.7
- etudes 4 2319.9 2339.9sport ~ sexe + groupe_ages + etudes + heures.tv + sexe:groupe_ages +
sexe:heures.tvLe modèle final suggéré comprends une interaction entre le sexe et le groupe d’âges et une interaction entre le sexe et le nombre quotidien d’heures de télévision. Nous pouvons utiliser broom.helpers::plot_marginal_predictions() pour visualiser l’effet de ces deux interactions.
26.8 Pour aller plus loin
Il y a d’autres extensions dédiées à l’analyse des interactions d’un modèle, de même que de nombreux supports de cours en ligne dédiés à cette question.
- Les effets d’interaction par Jean-François Bickel
- Analysing interactions of fitted models par Helios De Rosario Martínez
26.9 webin-R
Les interactions sont abordées dans le webin-R #07 (régression logistique partie 2) sur YouTube.