42 Régression logistique ordinale
La régression logistique ordinale est une extension de la régression logistique binaire (cf. Chapitre 22) aux variables qualitatives à trois modalités ou plus qui sont ordonnées, par exemple modéré, moyen et fort.
Pour une variable ordonnée, il est possible de réaliser une régression logistique multinomiale (cf. Chapitre 41) comme on le ferait avec une variable non ordonnée. Dans ce cas de figure, chaque modalité de la variable d’intérêt serait comparée à une modalité de référence.
Alternativement, on peut réaliser une régression logistique ordinale aussi appelée modèle cumulatif ou modèle logistique à égalité des pentes. Ce type de modèle est plus simple que la régression multinomiale car il ne renvoie qu’un seul jeu de coefficients.
Supposons une variable d’intérêt à trois modalités A, B et C telles que A < B < C. Les odds ratios qui seront calculés comparerons la probabilité que Y≥B par rapport à la probabilité que Y≤A (aspect cumulatif) et ferons l’hypothèse que ce ratio est le même quand on compare la probabilité que Y≥C par rapport à la probabilité que Y≤B (égalité des pentes).
42.1 Données d’illustration
Pour illustrer la régression logistique multinomiale, nous allons reprendre le jeu de données hdv2003 du package questionr et portant sur l’enquête histoires de vie 2003 de l’Insee et l’exemple utilisé dans le chapitre sur la régression logistique multinomiale (cf. Chapitre 41).
Nous allons considérer comme variable d’intérêt la variable trav.satisf, à savoir la satisfaction ou l’insatisfaction au travail.
n % val%
Satisfaction 480 24.0 45.8
Insatisfaction 117 5.9 11.2
Equilibre 451 22.6 43.0
NA 952 47.6 NANous allons devoir ordonner les modalités de la plus faible à la plus forte.
Et nous allons indiquer qu’il s’agit d’un facteur ordonné.
Nous allons aussi en profiter pour raccourcir les étiquettes de la variable trav.imp :
Enfin, procédons à quelques recodages additionnels :
d <- d |>
mutate(
sexe = sexe |> fct_relevel("Femme"),
groupe_ages = age |>
cut(
c(18, 25, 45, 99),
right = FALSE,
include.lowest = TRUE,
labels = c("18-24 ans", "25-44 ans",
"45 et plus")
),
etudes = nivetud |>
fct_recode(
"Primaire" = "N'a jamais fait d'etudes",
"Primaire" = "A arrete ses etudes, avant la derniere annee d'etudes primaires",
"Primaire" = "Derniere annee d'etudes primaires",
"Secondaire" = "1er cycle",
"Secondaire" = "2eme cycle",
"Technique / Professionnel" = "Enseignement technique ou professionnel court",
"Technique / Professionnel" = "Enseignement technique ou professionnel long",
"Supérieur" = "Enseignement superieur y compris technique superieur"
) |>
fct_na_value_to_level("Non documenté")
) |>
set_variable_labels(
trav.satisf = "Satisfaction dans le travail",
sexe = "Sexe",
groupe_ages = "Groupe d'âges",
etudes = "Niveau d'études",
trav.imp = "Importance accordée au travail"
)42.2 Calcul du modèle ordinal
42.2.1 avec MASS::polr()
Le plus facile pour le calcul d’un modèle ordinal est d’avoir recours à la fonction MASS::polr().
Nous pouvons aisément simplifier le modèle avec step() (cf. Chapitre 23).
Start: AIC=1978.29
trav.satisf ~ sexe + etudes + groupe_ages + trav.imp
Df AIC
- groupe_ages 2 1977.2
- sexe 1 1978.3
<none> 1978.3
- etudes 4 1991.5
- trav.imp 3 2014.0
Step: AIC=1977.23
trav.satisf ~ sexe + etudes + trav.imp
Df AIC
- sexe 1 1977.0
<none> 1977.2
- etudes 4 1990.6
- trav.imp 3 2013.2
Step: AIC=1976.97
trav.satisf ~ etudes + trav.imp
Df AIC
<none> 1977.0
- etudes 4 1990.6
- trav.imp 3 2011.642.2.2 Fonctions alternatives
Un package alternatif pour le calcul de régressions ordinales est le package dédié ordinal et sa fonction ordinal::clm(). Pour les utilisateurs avancés, ordinal permet également de traiter certains prédicteurs comme ayant un effet nominal (et donc avec un coefficient par niveau) via l’argument nominal. Il existe également une fonction ordinal::clmm() permet de définir des modèles mixtes avec variables à effet aléatoire.
Les modèles créés avec ordinal::clm() sont plutôt bien traités par des fonctions comme gtsummary::tbl_regression() ou ggstats::ggcoef_model().
Enfin, on peut également citer la fonction VGAM::vgam() en spécifiant family = VGAM::cumulative(parallel = TRUE). Cette famille de modèles offre des options avancées (par exemple il est possible de calculer des modèles non parallèles, c’est-à-dire avec une série de coefficients pour chaque changement de niveau). Par contre, le support de gtsummary::tbl_regression() et ggstats::ggcoef_model() sera limité (seulement des résultats bruts).
En toute rigueur, il faudrait tester l’égalité des pentes. Laurent Rouvière propose un code permettant d’effectuer ce test sous R à partir d’un modèle réalisé avec VGAM::vglm(), voir la diapositive 33 sur 35 d’un de ses cours de janvier 2015 intitulé Quelques modèles logistiques polytomiques.
42.3 Affichage des résultats du modèle
Pour un tableau des coefficients, on peut tout simplement appeler gtsummary::tbl_regression(). Nous allons indiquer exponentiate = TRUE car, comme pour la régression logistique binaire, l’exponentielle des coefficients peut s’interpréter comme des odds ratios. Pour éviter certains messages d’information, nous allons préciser tidy_fun = broom.helpers::tidy_parameters (cela implique juste que le tableau des coefficients sera calculé avec le package parameters plutôt qu’avec le package broom). Nous pouvons calculer à la volée la p-valeur globale de chaque variable avec gtsummary::add_global_p().
rego2 |>
tbl_regression(
exponentiate = TRUE,
tidy_fun = broom.helpers::tidy_parameters
) |>
bold_labels() |>
add_global_p(keep = TRUE)
Réajustement pour obtenir le Hessien| Caractéristique | OR1 | 95% IC1 | p-valeur |
|---|---|---|---|
| Niveau d'études | <0,001 | ||
| Primaire | — | — | |
| Secondaire | 1,06 | 0,67 – 1,67 | 0,8 |
| Technique / Professionnel | 1,01 | 0,67 – 1,53 | >0,9 |
| Supérieur | 1,84 | 1,20 – 2,83 | 0,006 |
| Non documenté | 0,66 | 0,25 – 1,72 | 0,4 |
| Importance accordée au travail | <0,001 | ||
| Le plus | — | — | |
| Aussi | 1,39 | 0,65 – 2,97 | 0,4 |
| Moins | 1,03 | 0,50 – 2,14 | >0,9 |
| Peu | 0,19 | 0,08 – 0,48 | <0,001 |
| 1 OR = rapport de cotes, IC = intervalle de confiance | |||
La même commande fonctionne avec un modèle créé avec ordinal::clm().
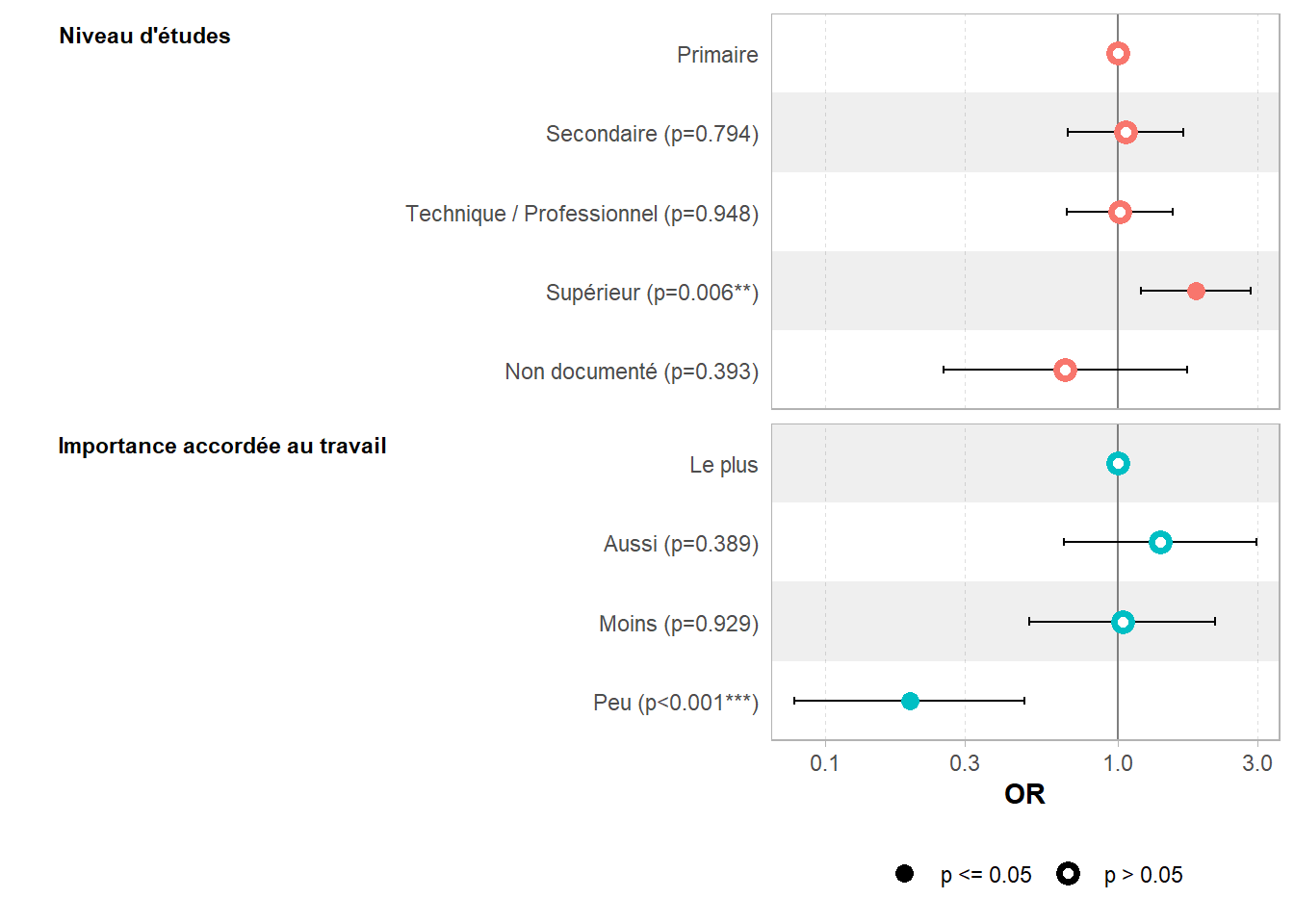
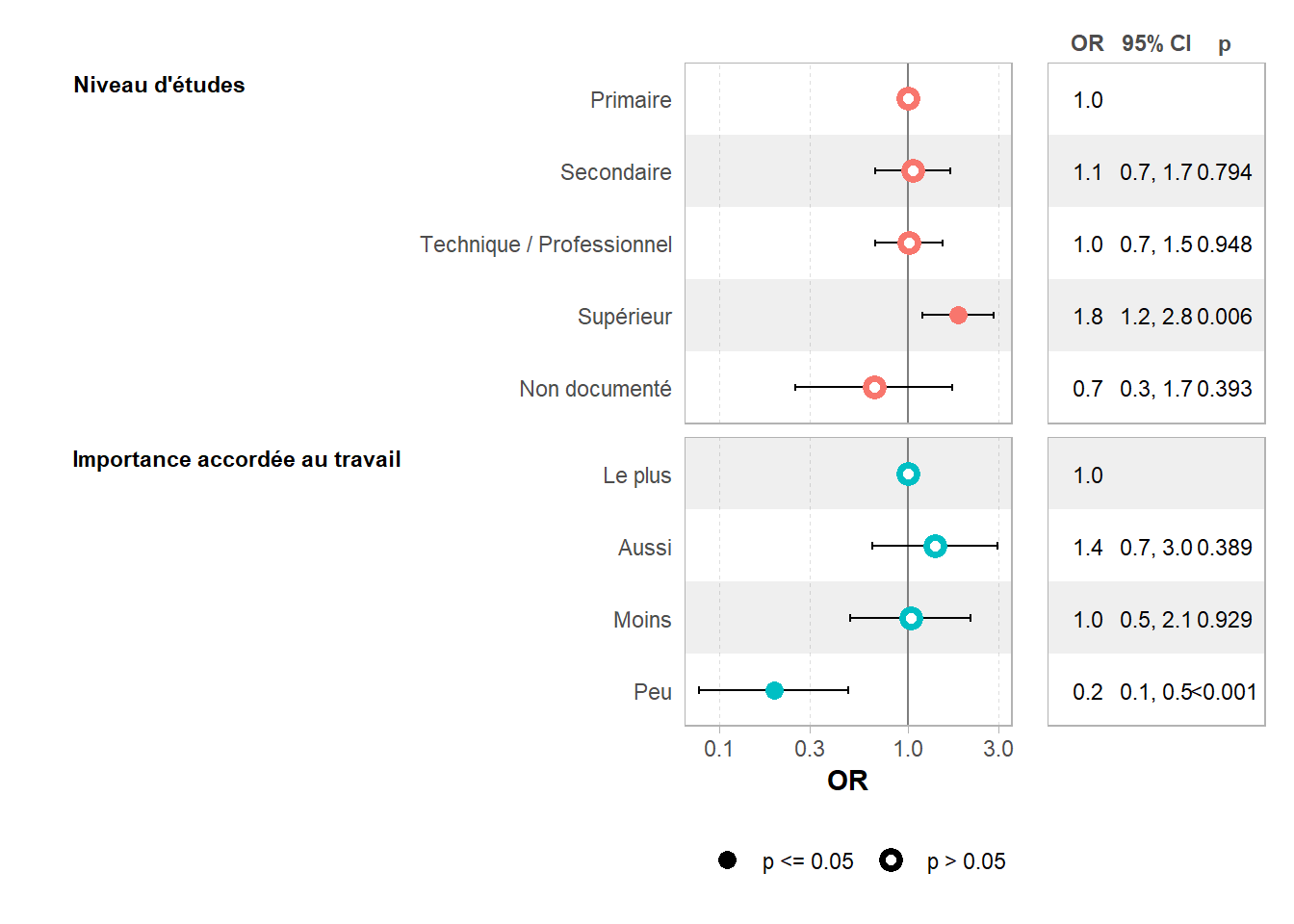
Pour un graphique des coefficients, on va procéder de même avec ggstats::gcoef_model() ou ggstats::gcoef_table().
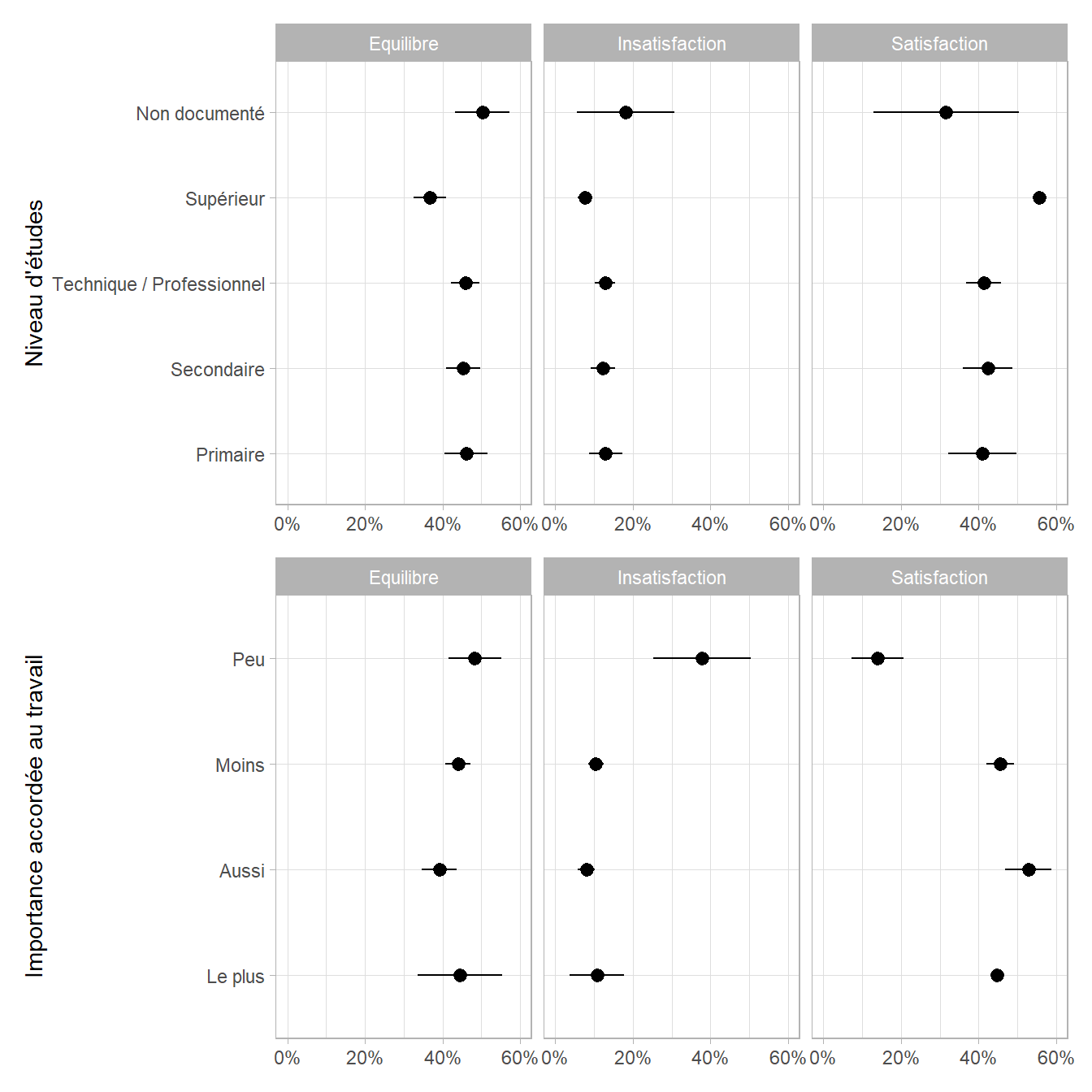
Pour faciliter l’interprétation, on pourra représenter les prédictions marginales du modèle (cf. Chapitre 24) avec broom.helpers::plot_marginal_predictions().
42.4 Données pondérées
42.4.1 avec survey::svyolr()
L’extension survey (cf. Chapitre 28) propose une fonction native survey::svyolr() pour le calcul d’une régression ordinale.
Nous allons commencer par définir le plan d’échantillonnage.
Calculons le modèle.
Le résultat peut être visualisé aisément avec gtsummary::tbl_regression() ou ggstats::ggcoef_model().
42.4.2 avec svrepmisc::svymultinom()
Alternativement, il est possible d’utiliser à ordinal::clm() en ayant recours à des poids de réplication, comme suggéré par Thomas Lumley dans son ouvrage Complex Surveys: A Guide to Analysis Using R.
L’extension svrepmisc disponible sur GitHub fournit quelques fonctions facilitant l’utilisation des poids de réplication avec survey. Pour l’installer, on utilisera le code ci-dessous :
En premier lieu, il faut définir le design de notre tableau de données puis calculer des poids de réplication.
Il faut prévoir un nombre de replicates suffisant pour calculer ultérieurement les intervalles de confiance des coefficients. Plus ce nombre est élevé, plus précise sera l’estimation de la variance et donc des valeurs p et des intervalles de confiance. Cependant, plus ce nombre est élevé, plus le temps de calcul sera important. Pour gagner en temps de calcul, nous avons ici pris une valeur de 25, mais l’usage est de considérer au moins 1000 réplications.
svrepmisc fournit une fonction svrepmisc::svyclm() pour le calcul d’une régression multinomiale avec des poids de réplication.
Warning: (-1) Model failed to converge with max|grad| = 0.000324169 (tol = 1e-06)
In addition: step factor reduced below minimumWarning: (-1) Model failed to converge with max|grad| = 0.000102733 (tol = 1e-06)
In addition: step factor reduced below minimumWarning: (-1) Model failed to converge with max|grad| = 0.000135603 (tol = 1e-06)
In addition: step factor reduced below minimumsvrepmisc fournit également des méthodes svrepmisc::confint() et svrepmisc::tidy(). Nous pouvons donc calculer et afficher les odds ratio et leur intervalle de confiance.
Coefficient SE t value Pr(>|t|)
Insatisfaction|Equilibre -2.03917466 0.60371861 -3.3777 0.004143 **
Equilibre|Satisfaction 0.27271800 0.57887328 0.4711 0.644335
sexeHomme -0.13280477 0.16774262 -0.7917 0.440866
etudesSecondaire -0.04271403 0.37404868 -0.1142 0.910599
etudesTechnique / Professionnel 0.00042809 0.30042742 0.0014 0.998882
etudesSupérieur 0.64247607 0.28577870 2.2482 0.040029 *
etudesNon documenté -0.46945975 0.68477051 -0.6856 0.503441
trav.impAussi 0.12071087 0.51117453 0.2361 0.816515
trav.impMoins 0.05267146 0.52836595 0.0997 0.921913
trav.impPeu -1.53039056 0.51739594 -2.9579 0.009776 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 2.5 % 97.5 %
Insatisfaction|Equilibre -3.32597041 -0.7523789
Equilibre|Satisfaction -0.96112118 1.5065572
sexeHomme -0.49033969 0.2247302
etudesSecondaire -0.83997992 0.7545519
etudesTechnique / Professionnel -0.63991781 0.6407740
etudesSupérieur 0.03335318 1.2515990
etudesNon documenté -1.92901354 0.9900940
trav.impAussi -0.96883185 1.2102536
trav.impMoins -1.07351390 1.1788568
trav.impPeu -2.63319391 -0.4275872 term estimate std.error statistic p.value
1 Equilibre|Satisfaction 1.3135298 0.5788733 0.471118661 0.644334643
2 etudesNon documenté 0.6253400 0.6847705 -0.685572392 0.503441383
3 etudesSecondaire 0.9581854 0.3740487 -0.114193780 0.910598668
4 etudesSupérieur 1.9011825 0.2857787 2.248159372 0.040029274
5 etudesTechnique / Professionnel 1.0004282 0.3004274 0.001424921 0.998881856
6 Insatisfaction|Equilibre 0.1301361 0.6037186 -3.377690578 0.004143161
7 sexeHomme 0.8756360 0.1677426 -0.791717511 0.440866383
8 trav.impAussi 1.1282986 0.5111745 0.236144135 0.816514956
9 trav.impMoins 1.0540833 0.5283659 0.099687462 0.921912571
10 trav.impPeu 0.2164511 0.5173959 -2.957871192 0.009775762
conf.low conf.high
1 0.38246383 4.5111729
2 0.14529145 2.6914875
3 0.43171919 2.1266583
4 1.03391564 3.4959283
5 0.52733576 1.8979493
6 0.03593763 0.4712442
7 0.61241832 1.2519848
8 0.37952612 3.3543351
9 0.34180533 3.2506560
10 0.07184862 0.6520805Par contre, le support de gtsummary::tbl_regression() et ggstats::ggcoef_model() est plus limité. Vous pourrez afficher un tableau basique des résultats et un graphiques des coefficients, mais sans les enrichissements usuels (identification des variables, étiquettes propres, identification des niveaux, etc.).
42.4.3 avec svyVGAM::svy_glm()
Une alternative possible pour le calcul de la régression logistique multinomiale avec des données pondérées est svyVGAM::svy_vglm() avec family = VGAM::multinomial.
Nous allons commencer par définir le plan d’échantillonnage.
Puis, on appelle svyVGAM::svy_vglm() en précisant family = VGAM::cumulative(parallel = TRUE).
rego7 <- svyVGAM::svy_vglm(
trav.satisf ~ sexe + etudes + trav.imp,
family = VGAM::cumulative(parallel = TRUE),
design = dw
)
rego7 |> summary()svy_vglm.survey.design(trav.satisf ~ sexe + etudes + trav.imp,
family = VGAM::cumulative(parallel = TRUE), design = dw)
Independent Sampling design (with replacement)
Called via srvyr
Sampling variables:
- ids: `1`
- weights: poids
Data variables: id (int), age (int), sexe (fct), nivetud (fct), poids (dbl),
occup (fct), qualif (fct), freres.soeurs (int), clso (fct), relig (fct),
trav.imp (fct), trav.satisf (ord), hard.rock (fct), lecture.bd (fct),
peche.chasse (fct), cuisine (fct), bricol (fct), cinema (fct), sport (fct),
heures.tv (dbl), groupe_ages (fct), etudes (fct)
Coef SE z p
(Intercept):1 -2.03917232 0.52467564 -3.8865 0.0001017
(Intercept):2 0.27272042 0.51315926 0.5315 0.5951044
sexeHomme 0.13280416 0.15421876 0.8611 0.3891602
etudesSecondaire 0.04271296 0.28498254 0.1499 0.8808599
etudesTechnique / Professionnel -0.00043004 0.25720348 -0.0017 0.9986659
etudesSupérieur -0.64247750 0.26590126 -2.4162 0.0156823
etudesNon documenté 0.46945812 0.52541495 0.8935 0.3715896
trav.impAussi -0.12071140 0.48525530 -0.2488 0.8035476
trav.impMoins -0.05267211 0.47029563 -0.1120 0.9108251
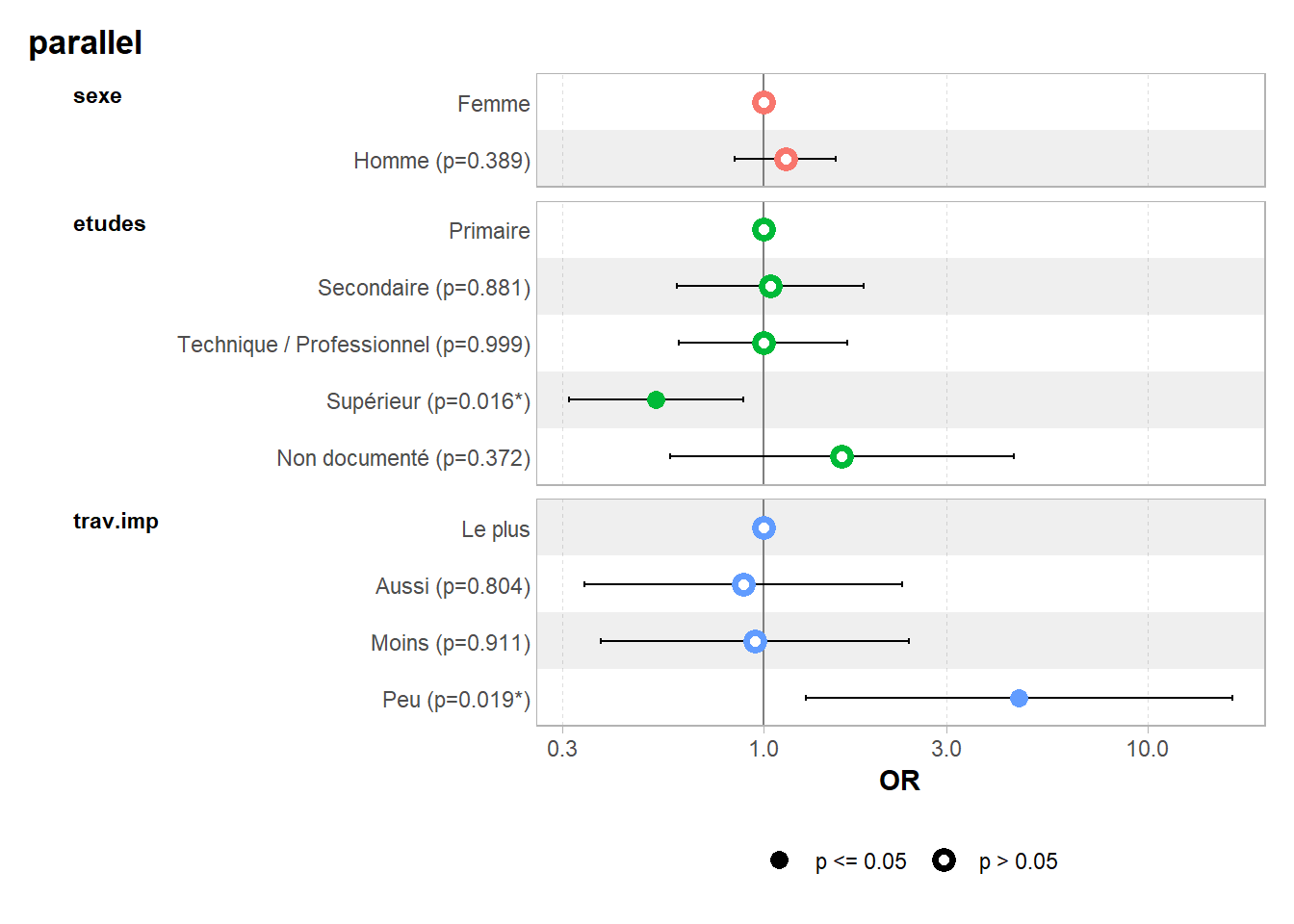
trav.impPeu 1.53036737 0.65156164 2.3488 0.0188356Là encore, le support de gtsummary::tbl_regression() et ggstats::ggcoef_model() sera limité (seulement des résultats bruts). Pour calculer les odds ratios avec leurs intervalles de confiance, on pourra avoir recours à broom.helpers::tidy_parameters().
term estimate std.error conf.level conf.low
1 (Intercept):1 0.1301364 0.06827939 0.95 0.04653653
2 (Intercept):2 1.3135330 0.67405160 0.95 0.48043985
3 sexeHomme 1.1420263 0.17612188 0.95 0.84412131
4 etudesSecondaire 1.0436383 0.29741869 0.95 0.59699738
5 etudesTechnique / Professionnel 0.9995700 0.25709290 0.95 0.60378349
6 etudesSupérieur 0.5259877 0.13986079 0.95 0.31234891
7 etudesNon documenté 1.5991274 0.84020546 0.95 0.57101702
8 trav.impAussi 0.8862897 0.43007677 0.95 0.34239361
9 trav.impMoins 0.9486910 0.44616524 0.95 0.37740568
10 trav.impPeu 4.6198737 3.01013253 0.95 1.28830837
conf.high statistic df.error p.value
1 0.3639179 -3.886538948 Inf 0.0001016836
2 3.5912276 0.531453766 Inf 0.5951043720
3 1.5450672 0.861141383 Inf 0.3891601794
4 1.8244316 0.149879202 Inf 0.8808599211
5 1.6547990 -0.001671995 Inf 0.9986659418
6 0.8857499 -2.416225817 Inf 0.0156823321
7 4.4783403 0.893499744 Inf 0.3715896094
8 2.2941709 -0.248758549 Inf 0.8035475563
9 2.3847407 -0.111997880 Inf 0.9108250872
10 16.5668669 2.348768359 Inf 0.0188356206