22 Régression logistique binaire

Dans le chapitre précédent (Chapitre 21), nous avons abordé la régression linéaire pour les variables continues. Pour analyser une variable catégorielle, il est nécessaire d’avoir recours à d’autres types de modèles. Les modèles linéaires généralisés (generalized linear models ou GLM en anglais) sont une généralisation de la régression linéaire grâce à l’utilisation d’une fonction de lien utilisée pour transformer la variable à expliquer et pouvoir ainsi retomber sur un modèle linéaire classique. Il existe de multiples fonctions de lien correspondant à tout autant de modèles. Par exemple, on pourra utiliser un modèle de Poisson pour une variable entière positive ou un modèle d’incidence.

Pour une variable binaire (c’est-à-dire du type oui / non ou vrai / faux), les modèles les plus courants utilisent les fonctions de lien probit ou logit, cette dernière fonction correspondent à la régression logistique binaire (modèle logit). Comme pour la régression linéaire, les variables explicatives peuvent être continues et/ou catégorielles.

22.1 Préparation des données

Dans ce chapitre, nous allons encore une fois utiliser les données de l’enquête Histoire de vie, fournies avec l’extension questionr.

data(hdv2003, package = "questionr")
d <- hdv2003

À titre d’exemple, nous allons étudier l’effet de l’âge, du sexe, du niveau d’étude, de la pratique religieuse et du nombre moyen d’heures passées à regarder la télévision par jour sur la probabilité de pratiquer un sport.

En premier lieu, il importe de vérifier, par exemple avec labelled::look_for(), que notre variable d’intérêt (ici sport) est correctement codée, c’est-à-dire que la première modalité correspondent à la référence (soit ne pas avoir vécu l’évènement d’intérêt) et que la seconde modalité corresponde au fait d’avoir vécu l’évènement.

library(labelled)
d |> look_for("sport")

 pos variable label col_type missing values
 19  sport    —     fct      0       Non   
                                     Oui

Dans notre exemple, la modalité Non est déjà la première modalité. Il n’y a donc pas besoin de modifier notre variable.

Il faut également la présence éventuelle de données manquantes (NA)¹. Les observations concernées seront tout simplement exclues du modèle lors de son calcul. Ce n’est pas notre cas ici.

¹ Pour visualiser le nombre de données manquantes (NA) de l’ensemble des variables d’un tableau, on pourra avoir recours à questionr::freq.na().

Astuce

Alternativement, on pourra aussi coder notre variable à expliquer sous forme booléenne (FALSE / TRUE) ou numériquement en 0/1.

Il est possible d’indiquer un facteur à plus de deux modalités. Dans une telle situation, R considérera que tous les modalités, sauf la modalité de référence, est une réalisation de la variable d’intérêt. Cela serait correct, par exemple, si notre variable sport était codée ainsi : Non, Oui, de temps en temps, Oui, régulièrement. Cependant, afin d’éviter tout risque d’erreur ou de mauvaise interprétation, il est vivement conseillé de recoder au préalable sa variable d’intérêt en un facteur à deux modalités.

La notion de modalité de référence s’applique également aux variables explicatives catégorielles. En effet, dans un modèle, tous les coefficients sont calculés par rapport à la modalité de référence (cf. Section 21.2). Il importe donc de choisir une modalité de référence qui fasse sens afin de faciliter l’interprétation. Par ailleurs, ce choix doit dépendre de la manière dont on souhaite présenter les résultats (le data storytelling est essentiel). De manière générale on évitera de choisir comme référence une modalité peu représentée dans l’échantillon ou bien une modalité correspondant à une situation atypique.

Prenons l’exemple de la variable sexe. Souhaite-t-on connaitre l’effet d’être une femme par rapport au fait d’être un homme ou bien l’effet d’être un homme par rapport au fait d’être une femme ? Si l’on opte pour le second, alors notre modalité de référence sera le sexe féminin. Comme est codée cette variable ?

d |> look_for("sexe")

 pos variable label col_type missing values
 3   sexe     —     fct      0       Homme 
                                     Femme

La modalité Femme s’avère ne pas être la première modalité. Nous devons appliquer la fonction forcats::fct_relevel() ou la fonction stats::relevel() :

library(tidyverse)
d <- d |> 
  mutate(sexe = sexe |> fct_relevel("Femme"))

d |> guideR::proportion(sexe)

# A tibble: 2 × 4
  sexe      n     N  prop
  <fct> <int> <int> <dbl>
1 Femme  1101  2000  55.0
2 Homme   899  2000  45.0

Données labellisées

Si l’on utilise des données labellisées (voir Chapitre 12), nos variables catégorielles seront stockées sous la forme d’un vecteur numérique avec des étiquettes. Il sera donc nécessaire de convertir ces variables en facteurs, tout simplement avec labelled::to_factor() ou labelled::unlabelled().

Les variables age et heures.tv sont des variables quantitatives. Il importe de vérifier qu’elles sont bien enregistrées en tant que variables numériques. En effet, il arrive parfois que dans le fichier source les variables quantitatives soient renseignées sous forme de valeur textuelle et non sous forme numérique.

d |> look_for("age", "heures")

 pos variable  label col_type missing values
 2   age       —     int      0             
 20  heures.tv —     dbl      5

Nos deux variables sont bien renseignées sous forme numérique (respectivement des entiers et des nombres décimaux).

Cependant, l’effet de l’âge est rarement linéaire. Un exemple trivial est par exemple le fait d’occuper un emploi qui sera moins fréquent aux jeunes âges et aux âges élevés. Dès lors, on pourra transformer la variable age en groupe d’âges (et donc en variable catégorielle) avec la fonction cut() (cf. Section 9.4) :

d <- d |> 
  mutate(
    groupe_ages = age |>
      cut(
        c(18, 25, 45, 65, 99),
        right = FALSE,
        include.lowest = TRUE,
        labels = c("18-24 ans", "25-44 ans",
                   "45-64 ans", "65 ans et plus")
      )
  )
d |> guideR::proportion(groupe_ages)

# A tibble: 4 × 4
  groupe_ages        n     N  prop
  <fct>          <int> <int> <dbl>
1 18-24 ans        169  2000  8.45
2 25-44 ans        706  2000 35.3 
3 45-64 ans        745  2000 37.2 
4 65 ans et plus   380  2000 19

Jetons maintenant un œil à la variable nivetud :

d |> guideR::proportion(nivetud)

# A tibble: 9 × 4
  nivetud                                                          n     N  prop
  <fct>                                                        <int> <int> <dbl>
1 N'a jamais fait d'etudes                                        39  2000  1.95
2 A arrete ses etudes, avant la derniere annee d'etudes prima…    86  2000  4.3 
3 Derniere annee d'etudes primaires                              341  2000 17.0 
4 1er cycle                                                      204  2000 10.2 
5 2eme cycle                                                     183  2000  9.15
6 Enseignement technique ou professionnel court                  463  2000 23.2 
7 Enseignement technique ou professionnel long                   131  2000  6.55
8 Enseignement superieur y compris technique superieur           441  2000 22.0 
9 <NA>                                                           112  2000  5.6

En premier lieu, cette variable est détaillée en pas moins de huit modalités dont certaines sont peu représentées (seulement 39 individus soit 2 % n’ont jamais fait d’études par exemple). Afin d’améliorer notre modèle logistique, il peut être pertinent de regrouper certaines modalités (cf. Section 9.3) :

d <- d |> 
  mutate(
    etudes = nivetud |> 
      fct_recode(
      "Primaire" = "N'a jamais fait d'etudes",
      "Primaire" = "A arrete ses etudes, avant la derniere annee d'etudes primaires",
      "Primaire" = "Derniere annee d'etudes primaires",
      "Secondaire" = "1er cycle",
      "Secondaire" = "2eme cycle",
      "Technique / Professionnel" = "Enseignement technique ou professionnel court",
      "Technique / Professionnel" = "Enseignement technique ou professionnel long",
      "Supérieur" = "Enseignement superieur y compris technique superieur"
    )    
  )
d |> guideR::proportion(etudes)

# A tibble: 5 × 4
  etudes                        n     N  prop
  <fct>                     <int> <int> <dbl>
1 Primaire                    466  2000  23.3
2 Secondaire                  387  2000  19.4
3 Technique / Professionnel   594  2000  29.7
4 Supérieur                   441  2000  22.0
5 <NA>                        112  2000   5.6

Notre variable comporte également 112 individus avec une valeur manquante. Si nous conservons cette valeur manquante, ces 112 individus seront, par défaut, exclus de l’analyse. Ces valeurs manquantes n’étant pas négligeable (5,6 %), nous pouvons également faire le choix de considérer ces valeurs manquantes comme une modalité supplémentaire. Auquel cas, nous utiliserons la fonction forcats::fct_na_value_to_level() :

d$etudes <- d$etudes |> 
  fct_na_value_to_level("Non documenté")
d |> guideR::proportion(etudes)

# A tibble: 5 × 4
  etudes                        n     N  prop
  <fct>                     <int> <int> <dbl>
1 Primaire                    466  2000  23.3
2 Secondaire                  387  2000  19.4
3 Technique / Professionnel   594  2000  29.7
4 Supérieur                   441  2000  22.0
5 Non documenté               112  2000   5.6

Enfin, pour améliorer les différentes sorties (tableaux et figures), nous allons ajouter des étiquettes de variables (cf. Chapitre 11) avec labelled::set_variable_labels().

d <- d |> 
  set_variable_labels(
    sport = "Pratique un sport ?",
    sexe = "Sexe",
    groupe_ages = "Groupe d'âges",
    etudes = "Niveau d'études",
    relig = "Rapport à la religion",
    heures.tv = "Heures de télévision / jour"
  )

Code récapitulatif (préparation des données)

data(hdv2003, package = "questionr")
d <-
  hdv2003 |> 
  mutate(
    sexe = sexe |> fct_relevel("Femme"),
    groupe_ages = age |>
      cut(
        c(18, 25, 45, 65, 99),
        right = FALSE,
        include.lowest = TRUE,
        labels = c("18-24 ans", "25-44 ans",
                   "45-64 ans", "65 ans et plus")
      ),
    etudes = nivetud |> 
      fct_recode(
        "Primaire" = "N'a jamais fait d'etudes",
        "Primaire" = "A arrete ses etudes, avant la derniere annee d'etudes primaires",
        "Primaire" = "Derniere annee d'etudes primaires",
        "Secondaire" = "1er cycle",
        "Secondaire" = "2eme cycle",
        "Technique / Professionnel" = "Enseignement technique ou professionnel court",
        "Technique / Professionnel" = "Enseignement technique ou professionnel long",
        "Supérieur" = "Enseignement superieur y compris technique superieur"
    ) |> 
    fct_na_value_to_level("Non documenté")  
  ) |> 
  set_variable_labels(
    sport = "Pratique un sport ?",
    sexe = "Sexe",
    groupe_ages = "Groupe d'âges",
    etudes = "Niveau d'études",
    relig = "Rapport à la religion",
    heures.tv = "Heures de télévision / jour"
  )

22.2 Statistiques descriptives

Avant toute analyse multivariable, il est toujours bon de procéder à une analyse descriptive bivariée simple, tout simplement avec gtsummary::tbl_summary(). Dans le cas présent, il est préférable d’afficher les pourcentages en ligne qui permettent ainsi de comparer de suite la proportion de personnes faisant du sport entre les différentes catégories.

Ajoutons quelques tests de comparaison avec gtsummary::add_p(). Petite astuce : gtsummary::modify_spanning_header() permet de rajouter un en-tête sur plusieurs colonnes.

library(gtsummary)
theme_gtsummary_language("fr", decimal.mark = ",", big.mark = " ")

d |> 
  tbl_summary(
    by = sport,
    include = c(sexe, groupe_ages, etudes, relig, heures.tv),
    percent = "row"
  ) |>
  add_overall(last = TRUE) |> 
  add_p() |> 
  bold_labels() |> 
  modify_spanning_header(
    all_stat_cols(stat_0 = FALSE) ~ "**Pratique un sport ?**"
  )

Caractéristique	Pratique un sport ?		Overall N = 2 000¹	p-valeur²
Caractéristique	Non N = 1 277¹	Oui N = 723¹	Overall N = 2 000¹	p-valeur²
Sexe				<0,001
Femme	747 (68%)	354 (32%)	1 101 (100%)
Homme	530 (59%)	369 (41%)	899 (100%)
Groupe d'âges				<0,001
18-24 ans	58 (34%)	111 (66%)	169 (100%)
25-44 ans	359 (51%)	347 (49%)	706 (100%)
45-64 ans	541 (73%)	204 (27%)	745 (100%)
65 ans et plus	319 (84%)	61 (16%)	380 (100%)
Niveau d'études				<0,001
Primaire	416 (89%)	50 (11%)	466 (100%)
Secondaire	270 (70%)	117 (30%)	387 (100%)
Technique / Professionnel	378 (64%)	216 (36%)	594 (100%)
Supérieur	186 (42%)	255 (58%)	441 (100%)
Non documenté	27 (24%)	85 (76%)	112 (100%)
Rapport à la religion				0,14
Pratiquant regulier	182 (68%)	84 (32%)	266 (100%)
Pratiquant occasionnel	295 (67%)	147 (33%)	442 (100%)
Appartenance sans pratique	473 (62%)	287 (38%)	760 (100%)
Ni croyance ni appartenance	239 (60%)	160 (40%)	399 (100%)
Rejet	60 (65%)	33 (35%)	93 (100%)
NSP ou NVPR	28 (70%)	12 (30%)	40 (100%)
Heures de télévision / jour	2,00 (1,00 – 3,00)	2,00 (1,00 – 3,00)	2,00 (1,00 – 3,00)	<0,001
Manquant	2	3	5
¹ n (%); Médiane (Q1 – Q3)
² test du khi-deux d’indépendance; test de Wilcoxon-Mann-Whitney

Table 22.1: Pratique d’un sport selon différentes variables explicatives (analyse bivariée)

Comparer visuellement une proportion entre sous-groupes

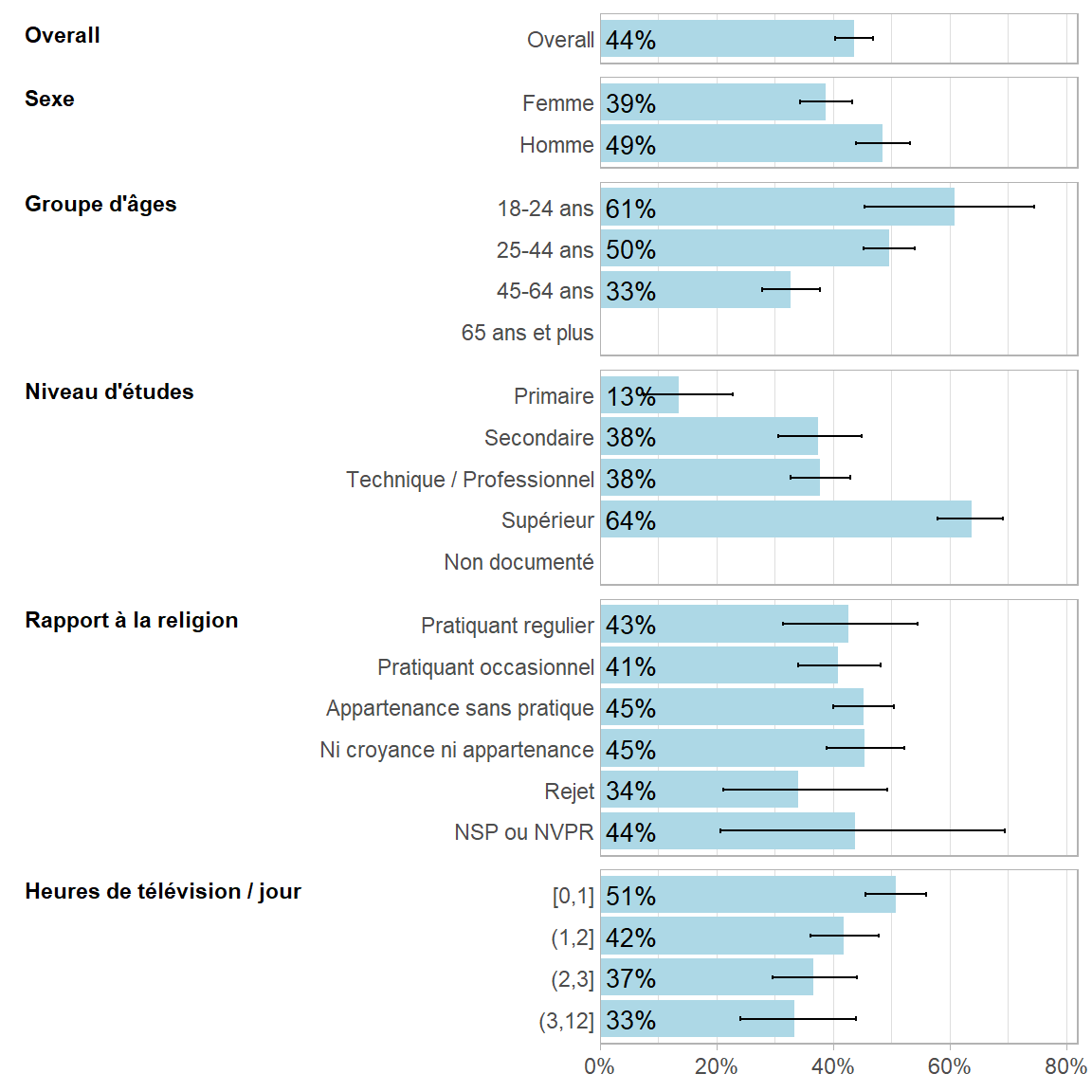
Dans ses versions récentes, guideR, le package compagnon de guide-R, propose une fonction guideR::plot_proportions() qui permet de comparer facilement les proportions selon plusieurs sous-groupes, en affichant également les intervalles de confiance et les p-valeurs (test de Fisher par défaut). Il est également possible de lui passer une variable explicative continue, qui sera alors automatiquement convertie en quartiles.

d |> 
  guideR::plot_proportions(
    sport == "Oui",
    by = c(sexe, groupe_ages, etudes, relig, heures.tv),
    fill = "lightblue",
    flip = TRUE
  )

Warning: There were 2 warnings in `dplyr::mutate()`.
The first warning was:
ℹ In argument: `.ci_prop(...)`.
ℹ In row 9.
Caused by warning in `stats::prop.test()`:
! L’approximation du Chi-2 est peut-être incorrecte
ℹ Run `dplyr::last_dplyr_warnings()` to see the 1 remaining warning.

22.3 Calcul de la régression logistique binaire

La spécification d’une régression logistique se fait avec stats::glm() et est très similaire à celle d’une régression linéaire simple (cf. Section 21.3) : on indique la variable à expliquer suivie d’un tilde (~) puis des variables explicatives séparées par un plus (+)². Il faut indiquer à glm() la famille du modèle souhaité : on indiquera simplement family = binomial pour un modèle logit³.

² Il est possible de spécifier des modèles plus complexes, notamment avec des effets d’interaction, qui seront aborder plus loin (cf. Chapitre 26).

³ Pour un modèle probit, on indiquera family = binomial("probit").

mod <- glm(
  sport ~ sexe + groupe_ages + etudes + relig + heures.tv,
  family = binomial,
  data = d
)

Pour afficher les résultats du modèle, le plus simple est d’avoir recours à gtsummary::tbl_regression().

mod |> 
  tbl_regression(intercept = TRUE) |> 
  bold_labels()

Caractéristique	log(OR)	95% IC	p-valeur
(Intercept)	-0,80	-1,4 – -0,17	0,014
Sexe
Femme	—	—
Homme	0,44	0,23 – 0,65	<0,001
Groupe d'âges
18-24 ans	—	—
25-44 ans	-0,42	-0,87 – 0,03	0,065
45-64 ans	-1,1	-1,6 – -0,62	<0,001
65 ans et plus	-1,4	-1,9 – -0,85	<0,001
Niveau d'études
Primaire	—	—
Secondaire	0,95	0,57 – 1,3	<0,001
Technique / Professionnel	1,0	0,68 – 1,4	<0,001
Supérieur	1,9	1,5 – 2,3	<0,001
Non documenté	2,2	1,5 – 2,8	<0,001
Rapport à la religion
Pratiquant regulier	—	—
Pratiquant occasionnel	-0,02	-0,39 – 0,35	>0,9
Appartenance sans pratique	-0,01	-0,35 – 0,34	>0,9
Ni croyance ni appartenance	-0,22	-0,59 – 0,16	0,3
Rejet	-0,38	-0,95 – 0,17	0,2
NSP ou NVPR	-0,08	-0,92 – 0,70	0,8
Heures de télévision / jour	-0,12	-0,19 – -0,06	<0,001
Abréviations: IC = intervalle de confiance, OR = rapport de cotes

Table 22.2: Facteurs associés à la pratique d’un sport (régression logistique binaire)

22.4 Interpréter les coefficients

L’intercept traduit la situation à la référence (i.e. toutes les variables catégorielles à leur modalité de référence et les variables continues à 0), après transformation selon la fonction de lien (i.e. après la transformation logit).

Illustrons cela. Supposons donc une personne de sexe féminin, âgée entre 18 et 24 ans, de niveau d’étude primaire, pratiquante régulière et ne regardant pas la télévision (situation de référence). Seul l’intercept s’applique dans le modèle, et donc le modèle prédit que sa probabilité de faire du sport est de \(-0,80\) selon l’échelle logit. Retraduisons cela en probabilité classique avec la fonction logit inverse.

logit_inverse <- binomial("logit") |> purrr::pluck("linkinv")
logit_inverse(-0.80)

[1] 0.3100255

Selon le modèle, la probabilité que cette personne fasse du sport est donc de \(31\%\).

Prenons maintenant une personne identique mais de sexe masculin. Nous devons donc considérer, en plus de l’intercept, le coefficient associé à la modalité Homme. Sa probabilité de faire du sport est donc :

logit_inverse(-0.80 + 0.44)

[1] 0.4109596

Le coefficient associé à Homme est donc un modificateur par rapport à la situation de référence.

Enfin, considérons que cette dernière personne regarde également la télévision 2 heures en moyenne par jour. Nous devons alors considérer le coefficient associé à la variable heures.tv et, comme il s’agit d’une variable continue, multiplier ce coefficient par 2, car le coefficient représente le changement pour un incrément de 1 unité.

logit_inverse(-0.80 + 0.44 + 2 * -0.12)

[1] 0.3543437

Il est crucial de bien comprendre comment dans quels cas et comment chaque coefficient est utilisé par le modèle.

Le package {breakdown} permet de mieux visualiser notre dernier exemple.

individu3 <- d[1, ]
individu3$sexe[1] <- "Homme"
individu3$groupe_ages[1] <- "18-24 ans"
individu3$etudes[1] <- "Primaire"
individu3$relig[1] <- "Pratiquant regulier"
individu3$heures.tv[1] <- 2

library(breakDown)
logit <- function(x) exp(x) / (1 + exp(x))
plot(
  broken(mod, individu3, predict.function = betas),
  trans = logit
) +
  scale_y_continuous(
    labels = scales::label_percent(),
    breaks = 0:5/5,
    limits = c(0, 1)
  )

Décomposition de la probabilité de faire du sport de l’individu 3

22.5 La notion d’odds ratio

L’un des intérêts de la régression logistique logit réside dans le fait que l’exponentiel des coefficients correspond à des odds ratio ou rapport des côtes en français.

Astuce

Pour comprendre la notion de côte (odd en anglais), on peut se référer aux paris sportifs. Par exemple, lorsque les trois quarts des parieurs parient que le cheval A va remporter la course, on dit alors que ce cheval à une côte de trois contre un (trois personnes parient qu’il va gagner contre une personne qu’il va perdre). Prenons un autre cheval : si les deux tiers pensent que le cheval B va perdre (donc un tiers pense qu’il va gagner), on dira alors que sa côte est de un contre deux (une personne pense qu’il va gagner contre deux qu’il va perdre).

Si l’on connait la proportion ou probabilité p d’avoir vécu ou de vivre un évènement donné (ici gagner la course), la côte (l’odd) s’obtient avec la formule suivante : \(p/(1-p)\). La côte du cheval A est bien \(0,75/(1-0,75)=0,75/0,25=3\) est celle du cheval B \((1/3)/(2/3)=1/2=0,5\).

Pour comparer deux côtes (par exemple pour savoir si le cheval A a une probabilité plus élevée de remporter la course que le cheval B, selon les parieurs), on calculera tout simplement le rapport des côtes ou odds ratio (OR) : \(OR_{A/B}=Odds_{A}/Odds_{B}=3/0,5=6\).

Ce calcul peut se faire facilement dans R avec la fonction questionr::odds.ratio().

questionr::odds.ratio(.75, 1/3)

[1] 6

L’odds ratio est donc égal à 1 si les deux côtes sont identiques, est supérieur à 1 si le cheval A une probabilité supérieure à celle du cheval B, et inférieur à 1 si c’est probabilité est inférieure.

On le voit, par construction, l’odds ratio de B par rapport à A est l’inverse de celui de A par rapport à B : \(OR_{B/A}=1/OR_{A/B}\).

Pour afficher les odds ratio il suffit d’indiquer exponentiate = TRUE à gtsummary::tbl_regression().

mod |> 
  tbl_regression(exponentiate = TRUE) |> 
  bold_labels()

Caractéristique	OR	95% IC	p-valeur
Sexe
Femme	—	—
Homme	1,55	1,26 – 1,91	<0,001
Groupe d'âges
18-24 ans	—	—
25-44 ans	0,66	0,42 – 1,03	0,065
45-64 ans	0,34	0,21 – 0,54	<0,001
65 ans et plus	0,25	0,15 – 0,43	<0,001
Niveau d'études
Primaire	—	—
Secondaire	2,59	1,77 – 3,83	<0,001
Technique / Professionnel	2,86	1,98 – 4,17	<0,001
Supérieur	6,63	4,55 – 9,80	<0,001
Non documenté	8,59	4,53 – 16,6	<0,001
Rapport à la religion
Pratiquant regulier	—	—
Pratiquant occasionnel	0,98	0,68 – 1,42	>0,9
Appartenance sans pratique	0,99	0,71 – 1,40	>0,9
Ni croyance ni appartenance	0,81	0,55 – 1,18	0,3
Rejet	0,68	0,39 – 1,19	0,2
NSP ou NVPR	0,92	0,40 – 2,02	0,8
Heures de télévision / jour	0,89	0,83 – 0,95	<0,001
Abréviations: IC = intervalle de confiance, OR = rapport de cotes

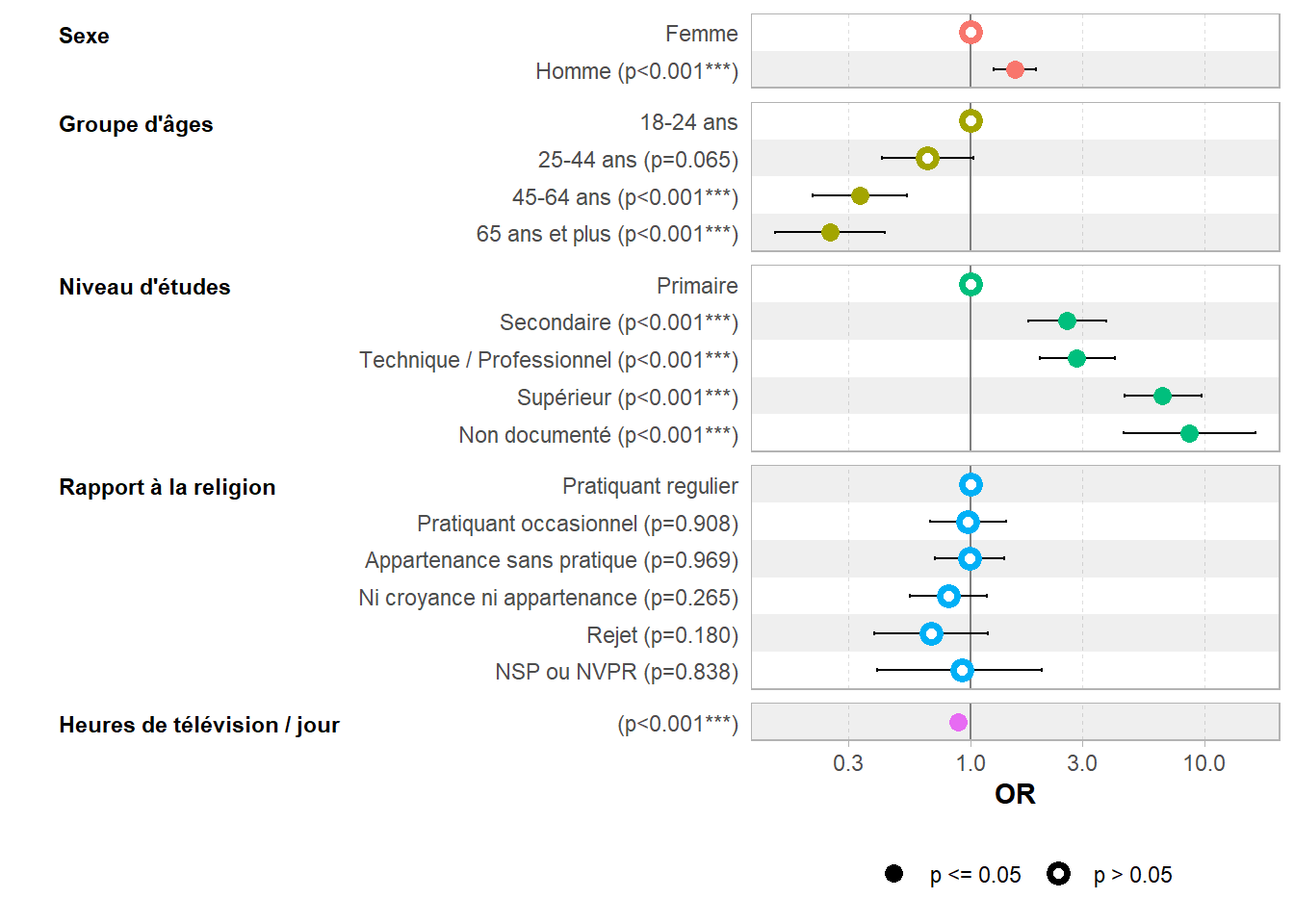
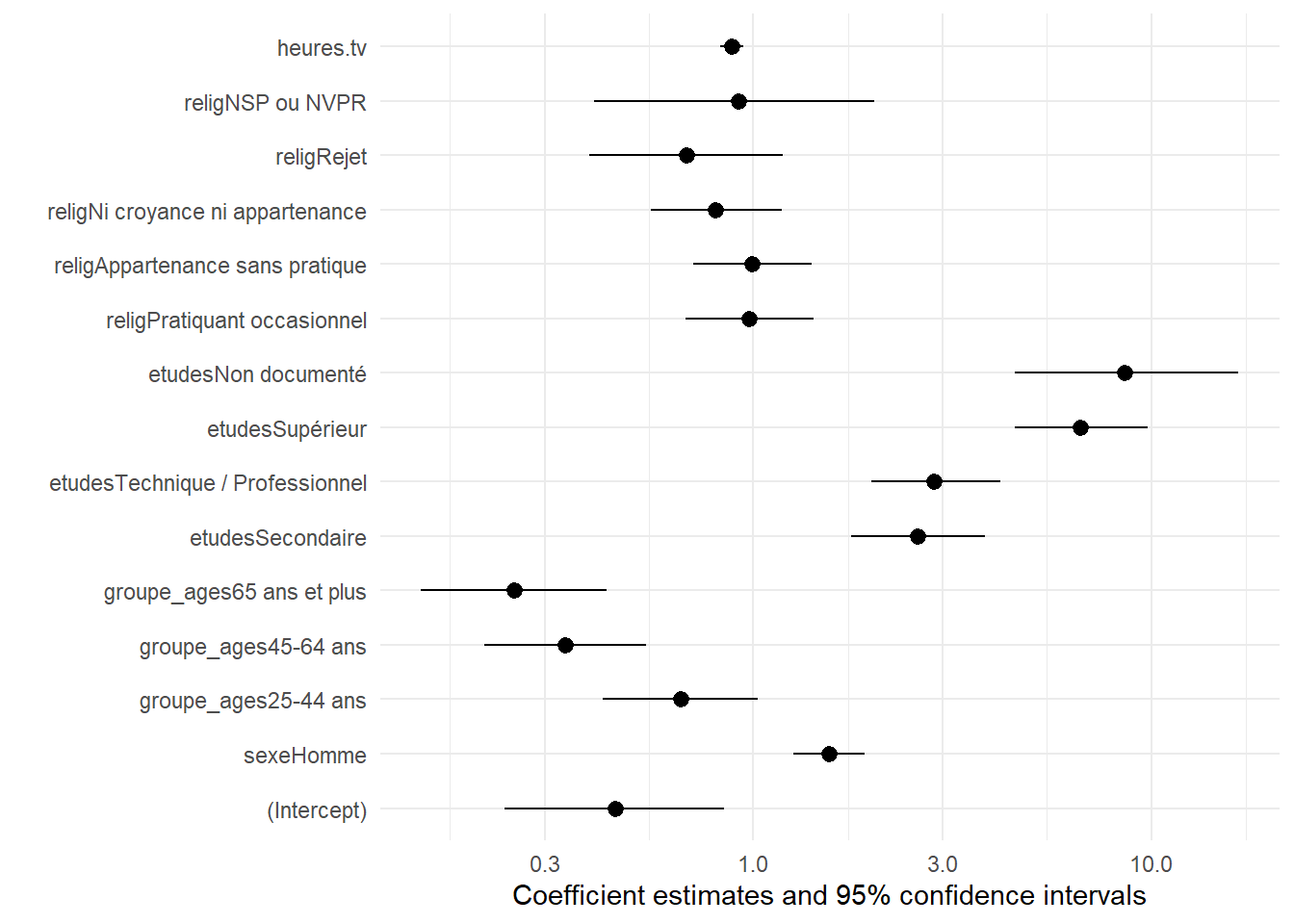
Table 22.3: Facteurs associés à la pratique d’un sport (odds ratios)

Pour une représentation visuelle, graphique en forêt ou forest plot en anglais, on aura tout simplement recours à ggstats::ggcoef_model().

mod |> 
  ggstats::ggcoef_model(exponentiate = TRUE)

Figure 22.1: Facteurs associés à la pratique d’un sport (*forest plot*)

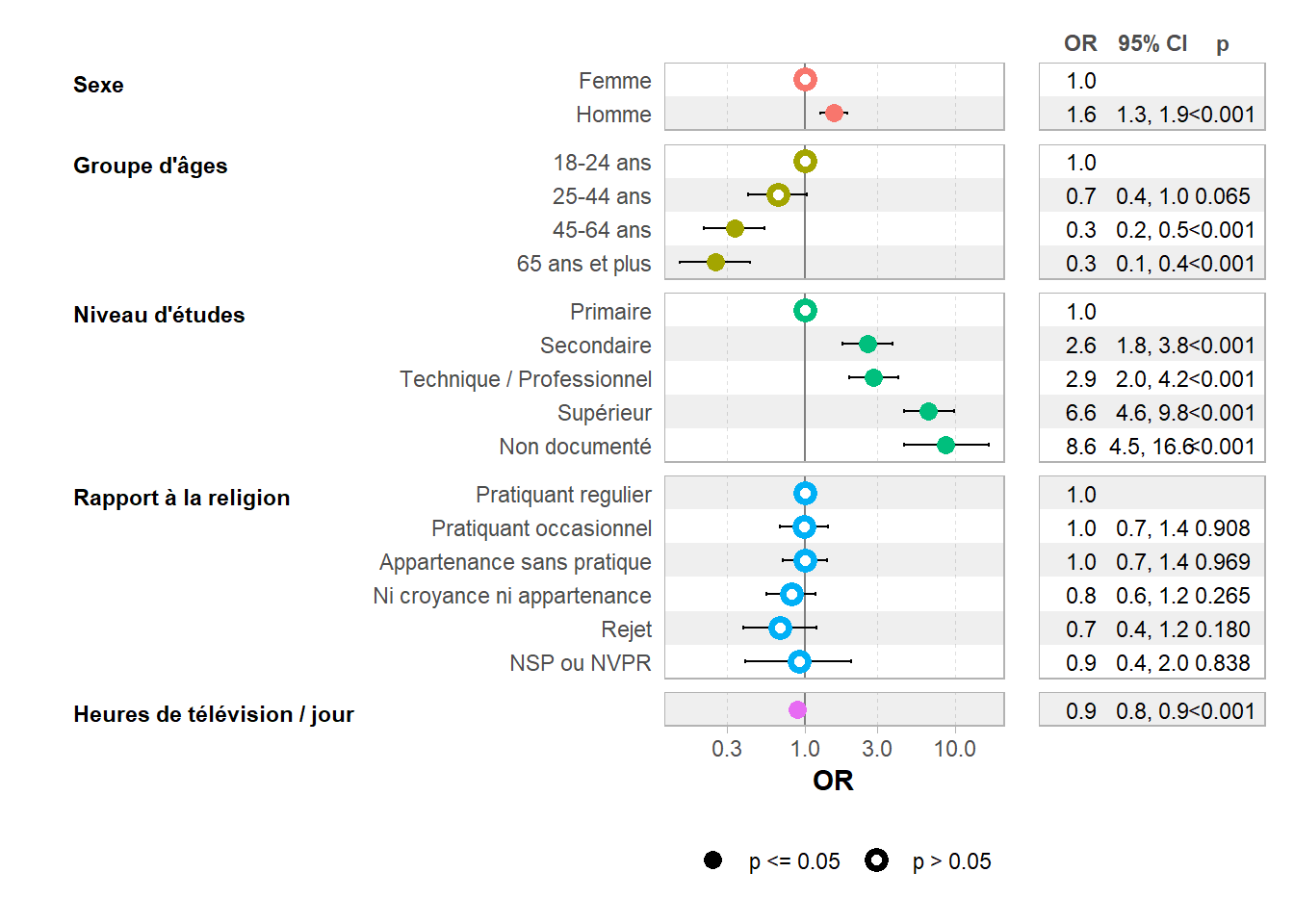
On pourra alternativement préférer ggstats::ggcoef_table()⁴ qui affiche un tableau des coefficients à la droite du forest plot.

⁴ ggstats::ggcoef_table() est disponible à partir de la version 0.4.0 de ggstats.

mod |> 
  ggstats::ggcoef_table(exponentiate = TRUE)

Figure 22.2: Facteurs associés à la pratique d’un sport (*forest plot* avec table des coefficients)

Note

Lorsque l’on réalise un forest plot de coefficients exponentialisés tels que des odds ratios, une bonne pratique consiste à utiliser une échelle logarithmique. En effet, l’inverse d’un odds ratio de 2 est 0,5. Avec une échelle logarithmique, la distance entre 0,5 et 1 est égale à celle entre 1 et 2. Sur la figure précédente, vous pourrez noter que ggstats::ggcoef_model() applique automatiquement une échelle logarithmique lorsque exponentiate = TRUE.

Quelques références : Forest Plots: Linear or Logarithmic Scale? ou encore Graphing Ratio Measures on Forest Plot.

Mise en garde

En rédigeant les résultats de la régression, il faudra être vigilant à ne pas confondre les odds ratios avec des prevalence ratios. Avec un odds ratio de 1,55, il serait tentant d’écrire que les hommes ont une probabilité 55% supérieure de pratique un sport que les femmes (toutes choses égales par ailleurs). Une telle formulation correspond à un prevalence ratio (rapport des prévalences en français) ou risk ratio (rapport des risques), à savoir diviser la probabilité de faire du sport des hommes par celle des femmes, \(p_{hommes}/p_{femmes}\). Or, cela ne correspond pas à la formule de l’odds ratio, à savoir \((p_{hommes}/(1-p_{hommes}))/(p_{femmes}/(1-p_{femmes}))\).

Lorsque le phénomène étudié est rare et donc que les probabilités sont faibles (inférieures à quelques pour-cents), alors il est vrai que les odds ratio sont approximativement égaux aux prevalence ratios. Mais ceci n’est plus du tout vrai pour des phénomènes plus fréquents.

22.6 Afficher les écarts-types plutôt que les intervalles de confiance

La manière de présenter les résultats d’un modèle de régression varie selon les disciplines, les champs thématiques et les revues. Si en sociologie et épidémiologie on aurait plutôt tendance à afficher les odds ratio avec leur intervalle de confiance, il est fréquent en économétrie de présenter plutôt les coefficients bruts et leurs écarts-types (standard deviation ou sd en anglais). De même, plutôt que d’ajouter une colonne avec les p valeurs, un usage consiste à afficher des étoiles de significativité à la droite des coefficients significatifs.

Pour cela, on pourra personnaliser le tableau produit avec gtsummary::tbl_regression(), notamment avec gtsummary::add_significance_stars() pour l’ajout des étoiles de significativité, ainsi que gtsummary::modify_column_hide() et gtsummary::modify_column_unhide() pour afficher / masquer les colonnes du tableau produit⁵.

⁵ La liste des colonnes disponibles peut être obtenues avec mod |> tbl_regression() |> purrr::pluck("table_body") |> colnames().

mod |> 
  tbl_regression() |> 
  add_significance_stars() |> 
  modify_column_hide(c("ci", "p.value")) |> 
  modify_column_unhide("std.error") |> 
  bold_labels()

Warning: Use of the "ci" column was deprecated in gtsummary v2.0, and the column will
eventually be removed from the tables.
! Review `?deprecated_ci_column()` for details on how to update your code.
ℹ The "ci" column has been replaced by the merged "conf.low" and "conf.high"
  columns (merged with `modify_column_merge()`).
ℹ In most cases, a simple update from `ci = 'a new label'` to `conf.low = 'a
  new label'` is sufficient.

Caractéristique	log(OR)¹	ET
Sexe
Femme	—	—
Homme	0,44***	0,106
Groupe d'âges
18-24 ans	—	—
25-44 ans	-0,42	0,228
45-64 ans	-1,1***	0,238
65 ans et plus	-1,4***	0,274
Niveau d'études
Primaire	—	—
Secondaire	0,95***	0,197
Technique / Professionnel	1,0***	0,190
Supérieur	1,9***	0,195
Non documenté	2,2***	0,330
Rapport à la religion
Pratiquant regulier	—	—
Pratiquant occasionnel	-0,02	0,189
Appartenance sans pratique	-0,01	0,175
Ni croyance ni appartenance	-0,22	0,193
Rejet	-0,38	0,286
NSP ou NVPR	-0,08	0,411
Heures de télévision / jour	-0,12***	0,034
Abréviations: ET = écart-type, IC = intervalle de confiance, OR = rapport de cotes
¹ p<0.05; p<0.01; **p<0.001

Table 22.4: Présentation économétrique des facteurs associés à la pratique d’un sport

Les économistes pourraient préférer le package modelsummary à gtsummary. Ces deux packages ont un objectif similaire (la production de tableaux statistiques) mais abordent cet objectif avec des approches différentes. Il faut noter que modelsummary::modelsummary() n’affiche pas les modalités de référence, ni les étiquettes de variable.

mod |> modelsummary::modelsummary(stars = TRUE)

	(1)
+ p < 0.1, * p < 0.05, p < 0.01, * p < 0.001
(Intercept)	-0.798*
	(0.324)
sexeHomme	0.440***
	(0.106)
groupe_ages25-44 ans	-0.420+
	(0.228)
groupe_ages45-64 ans	-1.085***
	(0.238)
groupe_ages65 ans et plus	-1.381***
	(0.274)
etudesSecondaire	0.951***
	(0.197)
etudesTechnique / Professionnel	1.049***
	(0.190)
etudesSupérieur	1.892***
	(0.195)
etudesNon documenté	2.150***
	(0.330)
religPratiquant occasionnel	-0.022
	(0.189)
religAppartenance sans pratique	-0.007
	(0.175)
religNi croyance ni appartenance	-0.215
	(0.193)
religRejet	-0.384
	(0.286)
religNSP ou NVPR	-0.084
	(0.411)
heures.tv	-0.121***
	(0.034)
Num.Obs.	1995
AIC	2236.2
BIC	2320.1
Log.Lik.	-1103.086
F	21.691
RMSE	0.43

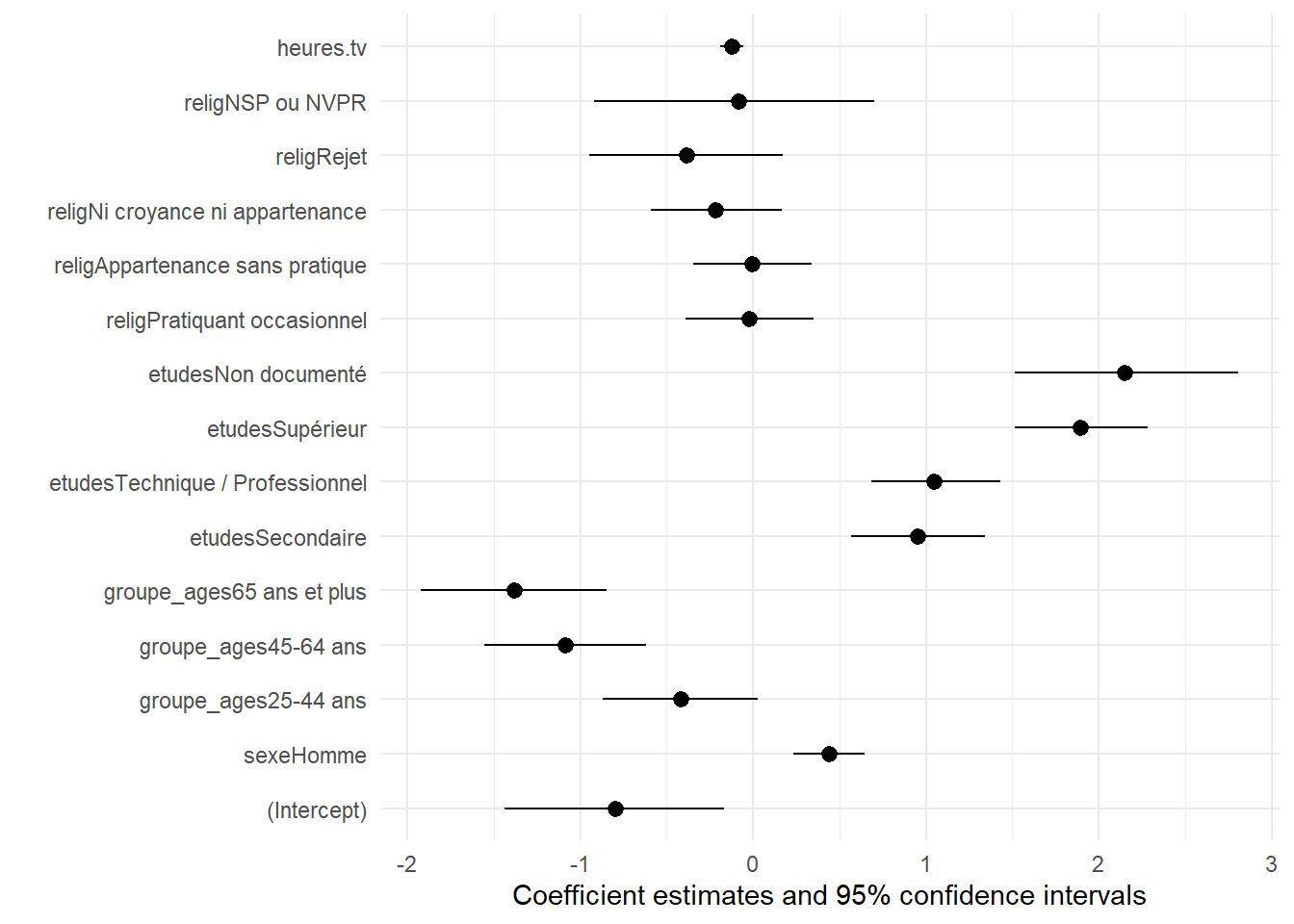
Table 22.5: Présentation des facteurs associés à la pratique d’un sport avec modelsummary()

La fonction modelsummary::modelplot() permet d’afficher un graphique des coefficients.

mod |> modelsummary::modelplot()

Figure 22.3: Facteurs associés à la pratique d’un sport avec modelplot()

ATTENTION : si l’on affiche les odds ratio avec exponentiate = TRUE, modelsummary::modelplot() conserve par défaut une échelle linéaire. On sera donc vigilant à appliquer ggplot2::scale_x_log10() manuellement pour utiliser une échelle logarithmique.

mod |>
  modelsummary::modelplot(exponentiate = TRUE) +
  ggplot2::scale_x_log10()

Figure 22.4: Odds Ratios associés à la pratique d’un sport avec modelplot()

22.7 Afficher toutes les comparaisons (pairwise contrasts)

Dans le tableau des résultats (Table 22.3), pour les variables catégorielles, il importe de bien garder en mémoire que chaque odds ratio doit se comparer à la valeur de référence. Ainsi, les odds ratios affichés pour chaque classe d’âges correspondent à une comparaison avec la classe d’âges de références, les 18-24 ans. La p-valeur associée nous indique quant à elle si cet odds ratio est significativement de 1, donc si cette classe d’âges données se comporte différemment de celle de référence.

Mais cela ne nous dit nullement si les 65 ans et plus diffèrent des 45-64 ans. Il est tout à fait possible de recalculer l’odds ratio correspondant en rapport les odds ratio à la référence : \(OR_{65+/45-64}=OR_{65+/18-24}/OR_{45-64/18-24}\).

Le package emmeans et sa fonction emmeans::emmeans() permettent de recalculer toutes les combinaisons d’odds ratio (on parle alors de pairwise contrasts) ainsi que leur intervalle de confiance et la p-valeur correspondante.

On peut ajouter facilement⁶ cela au tableau produit avec gtsummary::tbl_regression() en ajoutant l’option add_pairwise_contrasts = TRUE.

⁶ Cela nécessite néanmoins au minimum la version 1.11.0 du package broom.helpers et la version 1.6.3 de gtsummary.

mod |> 
  tbl_regression(
    exponentiate = TRUE,
    add_pairwise_contrasts = TRUE
  ) |> 
  bold_labels()

Caractéristique	OR	95% IC	p-valeur
Sexe
Homme / Femme	1,55	1,26 – 1,91	<0,001
Groupe d'âges
(25-44 ans) / (18-24 ans)	0,66	0,37 – 1,18	0,3
(45-64 ans) / (18-24 ans)	0,34	0,18 – 0,62	<0,001
(45-64 ans) / (25-44 ans)	0,51	0,38 – 0,70	<0,001
65 ans et plus / (18-24 ans)	0,25	0,12 – 0,51	<0,001
65 ans et plus / (25-44 ans)	0,38	0,24 – 0,61	<0,001
65 ans et plus / (45-64 ans)	0,74	0,47 – 1,17	0,3
Niveau d'études
Secondaire / Primaire	2,59	1,51 – 4,43	<0,001
(Technique / Professionnel) / Primaire	2,86	1,70 – 4,79	<0,001
(Technique / Professionnel) / Secondaire	1,10	0,74 – 1,64	>0,9
Supérieur / Primaire	6,63	3,89 – 11,3	<0,001
Supérieur / Secondaire	2,56	1,69 – 3,88	<0,001
Supérieur / (Technique / Professionnel)	2,32	1,61 – 3,36	<0,001
Non documenté / Primaire	8,59	3,49 – 21,1	<0,001
Non documenté / Secondaire	3,32	1,46 – 7,53	<0,001
Non documenté / (Technique / Professionnel)	3,01	1,38 – 6,56	0,001
Non documenté / Supérieur	1,30	0,58 – 2,90	>0,9
Rapport à la religion
Pratiquant occasionnel / Pratiquant regulier	0,98	0,57 – 1,68	>0,9
Appartenance sans pratique / Pratiquant regulier	0,99	0,60 – 1,63	>0,9
Appartenance sans pratique / Pratiquant occasionnel	1,02	0,68 – 1,52	>0,9
Ni croyance ni appartenance / Pratiquant regulier	0,81	0,47 – 1,40	0,9
Ni croyance ni appartenance / Pratiquant occasionnel	0,82	0,52 – 1,31	0,8
Ni croyance ni appartenance / Appartenance sans pratique	0,81	0,54 – 1,21	0,7
Rejet / Pratiquant regulier	0,68	0,30 – 1,54	0,8
Rejet / Pratiquant occasionnel	0,70	0,33 – 1,49	0,8
Rejet / Appartenance sans pratique	0,69	0,33 – 1,41	0,7
Rejet / Ni croyance ni appartenance	0,85	0,40 – 1,79	>0,9
NSP ou NVPR / Pratiquant regulier	0,92	0,29 – 2,97	>0,9
NSP ou NVPR / Pratiquant occasionnel	0,94	0,30 – 2,92	>0,9
NSP ou NVPR / Appartenance sans pratique	0,93	0,30 – 2,82	>0,9
NSP ou NVPR / Ni croyance ni appartenance	1,14	0,37 – 3,55	>0,9
NSP ou NVPR / Rejet	1,35	0,37 – 4,88	>0,9
Heures de télévision / jour	0,89	0,83 – 0,95	<0,001
Abréviations: IC = intervalle de confiance, OR = rapport de cotes

Table 22.6: Facteurs associés à la pratique d’un sport (pairwise contrasts)

De même, on peur visualiser les coefficients avec la même option dans ggstats::ggcoef_model()⁷. On peut d’ailleurs choisir les variables concernées avec l’argument pairwise_variables.

⁷ Cela nécessite néanmoins au minimum la version 1.11.0 du package broom.helpers et la version 0.2.0 de ggstats.

mod |> 
  ggstats::ggcoef_model(
    exponentiate = TRUE,
    add_pairwise_contrasts = TRUE,
    pairwise_variables = c("groupe_ages", "etudes")
  )

Figure 22.5: Facteurs associés à la pratique d’un sport (*pairwise contrasts*)

22.8 Identifier les variables ayant un effet significatif

Pour les variables catégorielles à trois modalités ou plus, les p-valeurs associées aux odds ratios nous indique si un odd ratio est significativement différent de 1, par rapport à la modalité de référence. Mais cela n’indique pas si globalement une variable a un effet significatif sur le modèle. Pour tester l’effet global d’une variable, on peut avoir recours à la fonction car::Anova(). Cette dernière va tour à tour supprimer chaque variable du modèle et réaliser une analyse de variance (ANOVA) pour voir si la variance change significativement.

car::Anova(mod)

Analysis of Deviance Table (Type II tests)

Response: sport
            LR Chisq Df Pr(>Chisq)    
sexe          17.309  1  3.176e-05 ***
groupe_ages   52.803  3  2.020e-11 ***
etudes       123.826  4  < 2.2e-16 ***
relig          4.232  5  0.5165401    
heures.tv     13.438  1  0.0002465 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ainsi, dans le cas présent, la suppression de la variable relig ne modifie significativement pas le modèle, indiquant l’absence d’effet de cette variable.

Si l’on a recours à gtsummary::tbl_regression(), on peut facilement ajouter les p-valeurs globales avec gtsummary::add_global_p()⁸.

⁸ Si l’on veut conserver les p-valeurs individuelles associées à chaque odds ratio, on ajoutera l’option keep = TRUE.

mod |>
  tbl_regression(exponentiate = TRUE) |>
  bold_labels() |> 
  add_global_p()

Caractéristique	OR	95% IC	p-valeur
Sexe			<0,001
Femme	—	—
Homme	1,55	1,26 – 1,91
Groupe d'âges			<0,001
18-24 ans	—	—
25-44 ans	0,66	0,42 – 1,03
45-64 ans	0,34	0,21 – 0,54
65 ans et plus	0,25	0,15 – 0,43
Niveau d'études			<0,001
Primaire	—	—
Secondaire	2,59	1,77 – 3,83
Technique / Professionnel	2,86	1,98 – 4,17
Supérieur	6,63	4,55 – 9,80
Non documenté	8,59	4,53 – 16,6
Rapport à la religion			0,5
Pratiquant regulier	—	—
Pratiquant occasionnel	0,98	0,68 – 1,42
Appartenance sans pratique	0,99	0,71 – 1,40
Ni croyance ni appartenance	0,81	0,55 – 1,18
Rejet	0,68	0,39 – 1,19
NSP ou NVPR	0,92	0,40 – 2,02
Heures de télévision / jour	0,89	0,83 – 0,95	<0,001
Abréviations: IC = intervalle de confiance, OR = rapport de cotes

Table 22.7: Ajout des p-valeurs globales

Note

Concernant le test réalisé dans le cadre d’une Anova, il existe trois tests différents que l’on présente comme le type 1, le type 2 et le type 3 (ou I, II et III). Pour une explication sur ces différents types, on pourra se référer (en anglais) à https://mcfromnz.wordpress.com/2011/03/02/anova-type-iiiiii-ss-explained/ ou encore http://md.psych.bio.uni-goettingen.de/mv/unit/lm_cat/lm_cat_unbal_ss_explained.html.

Le type I n’est pas recommandé dans le cas présent car il dépend de l’ordre dans lequel les différentes variables sont testées.

Lorsqu’il n’y a pas d’interaction dans un modèle, le type II serait à privilégier car plus puissant (nous aborderons les interactions dans un prochain chapitre, cf. Chapitre 26).

En présence d’interactions, il est conseillé d’avoir plutôt recours au type III. Cependant, en toute rigueur, pour utiliser le type III, il faut que les variables catégorielles soient codées en utilisant un contrastes dont la somme est nulle (un contraste de type somme ou polynomial). Or, par défaut, les variables catégorielles sont codées avec un contraste de type traitement (nous aborderons les différents types de contrastes plus tard, cf. Chapitre 25).

Par défaut, car::Anova() utilise le type II et gtsummary::add_global_p() le type III. Dans les deux cas, il est possible de préciser le type de test avec type = "II" ou type = "III".

Dans le cas de notre exemple, un modèle simple sans interaction, le type de test ne change pas les résultats.

22.9 Régressions logistiques univariables

Les usages varient selon les disciplines et les revues scientifiques, mais il n’est pas rare de présenter, avant le modèle logistique multivariable, une succession de modèles logistiques univariables (i.e. avec une seule variable explicative à la fois) afin de présenter les odds ratios et leur intervalle de confiance et p-valeur associés avant l’ajustement multiniveau.

Afin d’éviter le code fastidieux consistant à réaliser chaque modèle un par un (par exemple glm(sport ~ sexe, family = binomial, data = d)) puis à en fusionner les résultats, on pourra tirer partie de gtsummary::tbl_uvregression() qui permet de réaliser toutes ces régressions individuelles en une fois et de les présenter dans un tableau synthétique.

d |>
  tbl_uvregression(
    y = sport,
    include = c(sexe, groupe_ages, etudes, relig, heures.tv),
    method = glm,
    method.args = list(family = binomial),
    exponentiate = TRUE
  ) |> 
  bold_labels()

Caractéristique	N	OR	95% IC	p-valeur
Sexe	2 000
Femme		—	—
Homme		1,47	1,22 – 1,77	<0,001
Groupe d'âges	2 000
18-24 ans		—	—
25-44 ans		0,51	0,35 – 0,71	<0,001
45-64 ans		0,20	0,14 – 0,28	<0,001
65 ans et plus		0,10	0,07 – 0,15	<0,001
Niveau d'études	2 000
Primaire		—	—
Secondaire		3,61	2,52 – 5,23	<0,001
Technique / Professionnel		4,75	3,42 – 6,72	<0,001
Supérieur		11,4	8,11 – 16,3	<0,001
Non documenté		26,2	15,7 – 44,9	<0,001
Rapport à la religion	2 000
Pratiquant regulier		—	—
Pratiquant occasionnel		1,08	0,78 – 1,50	0,6
Appartenance sans pratique		1,31	0,98 – 1,78	0,071
Ni croyance ni appartenance		1,45	1,05 – 2,02	0,026
Rejet		1,19	0,72 – 1,95	0,5
NSP ou NVPR		0,93	0,44 – 1,88	0,8
Heures de télévision / jour	1 995	0,79	0,74 – 0,84	<0,001
Abréviations: IC = intervalle de confiance, OR = rapport de cotes

Table 22.8: Régressions logistiques univariables

22.10 Présenter l’ensemble des résultats dans un même tableau

La fonction gtsummary::tbl_merge() permet de fusionner plusieurs tableaux (en tenant compte du nom des variables) et donc de présenter les différents résultats de l’analyse descriptive, univariable et multivariable dans un seul et même tableau.

tbl_desc <-
  d |> 
  tbl_summary(
    by = sport,
    include = c(sexe, groupe_ages, etudes, relig, heures.tv),
    statistic = all_categorical() ~ "{p}% ({n}/{N})",
    percent = "row",
    digits = all_categorical() ~ c(1, 0, 0)
  ) |> 
  modify_column_hide("stat_1") |> 
  modify_header("stat_2" ~ "**Pratique d'un sport**")

tbl_uni <-
  d |>
  tbl_uvregression(
    y = sport,
    include = c(sexe, groupe_ages, etudes, relig, heures.tv),
    method = glm,
    method.args = list(family = binomial),
    exponentiate = TRUE
  ) |> 
  modify_column_hide("stat_n")

tbl_multi <-
  mod |> 
  tbl_regression(exponentiate = TRUE)

list(tbl_desc, tbl_uni, tbl_multi) |> 
  tbl_merge(
    tab_spanner = c(
      NA,
      "**Régressions univariables**",
      "**Régression multivariable**"
    )
  ) |> 
  bold_labels()

Caractéristique	Pratique d’un sport¹	Régressions univariables			Régression multivariable
Caractéristique	Pratique d’un sport¹	OR	95% IC	p-valeur	OR	95% IC	p-valeur
Sexe
Femme	32,2% (354/1 101)	—	—		—	—
Homme	41,0% (369/899)	1,47	1,22 – 1,77	<0,001	1,55	1,26 – 1,91	<0,001
Groupe d'âges
18-24 ans	65,7% (111/169)	—	—		—	—
25-44 ans	49,2% (347/706)	0,51	0,35 – 0,71	<0,001	0,66	0,42 – 1,03	0,065
45-64 ans	27,4% (204/745)	0,20	0,14 – 0,28	<0,001	0,34	0,21 – 0,54	<0,001
65 ans et plus	16,1% (61/380)	0,10	0,07 – 0,15	<0,001	0,25	0,15 – 0,43	<0,001
Niveau d'études
Primaire	10,7% (50/466)	—	—		—	—
Secondaire	30,2% (117/387)	3,61	2,52 – 5,23	<0,001	2,59	1,77 – 3,83	<0,001
Technique / Professionnel	36,4% (216/594)	4,75	3,42 – 6,72	<0,001	2,86	1,98 – 4,17	<0,001
Supérieur	57,8% (255/441)	11,4	8,11 – 16,3	<0,001	6,63	4,55 – 9,80	<0,001
Non documenté	75,9% (85/112)	26,2	15,7 – 44,9	<0,001	8,59	4,53 – 16,6	<0,001
Rapport à la religion
Pratiquant regulier	31,6% (84/266)	—	—		—	—
Pratiquant occasionnel	33,3% (147/442)	1,08	0,78 – 1,50	0,6	0,98	0,68 – 1,42	>0,9
Appartenance sans pratique	37,8% (287/760)	1,31	0,98 – 1,78	0,071	0,99	0,71 – 1,40	>0,9
Ni croyance ni appartenance	40,1% (160/399)	1,45	1,05 – 2,02	0,026	0,81	0,55 – 1,18	0,3
Rejet	35,5% (33/93)	1,19	0,72 – 1,95	0,5	0,68	0,39 – 1,19	0,2
NSP ou NVPR	30,0% (12/40)	0,93	0,44 – 1,88	0,8	0,92	0,40 – 2,02	0,8
Heures de télévision / jour	2,00 (1,00 – 3,00)	0,79	0,74 – 0,84	<0,001	0,89	0,83 – 0,95	<0,001
Manquant	3
Abréviations: IC = intervalle de confiance, OR = rapport de cotes
¹ % (n/N); Médiane (Q1 – Q3)

Table 22.9: tableau synthétique de l’analyse

Le diaporama ci-dessous vous permet de visualiser chaque étape du code correspondant au graphique précédent.

22.11 webin-R

La régression logistique est présentée sur YouTube dans le webin-R #06 (régression logistique (partie 1)) et le le webin-R #07 (régression logistique (partie 2)).