library(tidyverse)
library(labelled)
data(hdv2003, package = "questionr")
d <-
hdv2003 |>
mutate(
sexe = sexe |> fct_relevel("Femme"),
groupe_ages = age |>
cut(
c(18, 25, 45, 65, 99),
right = FALSE,
include.lowest = TRUE,
labels = c("18-24 ans", "25-44 ans",
"45-64 ans", "65 ans et plus")
),
etudes = nivetud |>
fct_recode(
"Primaire" = "N'a jamais fait d'etudes",
"Primaire" = "A arrete ses etudes, avant la derniere annee d'etudes primaires",
"Primaire" = "Derniere annee d'etudes primaires",
"Secondaire" = "1er cycle",
"Secondaire" = "2eme cycle",
"Technique / Professionnel" = "Enseignement technique ou professionnel court",
"Technique / Professionnel" = "Enseignement technique ou professionnel long",
"Supérieur" = "Enseignement superieur y compris technique superieur"
) |>
fct_na_value_to_level("Non documenté")
) |>
set_variable_labels(
sport = "Pratique un sport ?",
sexe = "Sexe",
groupe_ages = "Groupe d'âges",
etudes = "Niveau d'études",
relig = "Rapport à la religion",
heures.tv = "Heures de télévision / jour",
poids = "Pondération de l'enquête"
)32 Régression logistique binaire pondérée
Nous avons abordé la régression logistique binaire non pondérée dans un chapitre dédié, cf. Chapitre 22. Elle se réalise classiquement avec la fonction glm() en spécifiant family = binomial.
Lorsque l’on utilise des données d’enquêtes, l’approche est similaire sauf que l’on aura recours à la fonction survey::svyglm() qui sait gérer des objets survey : non seulement la pondération sera prise en compte, mais le calcul des intervalles de confiance et des p-valeurs sera ajusté en fonction du plan d’échantillonnage.
32.1 Données des exemples
Nous allons reprendre les même données issues de l’enquête Histoire de vie 2003, mais en tenant compte cette fois-ci des poids de pondération fourni dans la variable poids.
Il ne nous reste qu’à définir notre objet survey en spécifiant la pondération fournie avec l’enquête. La documentation ne mentionne ni strates ni grappes.
32.2 Calcul de la régression logistique binaire
La syntaxe de survey::svyglm() est similaire à celle de glm() sauf qu’elle a un argument design au lieu de data.
La plupart du temps, les poids de pondération ne sont pas des nombres entiers, mais des nombres décimaux. Or, la famille de modèles binomiaux repose sur des nombres entiers de succès et d’échecs. Avec une version récente1 de R, cela n’est pas problématique. Nous aurons simplement un avertissement.
1 Si vous utilisez une version ancienne de R, cela n’était tout simplement pas possible. Vous obteniez un message d’erreur et le modèle n’était pas calculé. Si c’est votre cas, optez pour un modèle quasi-binomial ou bien mettez à jour R.
mod_binomial <- svyglm(
sport ~ sexe + groupe_ages + etudes + relig + heures.tv,
family = binomial,
design = dp
)Warning in eval(family$initialize): nombre de succès non entier dans un glm
binomial !Une alternative consiste à avoir recours à la famille quasi-binomiale, que l’on spécifie avec family = quasibinomial et qui constitue une extension de la famille binomiale pouvant gérer des poids non entiers. La distribution quasi-binomiale, bien que similaire à la distribution binomiale, possède un paramètre supplémentaire 𝜙 qui tente de décrire une variance supplémentaire dans les données qui ne peut être expliquée par une distribution binomiale seule (on parle alors de surdispersion). Les coefficients obtenus sont les mêmes, mais les intervalles de confiance peuvent être un peu plus large.
Simple, non ?
32.3 Sélection de modèle
Comme précédemment (cf. Chapitre 23), il est possible de procéder à une sélection de modèle pas à pas, par minimisation de l’AIC, avec step().
Start: AIC=2309.89
sport ~ sexe + groupe_ages + etudes + relig + heures.tv
Df Deviance AIC
- relig 5 2266.3 2302.2
<none> 2263.9 2309.9
- heures.tv 1 2276.2 2320.2
- sexe 1 2276.4 2320.4
- groupe_ages 3 2313.9 2353.8
- etudes 4 2383.5 2421.2
Step: AIC=2296.28
sport ~ sexe + groupe_ages + etudes + heures.tv
Df Deviance AIC
<none> 2266.3 2296.3
- heures.tv 1 2278.4 2306.4
- sexe 1 2279.0 2307.0
- groupe_ages 3 2318.3 2342.1
- etudes 4 2387.2 2408.8
Sélection pas à pas et valeurs manquantes
Nous avons abordé dans le chapitre sur la sélection de modèle pas à pas la problématique des valeurs manquantes lors d’une sélection pas à pas descendante par minimisation de l’AIC (cf. Section 23.8). La même approche peut être appliquée avec des données pondérées, à l’aide de la fonction guideR::step_with_na(), compatible avec les modèles survey::svyglm(). Il faudra néanmoins, dans ce cas là, qu’on lui passe l’objet survey ayant servi au calcul du modèle via l’e paramètre’argument design.
32.4 Affichage des résultats
Nous pouvons tout à fait utiliser gtsumarry::tbl_regression() avec ce type de modèles. De même, on peut utiliser gtsummary::add_global_p() pour calculer les p-valeurs globales des variables ou encore gtsummary::add_vif() pour vérifier la multicolinéarité (cf. Chapitre 27).
mod_quasi2 |>
tbl_regression(exponentiate = TRUE) |>
add_global_p(keep = TRUE) |>
add_vif() |>
bold_labels()| Caractéristique | OR1 | 95% IC1 | p-valeur | GVIF1 | Adjusted GVIF2,1 |
|---|---|---|---|---|---|
| Sexe | 0,005 | 1,0 | 1,0 | ||
| Femme | — | — | |||
| Homme | 1,44 | 1,12 – 1,87 | 0,005 | ||
| Groupe d'âges | <0,001 | 2,1 | 1,1 | ||
| 18-24 ans | — | — | |||
| 25-44 ans | 0,85 | 0,48 – 1,51 | 0,6 | ||
| 45-64 ans | 0,40 | 0,22 – 0,73 | 0,003 | ||
| 65 ans et plus | 0,37 | 0,19 – 0,72 | 0,004 | ||
| Niveau d'études | <0,001 | 2,2 | 1,1 | ||
| Primaire | — | — | |||
| Secondaire | 2,66 | 1,62 – 4,38 | <0,001 | ||
| Technique / Professionnel | 3,09 | 1,90 – 5,00 | <0,001 | ||
| Supérieur | 6,54 | 3,99 – 10,7 | <0,001 | ||
| Non documenté | 10,3 | 4,60 – 23,0 | <0,001 | ||
| Heures de télévision / jour | 0,89 | 0,82 – 0,97 | 0,006 | 1,1 | 1,0 |
| 1 OR = rapport de cotes, IC = intervalle de confiance, GVIF = Generalized Variance Inflation Factor | |||||
| 2 GVIF2 | |||||
2 1/(2*df)
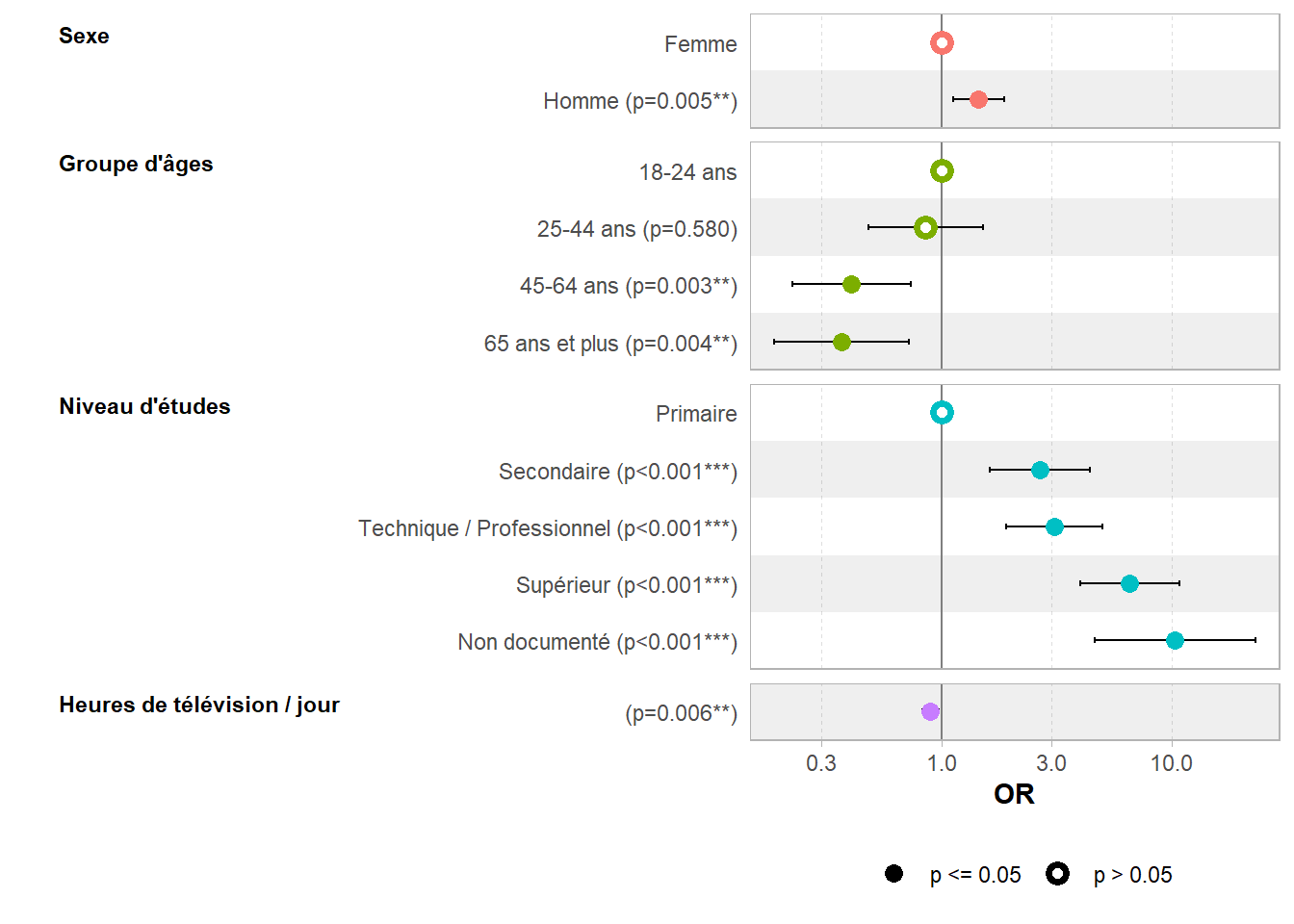
Pour un graphique des coefficients, nous pouvons utiliser ggstats::ggcoef_model().
32.5 Prédictions marginales
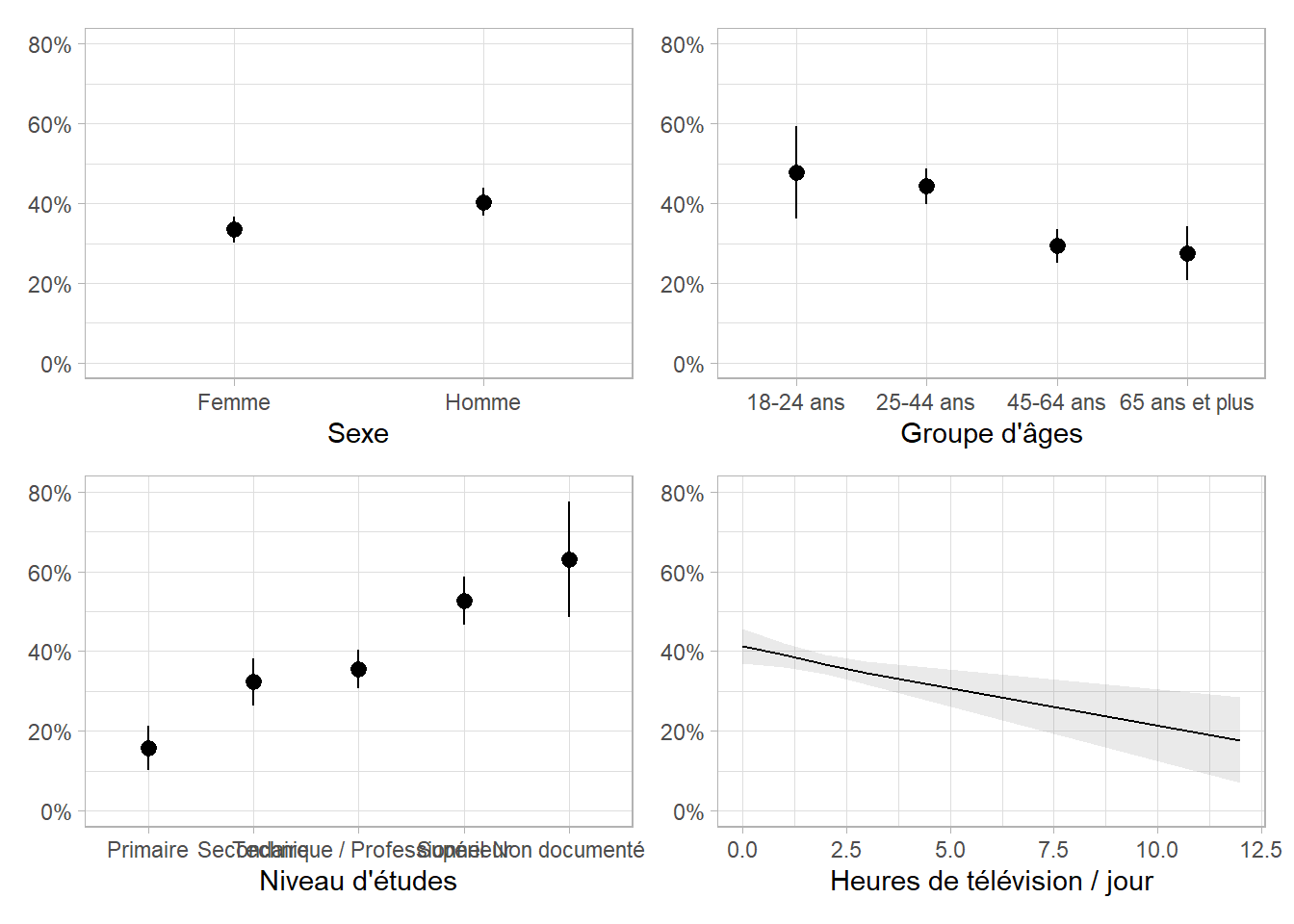
Pour visualiser les prédictions marginales moyennes du modèle (cf. Section 24.3), nous pouvons utiliser broom.helpers::plot_marginal_predictions().
mod_quasi2 |>
broom.helpers::plot_marginal_predictions(type = "response") |>
patchwork::wrap_plots() &
scale_y_continuous(
limits = c(0, .8),
labels = scales::label_percent()
)Warning: With models of this class, it is normally good practice to specify
weights using the `wts` argument. Otherwise, weights will be ignored in the
computation of quantities of interest.
Warning: With models of this class, it is normally good practice to specify
weights using the `wts` argument. Otherwise, weights will be ignored in the
computation of quantities of interest.
Warning: With models of this class, it is normally good practice to specify
weights using the `wts` argument. Otherwise, weights will be ignored in the
computation of quantities of interest.
Warning: With models of this class, it is normally good practice to specify
weights using the `wts` argument. Otherwise, weights will be ignored in the
computation of quantities of interest.