library(labelled)
library(tidyverse)
load(url("https://github.com/larmarange/guide-R/raw/main/analyses_avancees/ressources/DebTrivedi.rda"))
d <- DebTrivedi |>
mutate(
gender = gender |>
fct_recode("femme" = "female", "homme" = "male"),
privins = privins |>
fct_recode("non" = "no", "oui" = "yes"),
health = health |>
fct_recode(
"pauvre" = "poor",
"moyenne" = "average",
"excellente" = "excellent"
)
) |>
set_variable_labels(
ofp = "Nombre de visites médicales",
gender = "Genre de l'assuré",
privins = "Dispose d'une assurance privée ?",
health = "Santé perçue",
numchron = "Nombre de conditions chroniques"
)
contrasts(d$health) <- contr.treatment(3, base = 2)47 Modèles de comptage zero-inflated et hurdle
Dans certaines situations, les modèles de comptage (cf. Chapitre 45) ont des difficultés à estimer correctement le nombre d’individus n’ayant pas vécu l’évènement (i.e. le nombre de 0).
47.1 Données d’illustration
Dans ce chapitre, nous allons utiliser un jeu de données issu d’un article de Partha Deb et Pravin K. Trivedi (Deb et Trivedi 1997). Ce jeu de données porte sur 4406 individus âgés de 66 ans ou plus et couvert par le programme américain Medicare.
Deb, Partha, et Pravin K. Trivedi. 1997. « Demand for Medical Care by the Elderly: A Finite Mixture Approach ». Journal of Applied Econometrics 12 (3): 313‑36. https://doi.org/10.1002/(SICI)1099-1255(199705)12:3<313::AID-JAE440>3.0.CO;2-G.
L’analyse va porter sur la demande de soins, mesurée ici à travers le nombre de visites médicales (ofp). Pour les variables explicatives, nous allons considérer le genre du patient (gender), le fait de disposer d’une assurance privée (privins), la santé perçue (health) et le nombre de conditions chroniques de l’assuré.
Chargeons et préparons rapidement les données. Nous allons recoder les variables catégorielles en français (Section 9.3) et ajouter des étiquettes de variables (cf. Chapitre 11).
47.2 Modèles de comptage classique
Commençons tout d’abord par une approche classique (Chapitre 45) : calculons un modèle de Poisson et vérifions la surdispersion.
mod_poisson <- glm(
ofp ~ gender + privins + health + numchron,
family = poisson,
data = d
)
mod_poisson |>
performance::check_overdispersion()# Overdispersion test
dispersion ratio = 7.103
Pearson's Chi-Squared = 31254.867
p-value = < 0.001Overdispersion detected.Une surdispersion étant détectée, basculons sur un modèle négatif binomial.
mod_nb <- MASS::glm.nb(
ofp ~ gender + privins + health + numchron,
data = d
)
mod_nb |>
performance::check_overdispersion()# Overdispersion test
dispersion ratio = 1.050
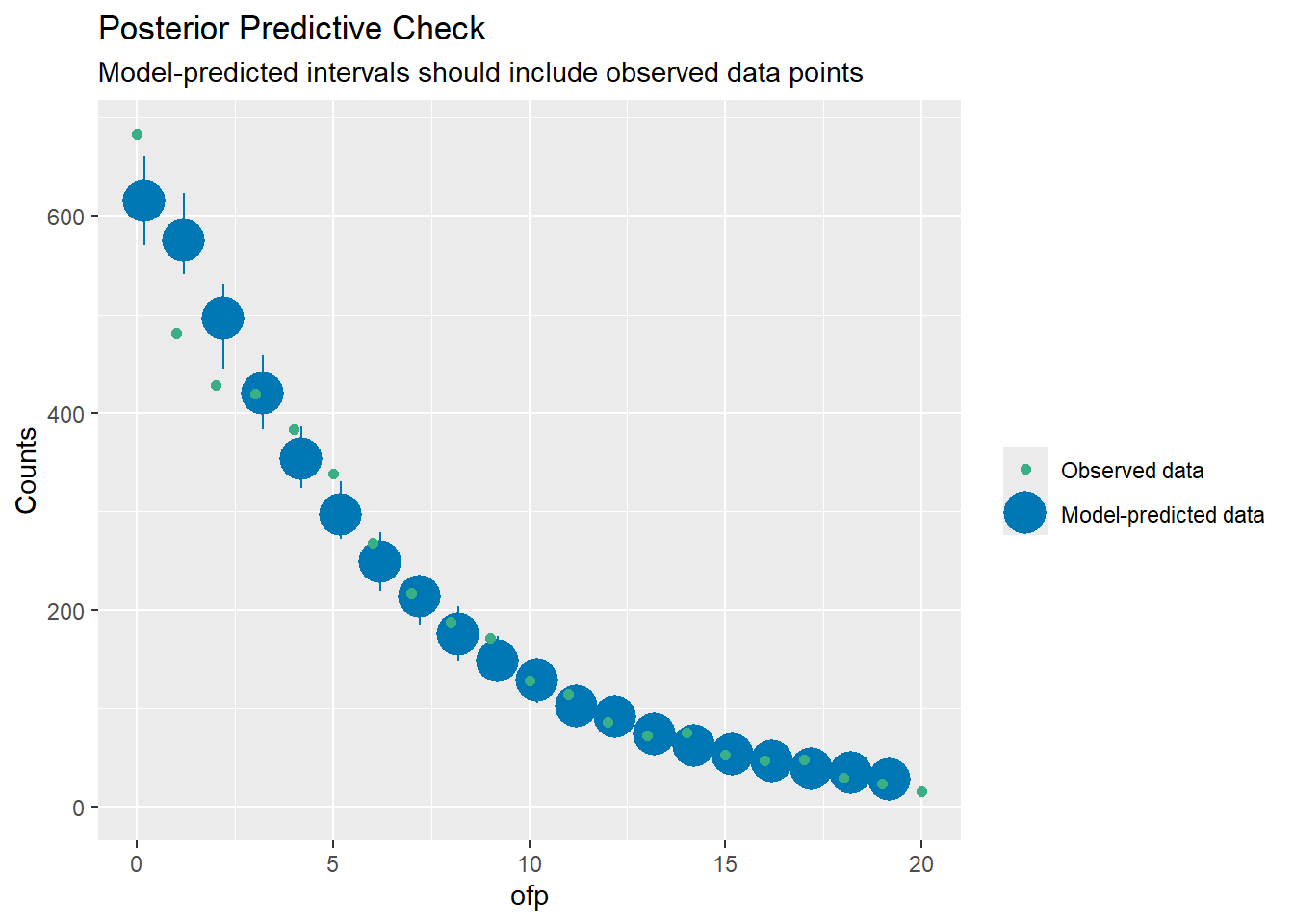
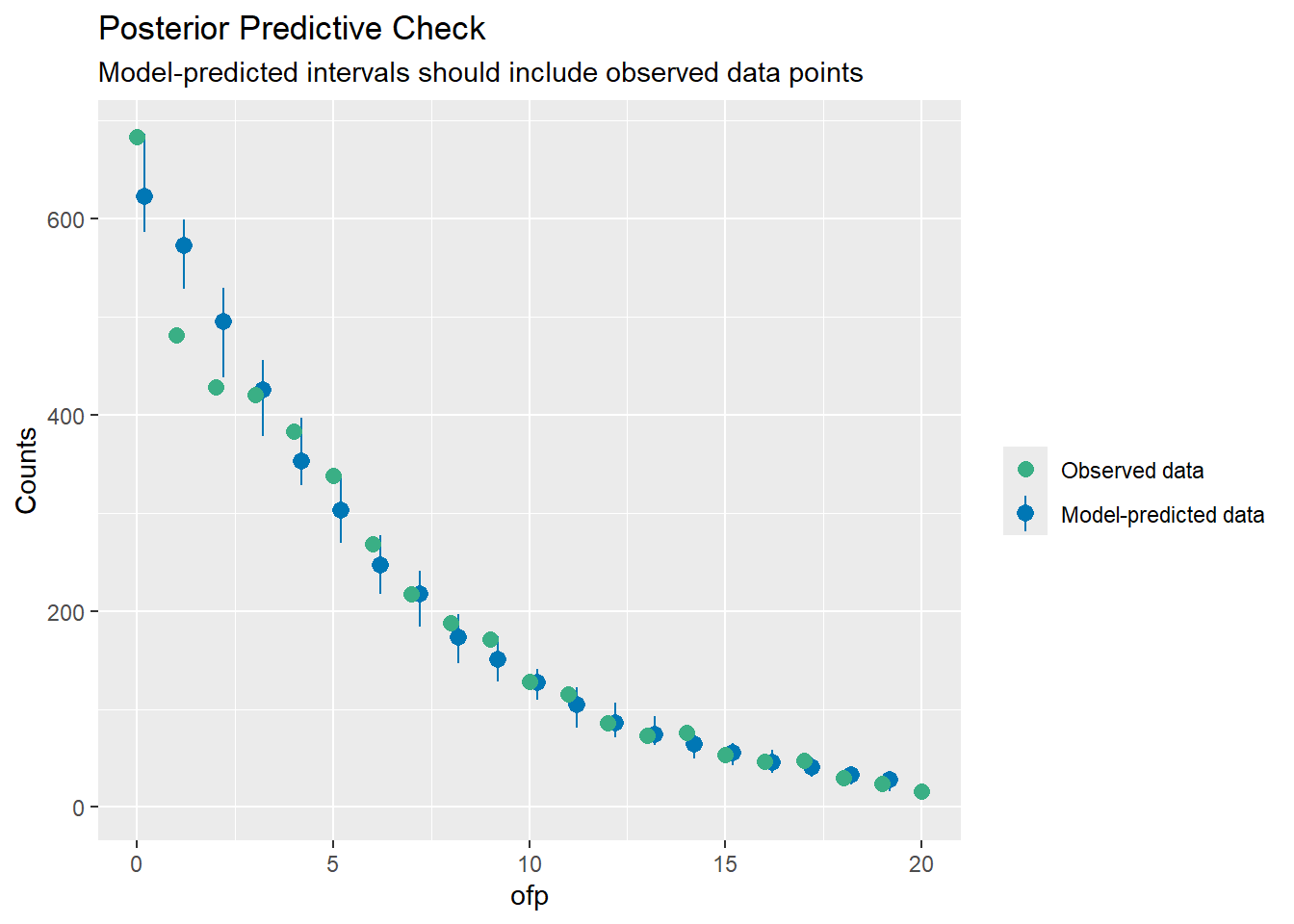
p-value = 0.36No overdispersion detected.Le modèle négatif binomial ne règle pas notre problème de surdispersion. Comparons les valeurs observées avec les valeurs théoriques avec performance::check_predictions()1. Pour faciliter la lecture du graphique, nous allons zoomer
sur les 20 premières valeurs.
1 Nous aurions aussi pu utiliser la fonction observed_vs_theoretical() présentée dans le chapitre sur les modèles de comptage (cf. Section 45.1.4).
Comme nous pouvons le voir sur ce graphique, le nombre de 0 prédit par le modèle est inférieur à celui observé. Cela signifie que les 0 sont sur-représentés dans nos données par rapport à une distribution négative binomiale. Ces 0 ont tendance à tirer
la moyenne vers le bas. Dès lors, le nombre de 1 et de 2 prédits par le modèle sont quant à eux sur-représentés par rapport aux données observées. On dit alors qu’il y a une inflation de zéros
dans les données (zero-inflated en anglais).
On peut essayer de regarder s’il y a une sous- ou une sur-représentation de zéros avec la fonction performance::check_zeroinflation().
47.3 Modèles zero-inflated
Les modèles zero-inflated ont justement été prévus pour ce cas de figure. Un modèle de Poisson zero-inflated combine deux modèles : un modèle logistique binaire et un modèle de Poisson. Dans un premier temps, on applique le modèle logistique binaire. Si la valeur obtenue est 0, le résultat final est 0. Si la valeur obtenue est 1, alors on applique le modèle de Poisson.
Les modèles de Poisson zero-inflated sont notamment implémentés dans le package pscl via la fonction pscl::zeroinfl().
Calculons un premier modèle de Poisson zero-inflated.
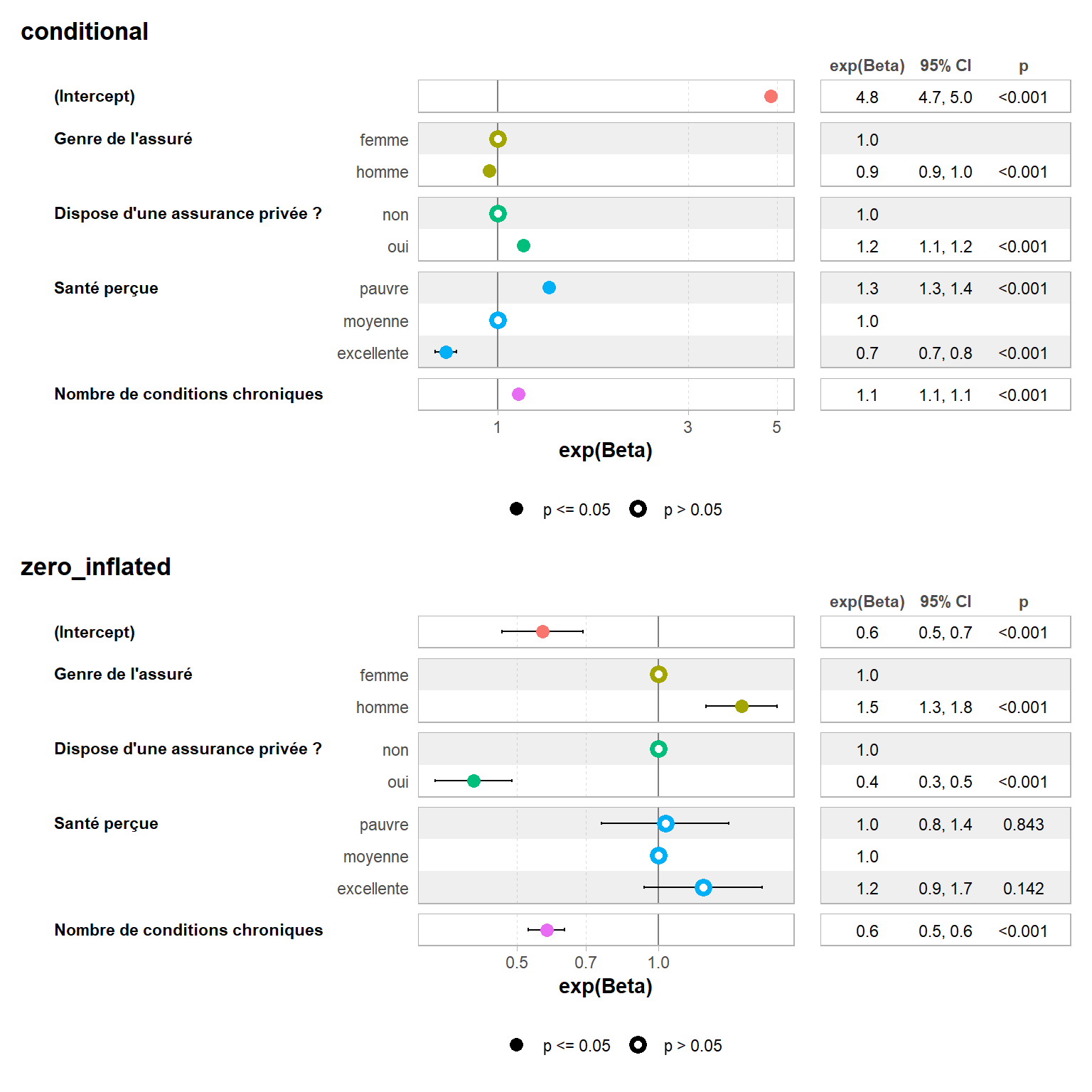
Regardons les coefficients du modèle (en forçant l’affichage des intercepts). Comme il s’agit d’un modèle à plusieurs composantes, nous aurons recours à ggstats::ggcoef_multicomponents().
ℹ <zeroinfl> model detected.✔ `tidy_zeroinfl()` used instead.ℹ Add `tidy_fun = broom.helpers::tidy_zeroinfl` to quiet these messages.
Nous obtenons deux séries de coefficients : une série conditional correspondant au modèle de Poisson et une série zero_inflated correspondant au modèle logistique binaire. Nous avons représenter les exponentiels des coefficients, qui s’interprètent donc comme des risk ratio pour le modèle de Poisson et des odds ratio pour le modèle logistique.
Les variables ayant un effet significatif ne sont pas les mêmes pour les deux composantes du modèle. Il est d’ailleurs possible d’utiliser des variables différentes pour chaque composante, en écrivant d’abord l’équation du modèle de Poisson, puis celle du modèle logistique et en les séparant avec le symbole |. D’ailleurs, la syntaxe ofp ~ gender + privins + health + numchron est équivalente à ofp ~ gender + privins + health + numchron | gender + privins + health + numchron. Dans la littérature, on trouve fréquemment des modèles de Poisson zero-inflated simplifiés où seul un intercept est utilisé pour la composante logistique binaire.
mod_zip_simple |>
ggstats::ggcoef_multicomponents(
type = "table",
tidy_fun = broom.helpers::tidy_zeroinfl,
exponentiate = TRUE,
intercept = TRUE,
component_label = c(
conditional = "Modèle de Poisson",
zero_inflated = "Modèle logistique binaire"
)
) +
patchwork::plot_layout(heights = c(6, 1))
Pour ce jeu de données, cela ne modifie que peu les coefficients de la composante modèle de comptage.
De même, il est possible de préférer un modèle négatif binomial plutôt que Poisson pour la composante modèle de comptage. Il suffit d’ajouter l’argument dist = "negbin".
Nous pouvons aisément comparer l’AIC de ces différents modèles.
performance::compare_performance(
mod_poisson,
mod_zip_simple,
mod_zip,
mod_nb,
mod_zinb,
metrics = "AIC"
)# Comparison of Model Performance Indices
Name | Model | AIC (weights)
-------------------------------------------
mod_poisson | glm | 36792.1 (<.001)
mod_zip_simple | zeroinfl | 33308.5 (<.001)
mod_zip | zeroinfl | 33014.2 (<.001)
mod_nb | negbin | 24505.7 (<.001)
mod_zinb | zeroinfl | 24380.9 (>.999)Comparons les coefficients de la composante comptage
du modèle négatif binomial zero-inflated avec ceux du modèle négatif binomial classique.
library(gtsummary)
tbl_nb <- mod_nb |>
tbl_regression(exponentiate = TRUE)
tbl_zinb <- mod_zinb |>
tbl_regression(
tidy_fun = broom.helpers::tidy_zeroinfl,
component = "conditional",
exponentiate = TRUE
)
list(tbl_nb, tbl_zinb) |>
tbl_merge(c("**NB**", "**ZI-NB**")) |>
bold_labels()Characteristic |
NB |
ZI-NB |
||||
|---|---|---|---|---|---|---|
|
IRR 1 |
95% CI 1 |
p-value |
exp(Beta) |
95% CI 1 |
p-value |
|
| Genre de l'assuré | ||||||
| femme | — | — | — | — | ||
| homme | 0.90 | 0.84, 0.95 | <0.001 | 0.93 | 0.88, 0.99 | 0.031 |
| Dispose d'une assurance privée ? | ||||||
| non | — | — | — | — | ||
| oui | 1.39 | 1.29, 1.50 | <0.001 | 1.23 | 1.14, 1.33 | <0.001 |
| Santé perçue | ||||||
| pauvre | 1.39 | 1.27, 1.53 | <0.001 | 1.38 | 1.26, 1.51 | <0.001 |
| moyenne | — | — | — | — | ||
| excellente | 0.71 | 0.63, 0.80 | <0.001 | 0.71 | 0.63, 0.81 | <0.001 |
| Nombre de conditions chroniques | 1.21 | 1.19, 1.25 | <0.001 | 1.16 | 1.13, 1.19 | <0.001 |
|
1
IRR = Incidence Rate Ratio, CI = Confidence Interval |
||||||
Comme nous pouvons le voir, les résultats sont relativement proches.
Si l’interprétation du modèle de comptage reste classique, celle du modèle logistique binaire est parfois un peu plus complexe. En effet, il y a deux sources de 0 dans le modèle zero-inflated : si certains sont générés par la composante logistique binaire (dont c’est justement le rôle), le modèle de comptage génère lui aussi des 0. Dès lors, le modèle logistique binaire ne suffit pas à lui seul à identifier les facteurs associés de vivre au moins une fois l’évènement.
Si l’objectif de l’analyse est avant tout d’identifier les facteurs associés avec le nombre moyen d’évènements, on pourra éventuellement se contenter d’un modèle zero-inflated simple, c’est-à-dire avec seulement un intercept pour la composante zero-inflated afin de corriger la sur-représentation des zéros dans nos données.
Alternativement, on pourra se tourner vers un modèle avec saut
qui distingue les valeurs nulles des valeurs positives : les modèles hurdle en anglais.
47.4 Modèles hurdle
Les modèles hurdle se distinguent des modèles zero-inflated dans le sens où l’on combine un modèle logistique binomial pour déterminer si les individus ont vécu au moins une fois l’évènement et un modèle de comptage tronqué
(qui n’accepte que des valeurs strictement positives) qui détermine le nombre d’évènements vécus uniquement pour ceux l’ayant vécu au moins une fois.
Les modèles zero-inflated et hurdle diffèrent par leur conceptualisation des zéros et l’interprétation des paramètres du modèle (C. X. Feng 2021).
Feng, Cindy Xin. 2021. « A comparison of zero-inflated and hurdle models for modeling zero-inflated count data ». Journal of Statistical Distributions and Applications 8 (1): 8. https://doi.org/10.1186/s40488-021-00121-4.
Un modèle zero-inflated suppose que les comptes nuls résultent d’un mélange de deux distributions, l’une où les sujets produisent toujours des comptes nuls, souvent appelés “zéros structurels” ou “zéros excessifs”. Les sujets qui sont exposés au résultat mais qui n’ont pas ou n’ont pas rapporté l’expérience du résultat au cours de la période d’étude sont appelés “zéros d’échantillonnage”. La différenciation des zéros en deux groupes se justifie par le fait que les zéros excessifs sont souvent dus à l’existence d’une sous-population de sujets qui ne sont pas exposés à certains résultats au cours de la période d’étude. Par exemple, lors de la modélisation du nombre de comportements à haut risque, certains participants peuvent obtenir un score de zéro parce qu’ils ne sont pas exposés à un tel comportement à risque pour la santé ; il s’agit des zéros structurels puisqu’ils ne peuvent pas présenter de tels comportements à haut risque. D’autres participants à risque peuvent obtenir un score de zéro parce qu’ils n’ont pas manifesté de tels comportements à risque au cours de la période étudiée. La probabilité d’appartenir à l’une ou l’autre population est estimée à l’aide d’une composante de probabilité à inflation nulle, tandis que les effectifs de la seconde population du groupe d’utilisateurs sont modélisés par une distribution de comptage ordinaire, telle qu’une distribution de Poisson ou binomiale négative.
En revanche, un modèle hurdle suppose que toutes les données nulles proviennent d’une source “structurelle”, une partie du modèle étant un modèle binaire pour modéliser si la variable de réponse est nulle ou positive, et une autre partie utilisant un modèle tronqué, pour les données positives. Par exemple, dans les études sur l’utilisation des soins de santé, la partie zéro implique la décision de rechercher des soins, et la composante positive détermine la fréquence de l’utilisation au sein du groupe de l’utilisateur.
Une autre différence importante entre les modèles hurdle et zero-inflated est leur capacité à gérer la déflation zéro (moins de zéros que prévu par le processus de génération des données). Les modèles zero-inflated ne sont pas en mesure de gérer la déflation zéro, quel que soit le niveau d’un facteur, et donneront des estimations de paramètres de l’ordre de l’infini pour la composante logistique, alors que les modèles hurdle peuvent gérer la déflation zéro (Min et Agresti 2005).
Min, Yongyi, et Alan Agresti. 2005. « Random Effect Models for Repeated Measures of Zero-Inflated Count Data ». Statistical Modelling 5 (1): 1‑19. https://doi.org/10.1191/1471082X05st084oa.
Les modèles hurdle peuvent être calculés avec la fonction pscl::hurdle() dont la syntaxe est similaire à pscl::zeroinfl().
Regardons les coefficients obtenus.
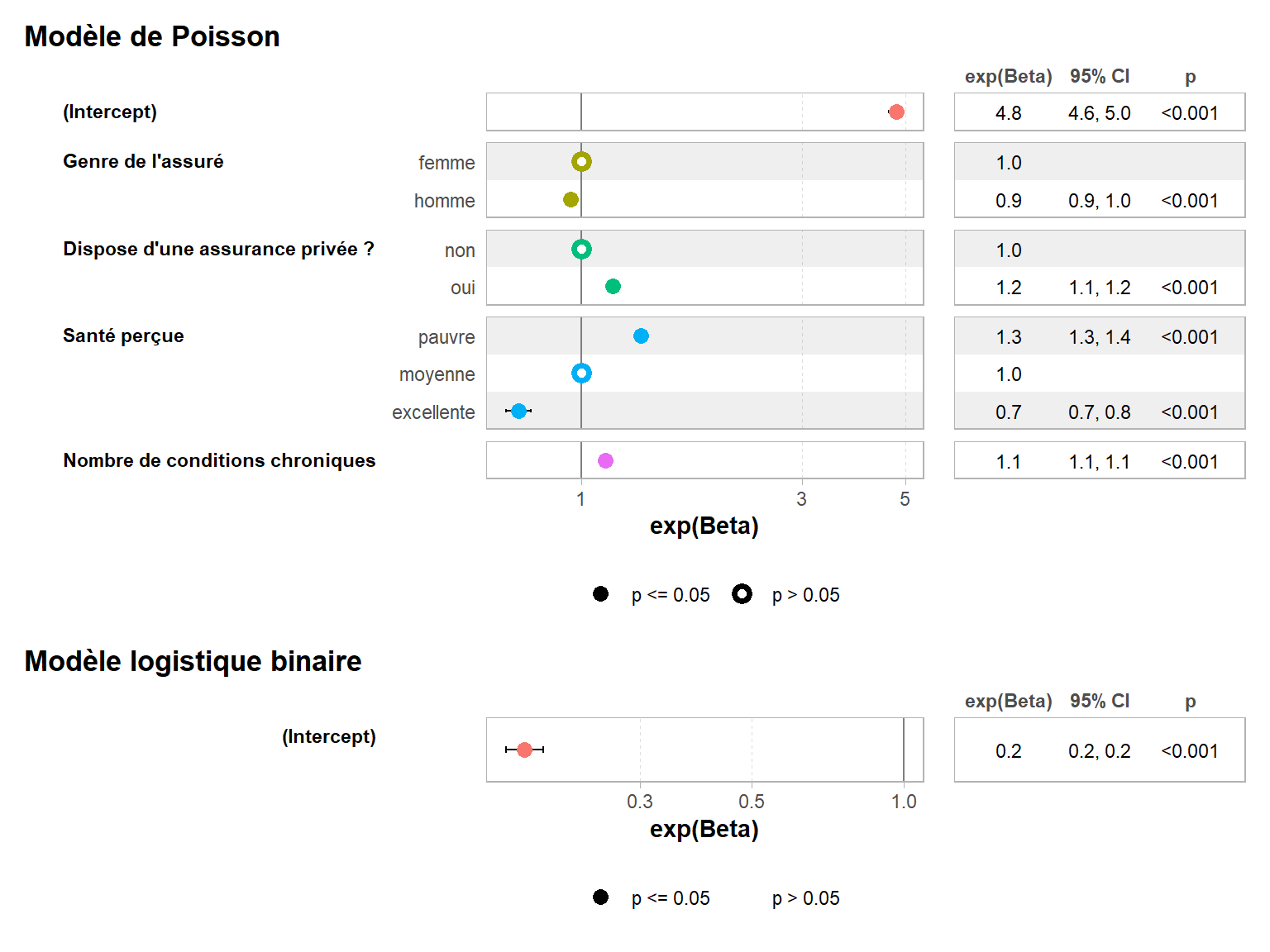
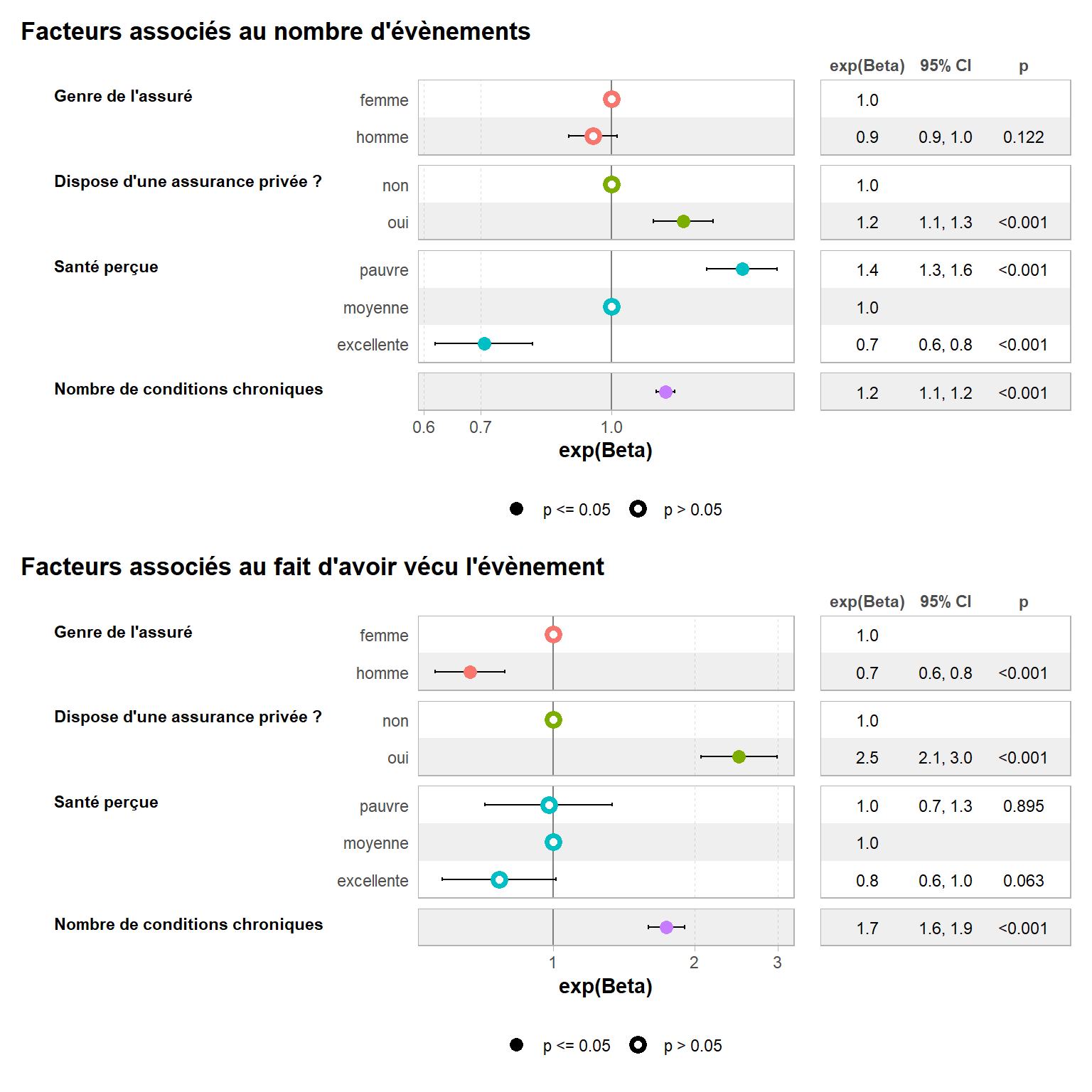
mod_hurdle_nb |>
ggstats::ggcoef_multicomponents(
type = "table",
tidy_fun = broom.helpers::tidy_zeroinfl,
exponentiate = TRUE,
component_label = c(
conditional = "Facteurs associés au nombre d'évènements",
zero_inflated = "Facteurs associés au fait d'avoir vécu l'évènement"
)
)
Nous pouvons également produire un tableau avec gtsummary::tbl_regression(). L’astuce consiste à générer un tableau pour chaque composante du modèle puis à les fusionner.
tbl_log <- mod_hurdle_nb |>
tbl_regression(
tidy_fun = broom.helpers::tidy_zeroinfl,
component = "zero_inflated",
exponentiate = TRUE
)
tbl_nb <- mod_hurdle_nb |>
tbl_regression(
tidy_fun = broom.helpers::tidy_zeroinfl,
component = "conditional",
exponentiate = TRUE
)
list(tbl_log, tbl_nb) |>
tbl_merge(
c(
"**OR (régression logistique)**",
"**RR (négatif binomial)**"
)
) |>
bold_labels()Characteristic |
OR (régression logistique) |
RR (négatif binomial) |
||||
|---|---|---|---|---|---|---|
exp(Beta) |
95% CI 1 |
p-value |
exp(Beta) |
95% CI 1 |
p-value |
|
| Genre de l'assuré | ||||||
| femme | — | — | — | — | ||
| homme | 0.67 | 0.56, 0.79 | <0.001 | 0.95 | 0.89, 1.01 | 0.12 |
| Dispose d'une assurance privée ? | ||||||
| non | — | — | — | — | ||
| oui | 2.48 | 2.06, 2.99 | <0.001 | 1.21 | 1.12, 1.32 | <0.001 |
| Santé perçue | ||||||
| pauvre | 0.98 | 0.72, 1.34 | 0.9 | 1.42 | 1.29, 1.57 | <0.001 |
| moyenne | — | — | — | — | ||
| excellente | 0.77 | 0.58, 1.01 | 0.063 | 0.71 | 0.62, 0.81 | <0.001 |
| Nombre de conditions chroniques | 1.74 | 1.59, 1.90 | <0.001 | 1.16 | 1.13, 1.19 | <0.001 |
|
1
CI = Confidence Interval |
||||||
Coefficients des deux composantes du modèle hurdle
Avec un tel modèle, on cherche à répondre à deux questions :
Quels sont les facteurs associés au fait d’avoir vécu l’évènement au moins une fois ?
Si l’on a vécu l’évènement au moins une fois, quels sont les facteurs associés à la fréquence de l’évènement ?
Dans notre exemple, le fait d’avoir une assurance privée joue à la fois sur le fait d’aller consulter un médecin et sur le nombre de consultations. Par contre, la santé perçue n’a pas d’effet sur le fait d’aller consulter mais, si l’on va consulter, cela va influer fortement sur le nombre de consultations. À l’inverse, le sexe de l’assuré a un effet sur le fait d’aller consulter (les hommes consultent moins que les femmes) mais, si l’on consulte, ne joue pas sur le nombre de consultations.
47.5 Modèles de taux zero-inflated ou hurdle
Il est tout à fait possible de réaliser un modèle de taux ou d’incidence (cf. Chapitre 46) zero-inflated ou hurdle. Pour cela, on rajoutera comme avec un modèle classique un décalage (offset) correspondant au logarithme de la durée d’exposition.
Ce décalage s’ajoute a minima à la composante comptage
du modèle zero-inflated ou du modèle hurdle. Toutefois, la probabilité de ne pas vivre l’évènement (donc de zéro) peut elle-même être influencée par la durée d’exposition, auquel cas il pourrait être pertinent d’ajouter également l’offset à la composante inflation des zéros
du modèle. Certains auteurs suggèrent même d’inclure le logarithme de la durée d’exposition non pas sous forme d’un offset mais directement comme une variable explicative du modèle (C. Feng 2022).
Feng, Cindy. 2022. « Zero-inflated models for adjusting varying exposures: a cautionary note on the pitfalls of using offset ». Journal of Applied Statistics 49 (1): 1‑23. https://doi.org/10.1080/02664763.2020.1796943.
47.6 Tuto@Mate
Les modèles de comptage zero-inflated sont présentés sur YouTube dans le Tuto@Mate#62.
47.7 Lectures complémentaires
Regression Models for Count Data in R par Achim Zeileis, Christian Kleiber et Simon Jackman
Too many zeros and/or highly skewed? A tutorial on modelling health behaviour as count data with Poisson and negative binomial regression par James A. Green. DOI : 10.1080/21642850.2021.1920416
A comparison of zero-inflated and hurdle models for modeling zero-inflated count data par Cindy Xin Feng. DOI : 10.1186/s40488-021-00121-4
Zero-inflated models for adjusting varying exposures: a cautionary note on the pitfalls of using offset by Cindy Xin Feng. DOI : 10.1080/02664763.2020.1796943