42 Analyse de survie

L’analyse de survie s’intéresse à la survenue d’un évènement au cours du temps. Elle tire son nom de l’analyse de la mortalité en démographie.

Elle nécessite d’identifier un évènement origine qui servira de point de départ de notre calendrier (par exemple la naissance), de définir une unité de temps (par exemple en années), et un évènement d’intérêt (par exemple le décès).

Dans l’analyse de survie simple que nous aborderons ici, cet évènement est binaire et unique, c’est-à-dire qu’il ne peut avoir lieu qu’une fois et que nous ne considérons que deux états : non vécu / vécu¹. Ainsi, l’analyse de survie simple n’est pas adaptée pour l’étude de la survenue d’un enfant car l’on peut avoir plusieurs enfants. Par contre, on peut étudier la survenue d’un premier enfant (évènement unique) depuis la mise en couple (évènement origine).

¹ Il existe des modèles de survie plus complexe dit multi-états dans lesquels il est possible de prendre en compte plusieurs types de transitions; où encore des modèles à évènements répétés.

² De même, il est possible de concevoir des modèles plus complexes avec prise en compte d’une censure à droite.

De même, nous allons supposer ici que tous les individus sont observés depuis l’évènement origine, autrement dit qu’il n’y a pas de censure à gauche². Par contre, nous allons considérer la possibilité d’une censure à droite, c’est-à-dire que tous les individus ne seront peut être pas observé jusqu’à la survenue de l’évènement et que certains pourront ne jamais le vivre. Par exemple, si dans notre enquête nous avons un couple ensemble depuis 3 ans et sans enfant au moment de l’enquête, nous savons qu’il n’ont pas vécu l’évènement avoir eu un premier enfant au cours de ces trois premières années mais sans savoir ce qu’il adviendra ensuite (fin de l’observation).

Pour réaliser une analyse de survie simple, nous avons donc besoin de deux variables :

une variable évènement qui nous indique si l’individu a vécu ou non l’évènement analysé : le mieux est de la coder sous la forme d’une valeur logique (TRUE si l’évènement a été vécu, FALSE sinon) ou bien sous une forme numérique 0/1 où 0 indique que l’évènement n’a pas été vécu et 1 que l’évènement a été vécu ;
une variable temps qui nous indique le temps écoulé entre l’évènement origine et l’évènement vécu (si l’évènement a eu lieu) ou alors le temps écoulé entre l’évènement origine et la fin de l’observation (censure à droite).

Le package R de référence pour l’analyse de survie est survival.

42.1 Données de l’exemple

Nous allons utiliser le jeu de données gtsummary::trial qui fournit des observations sur 200 patients atteints d’un cancer. La variable death indique si la personne est décédée (1) ou toujours en vie (1) et la variable ttdeath indique en mois la durée entre le diagnostic et le décès ou la censure à droite. Les données sont donc déjà codées de manière à être utilisée dans une analyse de survie.

La variable catégorielle trt indique si le patient a reçu le traitement A ou le traitement B. La variable catégorielle stage correspond au stade du cancer au moment du diagnostic : plus il est élevé plus le cancer est grave et avancé. Enfin, la variable continue age correspond à l’âge révolu du patient au moment du diagnostic.

42.2 Analyse univariée (courbe de Kaplan-Meier)

La courbe de survie de Kaplan-Meier permet de décrire la probabilité de survie au cours du temps tout en tenant compte des éventuelles censures à droite.

Elle se calcule avec la fonction survival::survfit() à laquelle nous allons décrire notre outcome à l’aide de survival::Surv() en lui indiquant d’abord la variable temps puis la variable évènement.

library(gtsummary)
library(survival)
km <- survfit(Surv(ttdeath, death) ~ 1, data = trial)

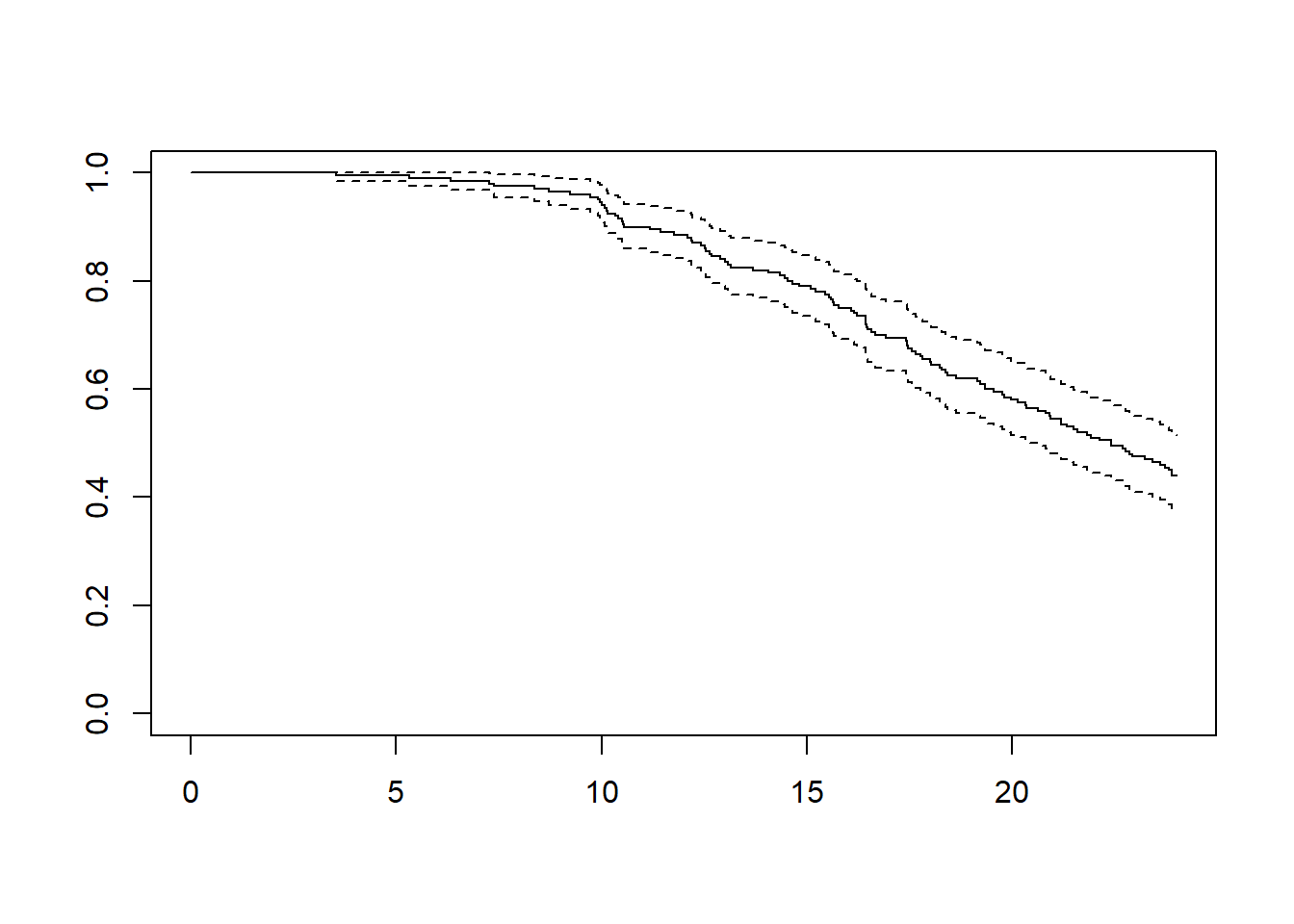
Pour un graphique rapide, on peut utiliser plot().

km |> plot()

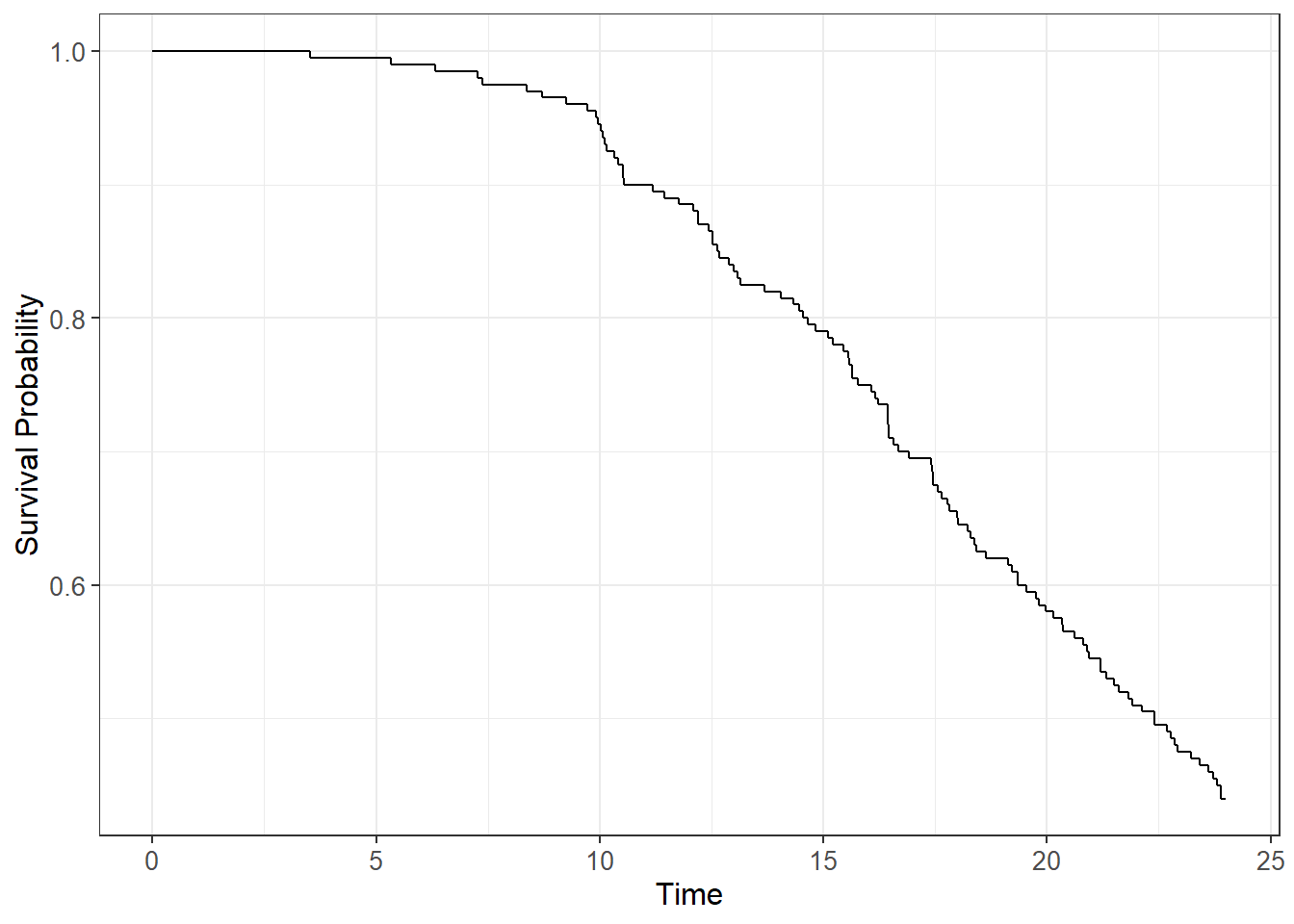
Cependant, il est préférable d’avoir recours au package {ggsurvfit}, développé par le même auteur que gtsummary, et sa fonction homonyme ggsurvfit::ggsurvfit().

library(ggsurvfit)

Loading required package: ggplot2

km |> ggsurvfit()

Le package fournit de multiples options :

ggsurvfit::add_confidence_interval() pour ajouter les intervalles de confiance de la courbe,
ggsurvfit::add_risk_table() pour ajouter une table avec le nombre de personnes encore à risque à chaque pas de temps et le nombre d’évènements,
ggsurvfit::add_quantile() pour ajouter des lignes indiquant un certain quantile (par exemple à quel moment la moitié de la population a connu l’évènement),
ggsurvfit::add_censor_mark() pour ajouter des marques indiquant les censures à droite.

Le graphique renvoyé est un objet ggplot2 et l’on peut appliquer toute fonction graphique additionnelle.

library(ggplot2)
km |> 
  ggsurvfit() +
  add_confidence_interval() +
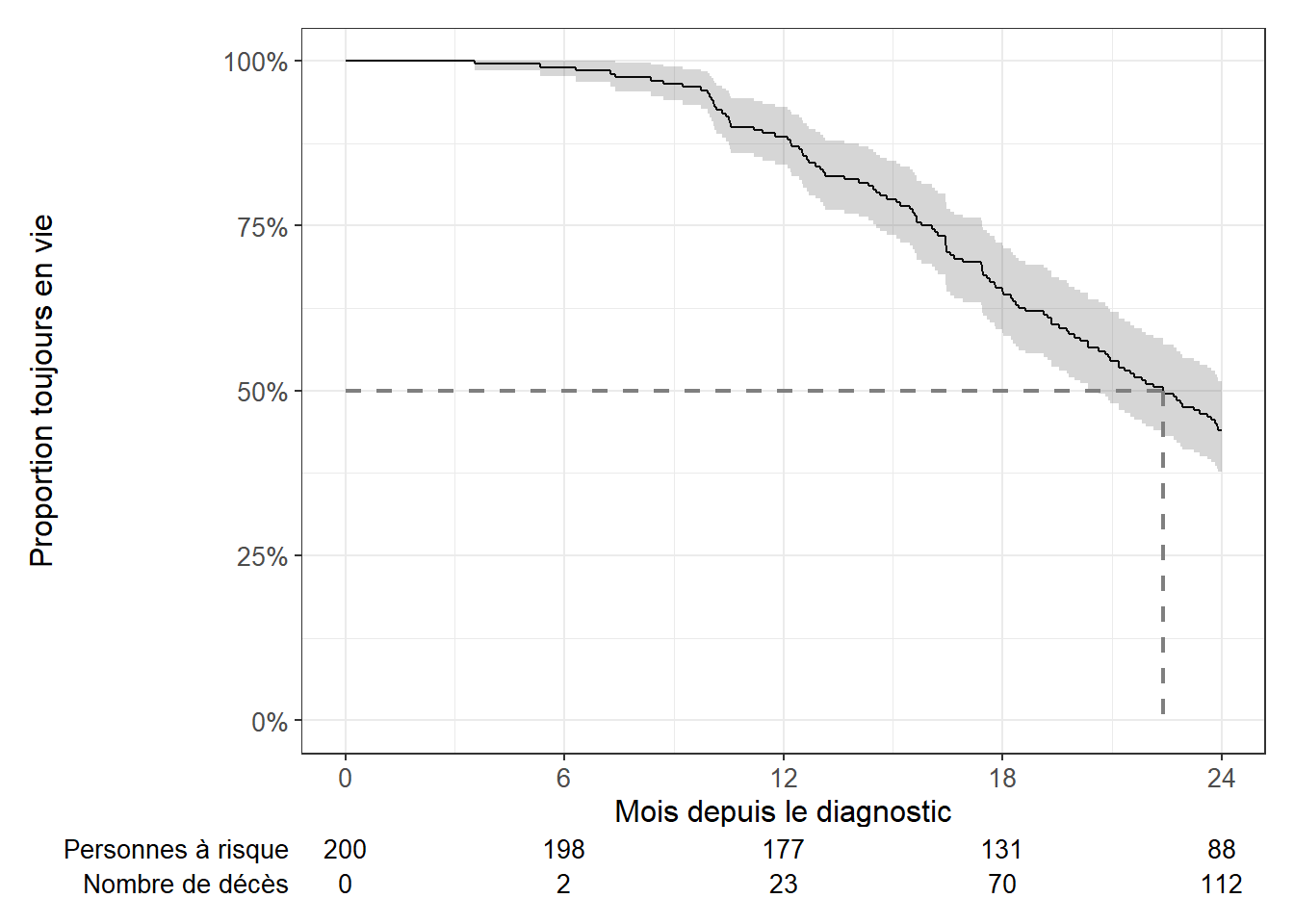
  add_risktable(
    stats_label = list(
      "n.risk" = "Personnes à risque",
      "cum.event" = "Nombre de décès"
    )
  ) +
  add_quantile(
    y_value = 0.5, 
    color = "gray50", 
    linewidth = 0.75
  ) +
  scale_x_continuous(breaks = 0:4*6) +
  scale_y_continuous(labels = scales::percent) +
  xlab("Mois depuis le diagnostic") +
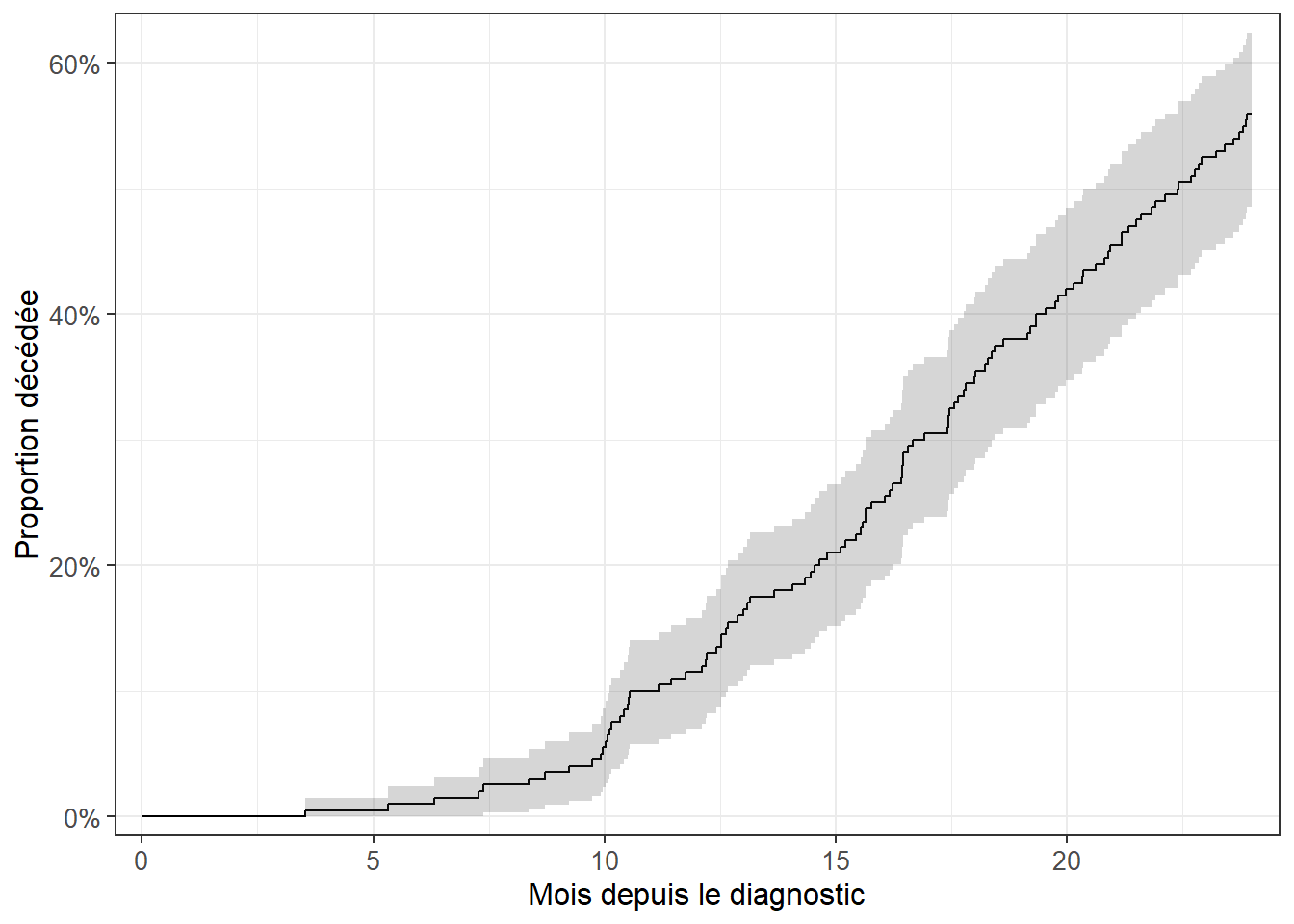
  ylab("Proportion toujours en vie")

Il est également possible de représenter la proportion de personnes ayant vécu l’évènement plutôt que celle ne l’ayant toujours pas vécu.

km |> 
  ggsurvfit(type = "risk") +
  add_confidence_interval() +
  scale_ggsurvfit() +
  xlab("Mois depuis le diagnostic") +
  ylab("Proportion décédée")

Pour un tableau des résultats, on fera appel à gtsummary::tbl_survfit() à laquelle on indiquera soit des points dans le temps, soit une série de quantiles. Par défaut, cela affiche la valeur de la courbe et les intervalles de confiance à 95%.

# affichage des résultats en français
theme_gtsummary_language("fr", decimal.mark = ",")

Setting theme "language: fr"

km |> 
  tbl_survfit(
    times = c(6, 12, 18, 24),
    label_header = "**Mois {time}**"
  )

Caractéristique	Mois 6	Mois 12	Mois 18	Mois 24
Total	99% (98%, 100%)	89% (84%, 93%)	65% (59%, 72%)	44% (38%, 51%)

km |> 
  tbl_survfit(
    probs = c(.25, .5, .75)
  ) |> 
  modify_spanning_header(
    all_stat_cols() ~ "**Proportion décédée**"
  )

Caractéristique	Proportion décédée
Caractéristique	25% Percentile	50% Percentile	75% Percentile
Total	16 (15, 17)	22 (21, —)	— (—, —)

42.3 Analyse bivariée (Kaplan-Meier)

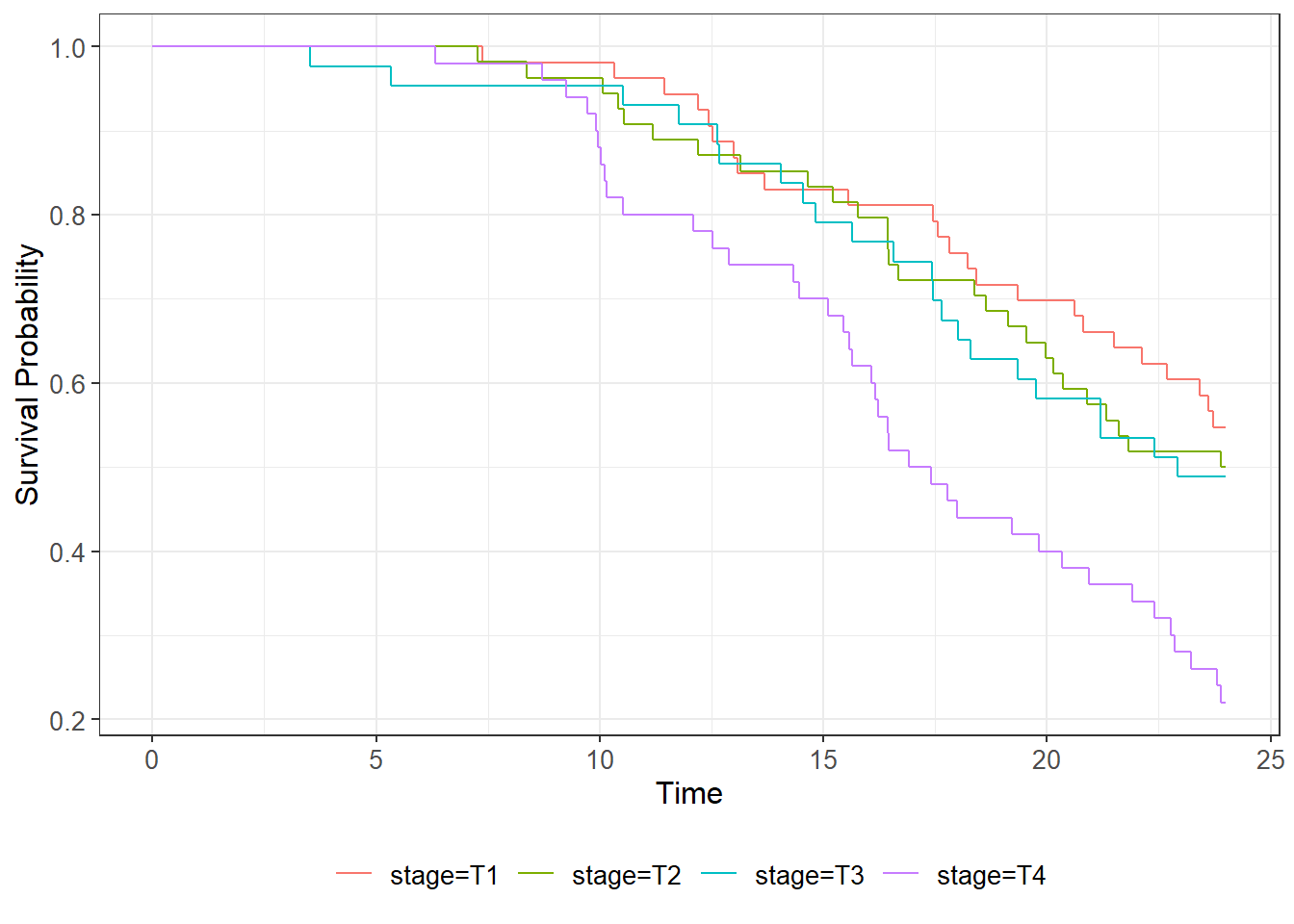
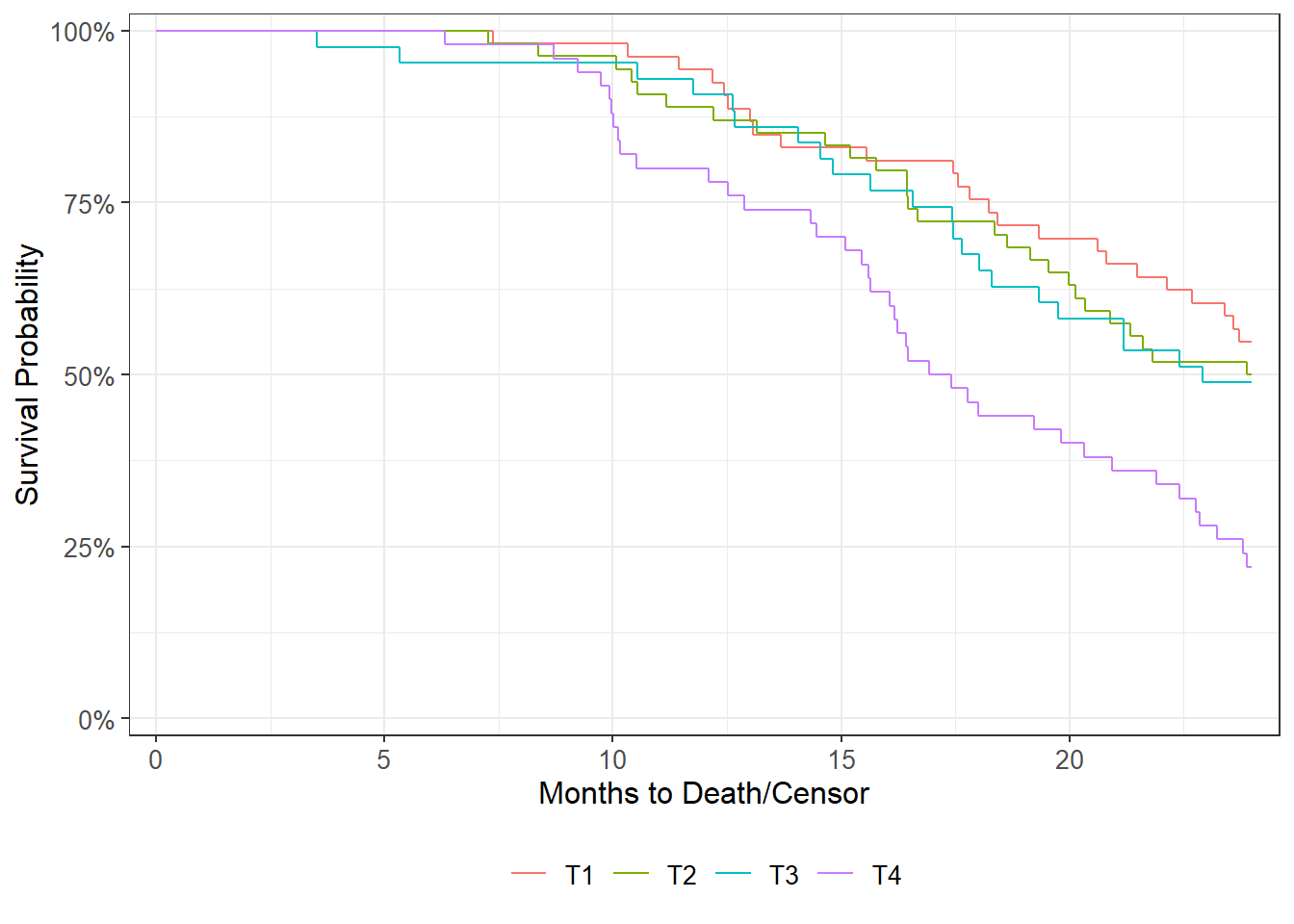
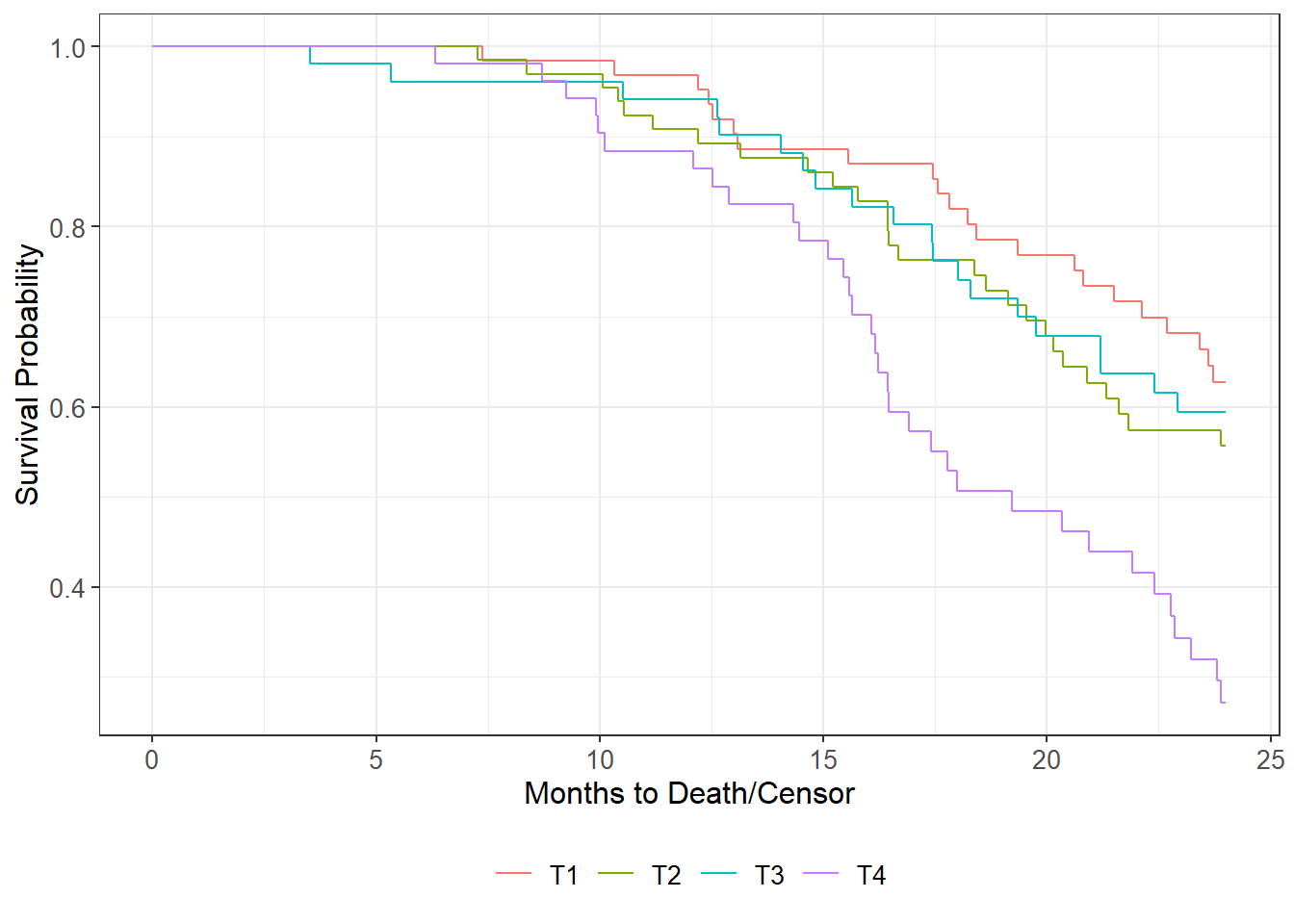
Il est possible de calculer des courbes de Kaplan-Meier selon une variable catégorielle (analyse stratifiée). Par exemple, pour voir comment varie la survie en fonction du stade au diagnostic.

km_stade <- survfit(
  Surv(ttdeath, death) ~ stage,
  data = trial
)
km_stade |> ggsurvfit()

Nous pouvons facilement améliorer le rendu du graphique en utilisant ggsurvfit::surfit2() à la place de survival::survfit(). Les deux fonctions sont équivalentes à l’exception du fait que la version fournie par ggsurvfit concerne certaines informations, comme les étiquettes de variables, afin d’améliorer le rendu visuel par défaut du graphique.

km_stade <- survfit2(
  Surv(ttdeath, death) ~ stage,
  data = trial
)
km_stade |> 
  ggsurvfit() +
  scale_ggsurvfit()

Il est possible de faire un test statistique pour déterminer si les courbes de survie diffèrent selon les stades avec la fonction survival::survdiff() qui implémente le test du log-rank ou de Mantel-Haenszel (par défaut).

survdiff(
  Surv(ttdeath, death) ~ stage,
  data = trial
)

Call:
survdiff(formula = Surv(ttdeath, death) ~ stage, data = trial)

          N Observed Expected (O-E)^2/E (O-E)^2/V
stage=T1 53       24     33.3     2.613      3.73
stage=T2 54       27     31.9     0.750      1.05
stage=T3 43       22     24.8     0.319      0.41
stage=T4 50       39     22.0    13.223     16.56

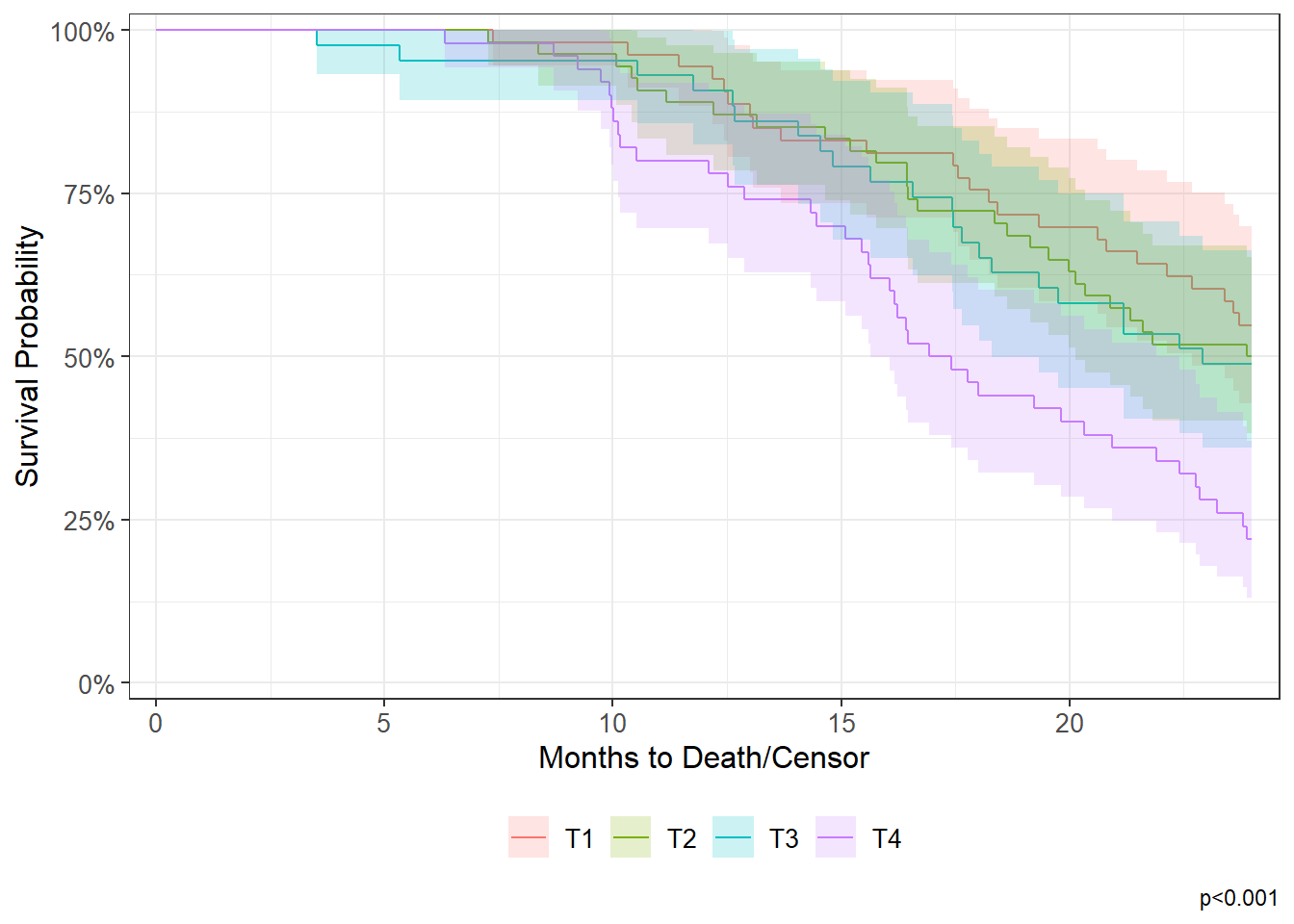
 Chisq= 17  on 3 degrees of freedom, p= 7e-04

Il est possible de calculer et d’afficher directement ce résultat sur le graphique (en bas à droite) avec ggsurvfit::add_pvalue().

km_stade |> 
  ggsurvfit() +
  add_confidence_interval() +
  add_pvalue() +
  scale_ggsurvfit()

Dans un tableau, on aura recours à gtsummary::add_p().

km_stade |> 
  tbl_survfit(times = c(12, 24)) |> 
  add_p() |> 
  bold_labels()

Caractéristique	Temps 12	Temps 24	p-valeur¹
T Stage			<0,001
T1	94% (88%, 100%)	55% (43%, 70%)
T2	89% (81%, 98%)	50% (38%, 65%)
T3	91% (82%, 100%)	49% (36%, 66%)
T4	80% (70%, 92%)	22% (13%, 37%)
¹ Log-rank test

Le diaporama ci-dessous vous permet de visualiser chaque étape d’un code permettant d’afficher des courbes de survie stratifiées.

42.3.1 Courbes de survie bivariées répétées

Il est possible de réaliser simultanément plusieurs analyses de survie bivariées avec tbl_survfit(). La syntaxe est juste un peu différente. Au lieu de passer un objet survfit() à tbl_survfit(), on lui passera le jeu de données et on utilisera y et include pour indiquer comment calculer les courbes de survies.

trial |> 
  tbl_survfit(
    y = Surv(ttdeath, death),
    include = c(stage, trt),
    times = c(12, 24)
  ) |> 
  add_p() |> 
  bold_labels()

Caractéristique	Temps 12	Temps 24	p-valeur¹
T Stage			<0,001
T1	94% (88%, 100%)	55% (43%, 70%)
T2	89% (81%, 98%)	50% (38%, 65%)
T3	91% (82%, 100%)	49% (36%, 66%)
T4	80% (70%, 92%)	22% (13%, 37%)
Chemotherapy Treatment			0,2
Drug A	91% (85%, 97%)	47% (38%, 58%)
Drug B	86% (80%, 93%)	41% (33%, 52%)
¹ Log-rank test

42.4 Analyse multivariable (modèle de Cox)

Pour une analyse multivariable, on aura recours à un modèle de Cox. Il est tout à fait possible d’inclure des variables continues, par exemple l’âge des patients. Ici, nous n’abordons qu’un modèle avec des variables fixes au cours du temps. Mais il est possible de calculer un modèle de Cox avec des variables explicatives pouvant changer au cours du temps.

Le modèle de Cox se calcule avec survival::coxph().

mod <- coxph(
  Surv(ttdeath, death) ~ stage + trt + age,
  data = trial
)

42.4.1 Visualisation des résultats

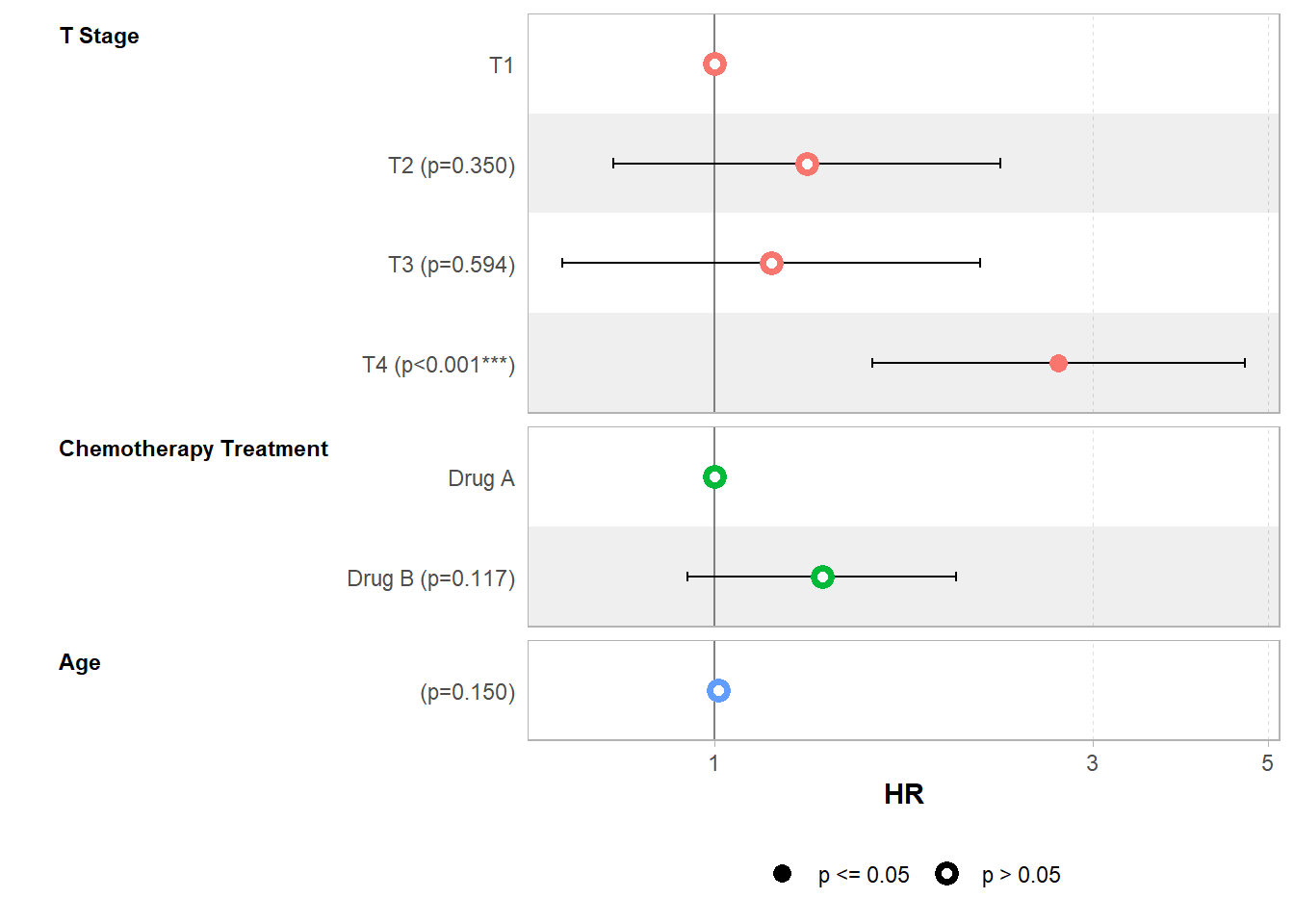
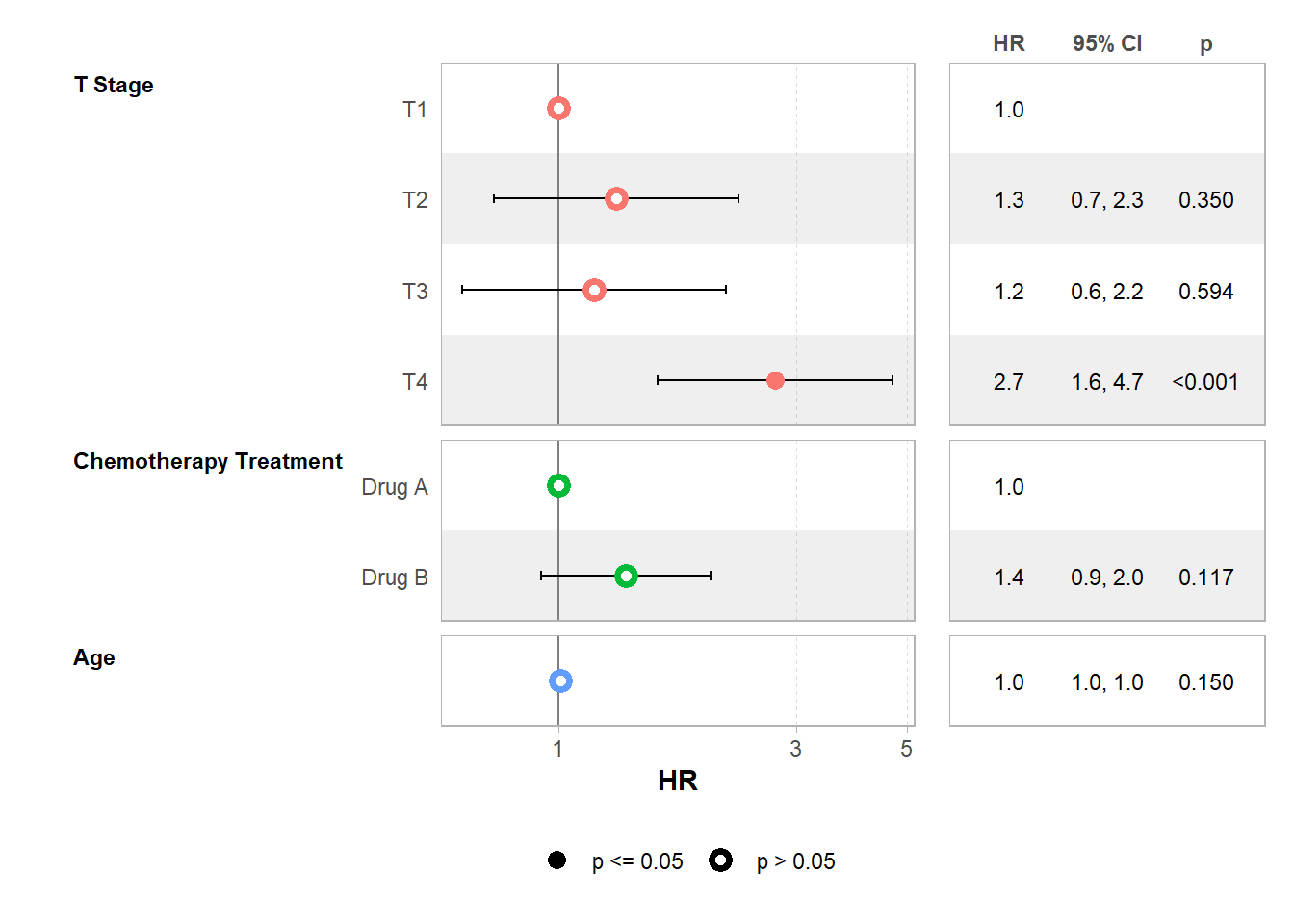
Comme pour la régression logistique (cf. Chapitre 22), nous pouvons utiliser gtsummary::tbl_regression(), ggstats::ggcoef_model() et ggstats::ggcoef_table() pour afficher les coefficients du modèle.

Il est pertinent d’afficher l’exponentielle des coefficients car il s’interprètent comme des risque relatifs ou hazard ratios.

mod |> 
  tbl_regression(exponentiate = TRUE) |> 
  add_global_p(keep = TRUE) |> 
  bold_labels()

Caractéristique	HR¹	95% IC¹	p-valeur
T Stage			0,002
T1	—	—
T2	1,31	0,74 – 2,30	0,4
T3	1,18	0,64 – 2,16	0,6
T4	2,72	1,58 – 4,68	<0,001
Chemotherapy Treatment			0,12
Drug A	—	—
Drug B	1,37	0,93 – 2,02	0,12
Age	1,01	1,00 – 1,02	0,15
¹ HR = rapport de risques instantanés, IC = intervalle de confiance

library(ggstats)
mod |> 
  ggcoef_model(exponentiate = TRUE)

mod |> 
  ggcoef_table(exponentiate = TRUE)

Le risque relatif correspond au rapport des risques instantanés. Il est par exemple de 2,7 pour les personnes au stade T4 par rapport à celles au stade T1. Cela signifie donc qu’à tout moment le risque de décéder est 2,7 fois plus important pour les personnes au stade 4 par rapport à celles au stade 1.

42.4.2 Vérification des hypothèses

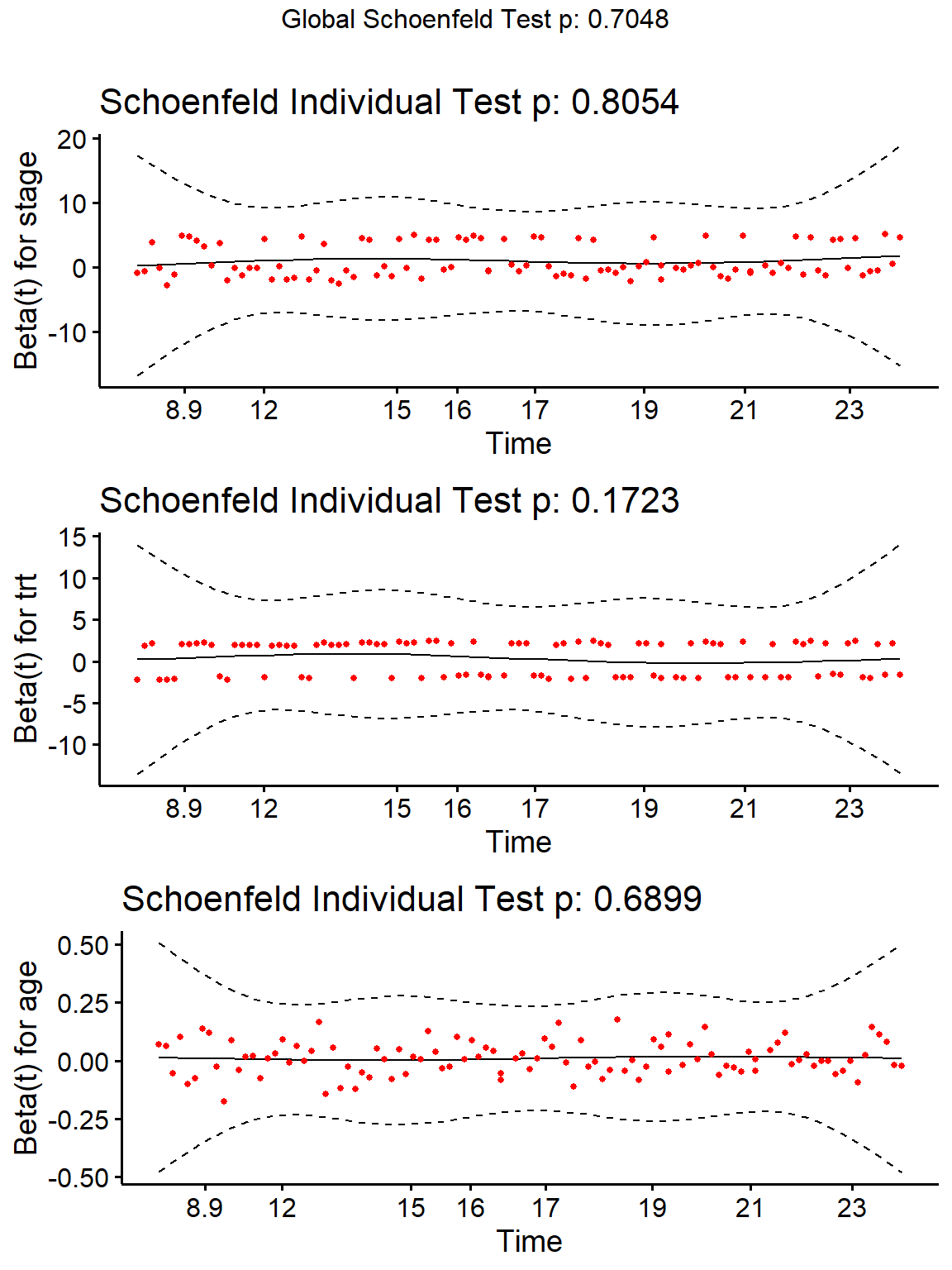
Le modèle de Cox considère que, bien que le risque de décès évolue au cours du temps, les risques relatifs restent quant à eux identiques. Il s’agit de l’hypothèse de la proportionnalité des risques relatifs. Selon cette hypothèse les résidus de Schoenfeld ne dépendent pas du temps. Cette hypothèse peut être testée avec la fonction cox.zph().

mod |> cox.zph()

       chisq df    p
stage  0.983  3 0.81
trt    1.863  1 0.17
age    0.159  1 0.69
GLOBAL 2.969  5 0.70

Un test est ici effectué globalement et pour chaque variable individuellement. Une valeur de p inférieure à 5% indique un problème potentiel en termes de proportionnalité des risques.

La fonction survminer::ggcoxzph() du package survminer permet de représenter les résidus de Schoenfeld et de visualiser si leur répartition est relativement stable au cours du temps (visuellement horizontale autour de 0) ou bien s’ils suivent une autre distribution.

mod |> cox.zph() |> survminer::ggcoxzph()

42.4.3 Représentation graphique d’une courbe de survie ajustée

Il est possible de calculer, avec survfit2(), des courbes de survie ajustées à partir d’un modèle de Cox. Cependant, pour indiquer la variable de stratification des courbes, il est nécessaire de l’inclure avec strata() dans l’appel du modèle de Cox.

trial |> 
  coxph(
    Surv(ttdeath, death) ~ strata(stage) + trt + age,
    data = _
  ) |> 
  survfit2() |> 
  ggsurvfit()

42.4.4 Sélection pas à pas d’un modèle réduit

Pour réduire le modèle (voir Chapitre 23), il est possible d’utiliser la fonction step().

mod |> step()

Start:  AIC=1002.04
Surv(ttdeath, death) ~ stage + trt + age

Error in drop1.default(fit, scope$drop, scale = scale, trace = trace, : le nombre de lignes utilisées a changé : supprimer les valeurs manquantes ?

Dans notre exemple, nous rencontrons une erreur liée à des valeurs manquantes pour l’une des variables explicatives. Comme abordé précédemment (cf. Section 23.8), nous pouvons avoir recours à la fonction step_with_na() de notre cru.

step_with_na <- function(model,
                         full_data = eval(model$call$data),
                         ...) {
  # data with no NAs
  if (is.null(full_data)) {
    ...data_no_na <- model.frame(model)
  } else {
    ...data_no_na <- get_all_vars(model, data = full_data) |> na.omit()
  }
  
  # assign ...data_no_na in parent.frame()
  assign("...data_no_na", ...data_no_na, envir = parent.frame())
  
  # refit the model without NAs
  model_no_na <- update(
    model,
    formula = terms(model),
    data = ...data_no_na
  )
  
  # apply step()
  model_simplified <- step(model_no_na, ...)
  
  # recompute simplified model using full data
  if (is.null(full_data)) {
    update(
      model,
      formula = terms(model_simplified)
    )
  } else {
    update(
      model,
      formula = terms(model_simplified),
      data = full_data
    )
  }
}

Il y a néanmoins une petite subtilité pour l’utiliser ici. En effet, elle a besoin de pouvoir reconstruire notre outcome qui est ici une variable composée créée avec Surv(). Deux possibilités. La première consiste à transmettre à step_with_na() le jeu de données complet.

mod |> step_with_na(full_data = trial)

Start:  AIC=1002.04
Surv(ttdeath, death) ~ stage + trt + age

        Df    AIC
<none>     1002.0
- age    1 1002.1
- trt    1 1002.5
- stage  3 1011.2

Call:
coxph(formula = Surv(ttdeath, death) ~ stage + trt + age, data = full_data)

              coef exp(coef) se(coef)     z        p
stageT2   0.268596  1.308126 0.287412 0.935 0.350028
stageT3   0.164980  1.179370 0.309897 0.532 0.594468
stageT4   1.000324  2.719163 0.276830 3.614 0.000302
trtDrug B 0.312336  1.366614 0.199005 1.569 0.116535
age       0.010305  1.010358 0.007154 1.440 0.149753

Likelihood ratio test=17.98  on 5 df, p=0.002975
n= 189, number of events= 103 
   (11 observations effacées parce que manquantes)

La seconde consiste à créer notre outcome en amont du calcul du modèle.

trial <- trial |> 
  mutate(survie = Surv(ttdeath, death))
mod2 <- coxph(
  survie ~ stage + trt + age,
  data = trial
)
mod2 |> step_with_na()

Start:  AIC=1002.04
survie ~ stage + trt + age

        Df    AIC
<none>     1002.0
- age    1 1002.1
- trt    1 1002.5
- stage  3 1011.2

Call:
coxph(formula = survie ~ stage + trt + age, data = full_data)

              coef exp(coef) se(coef)     z        p
stageT2   0.268596  1.308126 0.287412 0.935 0.350028
stageT3   0.164980  1.179370 0.309897 0.532 0.594468
stageT4   1.000324  2.719163 0.276830 3.614 0.000302
trtDrug B 0.312336  1.366614 0.199005 1.569 0.116535
age       0.010305  1.010358 0.007154 1.440 0.149753

Likelihood ratio test=17.98  on 5 df, p=0.002975
n= 189, number of events= 103 
   (11 observations effacées parce que manquantes)

42.4.5 Modèles de Cox univariables

Comme déjà abordé dans le chapitre sur la régression logistique binaire, il est possible d’effectuer en une fois plusieurs modèles univariables avec gtsummary::tbl_uvregression() (cf. Section 22.9).

trial |> 
  tbl_uvregression(
    method = coxph,
    y = Surv(ttdeath, death),
    include = c(stage, trt, age),
    exponentiate = TRUE
  ) |> 
  bold_labels()

Caractéristique	N	HR¹	95% IC¹	p-valeur
T Stage	200
T1		—	—
T2		1,18	0,68 – 2,04	0,6
T3		1,23	0,69 – 2,20	0,5
T4		2,48	1,49 – 4,14	<0,001
Chemotherapy Treatment	200
Drug A		—	—
Drug B		1,25	0,86 – 1,81	0,2
Age	189	1,01	0,99 – 1,02	0,3
¹ HR = rapport de risques instantanés, IC = intervalle de confiance

42.5 Analyse de survie pondérée

Lorsque l’on travaille avec des données pondérées et un plan d’échantillonnage complexe, le plus pertinent est d’avoir recours au package survey (cf. Chapitre 28) qui propose des fonctions adaptées à l’analyse de survie.

Pour l’exemple, nous allons transformer le jeu de données en objet survey en indiquant simplement des poids uniformes égaux à 1, dans la mesure où ce jeux de données n’a pas de poids.

library(survey)

Le chargement a nécessité le package : grid

Le chargement a nécessité le package : Matrix


Attachement du package : 'survey'

L'objet suivant est masqué depuis 'package:graphics':

    dotchart

strial <- svydesign(~ 1, data = trial, weights = ~ 1)

42.5.1 Courbes de Kaplan-Meier

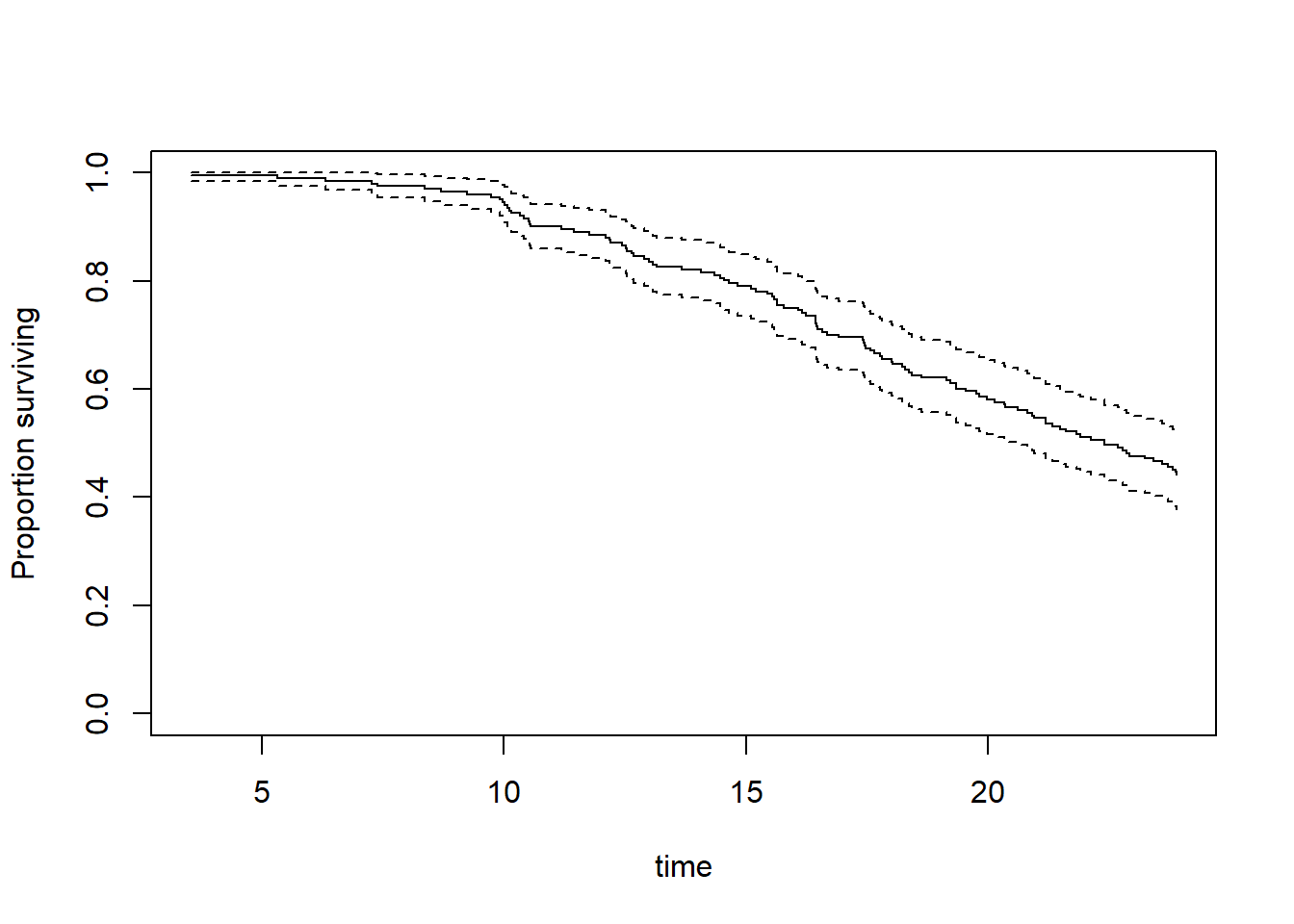
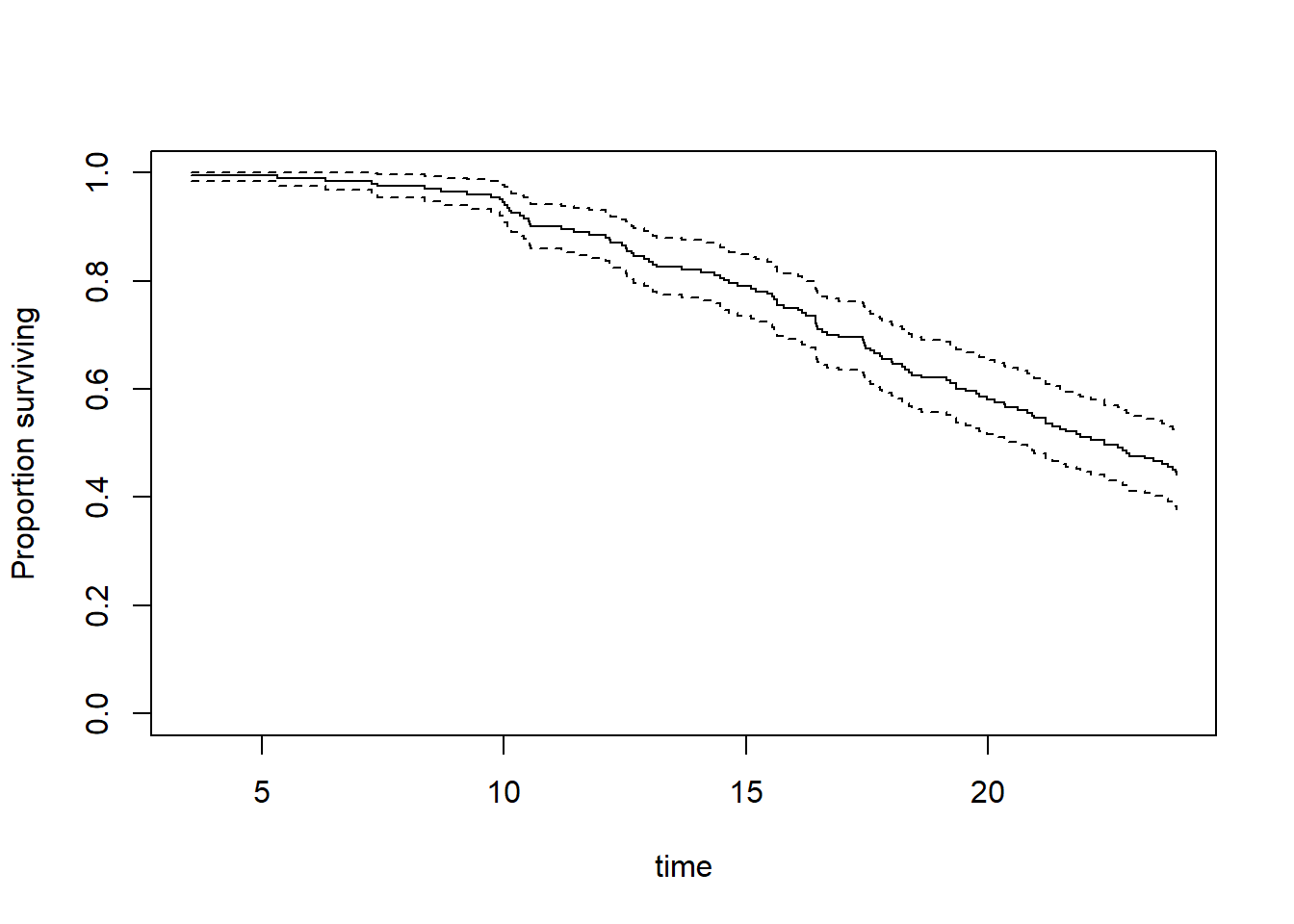
Pour le calcul d’une courbe de Kaplan-Meier, nous allons utiliser la fonction survey::svykm().

Il est préférable de préciser se = TRUE pour que les erreurs standards soient calculées, ce qui permettra plus tard de récupérer les intervalles de confiance. Attention : sur un gros jeu de données, ce temps de calcul peut être très long (plusieurs minutes ou dizaines de minutes).

skm <- svykm(
  Surv(ttdeath, death) ~ 1,
  design = strial,
  se = TRUE
)
skm_trt <- svykm(
  Surv(ttdeath, death) ~ trt,
  design = strial,
  se = TRUE
)

Malheureusement, ggsurvfit::ggsurvfit() et gtsummary::tbl_survfit() ne sont pas (encore ?) compatibles avec les courbes de survies créées avec survey::svykm(). On devra donc avoir recours aux fonctions de bases.

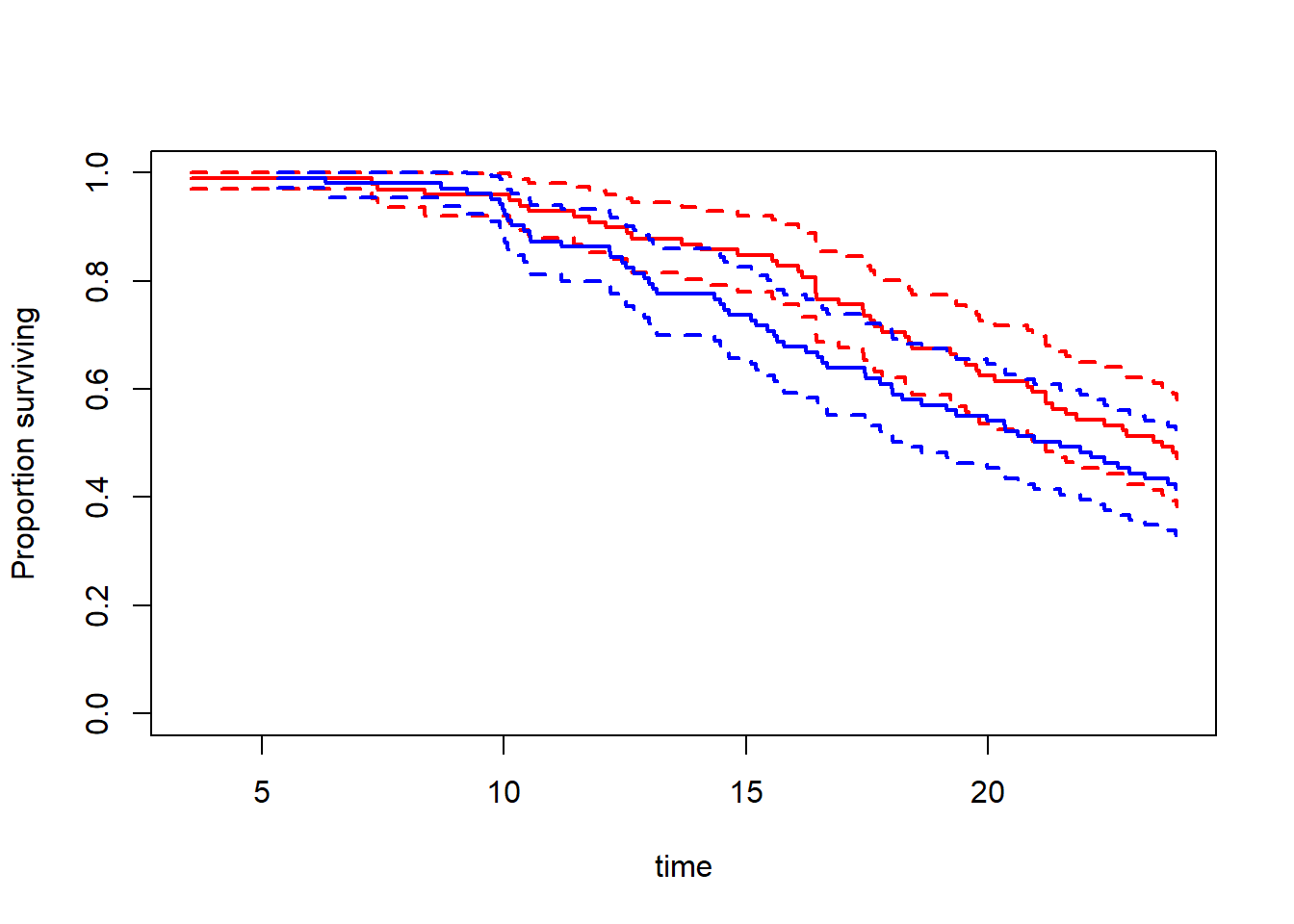
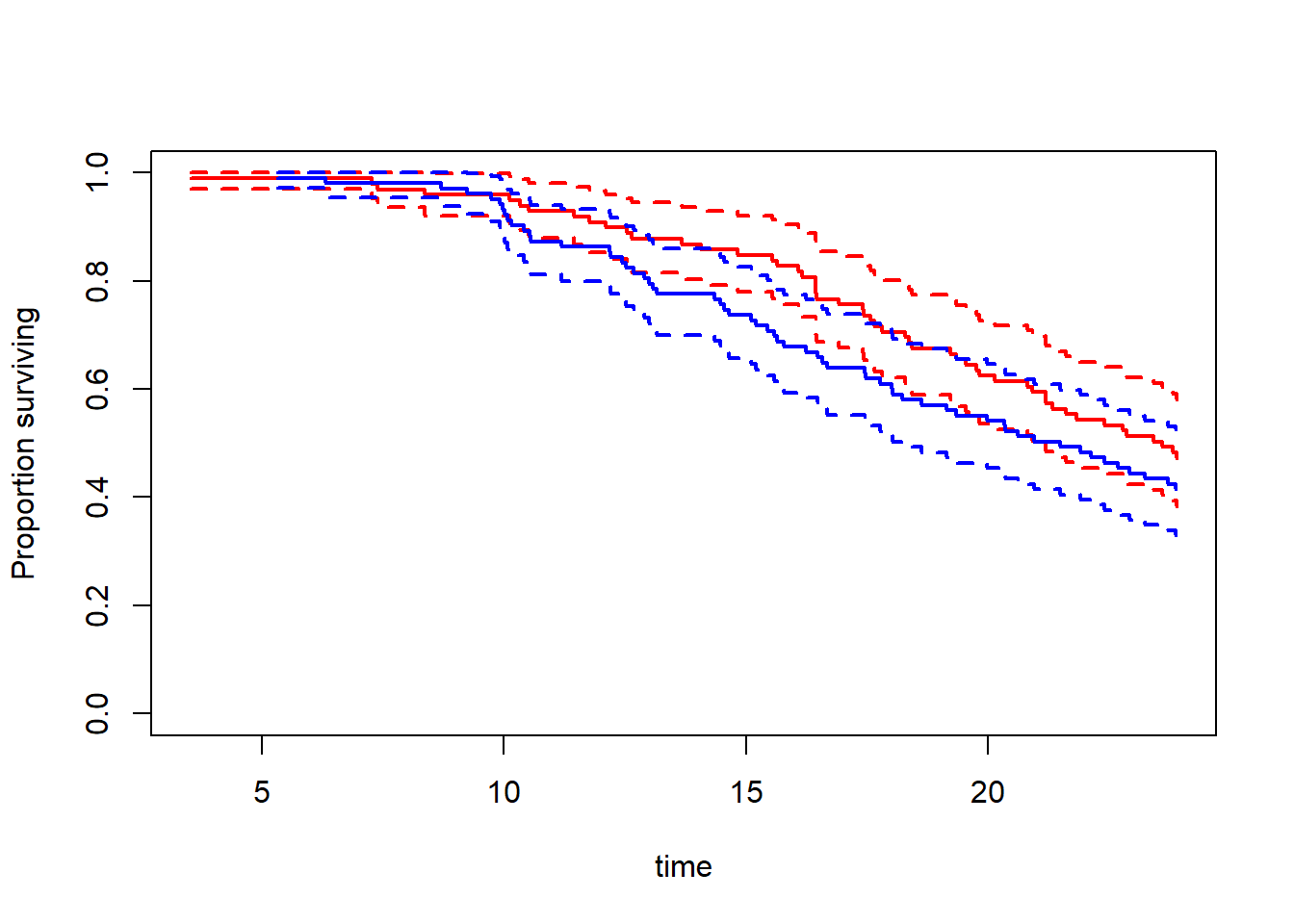
Pour un graphique avec affichage des intervalles de confiance :

skm |>  plot(ci = TRUE)

skm_trt |> plot(
  ci = TRUE,
  pars = list(
    col = c("red", "blue")
  ),
  lwd = 2
)

On pourra aussi avoir recours au package jskm et sa fonction jskm::svyjskm().

library(jskm)
skm_trt |> svyjskm()

skm_trt |> 
  svyjskm(
    pval = TRUE,
    xlabs = "Mois depuis le diagnostic",
    ylabs = "Probabilité de survie",
    surv.scale = "percent",
    ci = TRUE,
    table = TRUE,
    label.nrisk = "Personnes à risque"
  )

La fonction quantile() peut-être appliquée à une courbe de survie simple (ici skm) mais dans le cadre d’une courbe de survie stratifiée (ici skm_trt) il faut l’appliquer à chaque sous-élément. On pourra alors s’aider de la petite fonction ci-dessous (utiliser ci_level = NULL pour ne pas calculer les intervalles de confiance.

svykm_probs <- function(x,
                        probs = c(1, .75, 5, .25),
                        ci_level = .95,
                        strata = NULL) {
  if (inherits(x, "svykm")) {
    if (is.null(ci_level) | is.null(x$varlog)) {
      res <- quantile(x, probs, ci = FALSE) |> 
        dplyr::as_tibble(rownames = "prob")
    } else {
      tmp <- quantile(
        x,
        probs,
        ci = TRUE,
        level = ci_level
      )
      ci <- attr(tmp, "ci") |> 
        dplyr::as_tibble(rownames = "prob") |> 
        dplyr::rename(conf.low = 2, conf.high = 3)
      res <- tmp |> 
        dplyr::as_tibble(rownames = "prob") |> 
        dplyr::left_join(ci, by = "prob")
    }
    if (!is.null(strata))
      res$strata <- strata
    res
  } else {
    x |> 
      seq_along() |> 
      lapply(
        \(i) {
          svykm_probs(
            x[[i]],
            probs = probs,
            ci_level = ci_level,
            strata = names(x)[[i]]
          )
        }
      ) |> 
      dplyr::bind_rows()
  }
}

Ainsi :

skm |> svykm_probs()

# A tibble: 4 × 4
  prob   value conf.low conf.high
  <chr>  <dbl>    <dbl>     <dbl>
1 1       3.53     3.53      7.27
2 0.75   16.1     14.5      17.4 
3 5       3.53     3.53      3.53
4 0.25  Inf      Inf       Inf

skm_trt |> svykm_probs(probs = c(1, .8, .6, .4))

# A tibble: 8 × 5
  prob   value conf.low conf.high strata
  <chr>  <dbl>    <dbl>     <dbl> <chr> 
1 1       3.53     3.53      8.37 Drug A
2 0.8    16.4     14.1      18.3  Drug A
3 0.6    20.9     18.4      23.8  Drug A
4 0.4   Inf       23.8     Inf    Drug A
5 1       5.33     5.33      9.24 Drug B
6 0.8    13       11.2      15.6  Drug B
7 0.6    18.0     15.8      21.5  Drug B
8 0.4   Inf       21.9     Inf    Drug B

On ne peut pas facilement accéder aux valeurs de la courbe de survie à certains points de temps. Mais la fonction suivante permets de la faire aisément. Il faut lui passer, via times, une liste de points de temps.

svykm_times <- function(x,
                        times,
                        ci_level = .95,
                        strata = NULL) {
  if (inherits(x, "svykm")) {
    idx <- sapply(
      times,
      function(t) max(which(x$time <= t))
    )
    if (is.null(ci_level) | is.null(x$varlog)) {
      res <- dplyr::tibble(
        time = times,
        value = x$surv[idx]
      )
    } else {
      ci <- confint(x, parm = times, level = ci_level)
      res <- dplyr::tibble(
        time = times,
        value = x$surv[idx],
        conf.low = ci[, 1],
        conf.high = ci[, 2]
      )
    }  
    if (!is.null(strata))
      res$strata <- strata
    res
  } else {
    x |> 
      seq_along() |> 
      lapply(
        \(i) {
          svykm_times(
            x[[i]],
            times = times,
            ci_level = ci_level,
            strata = names(x)[[i]]
          )
        }
      ) |> 
      dplyr::bind_rows()
  }
}

skm |> svykm_times(c(5, 10, 15, 20))

# A tibble: 4 × 4
   time value conf.low conf.high
  <dbl> <dbl>    <dbl>     <dbl>
1     5 0.995    0.985     1    
2    10 0.945    0.914     0.977
3    15 0.791    0.736     0.849
4    20 0.581    0.517     0.653

skm_trt |> svykm_times(c(5, 10, 15, 20))

Warning in max(which(x$time <= t)): aucun argument pour max ; -Inf est renvoyé

Warning in max(which(object$time <= t)): aucun argument pour max ; -Inf est
renvoyé

# A tibble: 8 × 5
   time  value conf.low conf.high strata
  <dbl>  <dbl>    <dbl>     <dbl> <chr> 
1     5  0.990    0.970     1     Drug A
2    10  0.959    0.921     0.999 Drug A
3    15  0.848    0.780     0.921 Drug A
4    20  0.624    0.536     0.727 Drug A
5     5 NA       NA        NA     Drug B
6    10  0.932    0.884     0.982 Drug B
7    15  0.737    0.656     0.827 Drug B
8    20  0.541    0.453     0.647 Drug B

42.5.2 Modèle de Cox

Pour le modèle de Cox, on aura recours à la fonction survey::svycoxph().

mods <- svycoxph(
  Surv(ttdeath, death) ~ stage + trt + age,
  design = strial
)

Cette fois-ci, il est possible d’utiliser gtsummary::tbl_regression() ou ggstats::ggcoef_model() sans problème.

mods |> 
  tbl_regression(exponentiate = TRUE) |> 
  bold_labels()

Independent Sampling design (with replacement)
svydesign(~1, data = trial, weights = ~1)

Caractéristique	HR¹	95% IC¹	p-valeur
stage
T1	—	—
T2	1,31	0,75 – 2,28	0,3
T3	1,18	0,64 – 2,19	0,6
T4	2,72	1,60 – 4,63	<0,001
trt
Drug A	—	—
Drug B	1,37	0,93 – 2,01	0,11
age	1,01	1,00 – 1,03	0,2
¹ HR = rapport de risques instantanés, IC = intervalle de confiance

Enfin, pour le test de l’hypothèse de proportionnalité des risques, on peut utiliser comme précédemment la fonction cox.zph().

mods |> cox.zph()

          chisq df    p
stage  0.004915  3 1.00
trt    0.009315  1 0.92
age    0.000796  1 0.98
GLOBAL 0.014845  5 1.00

42.6 webin-R

L’analyse de survie est présentée sur YouTube dans le webin-R #15 (Analyse de survie).

42.7 Lectures complémentaires

Introduction à l’analyse de survie, courbe de Kaplan-Meier et Introduction au modèle à risque proportionnel de Cox sur la chaîne YouTube “EpiMed Open Course”.
Introduction à l’analyse des durée de survie par Philippe Saint Pierre de l’université de Toulouse (cours assez technique avec formalisme mathématique)
Les cours du Master 2 : Modélisation en pharmacologie clinique et épidémiologique de l’université de Nantes qui abordent des modèles plus complexes (modèles à risques compétitifs, modèles de fragilité, modèles additifs, variables dépendantes du temps, modèles mixtes…) avec des illustrations sous R.