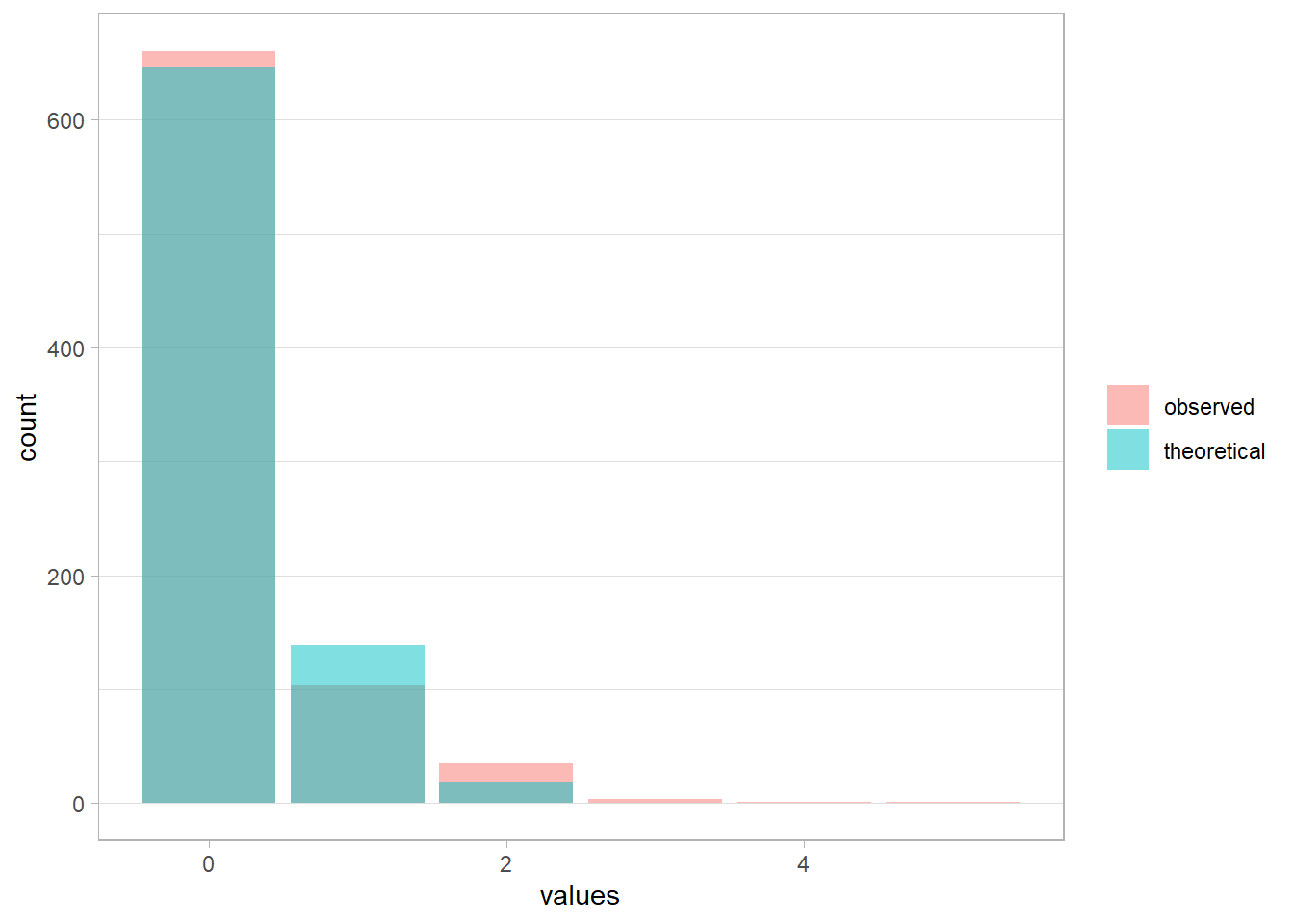43  Modèles de comptage (Poisson & apparentés)

Une variable de type comptage correspond à un outcome (variable à expliquer) entier positif. Le plus souvent, il s’agit du nombre d’occurrences de l’évènement d’intérêt. Pour expliquer une variable de ce type, les modèles linéaires ou les régressions logistiques ne sont pas adaptées. On aura alors recours à des modèles ou régressions de Poisson, c’est-à-dire de manière plus spécifique à un modèle linéaire généralisé (GLM en anglais), avec une fonction de lien logarithmique et une distribution statistique de Poisson.

Les modèles de Poisson font l’hypothèse que la variance est égale à la moyenne, ce qui ne s’observe pas toujours. Auquel cas on aura alors un problème de surdispersion. Dans ce cas-là, nous pourrons avoir recours à des modèles apparentés aux modèles de Poisson, à savoir les modèles quasi-Poisson, les modèles binomiaux négatifs.

Les modèles de comptage peuvent aussi être utiliser pour un outcome binaire, en lieu et place d’une régression logistique, afin d’estimer des prevalence ratios plutôt que des odds ratios.

Enfin, lorsqu’il y a un nombre important de 0 dans les données à expliquer, on peut avoir recours à des modèles zero-inflated ou des modèles hurdle qui, d’une certaine manière, combinent deux modèles en un (d’une part la probabilité de vivre l’évènement et d’autre part le nombre d’occurrences de l’évènement).

43.1 Modèle de Poisson

Nous allons nous intéresser à un premier exemple démographique en nous intéressant à la descendance atteinte par des femmes à l’âge de 30 ans.

43.1.1 Préparation des données du premier exemple

Pour cet exemple, nous allons considérer le jeu de données fecondite fourni par le package questionr. Ce jeu de données comprends trois tables de données (menages, femmes et enfants) simulant les résultats d’une enquête démographique et de santé (EDS). Chargeons les données et jetons y un œil avec labelled::look_for().

library(tidyverse)
library(labelled)
data("fecondite", package = "questionr")
enfants |> look_for()
 pos variable       label                        col_type missing values      
 1   id_enfant      Identifiant de l'enfant      dbl      0                   
 2   id_femme       Identifiant de la mère       dbl      0                   
 3   date_naissance Date de naissance            date     0                   
 4   sexe           Sexe de l'enfant             dbl+lbl  0       [1] masculin
                                                                  [2] féminin 
 5   survie         L'enfant est-il toujours en~ dbl+lbl  0       [0] non     
                                                                  [1] oui     
 6   age_deces      Age au décès (en mois)       dbl      1442

Comme nous pouvons le voir, les variables catégorielles sont codées sous la forme de vecteurs numériques labellisés (cf. Chapitre 12), comme cela aurait été le cas si nous avions importé un fichier Stata ou SPSS avec haven. Première étape, nous allons convertir à la volée ces variables catégorielles en facteurs avec labelled::unlabelled().

femmes <- 
  femmes |> 
  unlabelled()
enfants <- 
  enfants |> 
  unlabelled()

Pour notre analyse, nous allons devoir compter le nombre d’enfants que chaque femme a eu avant l’âge de 30 ans exacts. En premier lieu, nous devons calculer l’âge (cf. Section 34.4) de la mère à la naissance dans le tableau enfants, à l’aide de la fonction lubridate::time_length().

enfants <-
  enfants |>
  left_join(
    femmes |>
      select(id_femme, date_naissance_mere = date_naissance),
    by = "id_femme"
  ) |>
  mutate(
    age_mere = time_length(
      date_naissance_mere %--% date_naissance,
      unit = "years"
    )
  )

Comptons maintenant, par femme, le nombre d’enfants nés avant l’âge de 30 ans et ajoutons cette valeur à la table femmes. N’oublions, après la fusion, de recoder les valeurs manquantes NA en 0 avec tidyr::replace_na().

femmes <-
  femmes |> 
  left_join(
    enfants |> 
      filter(age_mere < 30) |> 
      group_by(id_femme) |> 
      count(name = "enfants_avt_30"),
    by = "id_femme"
  ) |> 
  tidyr::replace_na(list(enfants_avt_30 = 0L))

Il nous reste à calculer l’âge des femmes au moment de l’enquête. Nous allons en profiter pour recoder (cf. Section 9.3) la variable éducation en regroupant les modalités secondaire et supérieur.

femmes <-
  femmes |> 
  mutate(
    age = time_length(
      date_naissance %--% date_entretien,
      unit = "years"
    ),
    educ2 = educ |> 
      fct_recode(
        "secondaire/supérieur" = "secondaire",
        "secondaire/supérieur" = "supérieur"
      )
  )

Enfin, pour l’analyse, nous n’allons garder que les femmes âgées d’au moins 30 ans au moment de l’enquête. En effet, les femmes plus jeunes n’ayant pas encore atteint 30 ans, nous ne connaissons pas leur descendance atteinte à cet âge.

femmes30p <- 
  femmes |> 
  filter(age >= 30)

43.1.2 Calcul & Interprétation du modèle de Poisson

Les modèles de Poisson font partie de la famille des modèles linéaires généralisés (GLM en anglais) et se calculent dont avec la fonction stats::glm() en précisant family = poisson.

mod1_poisson <- glm(
  enfants_avt_30 ~ educ2 + milieu + region,
  family = poisson,
  data = femmes30p
)

L’ensemble des fonctions et méthodes applicables aux modèles GLM, que nous avons déjà abordé dans le chapitre sur la régression logistique (cf. Chapitre 22), peuvent s’appliquer également aux modèles de Poisson. Nous pouvons par exemple réduire notre modèle par minimisation de l’AIC avec stats::step().

mod1_poisson <- step(mod1_poisson)
Start:  AIC=1013.81
enfants_avt_30 ~ educ2 + milieu + region

         Df Deviance    AIC
- region  3   686.46 1010.6
<none>        683.62 1013.8
- milieu  1   686.84 1015.0
- educ2   2   691.10 1017.3

Step:  AIC=1010.65
enfants_avt_30 ~ educ2 + milieu

         Df Deviance    AIC
<none>        686.46 1010.6
- milieu  1   691.30 1013.5
- educ2   2   693.94 1014.1

Par défaut, les modèles de Poisson utilisent une fonction de lien logarithmique (log). Dès lors, il est fréquent de ne pas présenter directement les coefficients du modèle, mais plutôt l’exponentielle de leurs valeurs qui peut s’interpréter comme des risques relatifs (relative risks ou RR)1. L’exponentielle des coefficients peut aussi être appelée incidence rate ratio (IRR) car la régression de Poisson peut également être utilisée pour des modèles d’incidence, qui seront abordés dans le prochain chapitre (cf. Chapitre 44).

1 À ne pas confondre avec les odds ratio ou OR de la régression logistique.

Pour un tableau mis en forme des coefficients, on aura tout simplement recours à gtsummary et sa fonction gtsummary::tbl_regression().

library(gtsummary)
theme_gtsummary_language("fr", decimal.mark = ",", big.mark = " ")
Setting theme `language: fr`
mod1_poisson |> 
  tbl_regression(exponentiate = TRUE) |> 
  bold_labels()
Caractéristique IRR1 95% IC1 p-valeur
Niveau d'éducation


    aucun — —
    primaire 1,25 0,90 – 1,72 0,2
    secondaire/supérieur 0,53 0,27 – 0,96 0,052
Milieu de résidence


    urbain — —
    rural 1,42 1,04 – 1,98 0,032
1 IRR = rapport de taux d’incidence, IC = intervalle de confiance
Table 43.1: Tableau des coefficients du modèle de Poisson

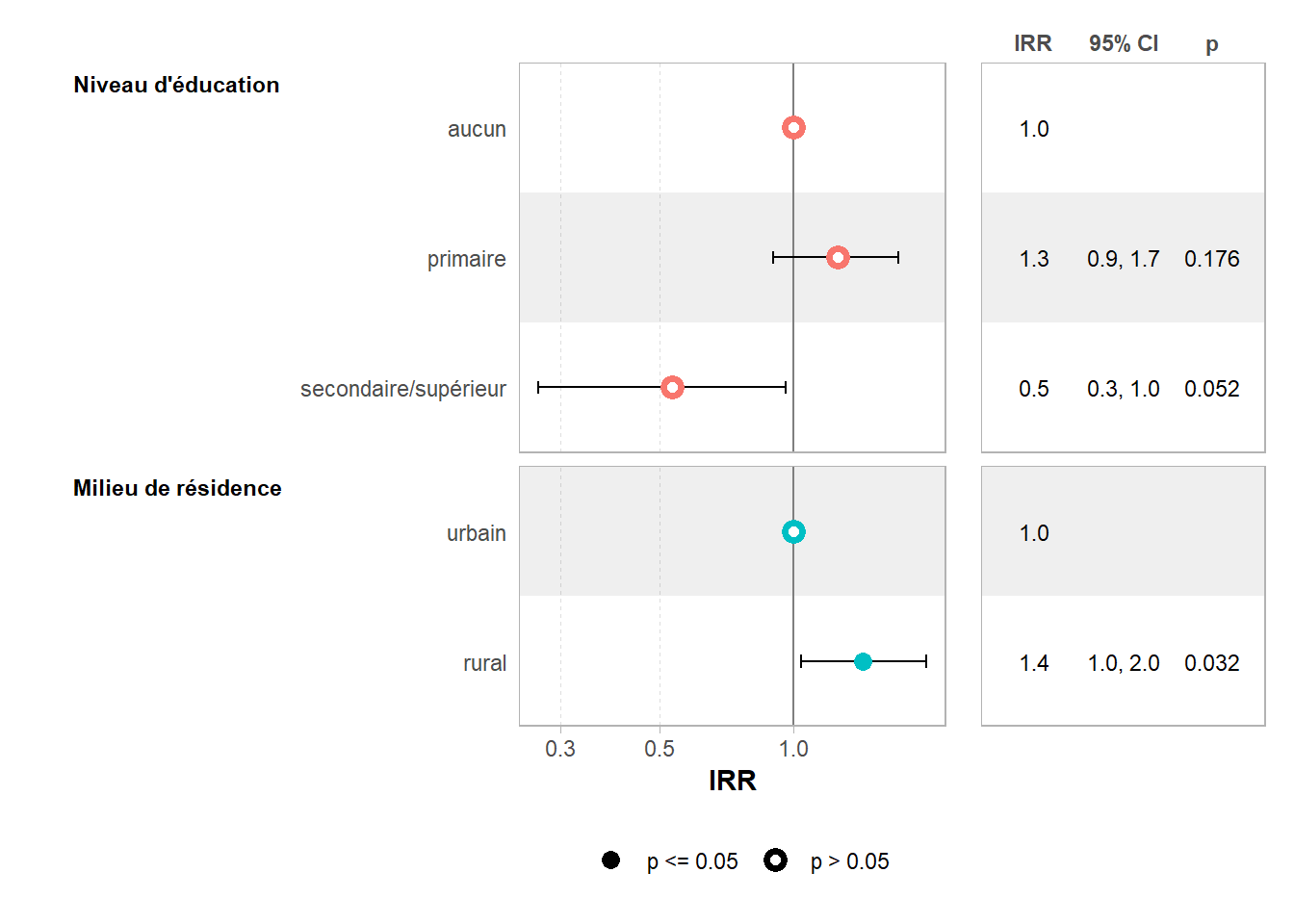
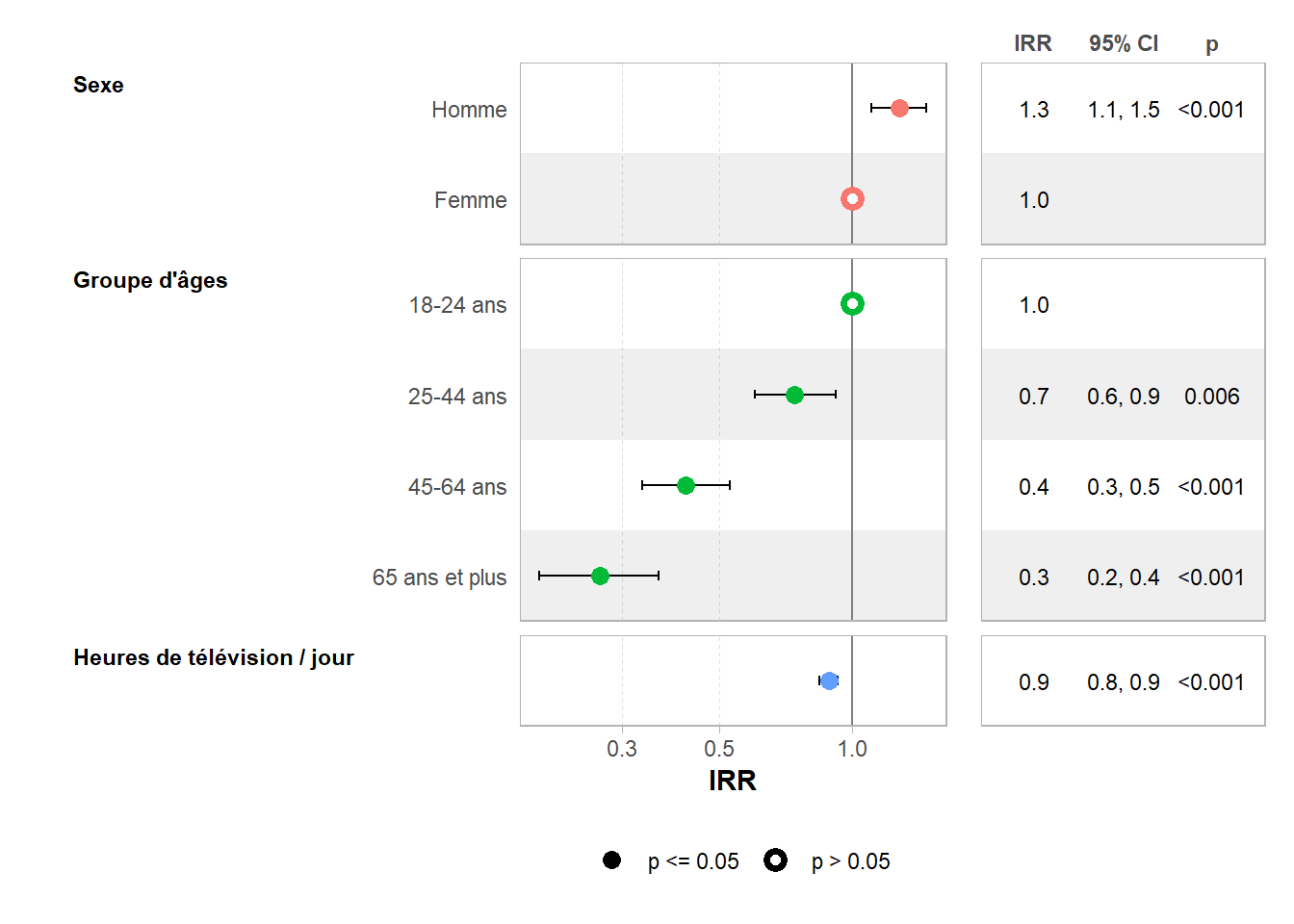
Pour une représentation graphique, on pourra avoir recours à ggstats::ggcoef_model() ou ggstats::ggcoef_table().

library(ggstats)
mod1_poisson |> 
  ggcoef_table(exponentiate = TRUE)
Figure 43.1: Forest plot des coefficients du modèle de Poisson

Pour interpréter les coefficients, il faut se rappeler que ce qui est modéliser dans le modèle de Poisson est le nombre moyen d'évènements. Le RR pour la modalité secondaire/supérieur est de 0,5 : cela signifie donc que, indépendamment des autres variables du modèle, la descendance atteinte à 30 ans moyenne des femmes de niveau secondaire ou supérieure est moitié moindre que cela des femmes sans niveau d’éducation (modalité de référence).

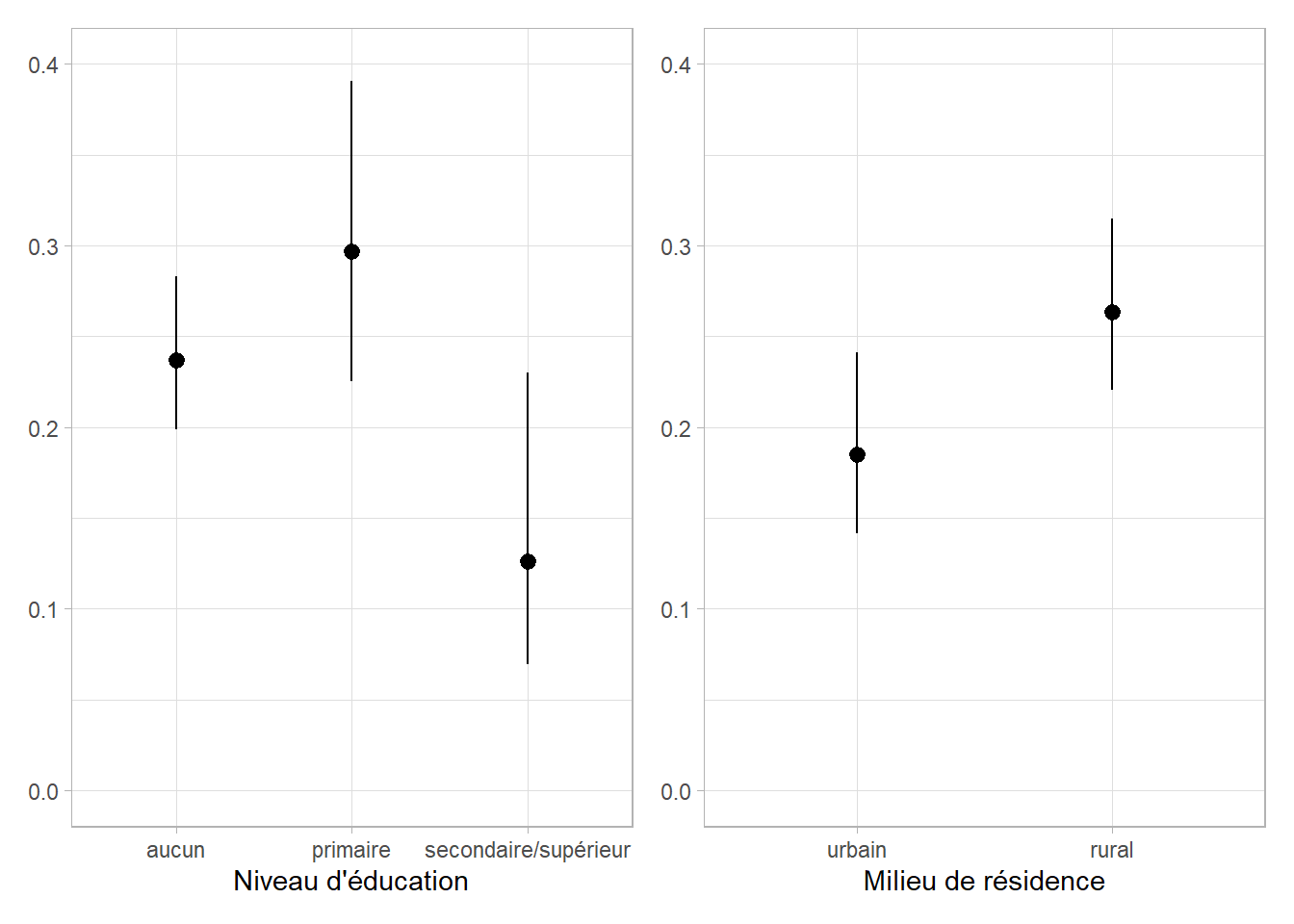
Nous pouvons vérifier visuellement ce résultat en réalisant un graphique des prédictions marginales moyennes avec broom.helpers::plot_marginal_predictions() (cf. Section 24.3).

broom.helpers::plot_marginal_predictions(mod1_poisson) |> 
  patchwork::wrap_plots() &
  ggplot2::scale_y_continuous(limits = c(0, .4))
Figure 43.2: Prédictions marginales du modèle de Poisson

43.1.3 Évaluation de la surdispersion

Comme tous les modèles GLM, le modèle de Poisson présuppose que les observations sont indépendantes les unes des autres2. Surtout, la distribution de Poisson présuppose que la variance est égale à la moyenne. Or, il arrive fréquemment que la variance soit supérieure à la moyenne, auquel cas on parle alors de surdispersion. Si c’est le cas, le modèle de Poisson va sous-estimer la variance et produire des intervalles de confiance trop petit et des p-valeurs trop petites.

2 Si ce n’était pas le cas, par exemple s’il y a plusieurs observations pour un même individu, il faudrait adopter un autre type de modèle, par exemple un modèle mixte ou un modèle GEE, pour lesquels il est possible d’utiliser une distribution de Poisson.

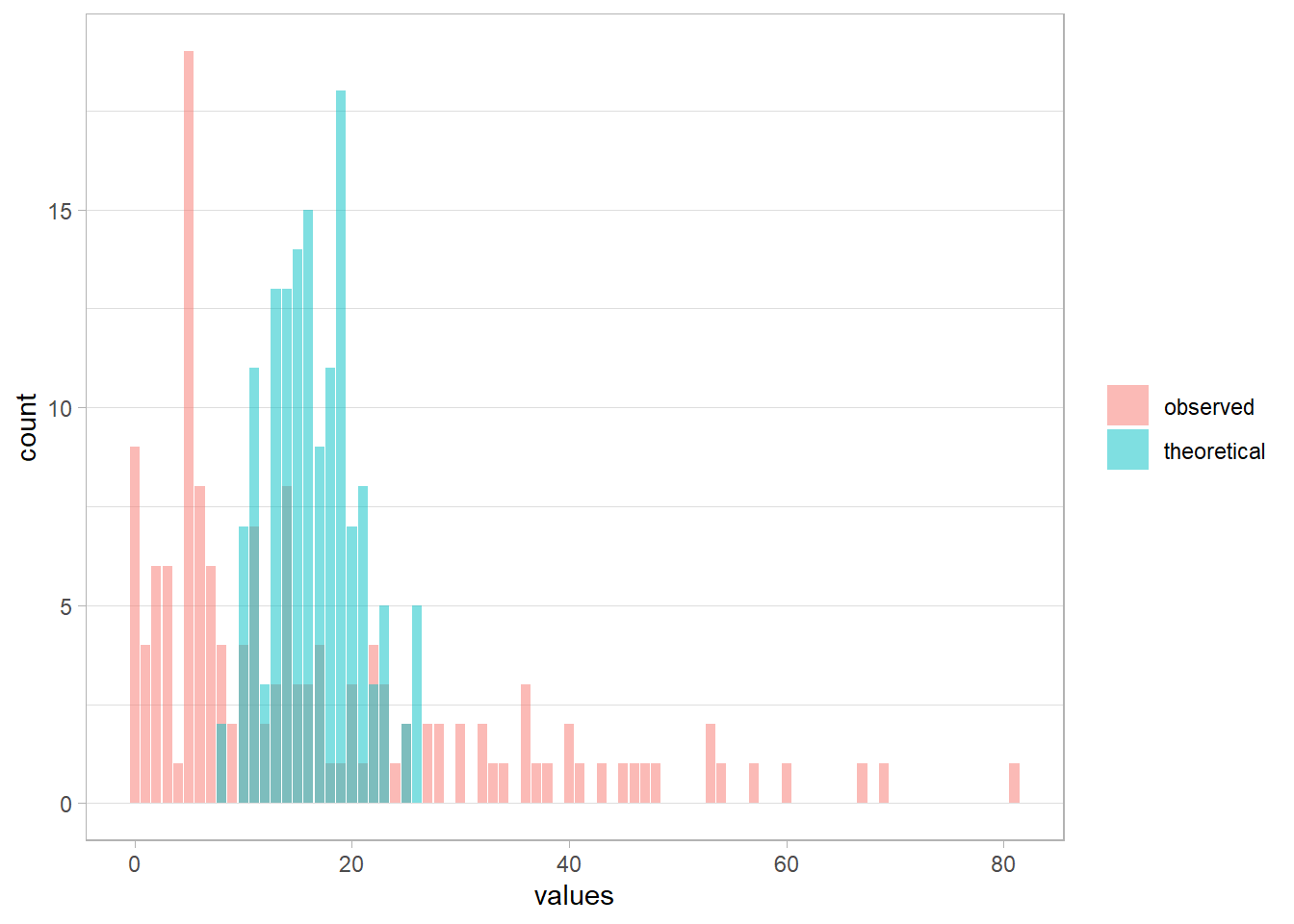
En premier lieu, nous pouvons vérifier si la distribution observée des données correspond peu ou prou à la distribution théorique de Poisson pour une moyenne correspondant à la moyenne observée.

La fonction ci-dessous permet justement de comparer la distribution observée avec la distribution théorique d’un modèle.

observed_vs_theoretical <- function(model) {
  observed <- model.response(model.frame(model))
  theoretical <- simulate(model, nsim = 1)
  theoretical <- theoretical[[1]]
  df <- dplyr::tibble(
    status = c(
      rep.int("observed", length(observed)),
      rep.int("theoretical", length(theoretical))
    ),
    values = c(observed, theoretical)
  )
  if (is.numeric(observed) && any(observed != as.integer(observed))) {
    ggplot2::ggplot(df) +
    ggplot2::aes(x = values, fill = status) +
    ggplot2::geom_density(
      alpha = .5,
      position = "identity"
    ) +
    ggplot2::theme_light() +
    ggplot2::labs(fill = NULL)
  } else {
    ggplot2::ggplot(df) +
    ggplot2::aes(x = values, fill = status) +
    ggplot2::geom_bar(
      alpha = .5,
      position = "identity"
    ) +
    ggplot2::theme_light() +
    ggplot2::theme(
      panel.grid.major.x = ggplot2::element_blank(),
      panel.grid.minor.x = ggplot2::element_blank()
    ) +
    ggplot2::labs(fill = NULL)
  }
}

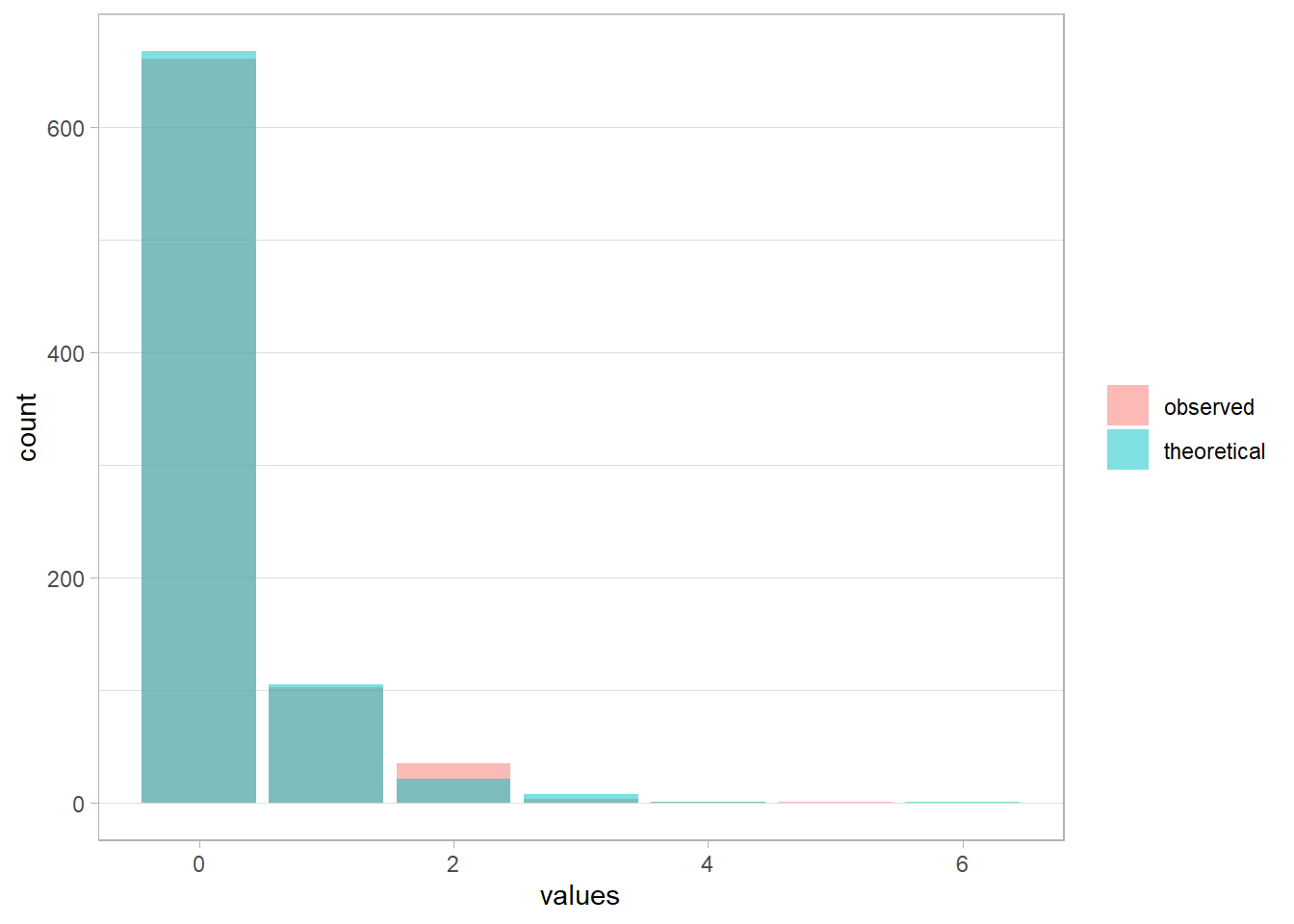
Appliquons cette fonction à notre modèle de Poisson.

mod1_poisson |> 
  observed_vs_theoretical()
Figure 43.3: Distribution observée vs distribution théorique de la descendance atteinte à 30 ans (modèle de Poisson)

Les deux distributions restent assez proches même si la distribution observée est légèrement décalée vers la droite.

Note

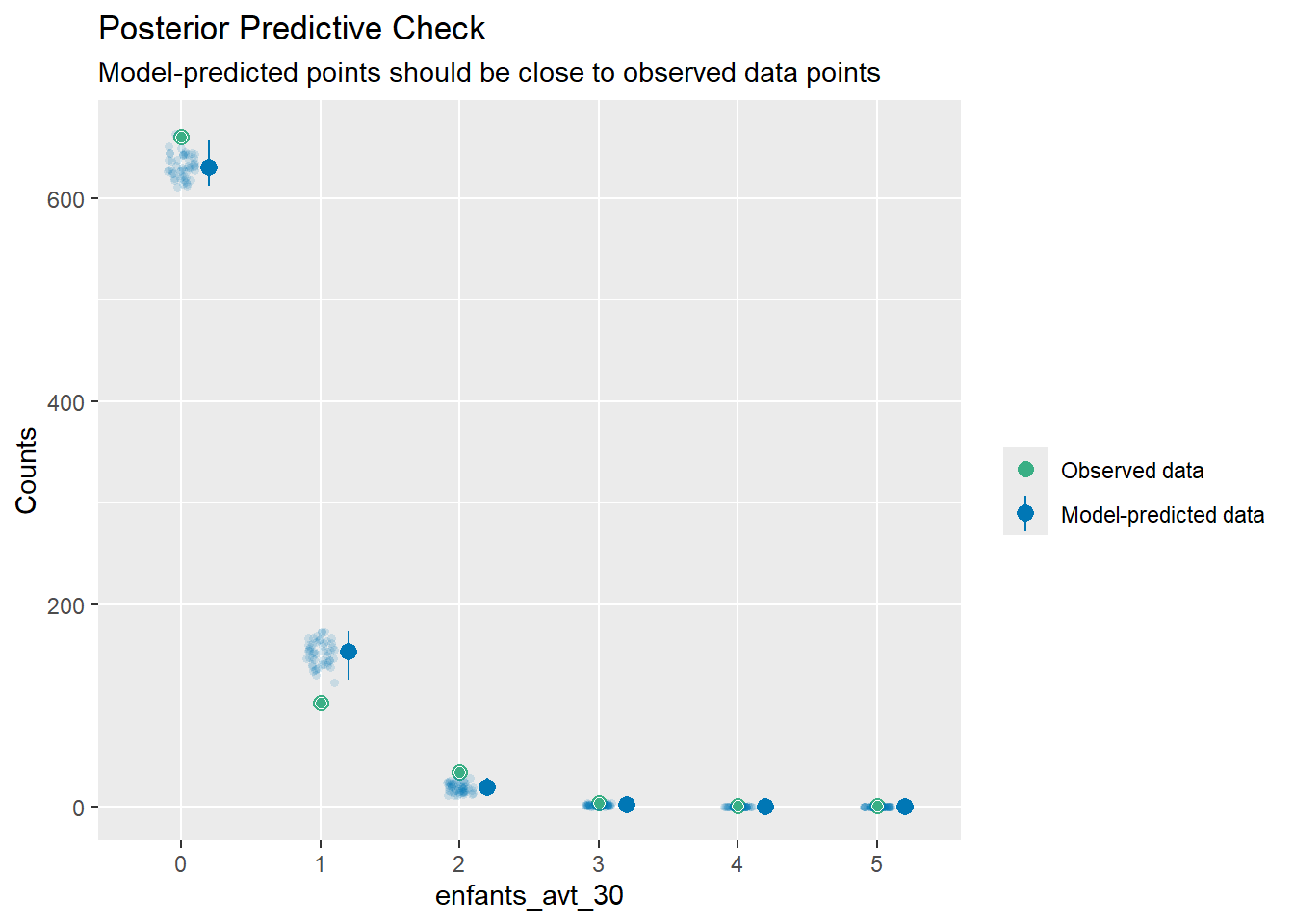
La fonction performance::check_predictions() propose une visualisation un peu plus avancée.

mod1_poisson |>
  performance::check_predictions(type = "discrete_both")
Warning: Maximum value of original data is not included in the
  replicated data.
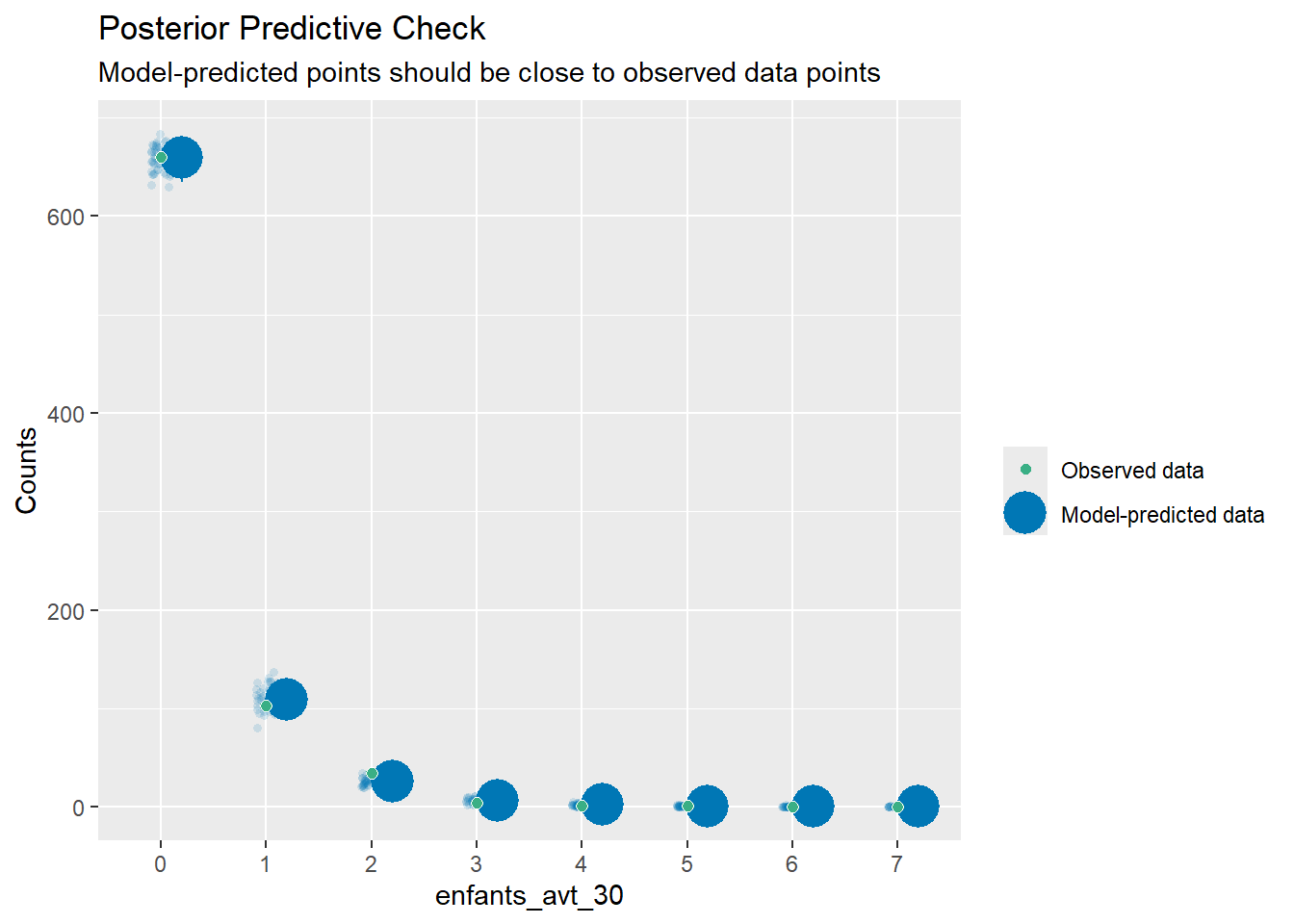
  Model may not capture the variation of the data.

Les points verts correspondent au nombre d’individus observés (sur l’axe vertical) pour chaque valeur de notre variable à expliquer (sur l’axe horizontal). La fonction simule ensuite une cinquantaine de jeu de données par réplication et affiche les prédictions du modèle pour ces jeux de données (points bleus avec effet de transparence), ainsi que les prédictions médianes (point bleu sans transparence) et l’intervalle des prédictions (barres verticales).

Dans notre exemple, on voit notamment que le modèle a du mal à prédire correctement le nombre d’individus avec 0, 1 ou 2 enfants.

Le paramètre φ (phi) qui correspond au ratio entre la variance observée et la variance théorique peut être estimée, en pratique, selon certains auteurs, comme le ratio de la déviance résiduelle sur le nombre de degrés de libertés du modèle. Il s’obtient ainsi :

mod1_poisson$deviance / mod1_poisson$df.residual
[1] 0.8580717

Si ce ratio s’écarte de 1, alors il y a un problème de surdispersion. Cependant, en pratique, il n’y a pas de seuil précis à partir duquel nous pourrions conclure qu’il faut rejeter le modèle.

La package {AER} propose un test, AER::dispersiontest(), pour tester s’il y a un problème de surdispersion. Ce test ne peut s’appliquer qu’à un modèle de Poisson.

mod1_poisson |> AER::dispersiontest()

    Overdispersion test

data:  mod1_poisson
z = 3.3367, p-value = 0.0004238
alternative hypothesis: true dispersion is greater than 1
sample estimates:
dispersion 
  1.361364

Le package performance propose, quant à lui, un test plus générale de surdispersion via la fonction performance::check_overdispersion().

mod1_poisson |> 
  performance::check_overdispersion()
# Overdispersion test

       dispersion ratio =    1.371
  Pearson's Chi-Squared = 1096.575
                p-value =  < 0.001
Overdispersion detected.

Dans les deux cas, nous obtenons une p-valeur inférieure à 0,001, indiquant que le modèle de Poisson n’est peut-être pas approprié ici.

43.2 Modèle de quasi-Poisson

Le modèle de quasi-Poisson est similaire au modèle de Poisson mais autorise plus de souplesse pour la modélisation de la variance qui est alors modélisée comme une relation linéaire de la moyenne. Il se calcule également avec stats::glm(), mais en indiquant family = quasipoisson. Comme avec le modèle de Poisson, la fonction de lien par défaut est la fonction logarithmique (log).

mod1_quasi <- glm(
  enfants_avt_30 ~ educ2 + milieu,
  family = quasipoisson,
  data = femmes30p
)
Important

L’AIC (Akaike information criterion) n’est pas défini pour ce type de modèle. Il n’est donc pas possible d’utiliser stats::step() avec un modèle de quasi-Poisson. Si l’on veut procéder à une sélection pas à pas descendante, on procédera donc en amont avec un modèle de Poisson classique.

Regardons les résultats obtenus :

mod1_quasi |> 
  tbl_regression(exponentiate = TRUE) |> 
  bold_labels()
Caractéristique IRR1 95% IC1 p-valeur
Niveau d'éducation


    aucun — —
    primaire 1,25 0,85 – 1,81 0,2
    secondaire/supérieur 0,53 0,23 – 1,05 0,10
Milieu de résidence


    urbain — —
    rural 1,42 0,99 – 2,10 0,067
1 IRR = rapport de taux d’incidence, IC = intervalle de confiance
Table 43.2: Tableau des coefficients du modèle de quasi-Poisson

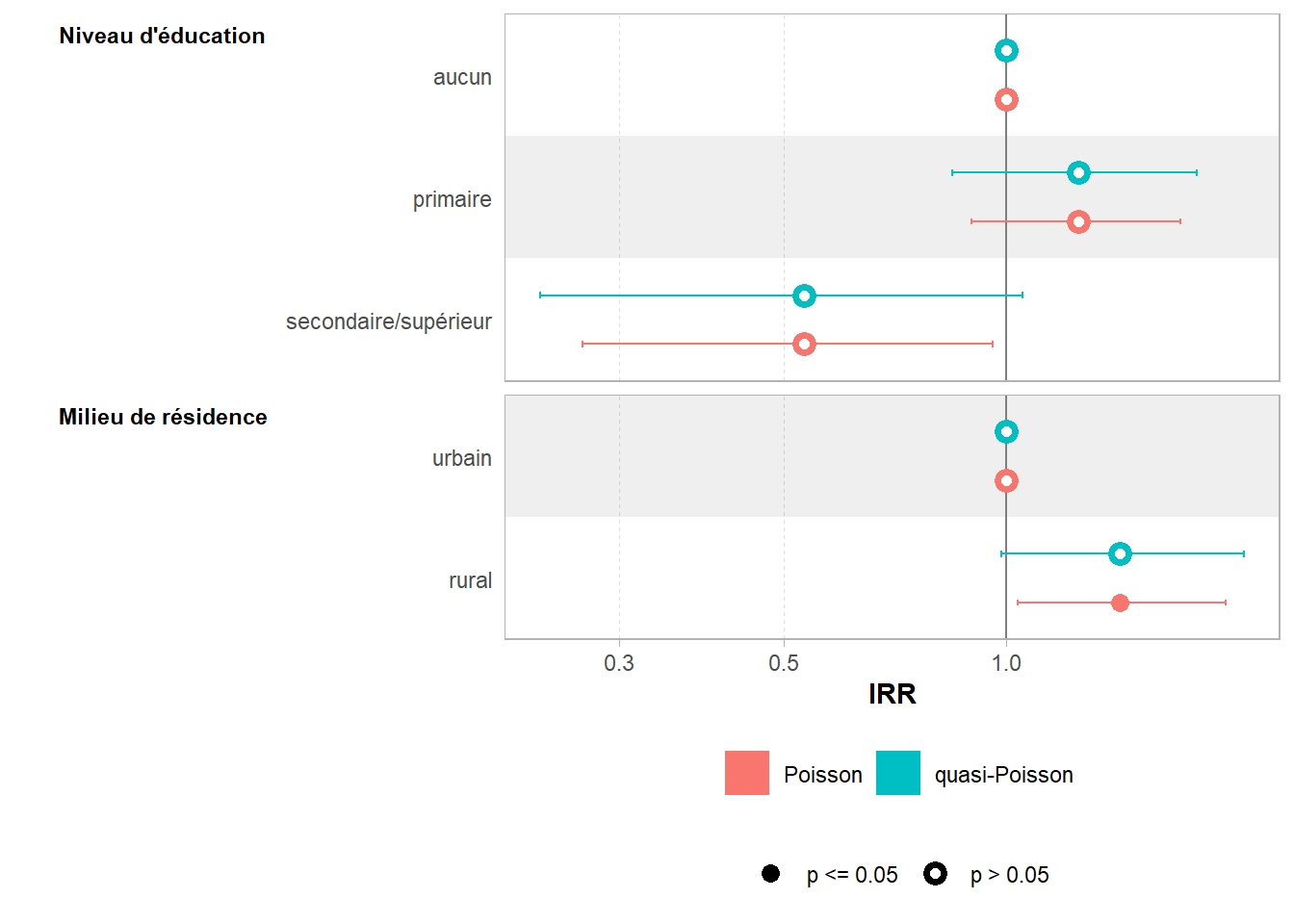
Les coefficients sont identiques à ceux obtenus avec le modèle de Poisson (cf. Table 43.1), mais les intervalles de confiance sont plus larges et les p-valeurs plus élevées, traduisant la prise en compte d’une variance plus importante. Cela se voit aisément si l’on compare les coefficients avec ggstats::ggcoef_compare().

list(Poisson = mod1_poisson, "quasi-Poisson" = mod1_quasi) |>
  ggcoef_compare(exponentiate = TRUE)
Figure 43.4: Comparaison des coefficients du modèle de Poisson et du modèle de quasi-Poisson

Le passage à un modèle de quasi-Poisson aura-t-il été suffisant pour régler notre problème de surdispersion ? La fonction performance::check_overdispersion() peut être appliquée à un modèle de quasi-Poisson.

mod1_quasi |> 
  performance::check_overdispersion()
# Overdispersion test

       dispersion ratio =    1.371
  Pearson's Chi-Squared = 1096.575
                p-value =  < 0.001
Overdispersion detected.

Il semble que nous ayons toujours une surdispersion, insuffisamment corrigée par le modèle de quasi-Poisson.

43.3 Modèle binomial négatif

Le modèle binomial négatif (negative binomial en anglais) modélise la variance selon une spécification quadratique (i.e. selon le carré de la moyenne). Il est implémenté dans le package MASS via la fonction MASS::glm.nb(). Les autres paramètres sont identiques à ceux de stats::glm().

mod1_nb <- MASS::glm.nb(
  enfants_avt_30 ~ educ2 + milieu + region,
  data = femmes30p
)

L’AIC étant défini pour pour ce type de modèle, nous pouvons procéder à une sélection pas à pas avec stats::step().

mod1_nb <- mod1_nb |> step()
Start:  AIC=979.1
enfants_avt_30 ~ educ2 + milieu + region

         Df Deviance    AIC
- region  3   462.89 975.01
<none>        460.98 979.10
- milieu  1   463.29 979.41
- educ2   2   466.11 980.22

Step:  AIC=975
enfants_avt_30 ~ educ2 + milieu

         Df Deviance    AIC
<none>        460.14 975.00
- milieu  1   463.37 976.24
- educ2   2   465.54 976.40

La fonction de lien étant toujours logarithmique, nous pouvons donc afficher plutôt l’exponentielle des coefficients qui s’interprètent comme pour un modèle de Poisson.

mod1_nb |> 
  tbl_regression(exponentiate = TRUE) |> 
  bold_labels()
Caractéristique IRR1 95% IC1 p-valeur
Niveau d'éducation


    aucun — —
    primaire 1,23 0,82 – 1,82 0,3
    secondaire/supérieur 0,53 0,25 – 1,03 0,074
Milieu de résidence


    urbain — —
    rural 1,41 0,97 – 2,06 0,076
1 IRR = rapport de taux d’incidence, IC = intervalle de confiance
Table 43.3: Tableau des coefficients du modèle binomial négatif

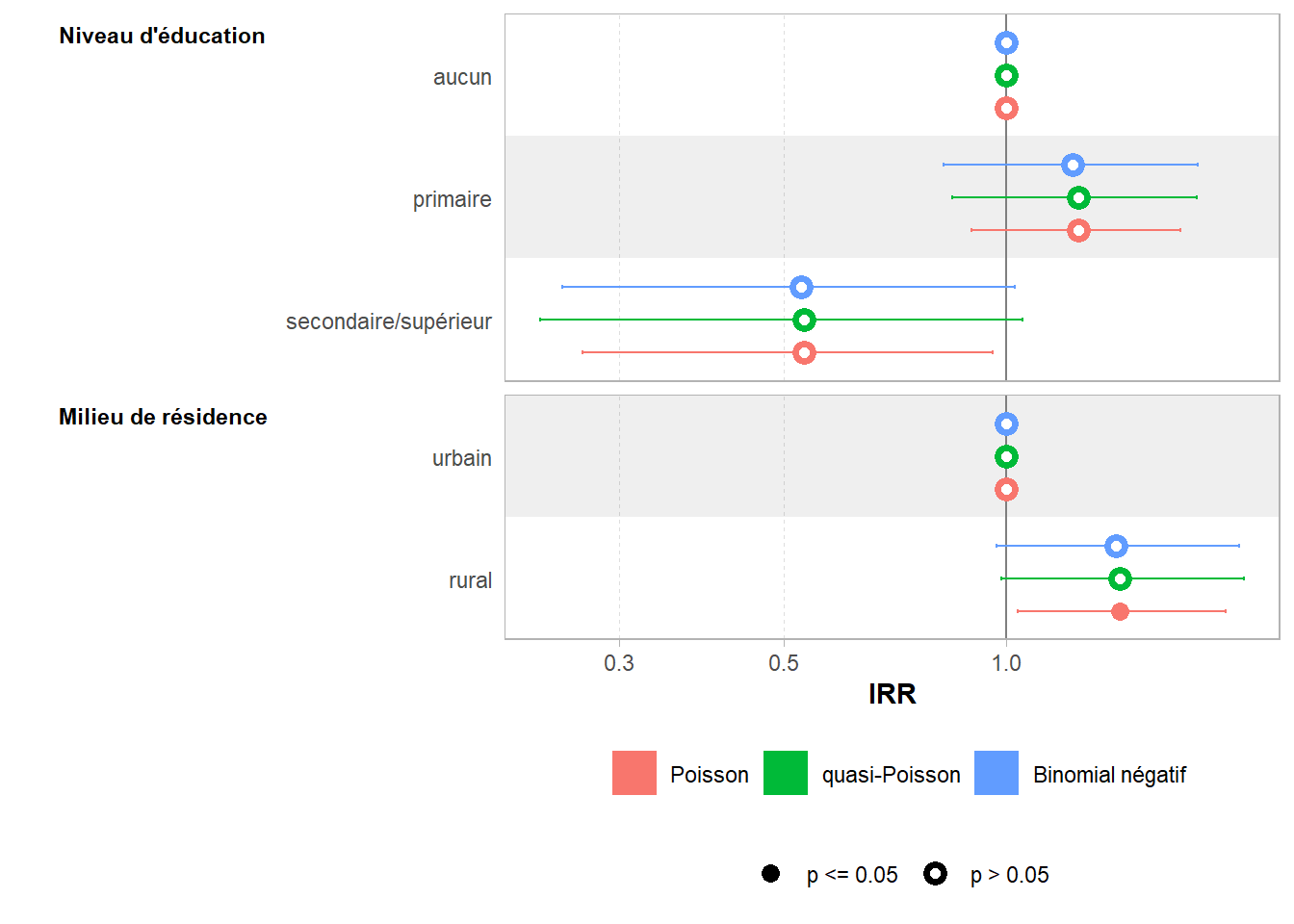
Cette fois-ci, les coefficients sont légèrement différents par rapport au modèle de Poisson, ce qui se voit aisément si l’on compare les trois modèles.

list(
  Poisson = mod1_poisson,
  "quasi-Poisson" = mod1_quasi,
  "Binomial négatif" = mod1_nb
) |>
  ggcoef_compare(exponentiate = TRUE)
Figure 43.5: Comparaison des coefficients du modèle de Poisson, du modèle de quasi-Poisson et du modèle binomial négatif

Nous pouvons comparer la distribution observée et la distribution théorique et constater que les prédictions sont plus proches des données observées.

mod1_nb |>
  observed_vs_theoretical()
mod1_nb |>
  performance::check_predictions(type = "discrete_both")
Figure 43.6: Distribution observée vs distribution théorique de la descendance atteinte à 30 ans (modèle négatif binomial)
Figure 43.7: Distribution observée vs distribution théorique de la descendance atteinte à 30 ans (modèle négatif binomial)

Nous pouvons vérifier la surdispersion.

mod1_nb |> 
  performance::check_overdispersion()
# Overdispersion test

 dispersion ratio = 0.975
          p-value = 0.856
No overdispersion detected.

Ouf ! Nous n’avons plus de problème de surdispersion.

Pour celles et ceux intéressé·es, il est possible de comparer la performance des modèles avec la fonction performance::compare_performance().

performance::compare_performance(
  mod1_poisson,
  mod1_nb,
  metrics = "common"
)
# Comparison of Model Performance Indices

Name         |  Model |  AIC (weights) |  BIC (weights) | Nagelkerke's R2 |  RMSE
---------------------------------------------------------------------------------
mod1_poisson |    glm | 1010.7 (<.001) | 1029.4 (<.001) |           0.033 | 0.579
mod1_nb      | negbin |  977.0 (>.999) | 1000.5 (>.999) |           0.032 | 0.579

43.4 Exemple avec une plus grande surdispersion

Pour ce second exemple, nous allons considérer le jeu de données MASS::quine qui contient les données de 146 enfants scolarisés en Australie, notamment le nombre de jours d’absence à l’école au cours de l’année passée, le sexe l’enfant et leur vitesse d’apprentissage (dans la moyenne ou lentement).

Préparons les données en francisant les facteurs et en ajoutant des étiquettes de variable.

d <- MASS::quine |>
  mutate(
    jours = Days,
    sexe = Sex |>
      fct_recode(
        "fille" = "F",
        "garçon" = "M"
      ),
    apprentissage = Lrn |>
      fct_recode(
        "dans la moyenne" = "AL",
        "lentement" = "SL"
      )
  ) |>
  set_variable_labels(
    jours = "Nombre de jours d'absence à l'école",
    sexe = "Sexe de l'enfant",
    apprentissage = "Vitesse d'apprentissage"
  )

Calculons notre modèle de Poisson.

mod2_poisson <- glm(
  jours ~ sexe + apprentissage,
  data = d,
  family = poisson
)

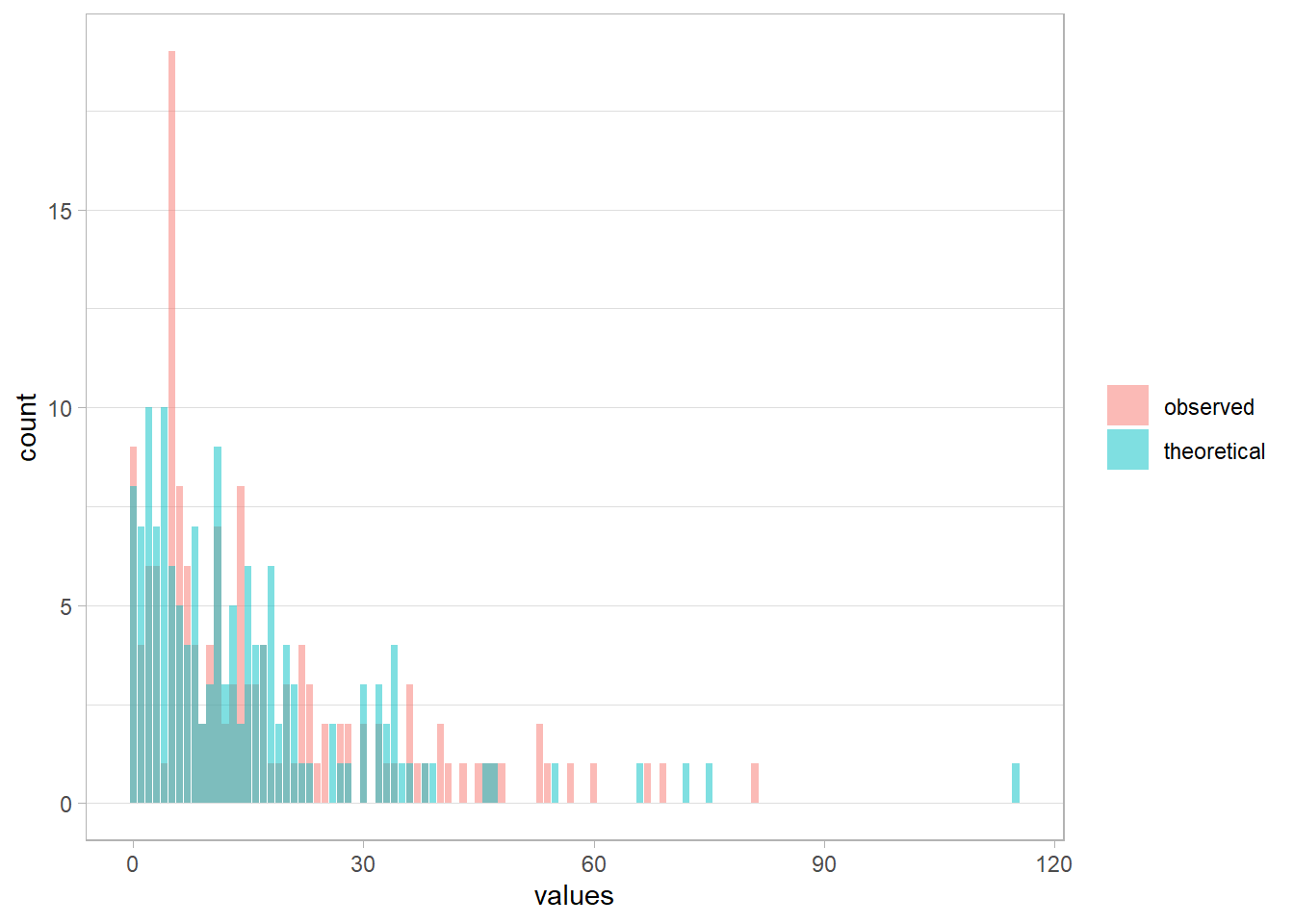
Comparons les données observées avec les données prédites.

mod2_poisson |> 
  observed_vs_theoretical()
Figure 43.8: Distribution observée vs distribution théorique du nombre de jours d’absence (modèle de Poisson)

Nous voyons très clairement un décalage des deux distributions. Notre modèle de Poisson n’arrive pas à capturer la variabilité des observations. Faisons le test de surdispersion pour vérifier.

mod2_poisson |> 
  performance::check_overdispersion()
# Overdispersion test

       dispersion ratio =   15.895
  Pearson's Chi-Squared = 2273.046
                p-value =  < 0.001
Overdispersion detected.

Calculons un modèle binomial négatif et voyons si cela améliore la situation.

mod2_nb <- MASS::glm.nb(
  jours ~ sexe + apprentissage,
  data = d
)
mod2_nb |> 
  observed_vs_theoretical()
Figure 43.9: Distribution observée vs distribution théorique du nombre de jours d’absence (modèle binomial négatif)

Les deux distributions sont bien plus proches maintenant. Vérifions la surdispersion.

mod2_nb |> 
  performance::check_overdispersion()
# Overdispersion test

 dispersion ratio = 0.978
          p-value = 0.992
No overdispersion detected.

Voilà !

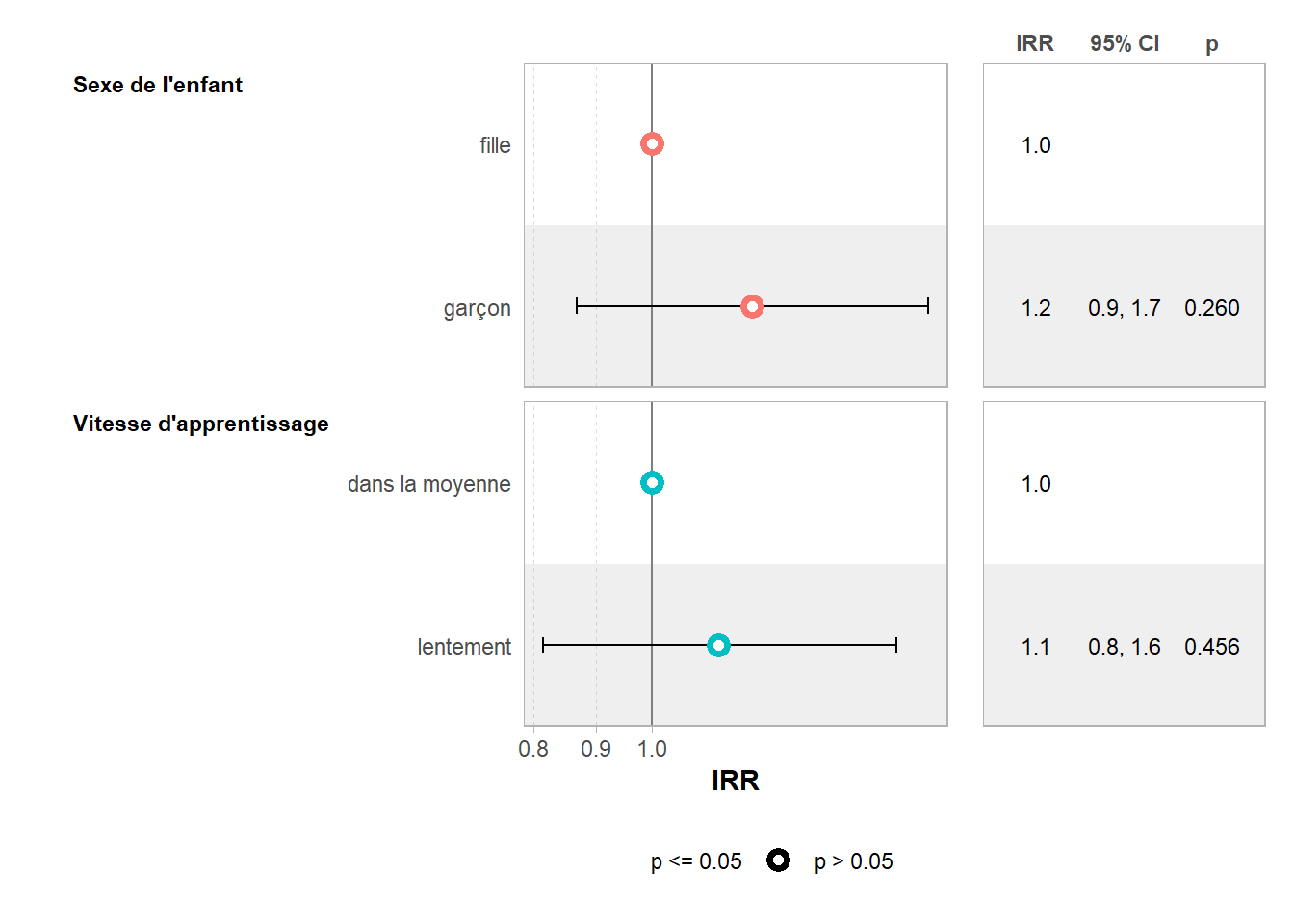
Pour finir, visualisons les coefficients du modèle.

mod2_nb |> 
  ggcoef_table(exponentiate = TRUE)
Figure 43.10: Facteurs associés à l’absentéisme scolaire (modèle négatif binomial)

43.5 Modèles de comptage avec une variable binaire

Pour l’analyse d’une variable binaire, les modèles de comptage représentent une alternative à la régression logistique binaire (cf. Chapitre 22). L’intérêt est de pouvoir interpréter les coefficients comme des prevalence ratio plutôt que des odds ratio.

Reprenons un exemple, que nous avons déjà utilisé à plusieurs reprises, concernant la probabilité de faire du sport, à partir de l’enquête histoires de vie 2003. Commençons par charger et recoder les données.

data(hdv2003, package = "questionr")

d <-
  hdv2003 |> 
  mutate(
    groupe_ages = age |>
      cut(
        c(18, 25, 45, 65, 99),
        right = FALSE,
        include.lowest = TRUE,
        labels = c("18-24 ans", "25-44 ans",
                   "45-64 ans", "65 ans et plus")
      )
  ) |> 
  set_variable_labels(
    sport = "Pratique un sport ?",
    sexe = "Sexe",
    groupe_ages = "Groupe d'âges",
    heures.tv = "Heures de télévision / jour"
  )

Pour la variable sexe, nous allons définir la modalité Femme comme modalité de référence. Pour cela, nous allons utiliser un contraste personnalisé (cf. Chapitre 25).

levels(d$sexe)
[1] "Homme" "Femme"
contrasts(d$sexe) <- contr.treatment(2, base = 2)

Calculons le modèle de régression logistique binaire classique.

mod3_binomial <- glm(
  sport ~ sexe + groupe_ages + heures.tv,
  family = binomial,
  data = d
)

Nous allons maintenant calculer un modèle de Poisson. Nous devons déjà ré-exprimer notre variable à expliquer sous la forme d’une variable numérique égale à 0 si l’on ne pratique pas de sport et à 1 si l’on pratique un sport.

levels(d$sport)
[1] "Non" "Oui"
d$sport2 <- as.integer(d$sport == "Oui")
mod3_poisson <- glm(
  sport2 ~ sexe + groupe_ages + heures.tv,
  family = poisson,
  data = d
)

Vérifions si nous avons un problème de surdispersion.

performance::check_overdispersion(mod3_poisson)
# Overdispersion test

       dispersion ratio =    0.635
  Pearson's Chi-Squared = 1263.552
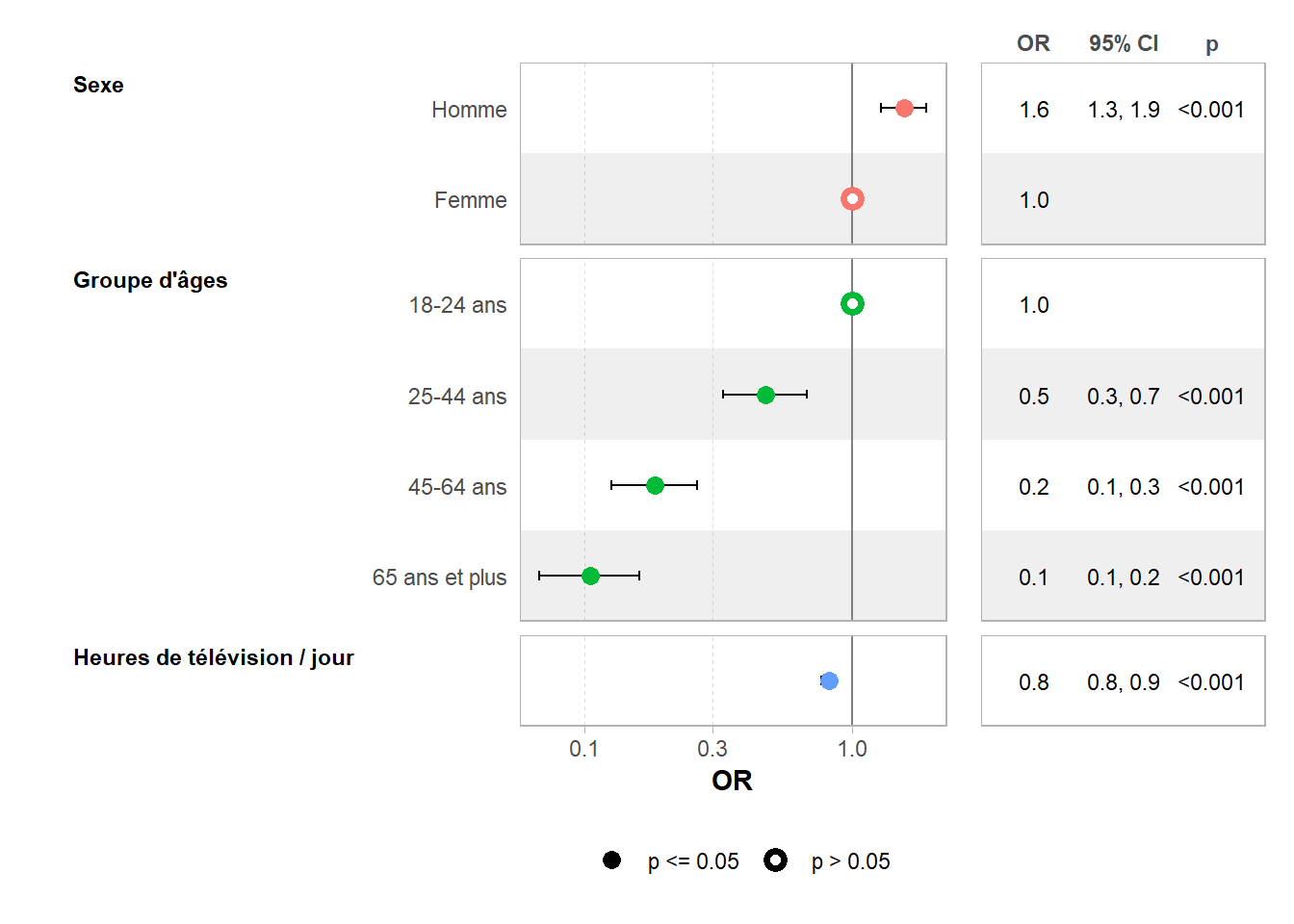
                p-value =        1
No overdispersion detected.

Regardons maintenant les résultats de nos deux modèles.

mod3_binomial |> 
  ggstats::ggcoef_table(exponentiate = TRUE)
Figure 43.11: Facteurs associés à la pratique d’un sport (régression logistique) 
mod3_poisson |> 
  ggstats::ggcoef_table(exponentiate = TRUE)
Figure 43.12: Facteurs associés à la pratique d’un sport (régression de Poisson)

Nous pouvons voir ici que les deux modèles fournissent des résultats assez proches. Par contre, les coefficients ne s’interprètent pas de la même manière. Dans le cadre de la régression logistique, il s’agit d’odds ratios (ou rapports des côtes) définis comme \(OR_{A/B}=(\frac{p_A}{1-p_A})/(\frac{p_B}{1-p_B})\) où \(p_A\) correspond à la probabilité de faire du sport pour la modalité \(A\). Pour la régression de Poisson, il s’agit de prevalence ratios (rapports des prévalences) définis comme \(PR_{A/B}=p_A/p_B\). Avec un rapport des prévalences de 1,3, nous pouvons donc dire que, selon le modèle, les hommes ont 30% de chance en plus de pratiquer un sport.

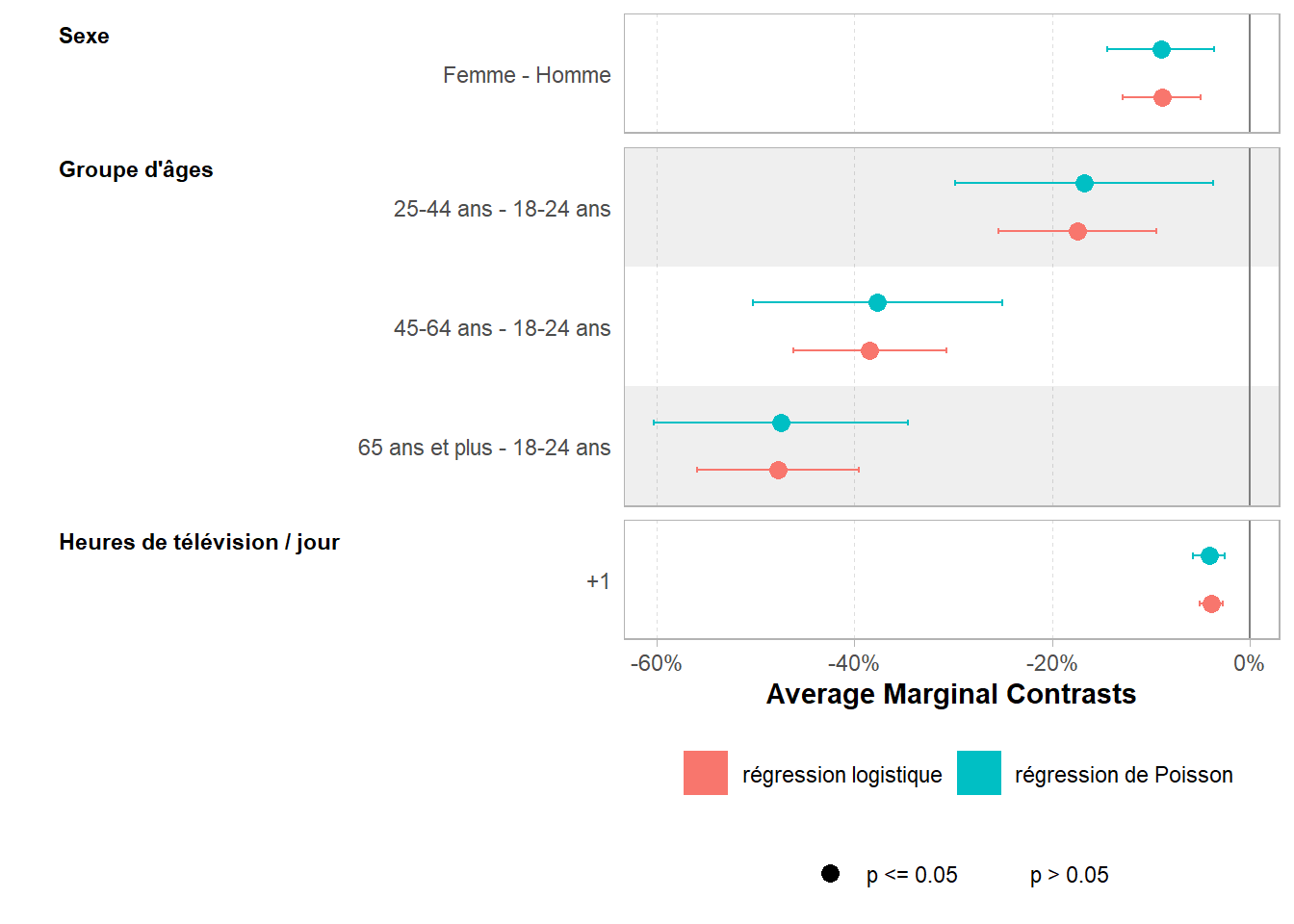
Pour mieux comparer les deux modèles, nous pouvons présenter les résultats sous la forme de contrastes marginaux moyens (cf. Section 24.4) qui, pour rappel, sont exprimés dans l’échelle de la variable d’intérêt, soit ici sous la forme d’une différence de probabilité.

list(
  "régression logistique" = mod3_binomial,
  "régression de Poisson" = mod3_poisson
) |> 
  ggcoef_compare(tidy_fun = broom.helpers::tidy_marginal_contrasts) +
  scale_x_continuous(labels = scales::percent)
Figure 43.13: Comparaison des contrastes marginaux des deux modèles

Les résultats sont ici très proches. Nous pouvons néanmoins constater que les intervalles de confiance pour la régression de Poisson sont un peu plus large. Nous pouvons comparer les deux modèles avec performance::compare_performance() pour constater que, dans notre exemple, la régression de Poisson est un peu moins bien ajustée aux données que la régression logistique binaire. Cependant, en pratique, cela n’est pas ici problématique : le choix entre les deux modèles peut donc se faire en fonction de la manière dont on souhaite présenter et narrer les résultats.

performance::compare_performance(
  mod3_binomial,
  mod3_poisson,
  metrics = "common"
)
Warning: contrasts dropped from factor sexe
Warning: contrasts dropped from factor sexe
Warning: contrasts dropped from factor sexe
Warning: contrasts dropped from factor sexe
# Comparison of Model Performance Indices

Name          | Model |  AIC (weights) |  BIC (weights) |  RMSE | Tjur's R2 | Nagelkerke's R2
---------------------------------------------------------------------------------------------
mod3_binomial |   glm | 2346.3 (>.999) | 2379.8 (>.999) | 0.447 |     0.132 |                
mod3_poisson  |   glm | 2748.8 (<.001) | 2782.4 (<.001) | 0.447 |           |           0.158
Astuce

Lorsque l’on a une variable binaire à expliquer et que l’on souhaite calculer des risques relatifs (RR) ou prevalence ratio (PR), une alternative au modèle de Poisson est le modèle log-binomial. Il s’agit d’un modèle binomial avec une fonction de lien logarithme.

Il faut noter que ce type de modèles a parfois du mal à converger.

mod3_log <- glm(
  sport ~ sexe + groupe_ages + heures.tv,
  family = binomial(link = "log"),
  data = d
)
Error: impossible de trouver un jeu de coefficients correct : prière de fournir des valeurs initiales

C’est le cas ici ! Nous allons donc initier le modèle avec les coefficients du modèle de Poisson.

mod3_log <- glm(
  sport ~ sexe + groupe_ages + heures.tv,
  family = binomial(link = "log"),
  start = mod3_poisson$coefficients,
  data = d
)

Regardons les résultats.

mod3_log |>
  ggstats::ggcoef_table(exponentiate = TRUE)
Warning: le pas a été tronqué à cause de la divergence
Warning: le pas a été tronqué à cause de la divergence
Warning: glm.fit: l'algorithme n'a pas convergé
Warning: glm.fit: l'algorithme n'a pas convergé
Warning: le pas a été tronqué à cause de la divergence
Warning: glm.fit: l'algorithme n'a pas convergé

Nous obtenons des résultats assez proches de ceux du modèle de Poisson. Notons cependant les différents avis affichés qui nous indiquent que le modèle a eu des difficultés à converger3.

Le package logbin propose, via login::logbin(), une implémentation de la régression log-binomiale en proposant des algorithmes de convergence plus stables.

mod3_logbin <- logbin::logbin(
  sport ~ sexe + groupe_ages + heures.tv,
  data = d
)

Les résultats sont très proches.

mod3_logbin |>
  ggstats::ggcoef_table(exponentiate = TRUE)
Warning: The `tidy()` method for objects of class `logbin` is not maintained by the broom team, and is only supported through the `glm` tidier method. Please be cautious in interpreting and reporting broom output.

This warning is displayed once per session.

3 Sur ce sujet, on pourra consulter l’article Log-binomial models: exploring failed convergence par Tyler Williamson, Misha Eliasziw et Gordon Hilton Fick, DOI: 10.1186/1742-7622-10-14. On pourra également consulter cet échange sur StackExchange.

43.6 Données pondérées et plan d’échantillonnage

Lorsque l’on a des données pondérées avec prise en compte d’un plan d’échantillonnage (cf. Chapitre 28), on ne peut utiliser directement stats::glm() avec un objet survey. On aura alors recours à survey::svyglm() qui est très similaire.

library(srvyr)
library(survey)
dp <- d |> 
  as_survey_design(weights = poids)
mod4_poisson <- svyglm(
  sport2 ~ sexe + groupe_ages + heures.tv,
  family = poisson,
  design = dp
)
mod4_quasi <- svyglm(
  sport2 ~ sexe + groupe_ages + heures.tv,
  family = quasipoisson,
  design = dp
)

Il est tout à fait possible d’appliquer stats::step() à ces modèles4.

4 Y compris, dans le cas présent, au modèle de quasi-Poisson.

Concernant la régression binomiale négative, il n’y a pas d’implémentation fournie directement par survey. Cependant, le package sjstats en propose une via la fonction sjstats::svyglm.nb().

mod4_nb <- sjstats::svyglm.nb(
  sport2 ~ sexe + groupe_ages + heures.tv,
  design = dp
)
Warning in theta.ml(Y, mu, sum(w), w, limit = control$maxit, trace =
control$trace > : nombre limite d'iterations atteint
Warning in theta.ml(Y, mu, sum(w), w, limit = control$maxit, trace =
control$trace > : nombre limite d'iterations atteint
Note

Une alternative possible consiste à utiliser des poids de réplication selon une approche du type bootsrap. Il faudra déjà définir des poids de réplication avec srvyr::as_survey_rep() puis avoir recours à survey::withReplicates(). Pour faciliter cette deuxième étape, on pourra se faciliter la vie avec le package svrepmisc et sa fonction svrepmisc::svynb(). Ce package n’étant pas disponible sur CRAN, on devra l’installer avec la commande remotes::install_github("carlganz/svrepmisc").

Attention : le temps de calcul du modèle avec les poids de réplication est de plusieurs minutes.

dp_rep <- dp |> 
  as_survey_rep(type = "bootstrap", replicates = 100)
mod4_nb_alt <- svrepmisc::svynb(
  sport2 ~ sexe + groupe_ages + heures.tv,
  design = dp_rep
)

43.7 Lectures complémentaires