── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.5
✔ forcats 1.0.0 ✔ stringr 1.5.1
✔ ggplot2 3.5.1 ✔ tibble 3.2.1
✔ lubridate 1.9.3 ✔ tidyr 1.3.1
✔ purrr 1.0.2
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors46 Modèles d’incidence / de taux
En épidémiologie, le taux d’incidence rapporte le nombre de nouveaux cas d’une pathologie observés pendant une période donnée à la population exposée pendant cette même période. En démographie, le terme de taux est utilisé pour désigner la fréquence relative d’un évènement au sein d’une population pendant une période de temps donnée (par exemple : taux de natalité).
Si l’ensemble des individus sont observés / exposés pendant une seule unité de temps (par exemple une année), alors cela revient à rapporter le nombre moyen d’évènements à 1 : nous pouvons utiliser un modèle classique de de comptage (cf. Chapitre 45).
Cependant, le plus souvent, la durée d’observation / d’exposition varie d’un individu à l’autre. Par exemple, si nous nous intéressons à un taux de divorce, les individus ne sont exposés au risque de divorcer qu’à partir du moment où ils sont mariés. De même, une fois divorcés ou veufs, ils ne sont plus exposés au risque de divorce (sauf s’ils se remarient ultérieurement). Pour chaque individu, il nous faut donc connaître le nombre d’évènements vécus (\(n_{evts}\)) et la durée d’exposition (\(d_{exp}\)). Ce que l’on cherche à modéliser est donc le ratio \(n_{evts}/d_{exp}\).
Une astuce consiste à modéliser ce taux à l’aide d’un modèle ayant une fonction de lien logarithmique (log) comme le modèle de Poisson ou le modèle binomial négatif. En effet, dans ce cas-là, on cherchera donc à modéliser notre variable sous la forme \(log(n_{evts}/d_{exp}) = \beta_iX_i\) où \(X_i\) représente les variables explicatives et \(\beta_i\) les coefficients du modèle. Or, \(log(n_{evts}/d_{exp}) = log(n_{evts}) - log(d_{exp})\). Nous pouvons donc réécrire l’équation du modèle sous la forme \(log(n_{evts}) = \beta_iX_i + log(d_{exp})\). Nous retombons sur un modèle de comptage classique, à condition d’ajouter à chaque observation ce qu’on appelle un décalage (offset en anglais) de \(log(d_{exp})\). Ce décalage correspond donc en quelque sorte à une variable ajoutée au modèle mais pour laquelle on ne calcule pas de coefficient.
46.1 Premier exemple (données individuelles, évènement unique)
Prenons un premier exemple à partir du jeux de données gtsummary::trial qui contient des informations sur 200 patients atteints d’un cancer. Il contient entre autre les variables suivantes :
death : variable binaire (0/1) indiquant si le patient est décédé
ttdeath : le nombre de mois d’observation jusqu’au décès (si décès) ou jusqu’à la fin de l’étude (si survie)
stage : un facteur indiquant le stade T de la tumeur (plus la valeur est élevée, plus la tumeur est grosse)
trt : le traitement reçu par le patient (A ou B)
response : une variable binaire (0/1) indiquant si le traitement a eu un effet sur la tumeur (diminution)
Nous nous intéressons donc aux facteurs associés au taux de mortalité (death/ttdeath) : nous allons donc réaliser un modèle de Poisson sur la variable death en ajoutant un décalage (offset) correspondant à log(ttdeath).
46.1.1 Statistiques descriptives
Pour réaliser un tableau des incidences, nous aurons recours à gtsummary::tbl_custom_summary() qui permets de réaliser des tableaux avancés avec des statistiques personnalisées. Nous allons utiliser cette fonction en combinaison avec gtsummary::ratio_summary() qui permet de calculer le ratio de deux variables ainsi que des intervalles de confiance à 95% via la fonction poisson.test(). Nous allons exprimer les taux d’incidence pour 100 personne-mois (pm, person-months en anglais).
N’oublions pas, en amont, de recoder la variable response en un facteur.
Attachement du package : 'gtsummary'L'objet suivant est masqué _par_ '.GlobalEnv':
trialpercent2 <- scales::label_percent(accuracy = .01, suffix = "")
trial |>
tbl_custom_summary(
include = c(stage, trt, response),
stat_fns = ~ ratio_summary("death", "ttdeath"),
statistic = ~"{ratio}/100pm [{conf.low} - {conf.high}] ({num}/{denom})",
digits = ~ c(percent2, percent2, percent2, 0, 0),
overall_row = TRUE,
overall_row_label = "Overall"
) |>
bold_labels()Characteristic |
N = 200 1 |
|---|---|
| Overall | 2.85/100pm [2.35 - 3.43] (112/3,925) |
| T Stage | |
| T1 | 2.17/100pm [1.39 - 3.23] (24/1,105) |
| T2 | 2.48/100pm [1.63 - 3.61] (27/1,089) |
| T3 | 2.58/100pm [1.62 - 3.91] (22/852) |
| T4 | 4.43/100pm [3.15 - 6.06] (39/879) |
| Chemotherapy Treatment | |
| Drug A | 2.62/100pm [1.96 - 3.44] (52/1,983) |
| Drug B | 3.09/100pm [2.36 - 3.98] (60/1,942) |
| Tumor Response | 1.85/100pm [1.19 - 2.76] (24/1,296) |
| Unknown | 7 |
|
1
ratio/100pm [conf.low - conf.high] (num/denom) |
|
Il n’existe pas de méthode add_p() utilisable ici. Nous verrons un peu plus loin (cf. Section 46.1.3) comment réaliser des modèles univariables qui permettront de calculer la relation de chaque prédicteur avec l’outcome avant ajustement.
46.1.2 Calcul et interprétation du modèle multivariable
Pour ajouter un décalage, nous avons deux syntaxes équivalentes : soit en ajoutant offset(log(ttdeath)) directement à l’équation du modèle, soit en passant à glm() l’argument offset = log(ttdeath).
Les deux écritures sont totalement équivalentes.
Vérifions la présence éventuelle de surdispersion.
# Overdispersion test
dispersion ratio = 0.850
Pearson's Chi-Squared = 159.039
p-value = 0.932No overdispersion detected.Tout est bon. Regardons maintenant les coefficients du modèle.
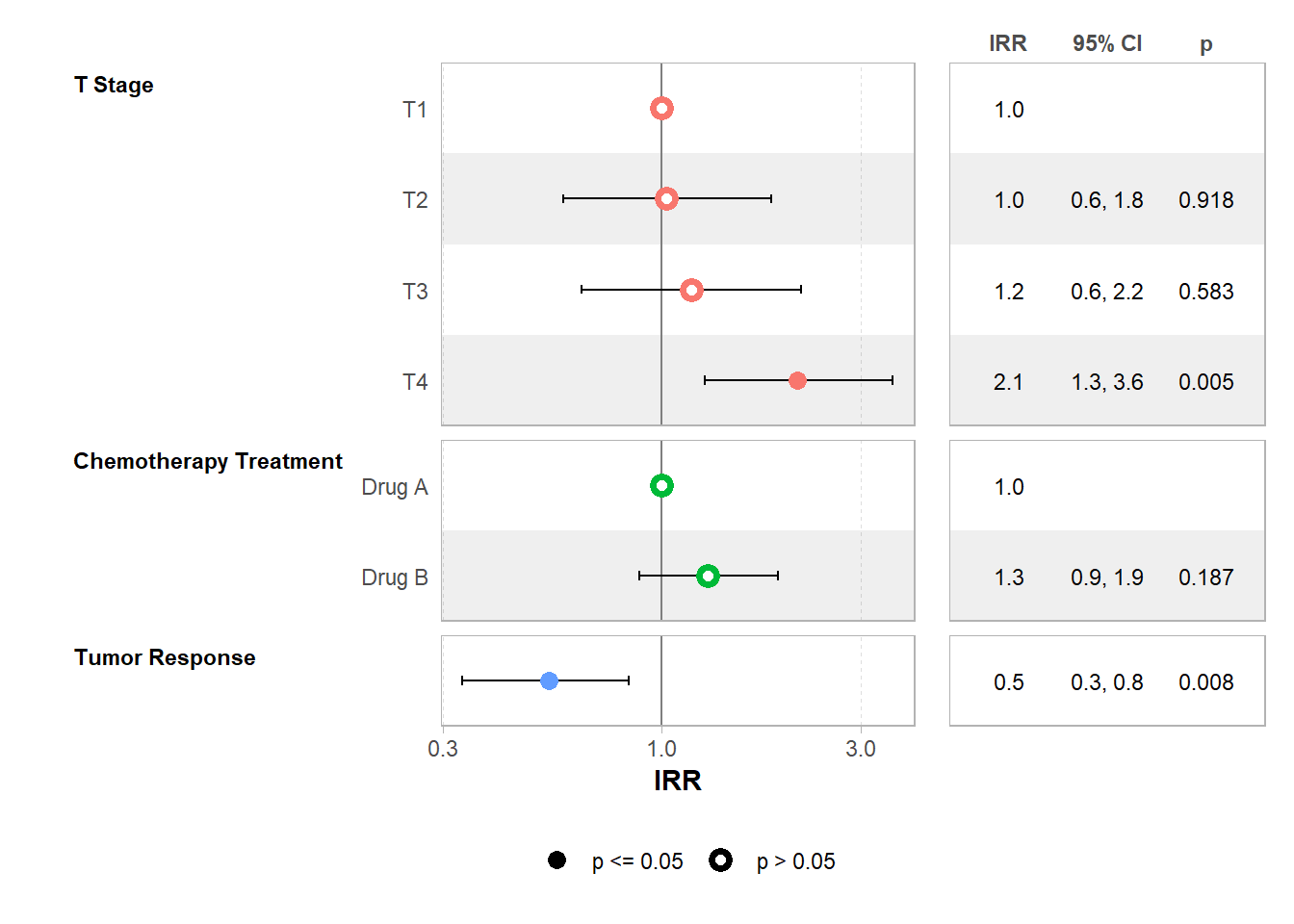
Nous avons affiché ici l’exponentielle des coefficients qui s’interprètent ici comme des IRR ou incidence rate ratio : le taux de décès est deux fois moindre pour les patients pour lesquels le traitement a eu un effet sur la tumeur (variable Tumor response). Sans surprise, le taux de décès est bien plus élevé selon la taille de la tumeur : 2,1 fois plus important pour ceux avec une tumeur au stade T4 par rapport à ceux ayant une tumeur au stade T1.
46.1.3 Modèles univariables
Pour tester les associations bivariées, nous pouvons avoir recours à des régressions univariables, que nous avons déjà abordé dans le chapitre sur la régression logistique binaire (cf. Section 22.9).
Pour cela, nous allons tout simplement appeler gtsummary::tbl_uvregression() avec gtsummary::add_global_p() pour obtenir des p-valeurs globales indiquant si chaque variable prédictive est associée à la mortalité (sans ajustement sur les autres variables).
trial |>
tbl_uvregression(
y = death,
include = c(stage, trt, response),
method = glm,
method.args = list(
family = poisson,
offset = log(ttdeath)
),
exponentiate = TRUE
) |>
add_global_p() |>
bold_labels()Characteristic |
N |
IRR 1 |
95% CI 1 |
p-value |
|---|---|---|---|---|
| T Stage | 200 | 0.025 | ||
| T1 | — | — | ||
| T2 | 1.14 | 0.66, 1.99 | ||
| T3 | 1.19 | 0.66, 2.12 | ||
| T4 | 2.04 | 1.24, 3.44 | ||
| Chemotherapy Treatment | 200 | 0.4 | ||
| Drug A | — | — | ||
| Drug B | 1.18 | 0.81, 1.71 | ||
| Tumor Response | 193 | 0.008 | ||
| no | — | — | ||
| yes | 0.56 | 0.35, 0.86 | ||
|
1
IRR = Incidence Rate Ratio, CI = Confidence Interval |
||||
46.2 Deuxième exemple (données agrégées)
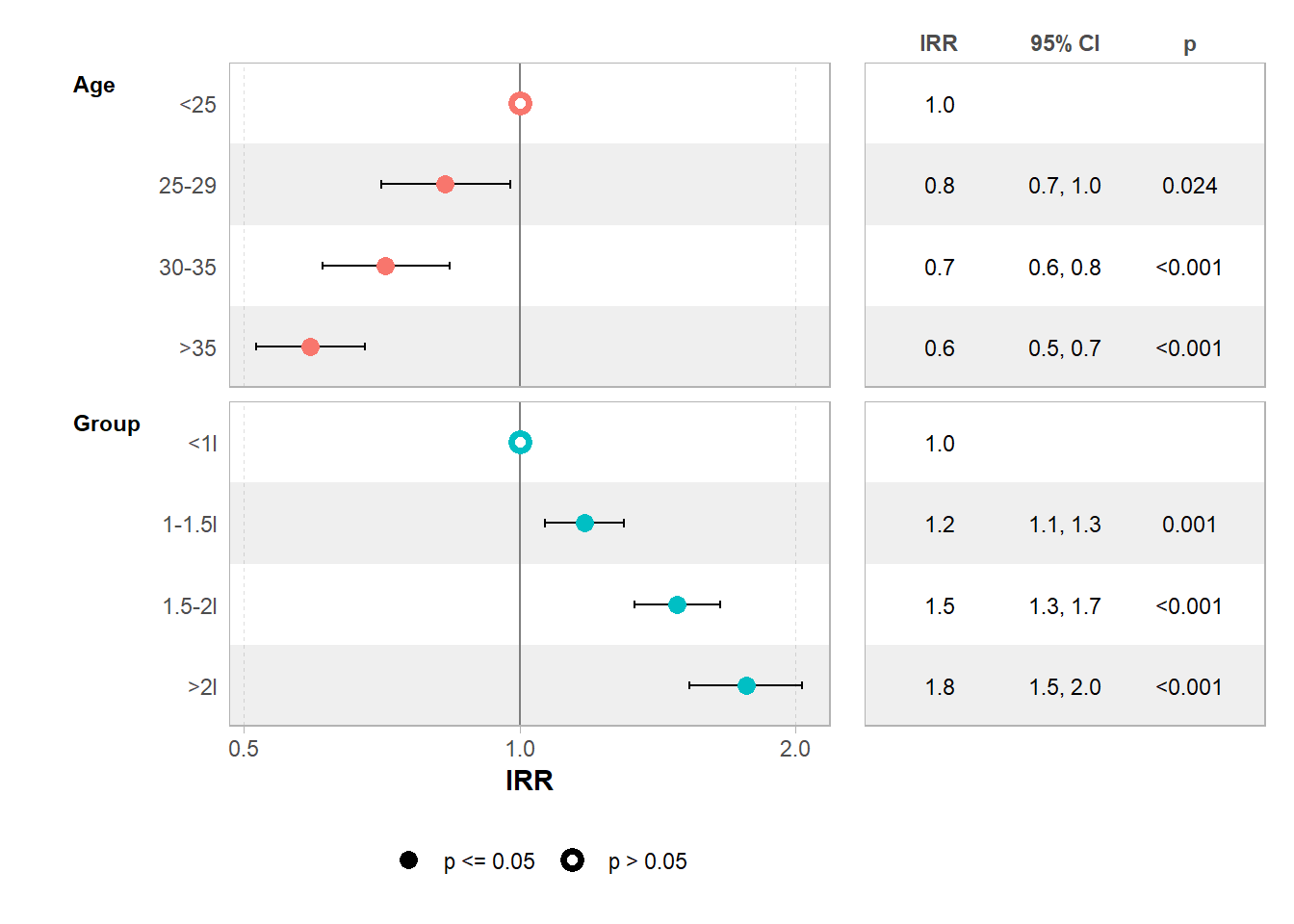
Pour ce second exemple, nous allons considérer le jeu de données MASS::Insurance qui provient d’une compagnie d’assurance américaine et porte sur le troisième trimestre 1973. Il indique le nombre de demande d’indemnisations (Claims) parmi les assurés pour leur voiture (Holders) en fonction de leur groupe d’âges (Age) et de la taille de la cylindrée de la voiture (Group). Nous cherchons à identifier les facteurs associés au taux de réclamation. Préparons rapidement les données et définissons notre modèle.
d <- MASS::Insurance
d$Age <- factor(d$Age, ordered = FALSE)
d$Group <- factor(d$Group, ordered = FALSE)
mod2_poisson <- glm(
Claims ~ Age + Group + offset(log(Holders)),
family = poisson,
data = d
)
mod2_poisson |>
performance::check_overdispersion()# Overdispersion test
dispersion ratio = 1.140
Pearson's Chi-Squared = 65.003
p-value = 0.218No overdispersion detected.Regardons les résultats.
Le taux de réclamation diminue avec l’âge de l’assuré (il est 40% moindre pour les assurés de plus de 35 ans par rapport à ceux de moins de 25 ans) et augmente avec la cylindrée de la voiture (il est 80% plus élevé pour les véhicules avec une cylindrée de plus de 2 litres par rapport aux véhicules avec une cylindrée de moins d’1 litre).
46.3 Troisième exemple (données individuelles, évènement unique)
Pour notre troisième exemple, nous allons reprendre les données de fécondité présentée au chapitre précédent (cf. Chapitre 45) et venant d’une enquête transversale rétrospective menée auprès de femmes âgées de 15 à 49 ans.
Nous allons nous intéresser au taux de fécondité entre 15 et 24 ans révolus (soit entre 15 et 25 ans exacts) et intégrer à l’analyse les femmes de moins de 25 ans en tenant compte de leur durée d’exposition (différence entre l’âge à l’enquête et 15 ans). Nous allons donc calculer la durée d’exposition comme exposition = if_else(age <= 25, age - 15, 10) puisque, pour les femmes de plus de 25 ans à l’enquête, la durée d’exposition entre 15 et 25 ans exacts est de 10 ans.
library(tidyverse)
library(labelled)
data("fecondite", package = "questionr")
femmes <-
femmes |>
unlabelled() |>
mutate(
age = time_length(
date_naissance %--% date_entretien,
unit = "years"
),
exposition = if_else(age <= 25, age - 15, 10),
educ2 = educ |>
fct_recode(
"secondaire/supérieur" = "secondaire",
"secondaire/supérieur" = "supérieur"
)
) |>
# exclure celles qui viennent juste d'avoir 15 ans
filter(exposition > 0)Comptons maintenant le nombre de naissances entre 15 et 25 ans exacts.
enfants <-
enfants |>
unlabelled() |>
left_join(
femmes |>
select(id_femme, date_naissance_mere = date_naissance),
by = "id_femme"
) |>
mutate(
age_mere = time_length(
date_naissance_mere %--% date_naissance,
unit = "years"
)
)
femmes <-
femmes |>
left_join(
enfants |>
filter(age_mere >= 15 & age_mere < 25) |>
group_by(id_femme) |>
count(name = "enfants_15_24"),
by = "id_femme"
) |>
tidyr::replace_na(list(enfants_15_24 = 0L))Calculons maintenant notre modèle.
Vérifions la surdispersion.
# Overdispersion test
dispersion ratio = 1.368
Pearson's Chi-Squared = 2723.252
p-value = < 0.001Overdispersion detected.Le test indique de la surdispersion. Optons donc pour un modèle négatif binomial.
mod3_nb <- MASS::glm.nb(
enfants_15_24 ~ educ2 + milieu + offset(log(exposition)),
data = femmes
)
mod3_nb |>
performance::check_overdispersion()# Overdispersion test
dispersion ratio = 0.822
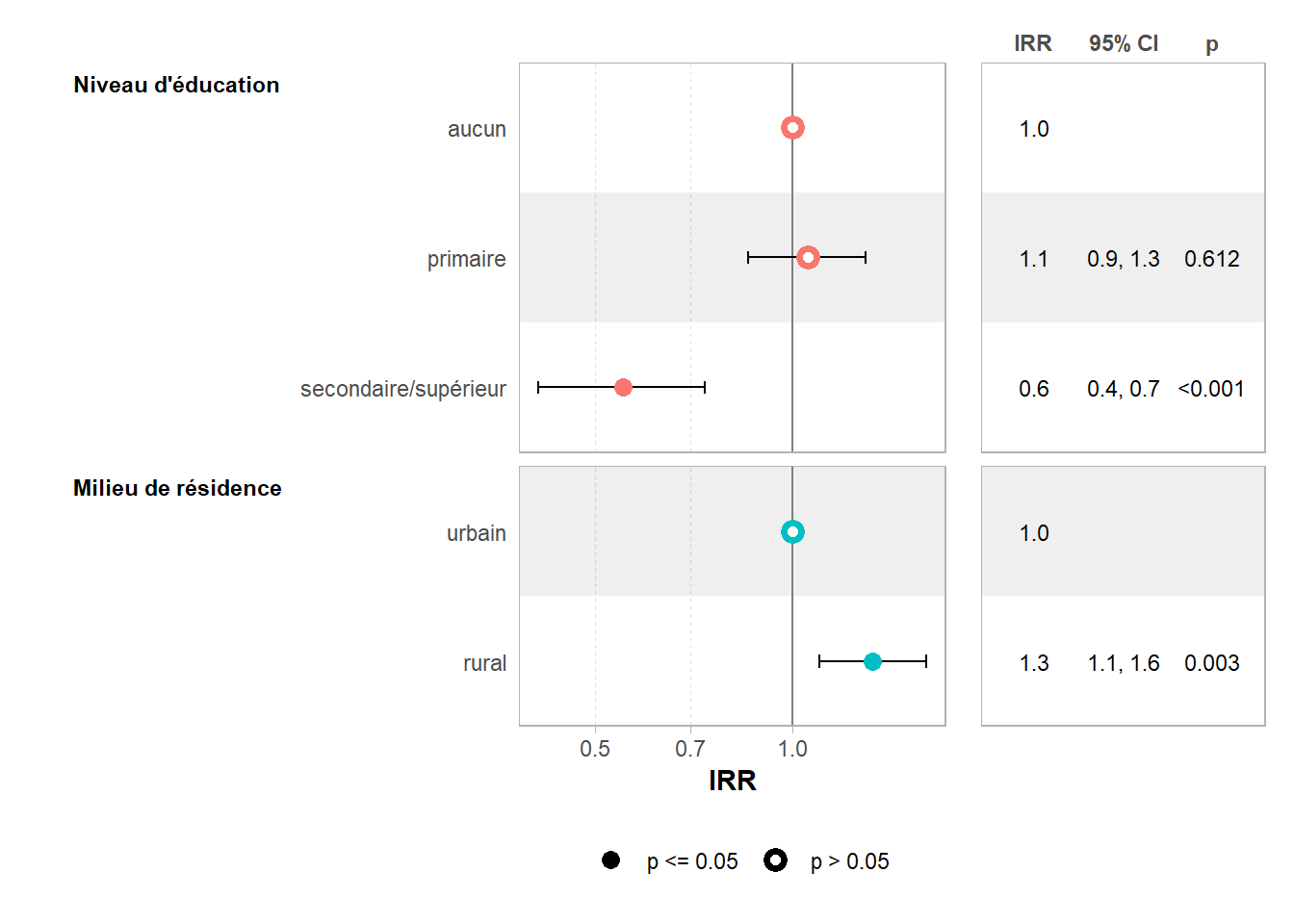
p-value = 0.016Underdispersion detected.Nous pouvons maintenant regarder les résultats.
46.4 Tuto@Mate
Les modèles d’incidence sont présentés sur YouTube dans le Tuto@Mate#62.
46.5 Lectures complémentaires
- Tutoriel : GLM sur données de comptage (régression de Poisson) avec R par Claire Della Vedova
- Zoom sur la Regression de Poisson et l’Incidence Risque Ratio (IRR) : exemple du vaccin anti-SarsCov2 d’Oxford par Ihsane Hmamouchi