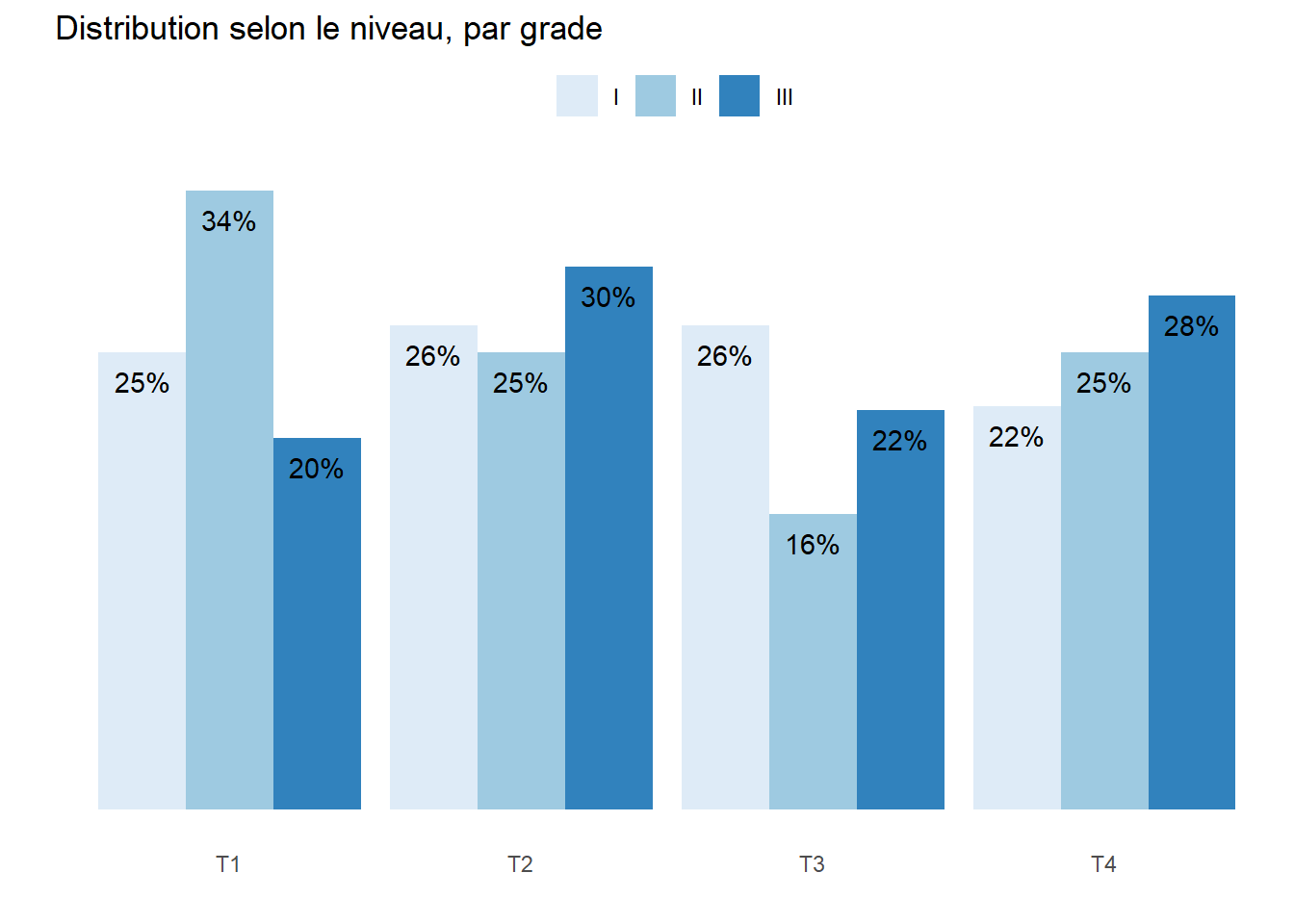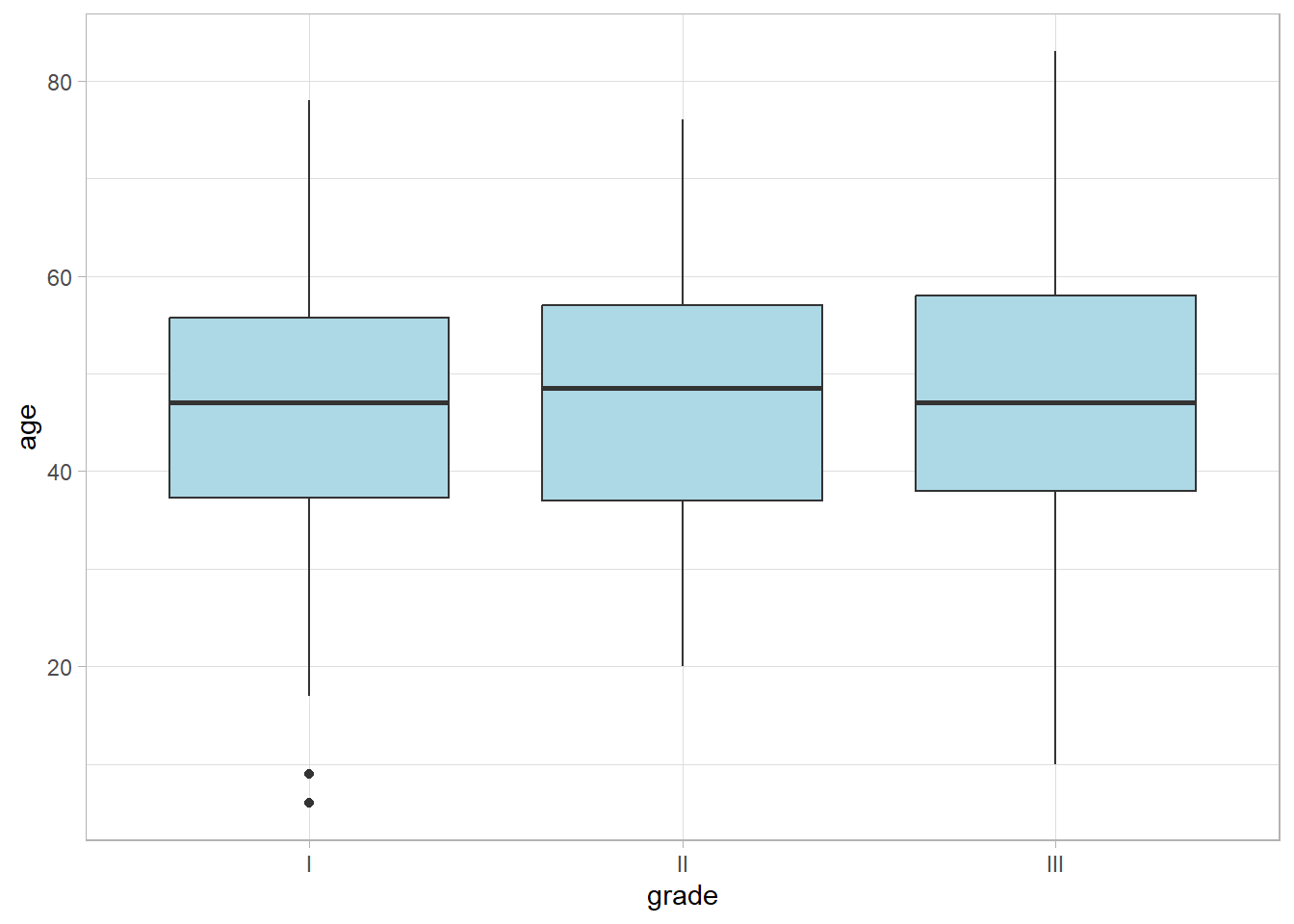Setting theme "language: fr"19 Statistique bivariée & Tests de comparaison
19.1 Deux variables catégorielles
19.1.1 Tableau croisé avec gtsummary
Pour regarder le lien entre deux variables catégorielles, l’approche la plus fréquente consiste à réaliser un tableau croisé, ce qui s’obtient très facilement avec l’argument by de la fonction gtsummary::tbl_summary() que nous avons déjà abordée dans le chapitre sur la statistique univariée (cf. Section 18.2).
Commençons par appeler gtsummary et à définir un thème par défaut.
Prenons pour exemple le jeu de données gtsummary::trial et croisons les variables stage et grade. On indique à by la variable à représenter en colonnes et à include celle à représenter en lignes.
| Caractéristique |
I N = 681 |
II N = 681 |
III N = 641 |
|---|---|---|---|
| T Stage | |||
| T1 | 25,0% (17) | 33,8% (23) | 20,3% (13) |
| T2 | 26,5% (18) | 25,0% (17) | 29,7% (19) |
| T3 | 26,5% (18) | 16,2% (11) | 21,9% (14) |
| T4 | 22,1% (15) | 25,0% (17) | 28,1% (18) |
| 1 | |||
Par défaut, les pourcentages affichés correspondent à des pourcentages en colonne. On peut demander des pourcentages en ligne avec percent = "row" ou des pourcentages du total avec percent = "cell".
Il est possible de passer plusieurs variables à include mais une seule variable peut être transmise à by. La fonction gtsummary::add_overall() permet d’ajouter une colonne totale. Comme pour un tri à plat, on peut personnaliser les statistiques affichées avec statistic.
library(gtsummary)
trial |>
tbl_summary(
include = c(stage, trt),
by = grade,
statistic = ~ "{p}% ({n}/{N})",
percent = "row"
) |>
add_overall(last = TRUE)| Caractéristique |
I N = 681 |
II N = 681 |
III N = 641 |
Total (N = 200)1 |
|---|---|---|---|---|
| T Stage | ||||
| T1 | 32,1% (17/53) | 43,4% (23/53) | 24,5% (13/53) | 100,0% (53/53) |
| T2 | 33,3% (18/54) | 31,5% (17/54) | 35,2% (19/54) | 100,0% (54/54) |
| T3 | 41,9% (18/43) | 25,6% (11/43) | 32,6% (14/43) | 100,0% (43/43) |
| T4 | 30,0% (15/50) | 34,0% (17/50) | 36,0% (18/50) | 100,0% (50/50) |
| Chemotherapy Treatment | ||||
| Drug A | 35,7% (35/98) | 32,7% (32/98) | 31,6% (31/98) | 100,0% (98/98) |
| Drug B | 32,4% (33/102) | 35,3% (36/102) | 32,4% (33/102) | 100,0% (102/102) |
| 1 | ||||
Choisissez bien votre type de pourcentages (en lignes ou en colonnes). Si d’un point de vue purement statistique, ils permettent tous deux de décrire la relation entre les deux variables, ils ne correspondent au même story telling. Tout dépend donc du message que vous souhaitez faire passer, de l’histoire que vous souhaitez raconter.
gtsummary::tbl_summary() est bien adaptée dans le cadre d’une analyse de facteurs afin de représenter un outcome indiqué avec by et une liste de facteurs avec include.
Lorsque l’on ne croise que deux variables et que l’on souhaite un affichage un peu plus traditionnel
d’un tableau croisé, on peut utiliser gtsummary::tbl_cross() à laquelle on transmettra une et une seule variable à row et une et une seule variable à col. Pour afficher des pourcentages, il faudra indiquer le type de pourcentages voulus avec percent.
Grade
|
Total | |||
|---|---|---|---|---|
| I | II | III | ||
| T Stage | ||||
| T1 | 17 (32,1%) | 23 (43,4%) | 13 (24,5%) | 53 (100,0%) |
| T2 | 18 (33,3%) | 17 (31,5%) | 19 (35,2%) | 54 (100,0%) |
| T3 | 18 (41,9%) | 11 (25,6%) | 14 (32,6%) | 43 (100,0%) |
| T4 | 15 (30,0%) | 17 (34,0%) | 18 (36,0%) | 50 (100,0%) |
| Total | 68 (34,0%) | 68 (34,0%) | 64 (32,0%) | 200 (100,0%) |
19.1.2 Représentations graphiques (cas général)
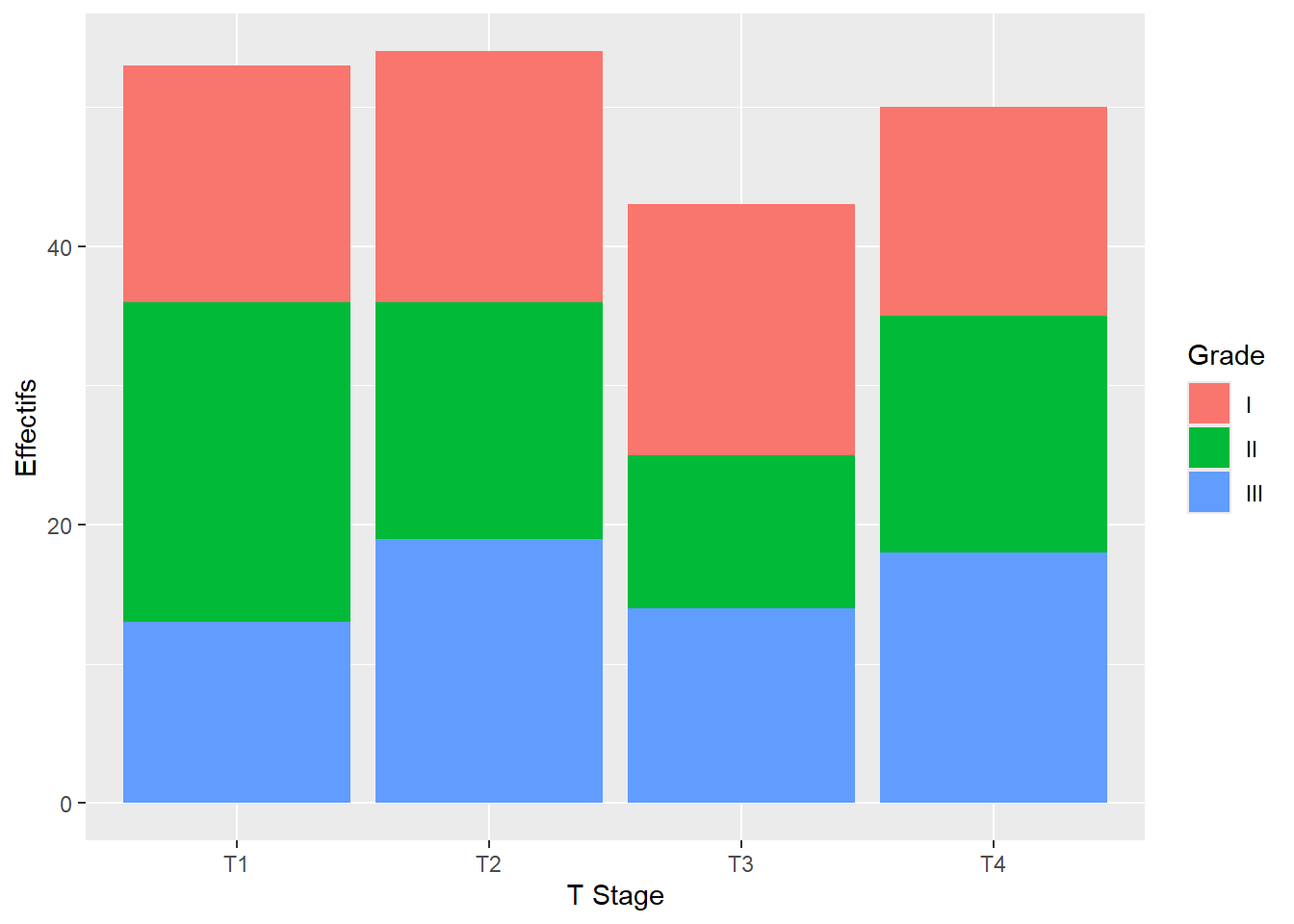
La représentation graphique la plus commune pour le croisement de deux variables catégorielles est le diagramme en barres, que l’on réalise avec la géométrie ggplot2::geom_bar() et en utilisant les esthétiques x et fill pour représenter les deux variables.
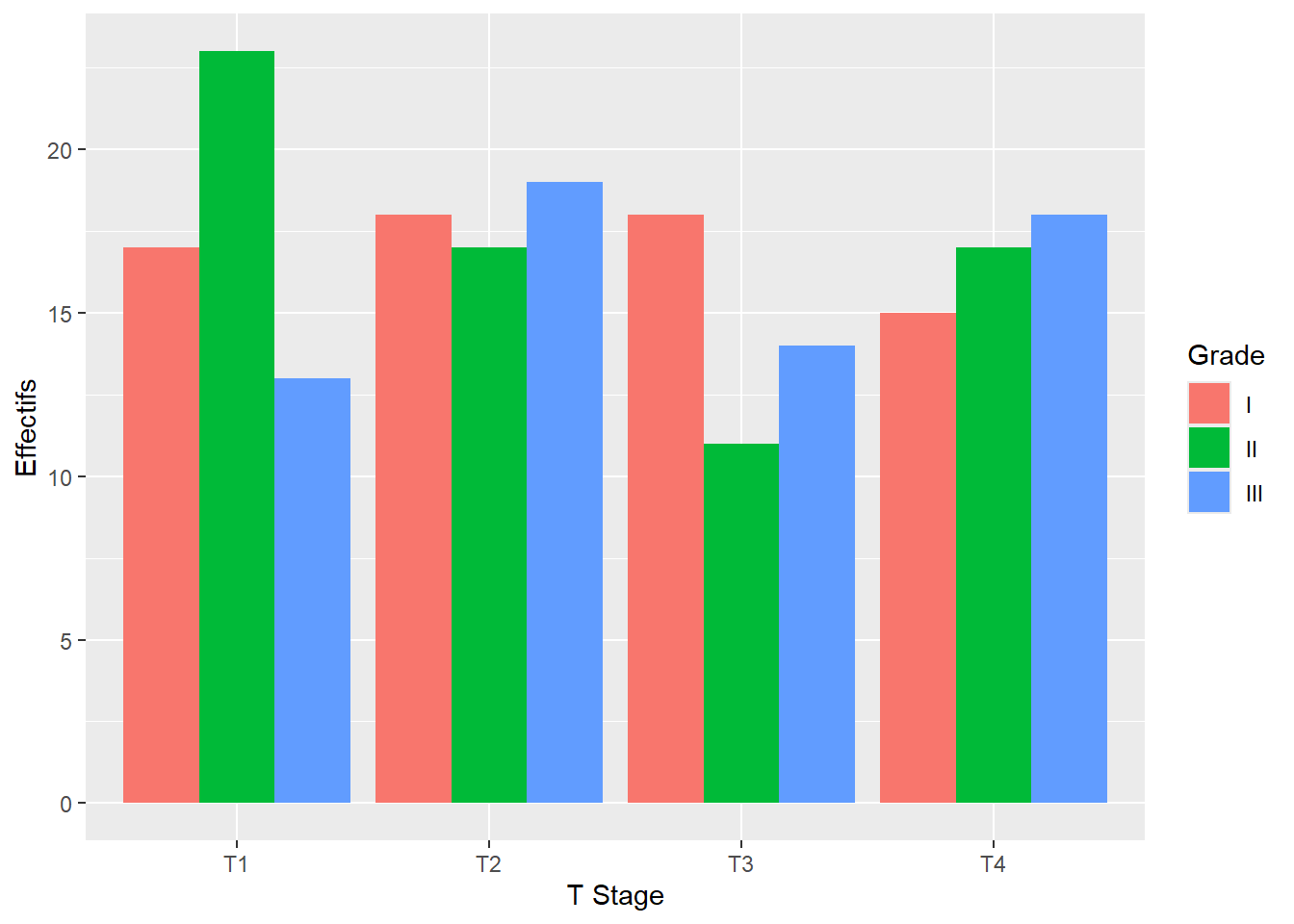
On peut modifier la position des barres avec le paramètre position.
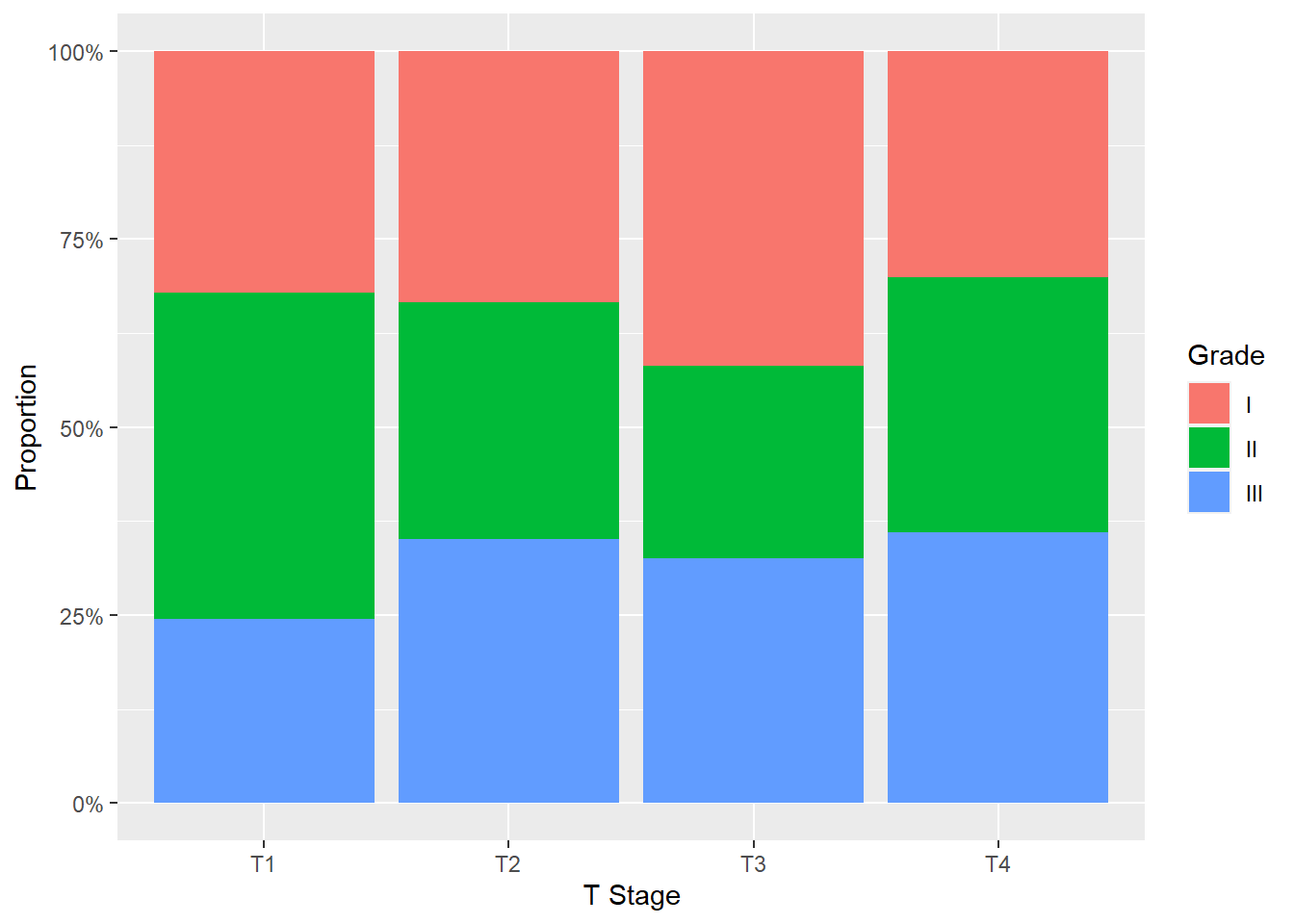
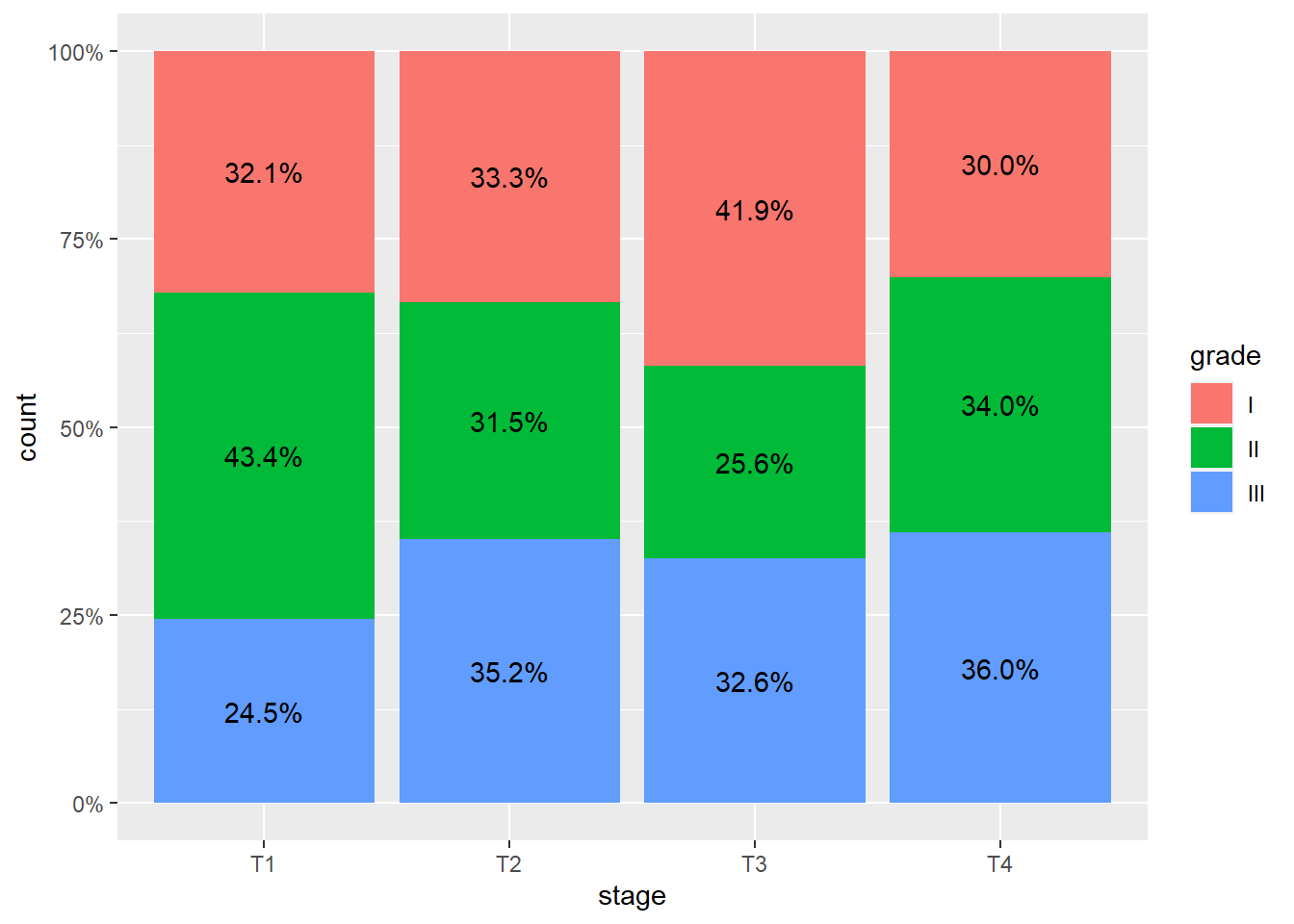
Pour des barres cumulées, on aura recours à position = "fill". Pour que les étiquettes de l’axe des y soient représentées sous forme de pourcentages (i.e. 25% au lieu de 0.25), on aura recours à la fonction scales::percent() qui sera transmise à ggplot2::scale_y_continuous().
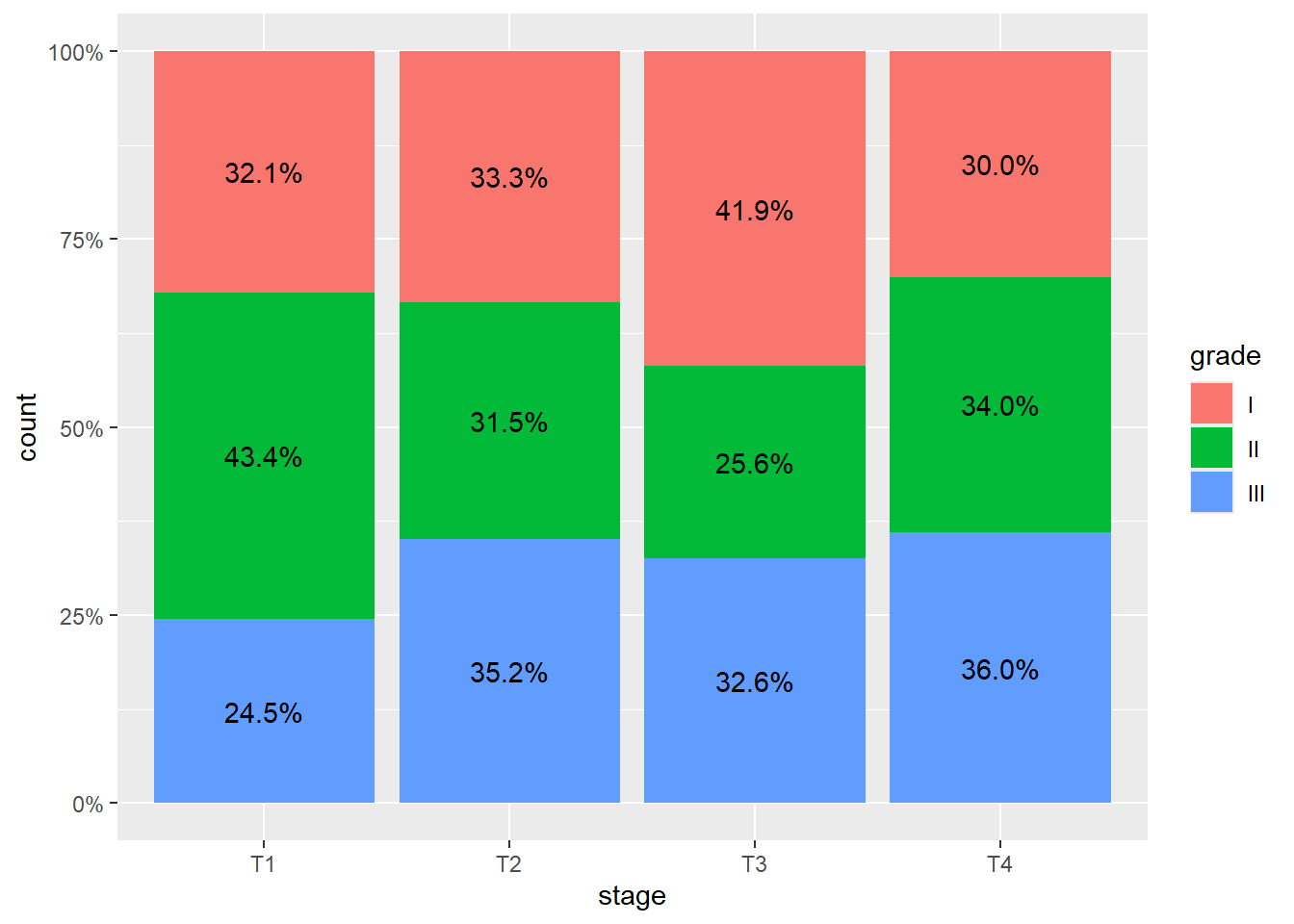
Il est facile d’ajouter des étiquettes en ayant recours à ggplot2::geom_text(), à condition de lui passer les bons paramètres.
Tout d’abord, il faudra préciser stat = "count" pour indiquer que l’on souhaite utiliser la statistique ggplot2::stat_count() qui est celle utilisé par défaut par ggplot2::geom_bar(). C’est elle qui permets de compter le nombre d’observations.
Il faut ensuite utiliser l’esthétique label pour indiquer ce que l’on souhaite afficher comme étiquettes. La fonction after_stat(count) permet d’accéder à la variable count calculée par ggplot2::stat_count().
Enfin, il faut indiquer la position verticale avec ggplot2::position_stack(). En précisant un ajustement de vertical de 0.5, on indique que l’on souhaite positionner l’étiquette au milieu.
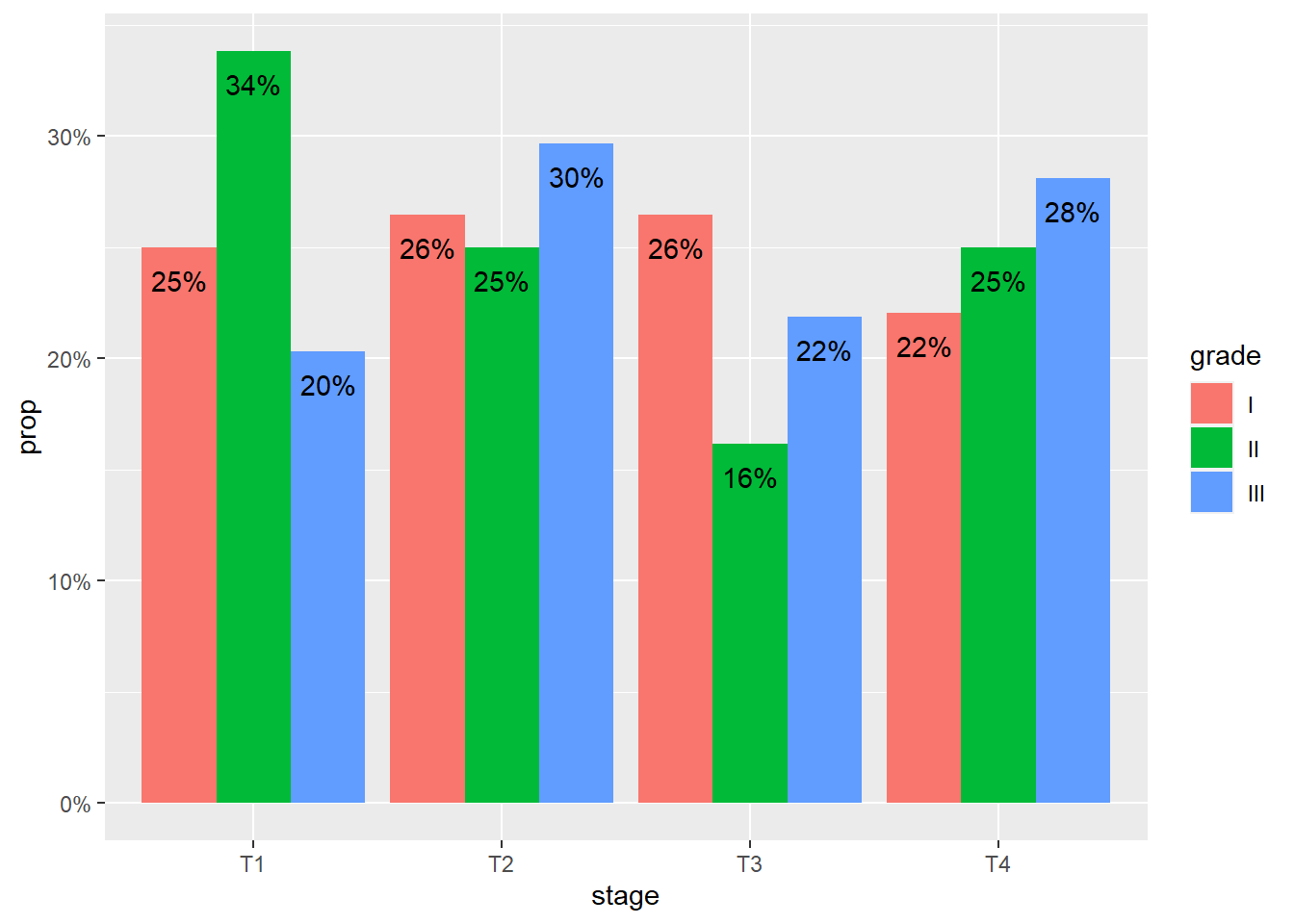
Pour un graphique en barres cumulées, on peut utiliser de manière similaire ggplot2::position_fill(). On ne peut afficher directement les proportions avec ggplot2::stat_count(). Cependant, nous pouvons avoir recours à ggstats::stat_prop(), déjà évoquée dans le chapitre sur la statistique univariée (cf. Section 18.1.2) et dont le dénominateur doit être précisé via l’esthétique by.
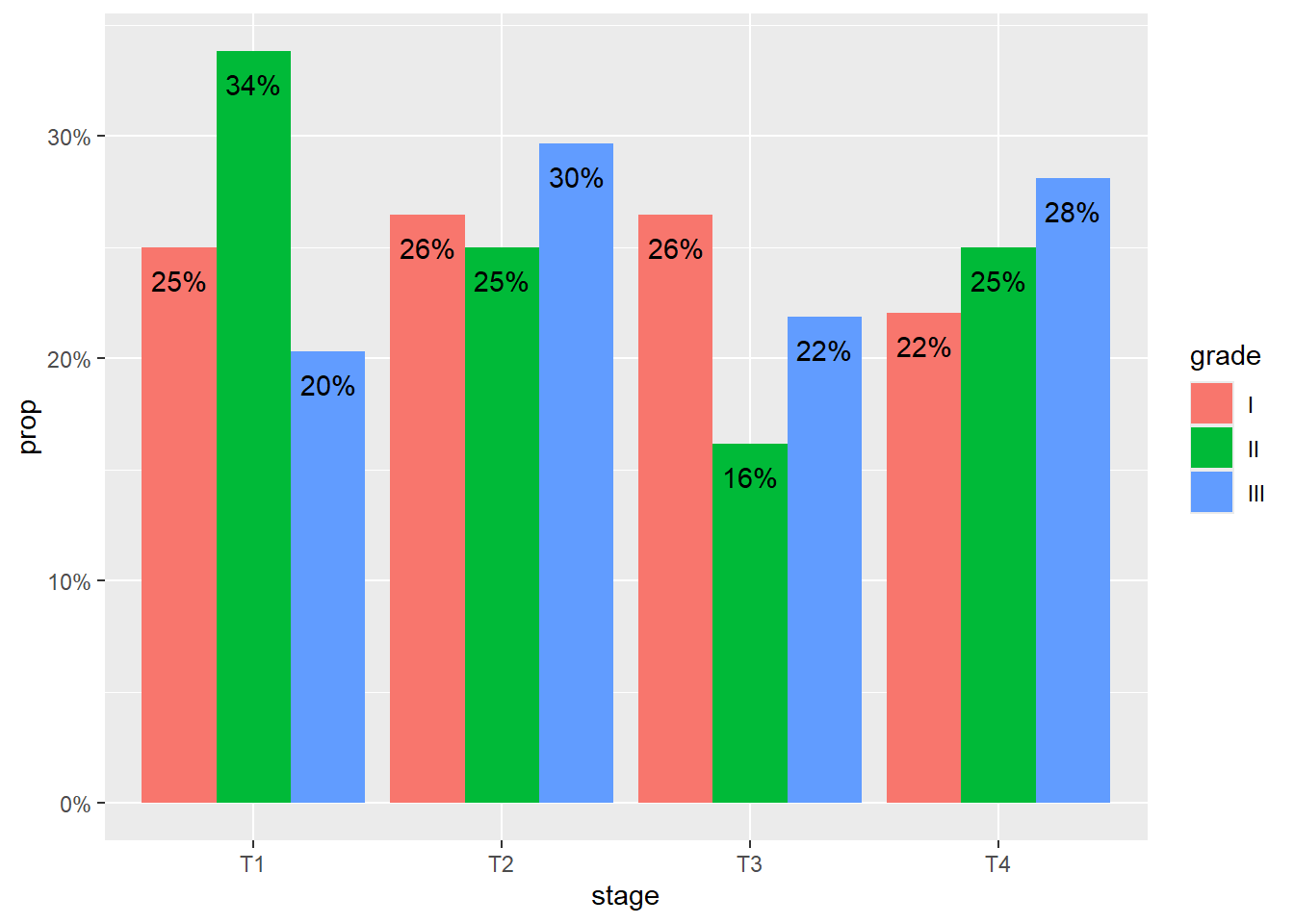
On peut aussi comparer facilement deux distributions, ici la proportion de chaque stade de cancer au sein chaque grade.
p <- ggplot(trial) +
aes(
x = stage,
y = after_stat(prop),
fill = grade,
by = grade,
label = scales::percent(after_stat(prop), accuracy = 1)
) +
geom_bar(
stat = "prop",
position = position_dodge(.9)
) +
geom_text(
aes(y = after_stat(prop) - 0.01),
stat = "prop",
position = position_dodge(.9),
vjust = "top"
) +
scale_y_continuous(labels = scales::percent)
pIl est possible d’alléger le graphique en retirant des éléments superflus.
Le diaporama ci-dessous vous permet de visualiser chaque étape du code correspondant au graphique précédent.
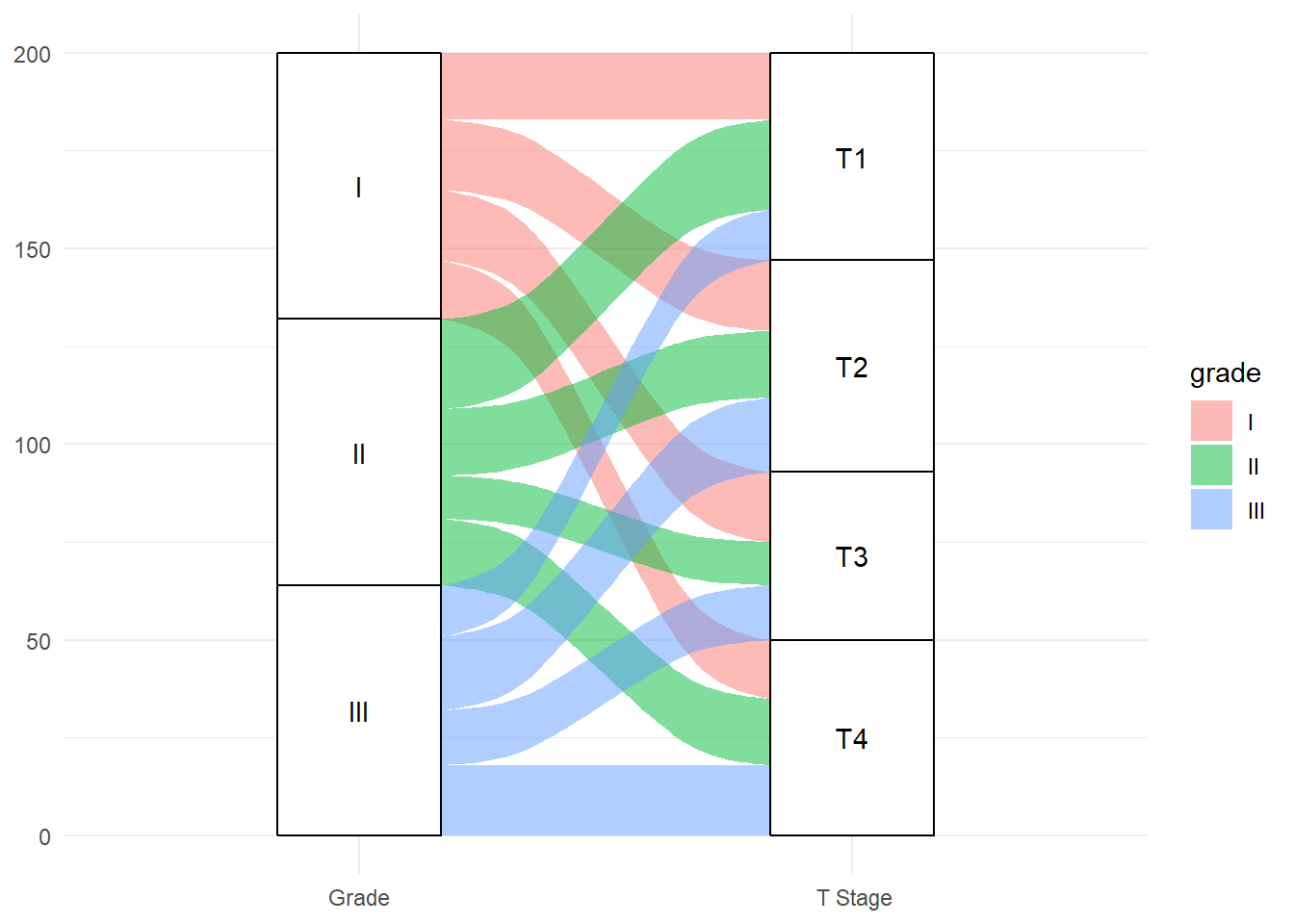
Une représentation alternative du croisement de deux variables est à d’avoir recours à un diagramme alluvial1. Ce type de graphique est particulièrement adapté pour des données temporelles, par exemple du type avant / après
. Il peut également être étendu à un plus grand nombre d’étapes. Ci-dessous, un exemple reposants sur le package ggalluvial.
1 Un graphique alluvial est une variation d’un graphique de Sankey. Usuellement, un graphique de Sankey espace verticalement les différents statuts d’une même étape, tandis qu’il n’y a pas d’espace vertical dans un diagramme alluvial. Le package {ggsankey} propose une implémentation à la fois des diagrammes de Sankey des diagrammes alluviaux. Ce package n’est cependant pas disponible sur CRAN et doit être installé manuellement depuis GitHub. Pour un diagramme de Sankey, on pourra également avoir recours à ggforce::geom_parallel_sets() du package ggforce. Cette fonction nécessite une réorganisation des données dans un format long au préalable.
19.1.3 Représentations graphiques avec guideR
Le package guideR, le compagnon de guide-R, fournit plusieurs fonctions graphiques pour rapidement comparer une variable selon un ou plusieurs sous-groupe.
Pour une variable catégorielle, on aura recours à la fonction guideR::plot_categorical(). Sa syntaxe suit les usages du tidyverse. On lui passe un jeu de données, puis on indique l’outcome et enfin une liste de variables de croisement avec by.
Il s’agit d’un graphique en barres cumulées. La distribution générale est calculée globalement pour l’ensemble de l’échantillon puis pour chacune des modalités des variables transmises à by. Comme on peut le voir ici, si l’on passe une variable continue à by (ici la variable marker), celle-ci est transformée en variable catégorielle à la volée en utilisant les quartiles. La fonction affiche aussi par défaut la p-valeur d’un test de comparaison (ici un test exact de Fisher). Les tests de comparaison seront vu un peu plus loin dans ce chapitre. Notons également que la fonction prend en compte les étiquettes de variables pour améliorer l’affichage.
Les barres verticales ne sont pas toujours très lisibles avec des noms de modalité longs. On pourra inverser l’axe des X et celui des Y avec flip = TRUE. L’option minimal = TRUE permet d’alléger visuellement le graphique. On peut personnaliser l’étiquette de la catégorie Overall avec overall_label. L’option drop_na_by permet d’exclure les valeurs manquantes pour les variables définies via by. Enfin, l’option pvalues_test permet de modifier le type de test statistique (dans l’exemple suivant on utilise le test du Chi²).
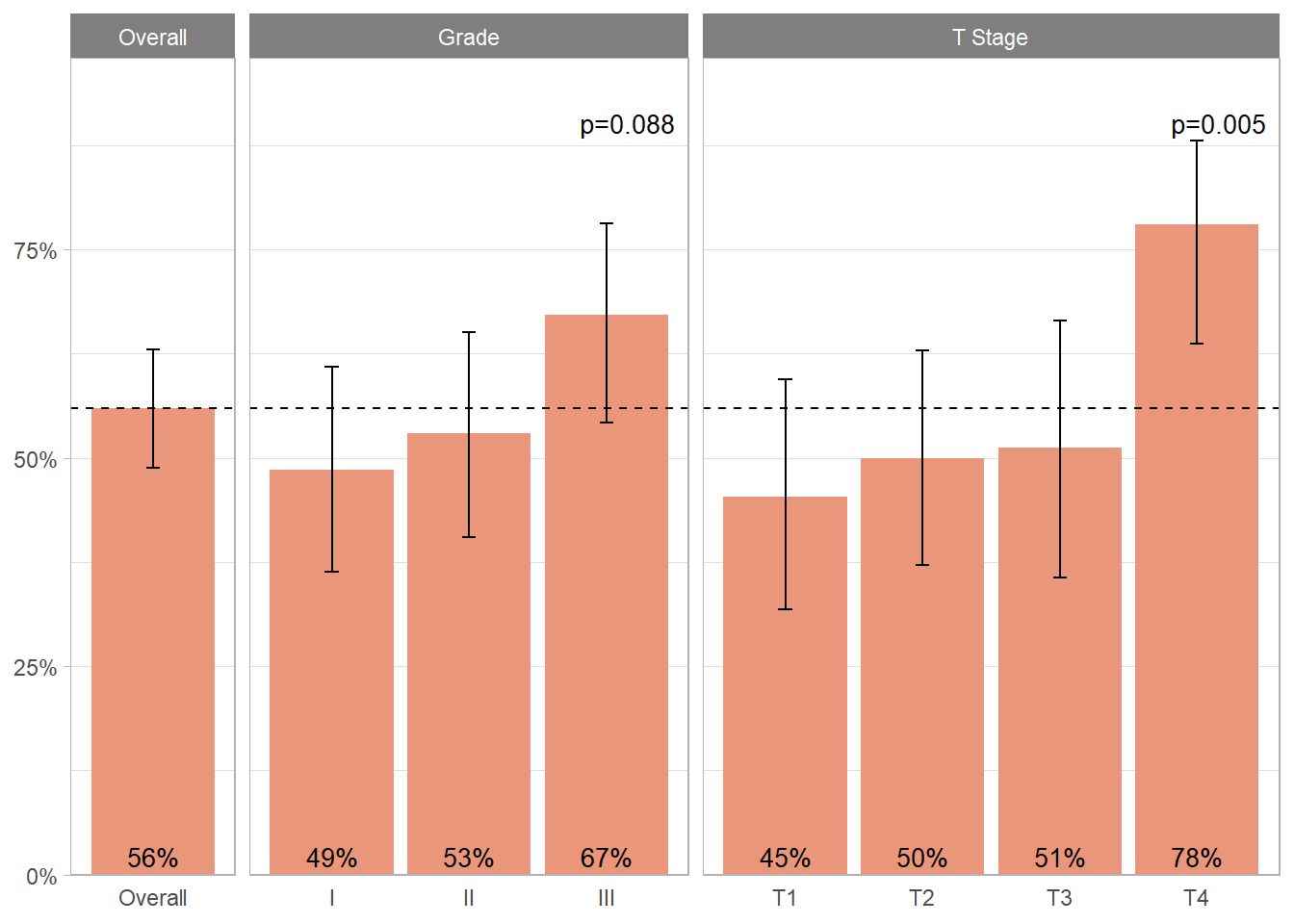
Pour croiser une proportion simple (variable binaire), on pourra avoir recours à la fonction guideR::plot_proportions(). Pour cela, on indiquera une condition définissant la proportion à représenter et, éventuellement, une liste de variables de croisement. Cette fonction a l’avantage de représenter également les intervalles de confiance à 95% ainsi que des tests de comparaison (voir ci-après). Pour plus d’information sur les différentes options disponibles, voir l’aide de la fonction.
19.1.4 Calcul manuel
Les deux fonctions de base permettant le calcul d’un tri à plat sont table() et xtabs() (cf. Section 18.3.2). Ces mêmes fonctions permettent le calcul du tri croisé de deux variables (ou plus). Pour table(), on passera les deux vecteurs à croisés, tandis que pour xtabs() on décrira le tableau attendu à l’aide d’une formule.
I II III
T1 17 23 13
T2 18 17 19
T3 18 11 14
T4 15 17 18 grade
stage I II III
T1 17 23 13
T2 18 17 19
T3 18 11 14
T4 15 17 18Le tableau obtenu est basique et ne contient que les effectifs. La fonction addmargins() permet d’ajouter les totaux par ligne et par colonne.
grade
stage I II III Sum
T1 17 23 13 53
T2 18 17 19 54
T3 18 11 14 43
T4 15 17 18 50
Sum 68 68 64 200Pour le calcul des pourcentages, le plus simple est d’avoir recours au package questionr qui fournit les fonctions questionr::cprop(), questionr::rprop() et questionr::prop() qui permettent de calculer, respectivement, les pourcentages en colonne, en ligne et totaux.
grade
stage I II III Ensemble
T1 25.0 33.8 20.3 26.5
T2 26.5 25.0 29.7 27.0
T3 26.5 16.2 21.9 21.5
T4 22.1 25.0 28.1 25.0
Total 100.0 100.0 100.0 100.0 grade
stage I II III Total
T1 32.1 43.4 24.5 100.0
T2 33.3 31.5 35.2 100.0
T3 41.9 25.6 32.6 100.0
T4 30.0 34.0 36.0 100.0
Ensemble 34.0 34.0 32.0 100.0 grade
stage I II III Total
T1 8.5 11.5 6.5 26.5
T2 9.0 8.5 9.5 27.0
T3 9.0 5.5 7.0 21.5
T4 7.5 8.5 9.0 25.0
Total 34.0 34.0 32.0 100.0Si l’on a besoin des différents résultats dans un tableau de données, le plus simple avec d’avoir recours à la fonction guideR::proportion() fournie dans guideR le package compagnon de guide-R.
Si on lui passe une simple liste des variables, on obtient des pourcentages du total.
# A tibble: 12 × 5
stage grade n N prop
<fct> <fct> <int> <int> <dbl>
1 T1 I 17 200 8.5
2 T1 II 23 200 11.5
3 T1 III 13 200 6.5
4 T2 I 18 200 9
5 T2 II 17 200 8.5
6 T2 III 19 200 9.5
7 T3 I 18 200 9
8 T3 II 11 200 5.5
9 T3 III 14 200 7
10 T4 I 15 200 7.5
11 T4 II 17 200 8.5
12 T4 III 18 200 9 Mais l’on peut contrôler la manière de calculer les pourcentages avec le paramètre .by. Ainsi, pour la répartition par stade selon le grade :
# A tibble: 12 × 5
# Groups: grade [3]
grade stage n N prop
<fct> <fct> <int> <int> <dbl>
1 I T1 17 68 25
2 I T2 18 68 26.5
3 I T3 18 68 26.5
4 I T4 15 68 22.1
5 II T1 23 68 33.8
6 II T2 17 68 25
7 II T3 11 68 16.2
8 II T4 17 68 25
9 III T1 13 64 20.3
10 III T2 19 64 29.7
11 III T3 14 64 21.9
12 III T4 18 64 28.1La fonction guideR::proportion() peut également être utilisée pour des tableaux à 3 entrées ou plus.
19.1.5 Test du Chi² et dérivés
Dans le cadre d’un tableau croisé, on peut tester l’existence d’un lien entre les modalités de deux variables, avec le très classique test du Chi² (parfois écrit χ² ou Chi²). Pour une présentation plus détaillée du test, on pourra se référer à ce cours de Julien Barnier.
Le test du Chi² peut se calculer très facilement avec la fonction chisq.test() appliquée au tableau obtenu avec table() ou xtabs().
grade
stage I II III
T1 17 23 13
T2 18 17 19
T3 18 11 14
T4 15 17 18
Pearson's Chi-squared test
data: tab
X-squared = 4.8049, df = 6, p-value = 0.5691Si l’on est adepte de gtsummary, il suffit d’appliquer gtsummary::add_p() au tableau produit avec gtsummary::tbl_summary().
| Caractéristique |
I N = 681 |
II N = 681 |
III N = 641 |
p-valeur2 |
|---|---|---|---|---|
| T Stage | 0,6 | |||
| T1 | 25,0% (17) | 33,8% (23) | 20,3% (13) | |
| T2 | 26,5% (18) | 25,0% (17) | 29,7% (19) | |
| T3 | 26,5% (18) | 16,2% (11) | 21,9% (14) | |
| T4 | 22,1% (15) | 25,0% (17) | 28,1% (18) | |
| 1 | ||||
| 2 test du khi-deux d’indépendance | ||||
Dans notre exemple, les deux variables stage et grade ne sont clairement pas corrélées.
Un test alternatif est le test exact de Fisher. Il s’obtient aisément avec fisher.test() ou bien en le spécifiant via l’argument test de gtsummary::add_p().
Fisher's Exact Test for Count Data
data: tab
p-value = 0.5801
alternative hypothesis: two.sidedtrial |>
tbl_summary(
include = stage,
by = grade
) |>
add_p(test = all_categorical() ~ "fisher.test")| Caractéristique |
I N = 681 |
II N = 681 |
III N = 641 |
p-valeur2 |
|---|---|---|---|---|
| T Stage | 0,6 | |||
| T1 | 25,0% (17) | 33,8% (23) | 20,3% (13) | |
| T2 | 26,5% (18) | 25,0% (17) | 29,7% (19) | |
| T3 | 26,5% (18) | 16,2% (11) | 21,9% (14) | |
| T4 | 22,1% (15) | 25,0% (17) | 28,1% (18) | |
| 1 | ||||
| 2 test exact de Fisher | ||||
Formellement, le test de Fisher suppose que les marges du tableau (totaux lignes et colonnes) sont fixées, puisqu’il repose sur une loi hypergéométrique, et donc celui-ci se prête plus au cas des situations expérimentales (plans d’expérience, essais cliniques) qu’au cas des données tirées d’études observationnelles.
Historiquement, le test de Fisher a été conçu uniquement pour des tableaux 2 × 2 (deux lignes et deux colonnes). Il a par la suite été étendu au cas général. Ceci étant dit, pour certains tableaux assez grand, le calcul exact peut être compliqué. Auquel cas, il est préférable d’utiliser une simulation de Monte Carlo pour le calcul des p-valeurs. Cela se fait en indiquant simulate.p.value = TRUE quand on appelle la fonction fisher.test().
Quand on travaille avec gtsummary, le plus facile est d’utiliser le thème guideR::theme_gtsummary_fisher_simulate_p() fourni par guideR et qui applique alors automatiquement le test de Fisher avec simulation de Monte Carlo pour toutes les variables catégorielles lorsque l’on fait appel à add_p().
19.1.6 Comparaison de deux proportions
Pour comparer deux proportions, la fonction de base est prop.test() à laquelle on passera un tableau à 2×2 dimensions.
trt
I(stage == "T1") Drug A Drug B Ensemble
FALSE 71.4 75.5 73.5
TRUE 28.6 24.5 26.5
Total 100.0 100.0 100.0
2-sample test for equality of proportions with continuity correction
data: tab
X-squared = 0.24047, df = 1, p-value = 0.6239
alternative hypothesis: two.sided
95 percent confidence interval:
-0.2217278 0.1175050
sample estimates:
prop 1 prop 2
0.4761905 0.5283019 Il est également envisageable d’avoir recours à un test exact de Fisher. Dans le cas d’un tableau à 2×2 dimensions, le test exact de Fisher ne teste pas si les deux proportions sont différents, mais plutôt si leur odds ratio (qui est d’ailleurs renvoyé par la fonction) est différent de 1.
Fisher's Exact Test for Count Data
data: tab
p-value = 0.5263
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.4115109 1.5973635
sample estimates:
odds ratio
0.8125409 Mais le plus simple reste encore d’avoir recours à gtsummary et à sa fonction gtsummary::add_difference() que l’on peut appliquer à un tableau où le paramètre by n’a que deux modalités. Pour la différence de proportions, il faut que les variables transmises à include soit dichotomiques.
| Caractéristique |
Drug A N = 981 |
Drug B N = 1021 |
Différence2 | 95% IC2 | p-valeur2 |
|---|---|---|---|---|---|
| Tumor Response | 29,5% (28) | 33,7% (33) | -4,2% | -18% – 9,9% | 0,6 |
| Manquant | 3 | 4 | |||
| 1 | |||||
| 2 2-sample test for equality of proportions with continuity correction | |||||
| Abréviation: IC = intervalle de confiance | |||||
Attention : si l’on passe une variable catégorielle à trois modalités ou plus, c’est la différence des moyennes standardisées (globale pour la variable) qui sera calculée et non la différence des proportions dans chaque groupe. À noter : l’extension smd car gtsummary utilise en interne la fonction smd::smd() pour ce calcul
| Caractéristique |
Drug A N = 981 |
Drug B N = 1021 |
Différence2 | 95% IC2 |
|---|---|---|---|---|
| Grade | 0,07 | -0,20 – 0,35 | ||
| I | 35,7% (35) | 32,4% (33) | ||
| II | 32,7% (32) | 35,3% (36) | ||
| III | 31,6% (31) | 32,4% (33) | ||
| 1 | ||||
| 2 Standardized Mean Difference | ||||
| Abréviation: IC = intervalle de confiance | ||||
Pour calculer la différence des proportions pour chaque modalité de grade, il est nécessaire de transformer, en amont, la variable catégorielle grade en trois variables dichotomiques (de type oui/non, une par modalité), ce qui peut se faire facilement avec la fonction fastDummies::dummy_cols() de l’extension fastDummies.
trial |>
fastDummies::dummy_cols("grade") |>
tbl_summary(
by = trt,
include = starts_with("grade_"),
digits = ~ c(0, 1)
) |>
add_difference()| Caractéristique |
Drug A N = 981 |
Drug B N = 1021 |
Différence2 | 95% IC2 | p-valeur2 |
|---|---|---|---|---|---|
| grade_I | 36% (35,0) | 32% (33,0) | 3,4% | -11% – 17% | 0,7 |
| grade_II | 33% (32,0) | 35% (36,0) | -2,6% | -17% – 11% | 0,8 |
| grade_III | 32% (31,0) | 32% (33,0) | -0,72% | -14% – 13% | >0,9 |
| 1 | |||||
| 2 2-sample test for equality of proportions with continuity correction | |||||
| Abréviation: IC = intervalle de confiance | |||||
19.2 Une variable continue selon une variable catégorielle
19.2.1 Tableau comparatif avec gtsummary
Dans le chapitre sur la statistique univariée (cf. Section 18.2), nous avons abordé comment afficher les statistiques descriptives d’une variable continue avec gtsummary::tbl_summary(). Pour comparer une variable continue selon plusieurs groupes définis par une variable catégorielle, il suffit d’utiliser le paramètre by :
| Caractéristique |
I N = 681 |
II N = 681 |
III N = 641 |
|---|---|---|---|
| Age | 47,0 (37,0, 56,0) | 48,5 (37,0, 57,0) | 47,0 (38,0, 58,0) |
| Manquant | 2 | 6 | 3 |
| 1 Médiane (Q1, Q3) | |||
La fonction gtsummary::add_overall() permet d’ajouter une colonne total
et gtsummary::modify_spanning_header() peut-être utilisé pour ajouter un en-tête de colonne.
trial |>
tbl_summary(
include = age,
by = grade
) |>
add_overall(last = TRUE) |>
modify_spanning_header(
all_stat_cols(stat_0 = FALSE) ~ "**Grade**"
)| Caractéristique |
Grade
|
Total (N = 200)1 | ||
|---|---|---|---|---|
|
I N = 681 |
II N = 681 |
III N = 641 |
||
| Age | 47,0 (37,0, 56,0) | 48,5 (37,0, 57,0) | 47,0 (38,0, 58,0) | 47,0 (38,0, 57,0) |
| Manquant | 2 | 6 | 3 | 11 |
| 1 Médiane (Q1, Q3) | ||||
Comme pour un tri à plat, on peut personnaliser les statistiques à afficher avec statistic.
trial |>
tbl_summary(
include = age,
by = grade,
statistic = all_continuous() ~ "{mean} ({sd})",
digits = all_continuous() ~ c(1, 1)
) |>
add_overall(last = TRUE)| Caractéristique |
I N = 681 |
II N = 681 |
III N = 641 |
Total (N = 200)1 |
|---|---|---|---|---|
| Age | 46,2 (15,2) | 47,5 (13,7) | 48,1 (14,1) | 47,2 (14,3) |
| Manquant | 2 | 6 | 3 | 11 |
| 1 Moyenne (ET) | ||||
19.2.2 Représentations graphiques (cas général)
La moyenne ou la médiane sont des indicateurs centraux et ne suffisent pas à rendre compte des différences de distribution d’une variable continue entre plusieurs sous-groupes.
Une représentation usuelle pour comparer deux distributions consiste à avoir recours à des boîtes à moustaches que l’on obtient avec ggplot2::geom_boxplot().
Le trait central représente la médiane, le rectangle est délimité par le premier et le troisième quartiles (i.e. le 25e et le 75e percentiles). Les traits verticaux vont jusqu’aux extrêmes (minimum et maximum) ou jusqu’à 1,5 fois l’intervalle interquartile. Si des points sont situés à plus d’1,5 fois l’intervalle interquartile au-dessus du 3e quartile ou en-dessous du 1er quartile, ils sont considérés comme des valeurs atypiques et représentés par un point. Dans l’exemple précédent, c’est le cas des deux plus petites valeurs observées pour le grade I.
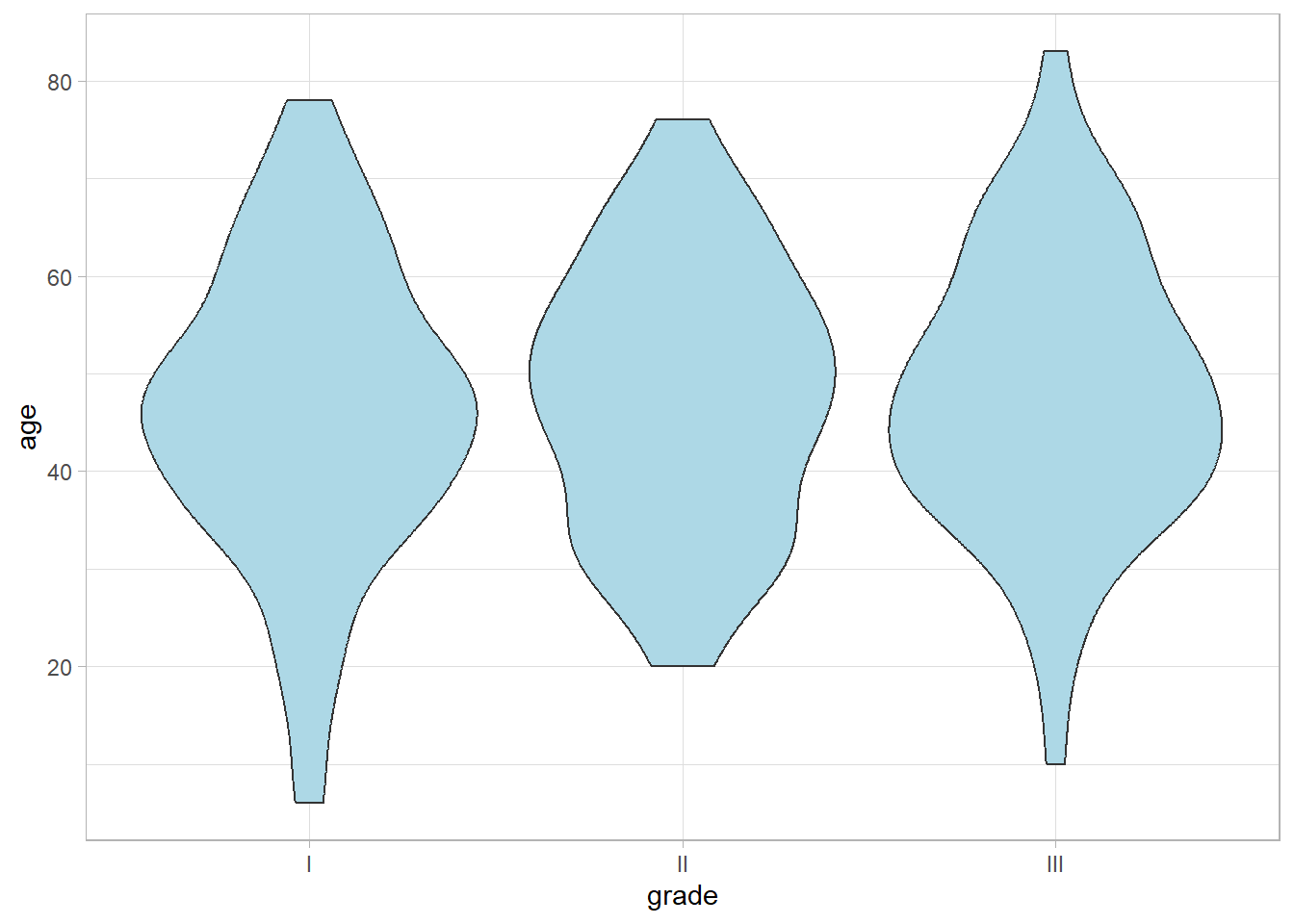
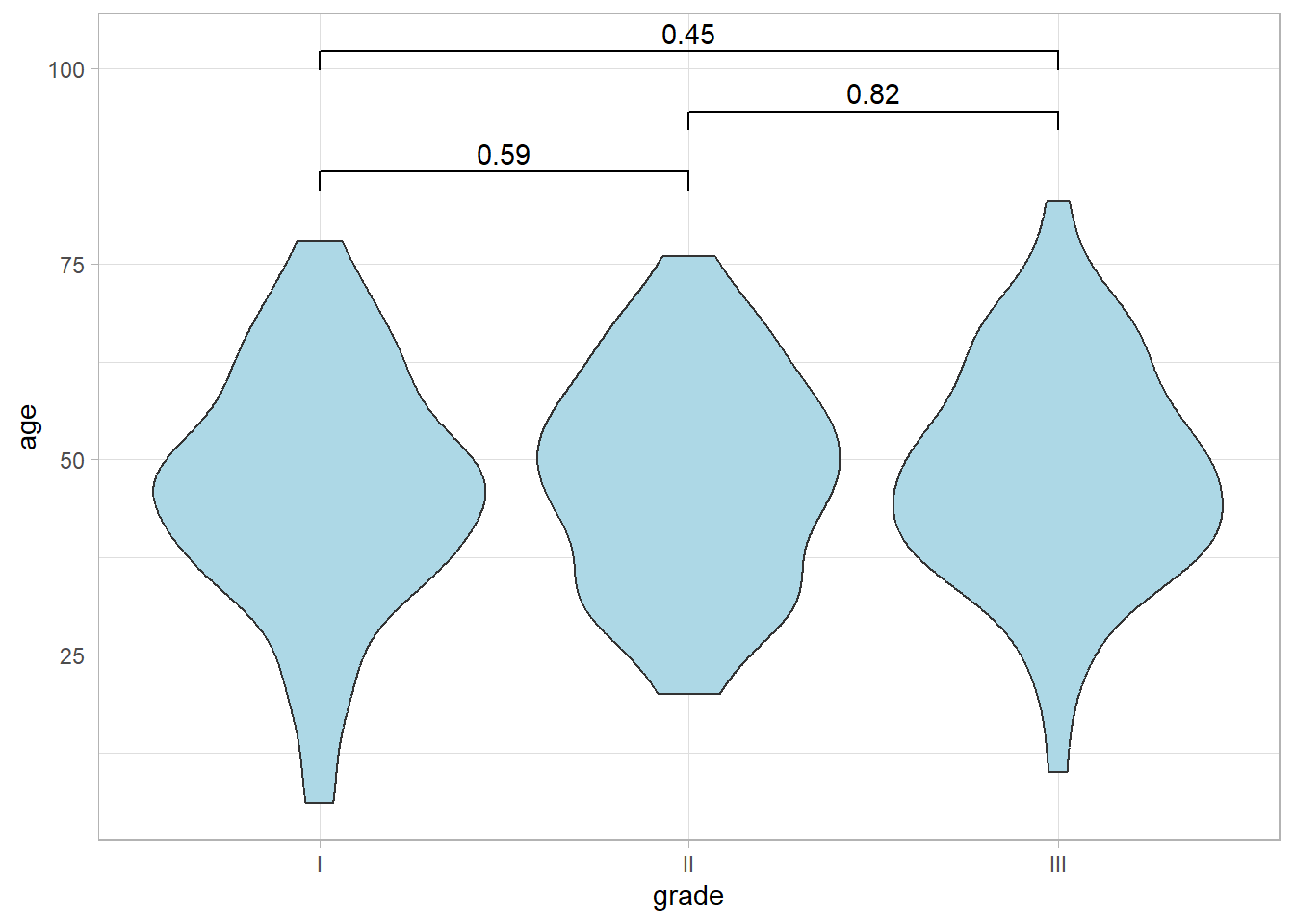
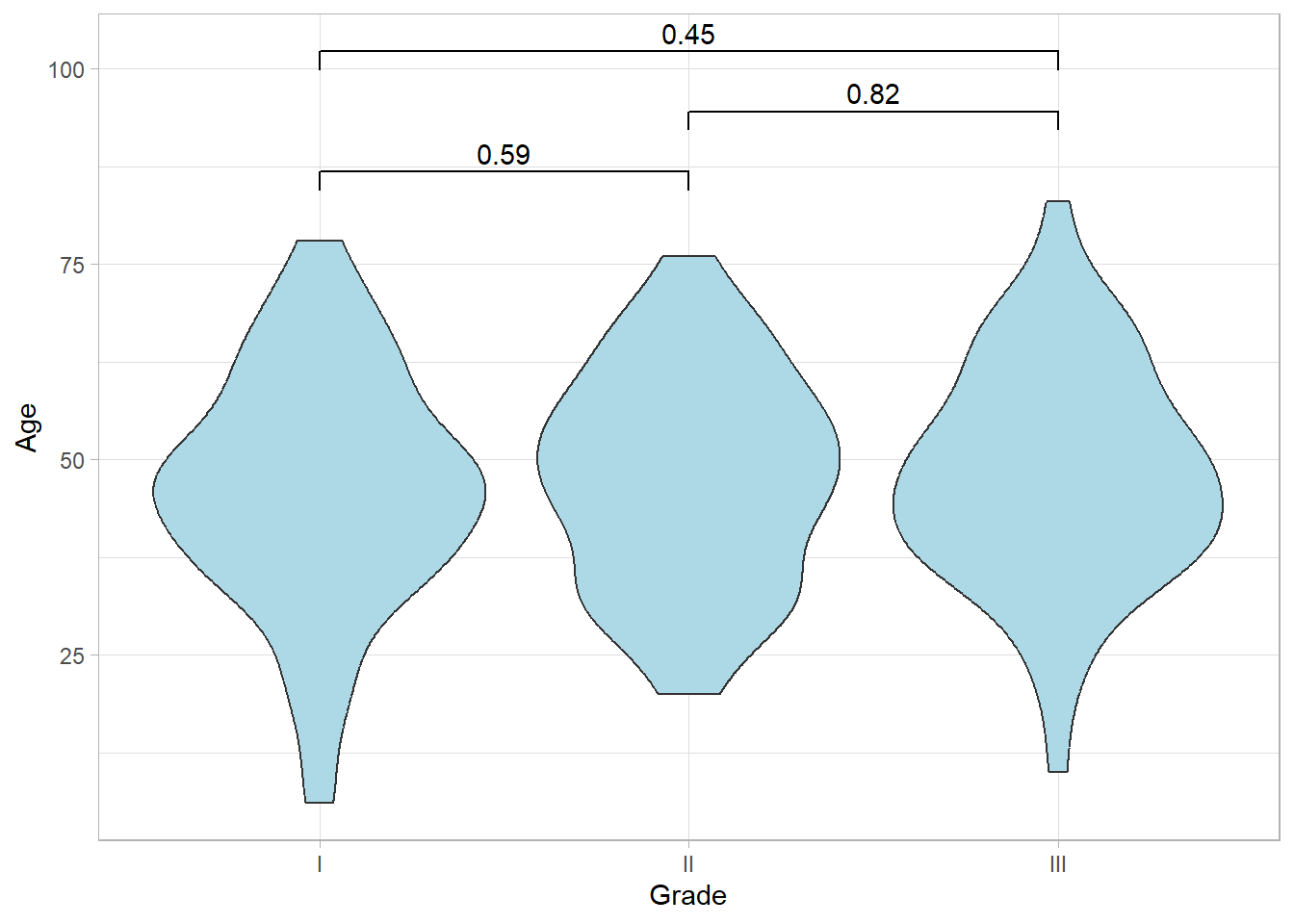
Alternativement, on peut utiliser un graphique en violons
qui représentent des courbes de densité dessinées en miroir.
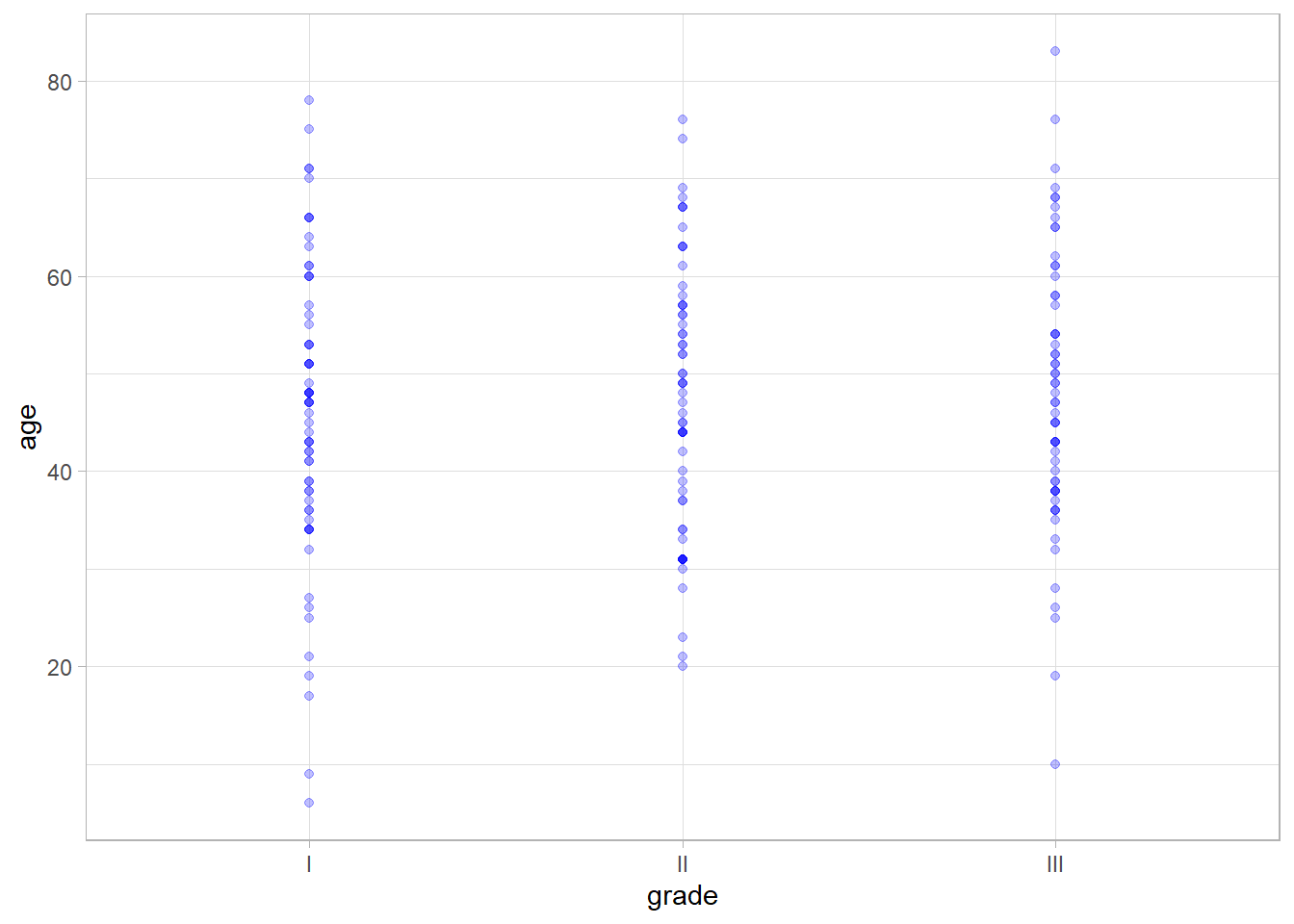
Il est toujours possible de représenter les observations individuelles sous la forme d’un nuage de points. Le paramètre alpha permet de rendre les points transparents afin de mieux visualiser les superpositions de points.
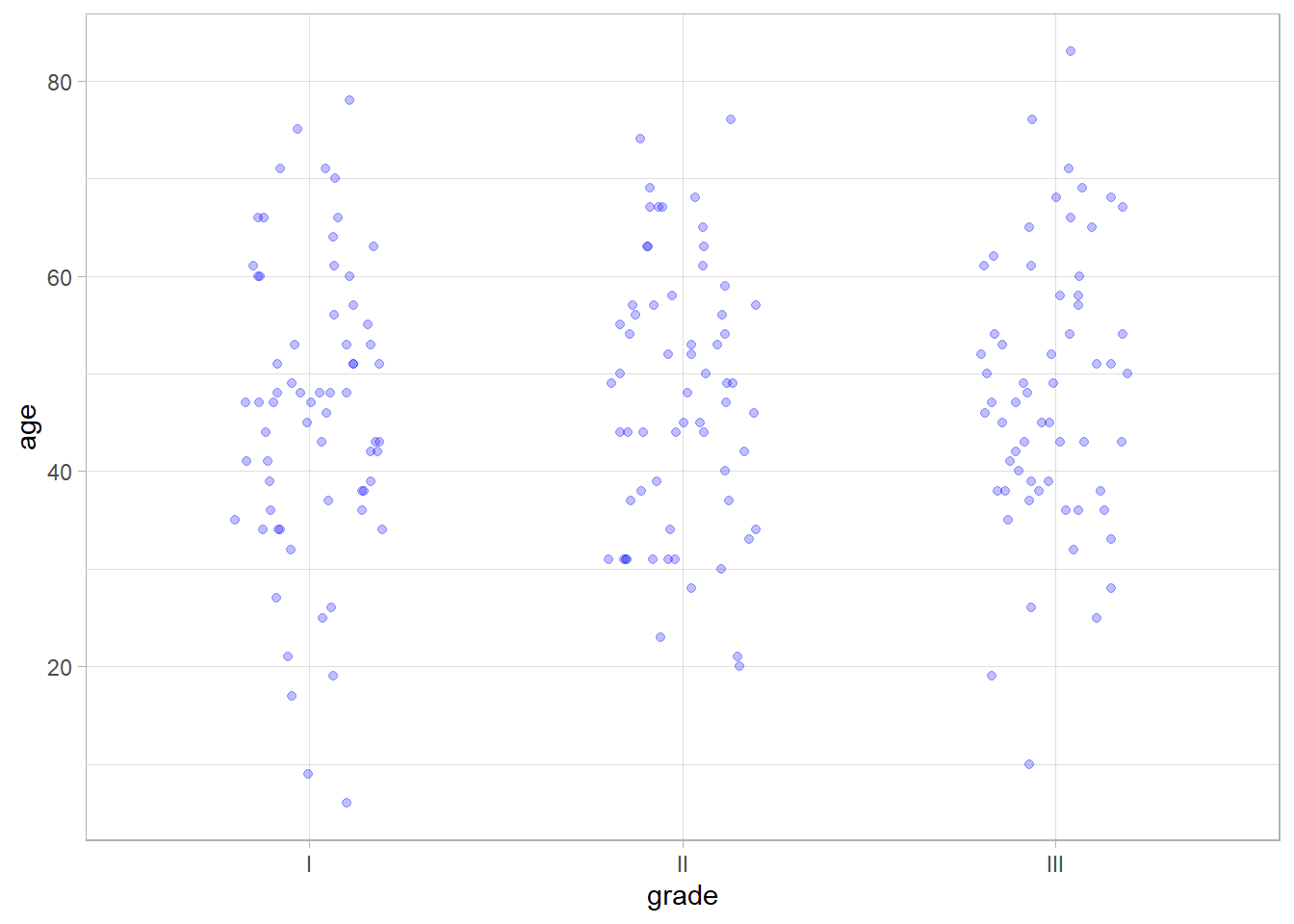
Comme la variable grade est catégorielle, tous les points d’une même modalité sont représentées sur une même ligne. La représentation peut être améliorée en ajoutant un décalage aléatoire sur l’axe horizontal. Cela s’obtient avec ggplot2::position_jitter() en précisant height = 0 pour ne pas ajouter de décalage vertical et width = .2 pour décaler horizontalement les points entre -20% et +20%.
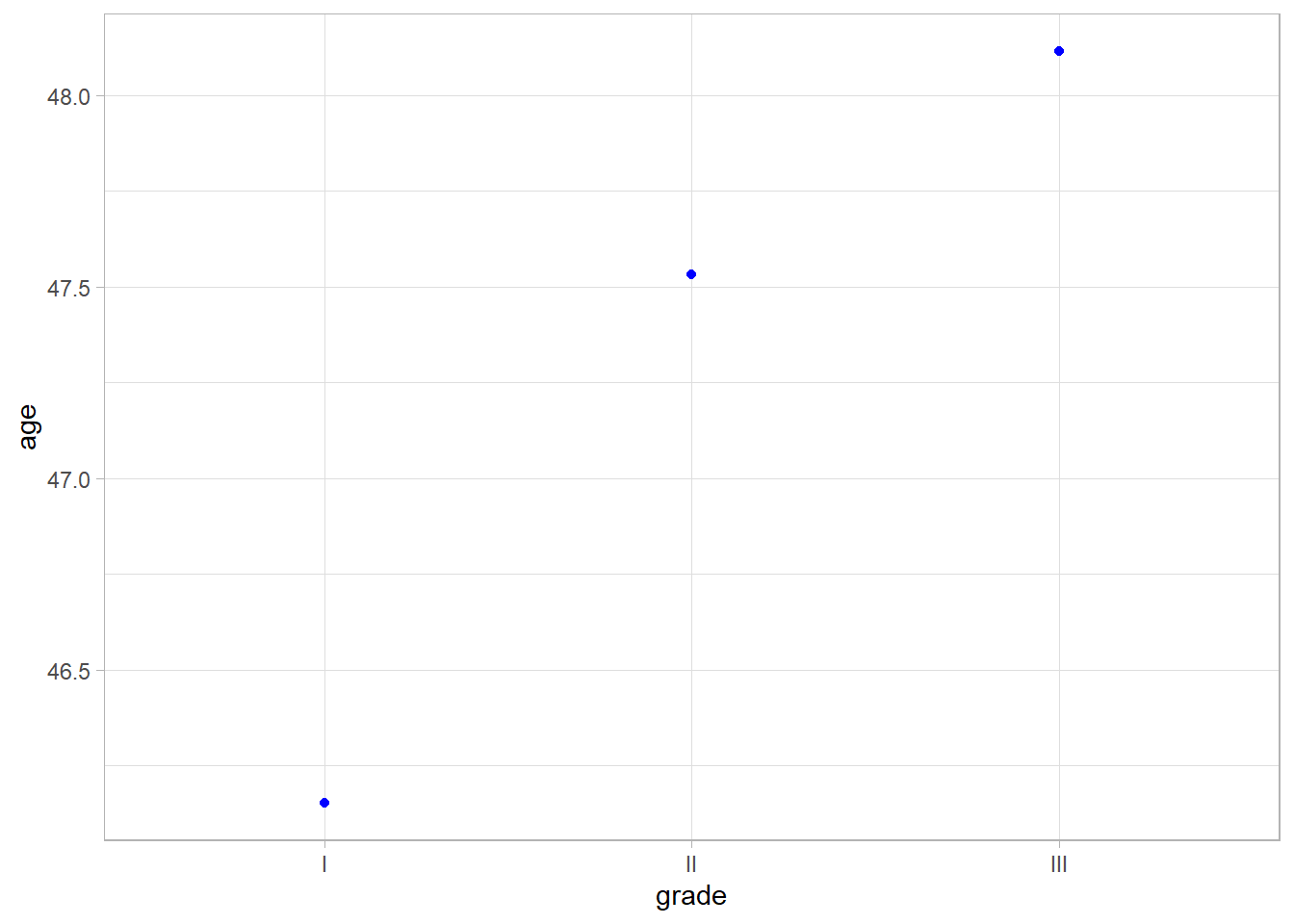
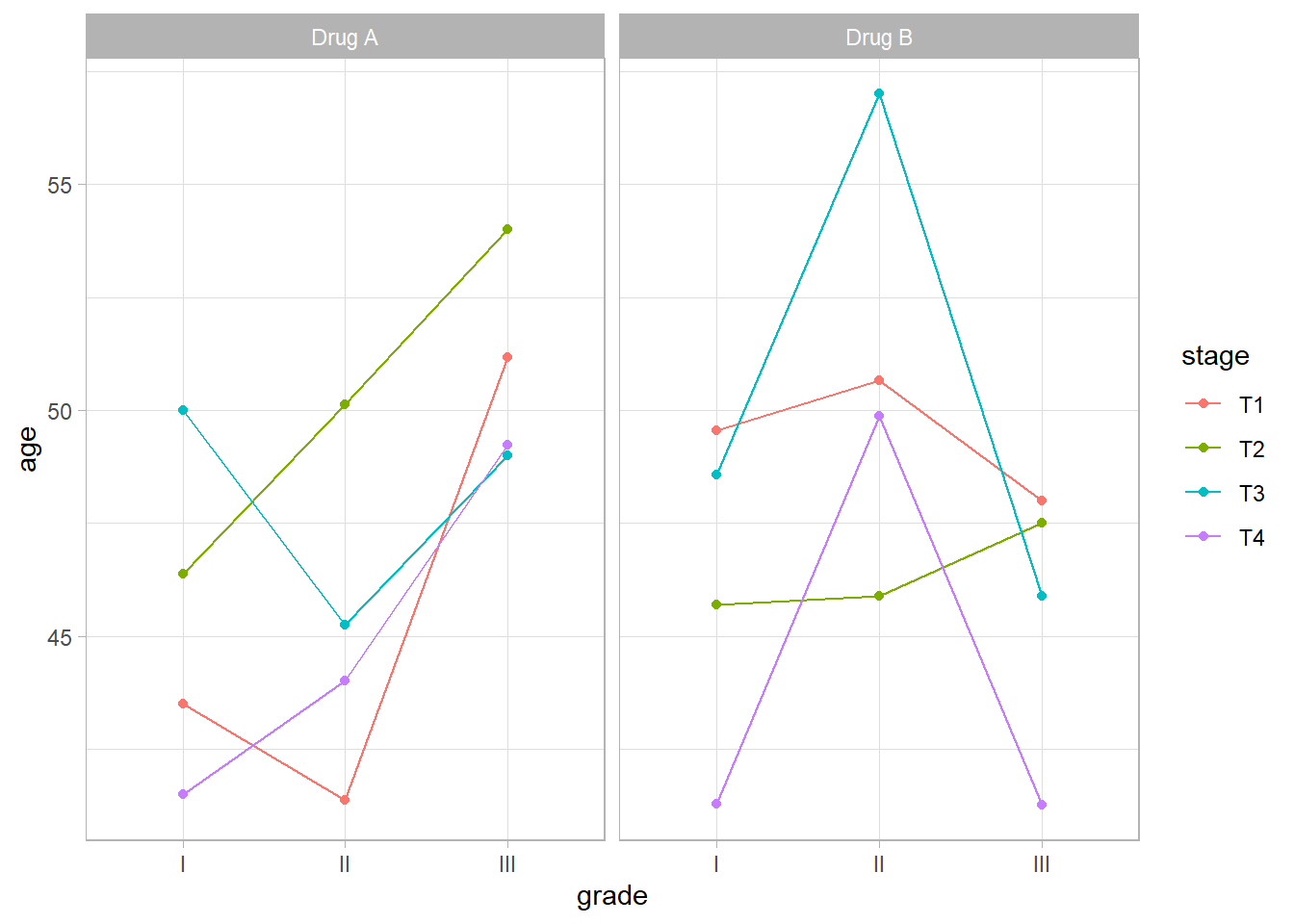
La statistique ggstats::stat_weighted_mean() de ggstats permets de calculer à la volée la moyenne du nuage de points.
Cela peut être utile pour effectuer des comparaisons multiples.
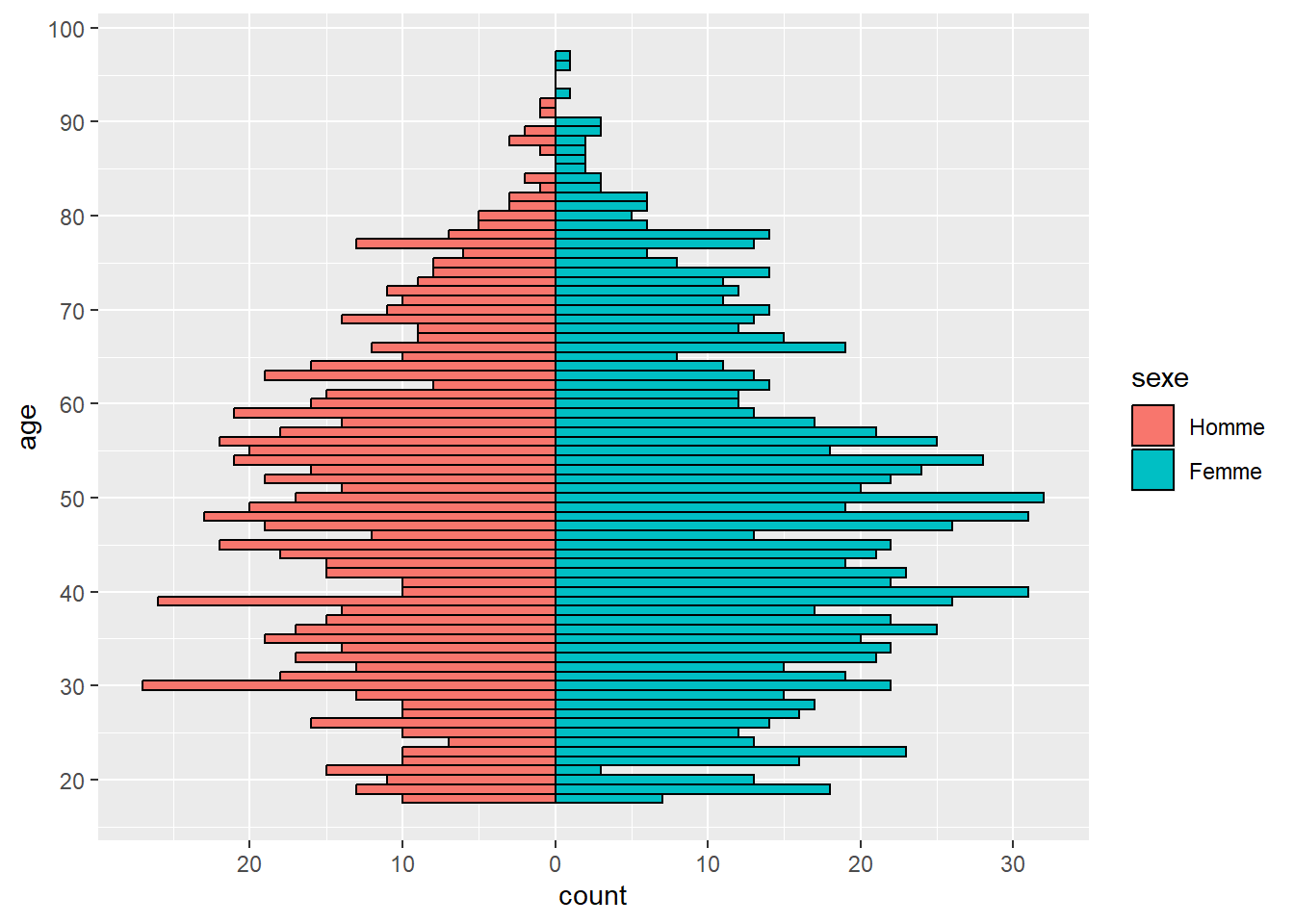
Il est possible de réaliser assez facilement une pyramide des âges en combinant un histogramme avec ggstats::position_diverging() fournie par le package ggstats.
Nous allons pour illustrer cela prendre le jeu de données hdv2003 fourni par le package questionr.
19.2.3 Représentations graphiques avec guideR
Similaire à guideR::plot_categorical(), le package guideR propose également une fonction guideR::plot_continuous() permettant de comparer une variable continue par sous-groupe à l’aide de boîtes à moustache.
Comme précédemment, un test de comparaison est réalisé : ici le test de Kruskal-Wallis qui sera présenté plus loin dans ce chapitre. Plusieurs options sont disponibles pour personnaliser le graphique.
Pour représenter alternativement des moyennes, avec leur intervalle de confiance et un test de comparaison de moyennes, on utilisera guideR::plot_means().
19.2.4 Calcul manuel
Le plus simple pour calculer des indicateurs par sous-groupe est d’avoir recours à dplyr::summarise() avec dplyr::group_by().
library(dplyr)
trial |>
group_by(grade) |>
summarise(
age_moy = mean(age, na.rm = TRUE),
age_med = median(age, na.rm = TRUE)
)# A tibble: 3 × 3
grade age_moy age_med
<fct> <dbl> <dbl>
1 I 46.2 47
2 II 47.5 48.5
3 III 48.1 47 On peut aussi utiliser directement les fonctions guideR::mean_sd() ou guidesR::median_iqr().
# A tibble: 3 × 8
x grade mean mean_low mean_high sd n missing
<chr> <fct> <dbl> <dbl> <dbl> <dbl> <int> <int>
1 age I 46.2 42.4 49.9 15.2 66 2
2 age II 47.5 44.1 51.0 13.7 62 6
3 age III 48.1 44.5 51.7 14.1 61 3# A tibble: 3 × 10
x grade median min q1 q3 max iqr n missing
<chr> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int> <int>
1 age I 47 6 37.2 55.8 78 18.5 66 2
2 age II 48.5 20 37 57 76 20 62 6
3 age III 47 10 38 58 83 20 61 3En base R, on peut avoir recours à tapply(). On lui indique d’abord le vecteur sur lequel on souhaite réaliser le calcul, puis un facteur qui indiquera les sous-groupes, puis une fonction qui sera appliquée à chaque sous-groupe et enfin, optionnellement, des arguments additionnels qui seront transmis à cette fonction.
19.2.5 Tests de comparaison
Pour comparer des moyennes ou des médianes, le plus facile est encore d’avoir recours à gtsummary et sa fonction gtsummary::add_p().
| Caractéristique |
I N = 681 |
II N = 681 |
III N = 641 |
p-valeur2 |
|---|---|---|---|---|
| Age | 47,0 (37,0, 56,0) | 48,5 (37,0, 57,0) | 47,0 (38,0, 58,0) | 0,8 |
| Manquant | 2 | 6 | 3 | |
| 1 Médiane (Q1, Q3) | ||||
| 2 Test de Kruskal-Wallis | ||||
Par défaut, pour les variables continues, un test de Kruskal-Wallis, calculé avec la fonction stats::kruskal.test(), est utilisé lorsqu’il y a trois groupes ou plus, et un test de Wilcoxon-Mann-Whitney, calculé avec stats::wilcox.test() (test de comparaison des rangs), lorsqu’il n’y a que deux groupes. Au sens strict, il ne s’agit pas de tests de comparaison des médianes mais de tests sur la somme des rangs2. En pratique, ces tests sont appropriés lorsque l’on présente les médianes et les intervalles inter-quartiles.
2 Si l’on a besoin spécifiquement d’un test de comparaison des médianes, il existe le test de Brown-Mood disponible dans le package coin avec la fonction coin::median_test(). Attention, il ne faut pas confondre ce test avec le test de dispersion de Mood implémenté dans la fonction stats::mood.test().
Si l’on affiche des moyennes, il serait plus juste d’utiliser un test t de Student (test de comparaison des moyennes) calculé avec stats::t.test(), valable seulement si l’on compare deux moyennes. Pour tester si trois moyennes ou plus sont égales, on aura plutôt recours à stats::oneway.test().
On peut indiquer à gtsummary::add_p() le test à utiliser avec le paramètre test.
trial |>
tbl_summary(
include = age,
by = grade,
statistic = all_continuous() ~ "{mean} ({sd})"
) |>
add_p(
test = all_continuous() ~ "oneway.test"
)| Caractéristique |
I N = 681 |
II N = 681 |
III N = 641 |
p-valeur2 |
|---|---|---|---|---|
| Age | 46,2 (15,2) | 47,5 (13,7) | 48,1 (14,1) | 0,7 |
| Manquant | 2 | 6 | 3 | |
| 1 Moyenne (ET) | ||||
| 2 One-way analysis of means (not assuming equal variances) | ||||
Classiquement, le test t de Student présuppose l’égalité des variances entre les deux sous-groupes, ce qui permet de former une estimation commune de la variance des deux échantillons (on parle de pooled variance), qui revient à une moyenne pondérée des variances estimées à partir des deux échantillons. Pour tester l’égalité des variances de deux échantillons, on peut utiliser stats::var.test().
Dans le cas où l’on souhaite relaxer cette hypothèse d’égalité des variances, le test de Welch ou la correction de Satterthwaite reposent sur l’idée que l’on utilise les deux estimations de variance séparément, suivie d’une approximation des degrés de liberté pour la somme de ces deux variances.
Par défaut, la fonction stats::t.test() réalise un test de Welch. Pour un test classique de Student, il faut lui préciser var.equal = TRUE.
De manière similaire, stats::oneway.test() ne présuppose pas, par défaut, l’égalité des variances et généralise donc le test de Welch au cas à trois modalités ou plus. Cependant, on peut là encore indiquer var.equal = TRUE, auquel cas une analyse de variance (ANOVA) classique sera réalisée, que l’on peut aussi obtenir avec stats::aov().
Il est possible d’indiquer à gtsummary::add_p() des arguments additionnels à passer à la fonction utilisée pour réaliser le test :
trial |>
tbl_summary(
include = age,
by = trt,
statistic = all_continuous() ~ "{mean} ({sd})"
) |>
add_p(
test = all_continuous() ~ "t.test",
test.args = all_continuous() ~ list(var.equal = TRUE)
)| Caractéristique |
Drug A N = 981 |
Drug B N = 1021 |
p-valeur2 |
|---|---|---|---|
| Age | 47,0 (14,7) | 47,4 (14,0) | 0,8 |
| Manquant | 7 | 4 | |
| 1 Moyenne (ET) | |||
| 2 Two Sample t-test | |||
La géométrie ggsignif::geom_signif() permet d’ajouter dynamiquement des tests de comparaison à un graphique. Par exemple :
19.2.6 Différence de deux moyennes
La fonctions gtsummary::add_difference() permet, pour une variable continue et si la variable catégorielle spécifiée via by n’a que deux modalités, de calculer la différence des deux moyennes, l’intervalle de confiance de cette différence et test si cette différence est significativement différente de 0 avec stats::t.test().
trial |>
tbl_summary(
include = age,
by = trt,
statistic = all_continuous() ~ "{mean} ({sd})"
) |>
add_difference()| Caractéristique |
Drug A N = 981 |
Drug B N = 1021 |
Différence2 | 95% IC2 | p-valeur2 |
|---|---|---|---|---|---|
| Age | 47,0 (14,7) | 47,4 (14,0) | -0,44 | -4,6 – 3,7 | 0,8 |
| Manquant | 7 | 4 | |||
| 1 Moyenne (ET) | |||||
| 2 test de Student | |||||
| Abréviation: IC = intervalle de confiance | |||||
19.3 Deux variables continues
19.3.1 Représentations graphiques
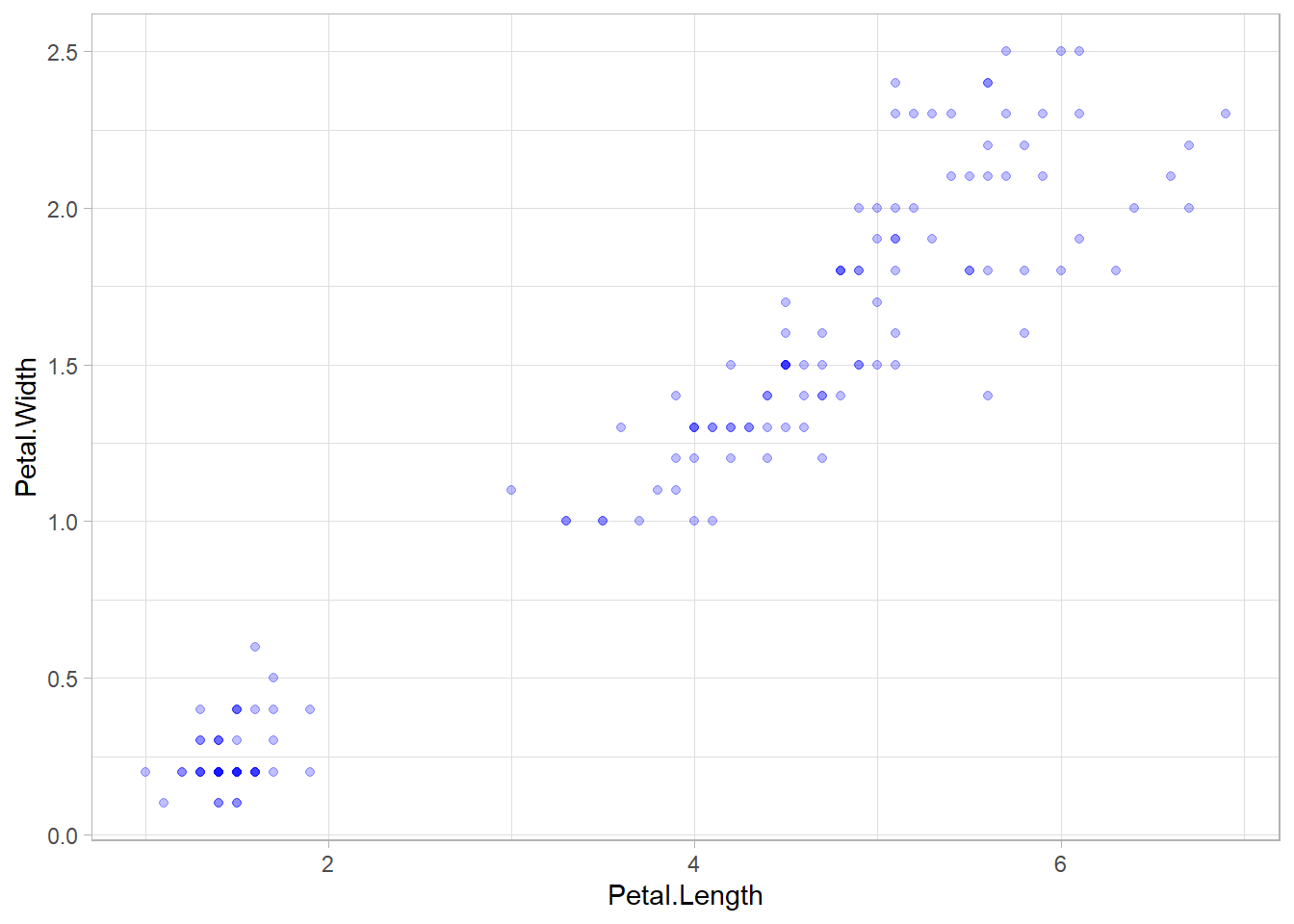
La comparaison de deux variables continues se fait en premier lieu graphique, en représentant, via un nuage de points, l’ensemble des couples de valeurs. Notez ici l’application d’un niveau de transparence (alpha) afin de faciliter la lecture des points superposés.
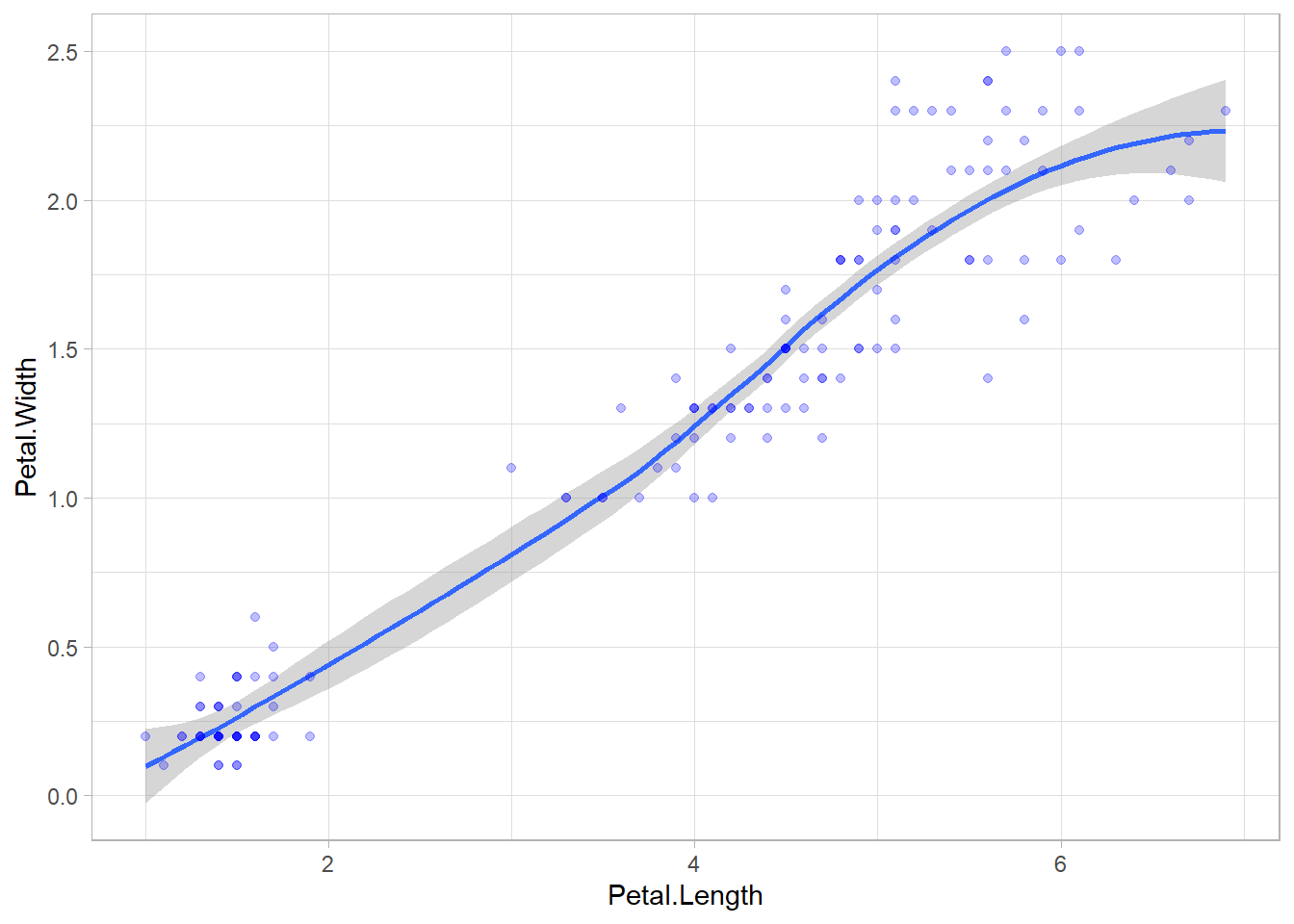
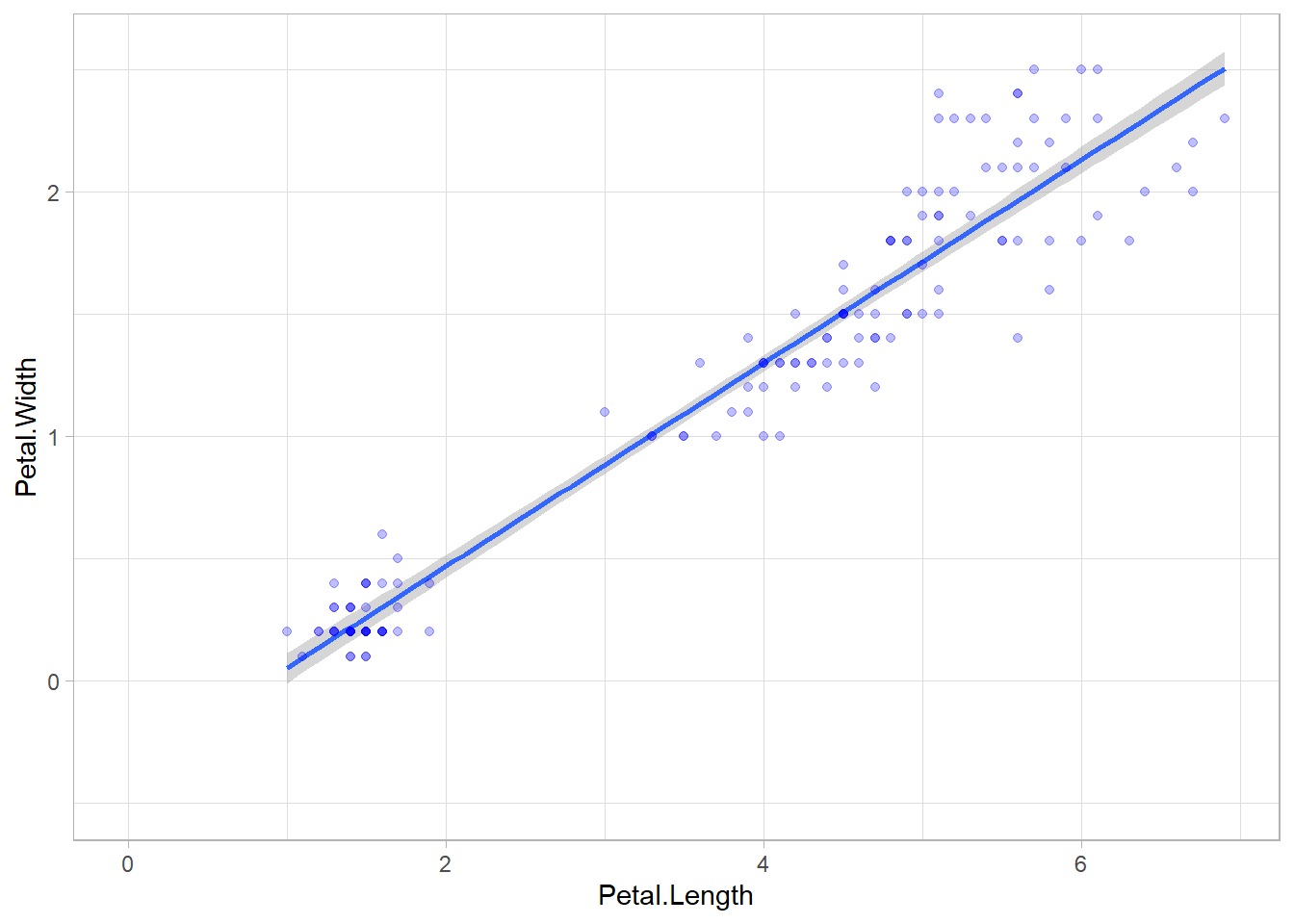
La géométrie ggplot2::geom_smooth() permets d’ajouter une courbe de tendance au graphique, avec son intervalle de confiance. Par défaut, il s’agit d’une régression polynomiale locale obtenue avec stats::loess().
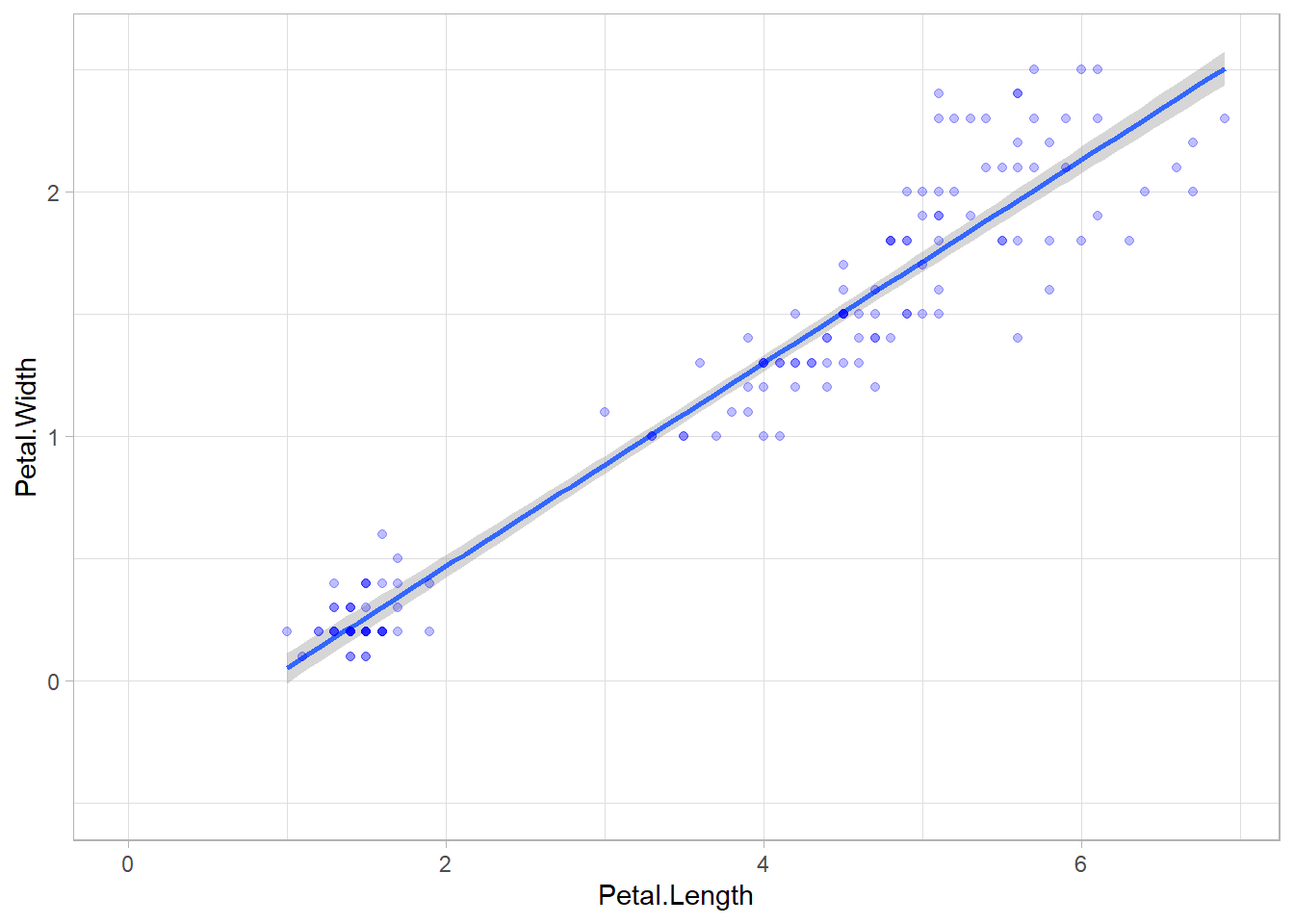
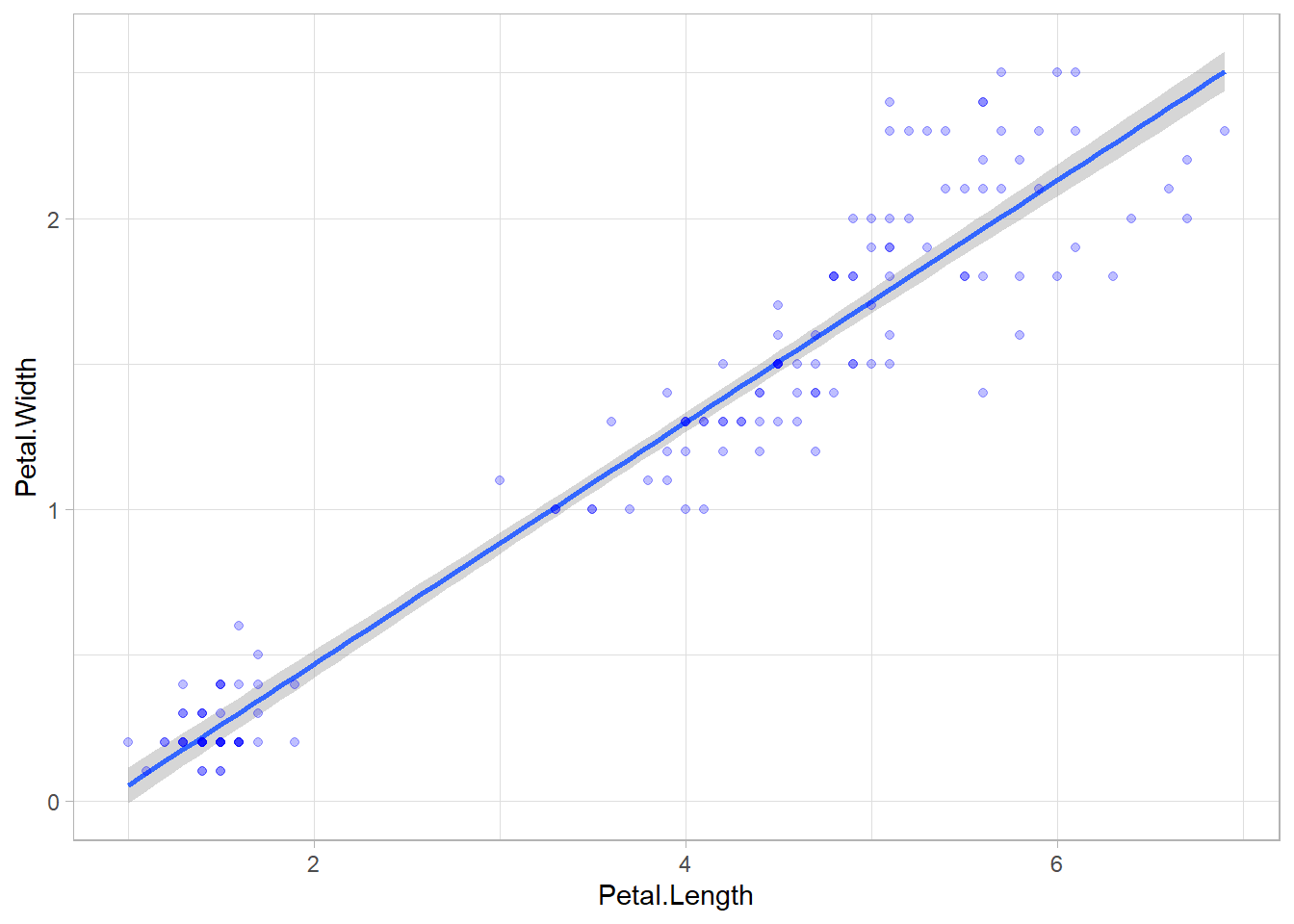
Pour afficher plutôt la droite de régression linéaire entre les deux variables, on précisera method = "lm".
Supposons que nous souhaitions montrer l’endroit où la droite de régression coupe l’axe des ordonnées (soit le point sur l’axe y pour x = 0).
Nous pouvons étendre la surface du graphique avec ggplot2::expand_limits(). Cependant, cela n’étend pas pour autant la droite de régression.
ggplot(iris) +
aes(x = Petal.Length, y = Petal.Width) +
geom_smooth(method = "lm") +
geom_point(colour = "blue", alpha = .25) +
theme_light() +
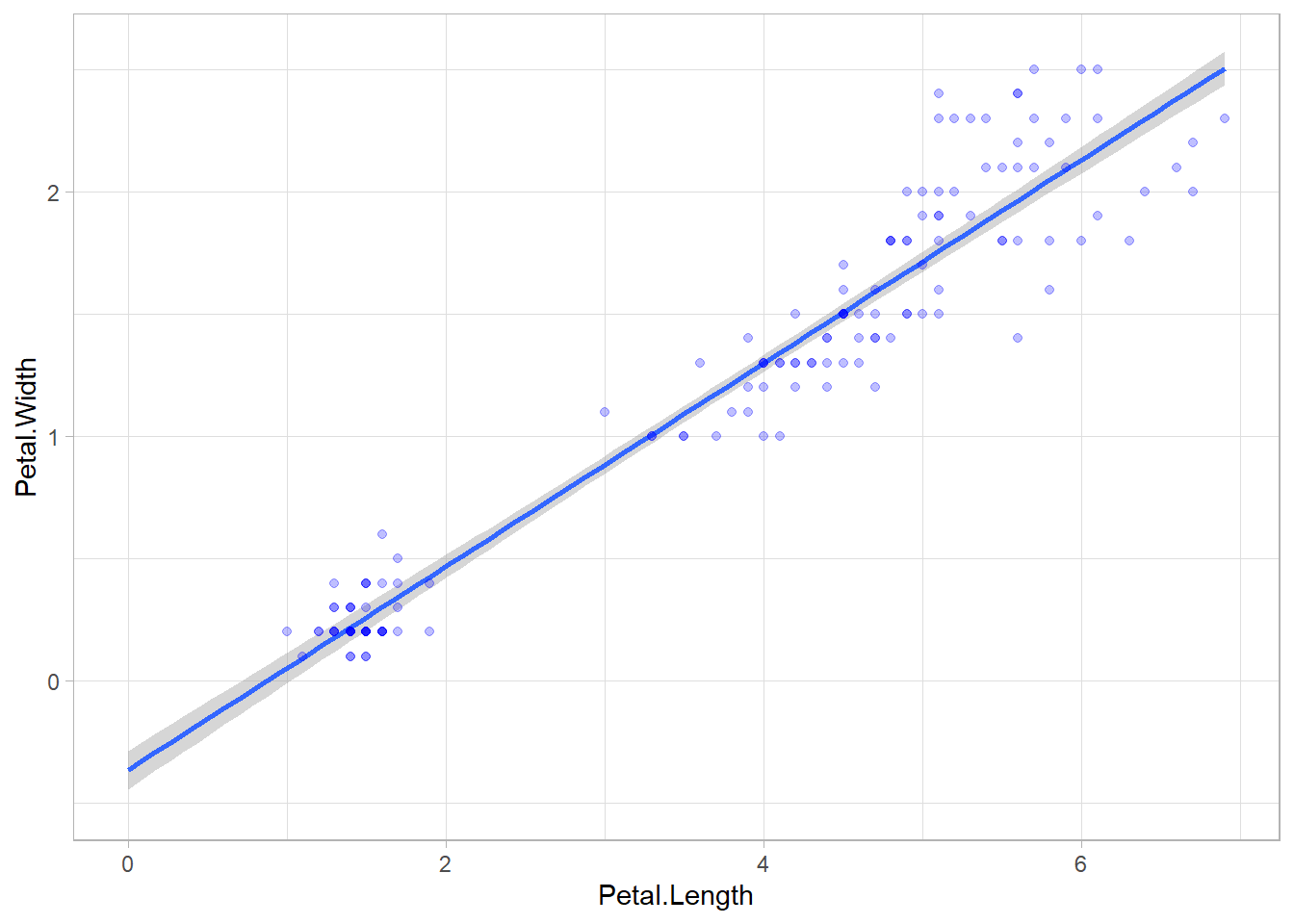
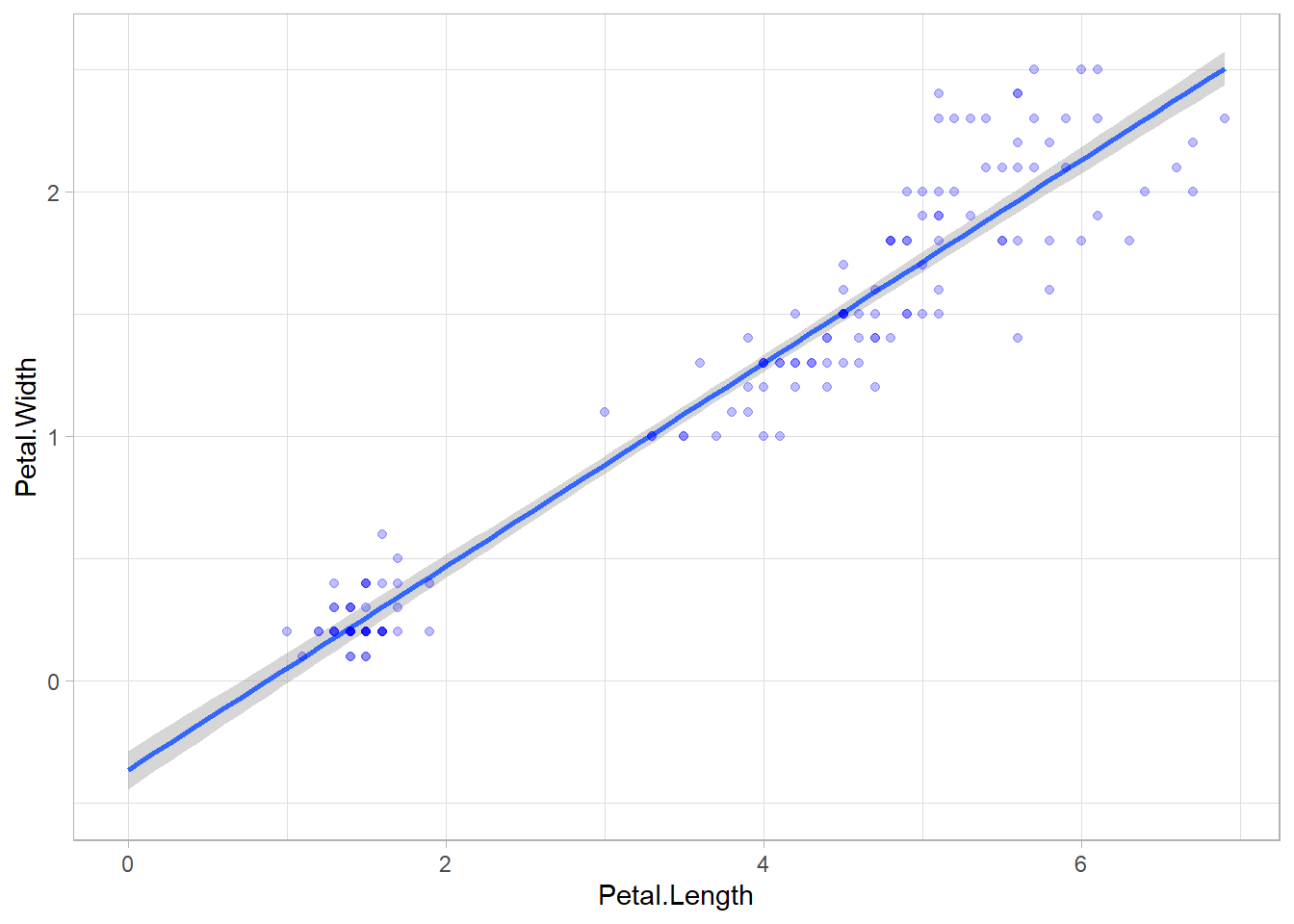
expand_limits(x = 0, y = -0.5)`geom_smooth()` using formula = 'y ~ x'Une solution simple consiste à utiliser l’option fullrange = TRUE dans ggplot2::geom_smooth() pour étendre la droite de régression à l’ensemble du graphique.
ggplot(iris) +
aes(x = Petal.Length, y = Petal.Width) +
geom_smooth(method = "lm", fullrange = TRUE) +
geom_point(colour = "blue", alpha = .25) +
theme_light() +
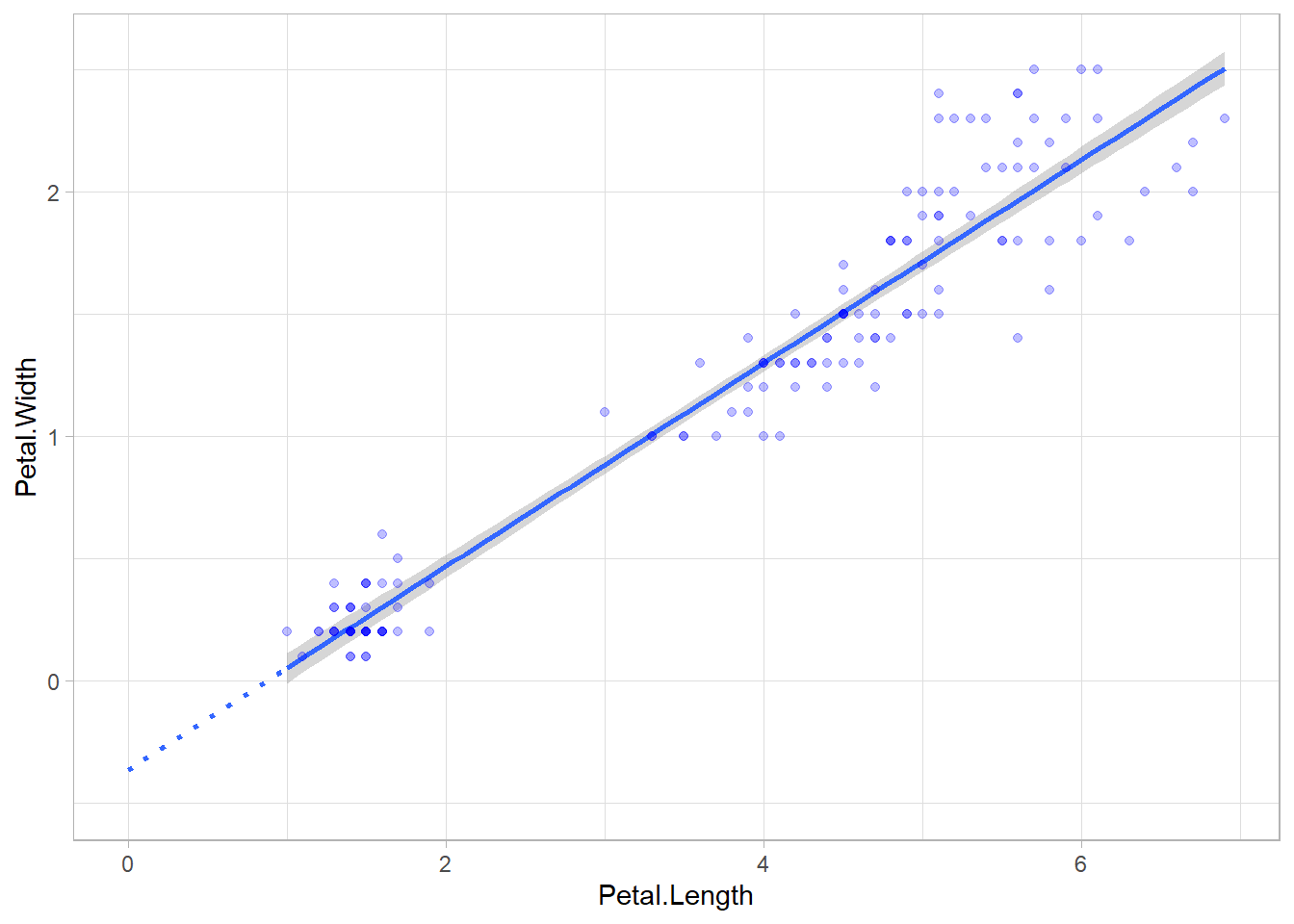
expand_limits(x = 0, y = -0.5)`geom_smooth()` using formula = 'y ~ x'On peut contrôler plus finement la partie de droite à afficher avec l’argument xseq (liste des valeurs pour lesquelles on prédit et affiche le lissage). On peut coupler deux appels à ggplot2::geom_smooth() pour afficher l’extension de la droite vers la gauche en pointillés. L’option se = FALSE permet de ne pas calculer d’intervalles de confiance pour ce second appel.
ggplot(iris) +
aes(x = Petal.Length, y = Petal.Width) +
geom_smooth(
method = "lm",
xseq = seq(0, 1, by = .1),
linetype = "dotted",
se = FALSE
) +
geom_smooth(method = "lm") +
geom_point(colour = "blue", alpha = .25) +
theme_light() +
expand_limits(x = 0, y = -0.5)`geom_smooth()` using formula = 'y ~ x'
`geom_smooth()` using formula = 'y ~ x'La géométrie ggplot2::geom_rug() permet d’afficher une représentation synthétique de la densité de chaque variable sur les deux axes.
19.3.2 Tester la relation entre les deux variables
Si l’on a besoin de calculer le coefficient de corrélation de Pearson entre deux variables, on aura recours à stats::cor().
Pour aller plus loin, on peut calculer une régression linéaire entre les deux variables avec stats::lm().
Call:
lm(formula = Petal.Length ~ Petal.Width, data = iris)
Residuals:
Min 1Q Median 3Q Max
-1.33542 -0.30347 -0.02955 0.25776 1.39453
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.08356 0.07297 14.85 <2e-16 ***
Petal.Width 2.22994 0.05140 43.39 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4782 on 148 degrees of freedom
Multiple R-squared: 0.9271, Adjusted R-squared: 0.9266
F-statistic: 1882 on 1 and 148 DF, p-value: < 2.2e-16Les résultats montrent une corrélation positive et significative entre les deux variables.
Pour une présentation propre des résultats de la régression linéaire, on utilisera gtsummary::tbl_regression(). La fonction gtsummary::add_glance_source_note() permet d’ajouter différentes statistiques en notes du tableau de résultats.
| Caractéristique | Beta | 95% IC | p-valeur |
|---|---|---|---|
| Petal.Width | 2,2 | 2,1 – 2,3 | <0,001 |
| Abréviation: IC = intervalle de confiance | |||
| R² = 0,927; Adjusted R² = 0,927; Sigma = 0,478; Statistique = 1 882; p-valeur = <0,001; df = 1; Log-likelihood = -101; AIC = 208; BIC = 217; Deviance = 33,8; degrés de liberté des résidus = 148; No. Obs. = 150 | |||
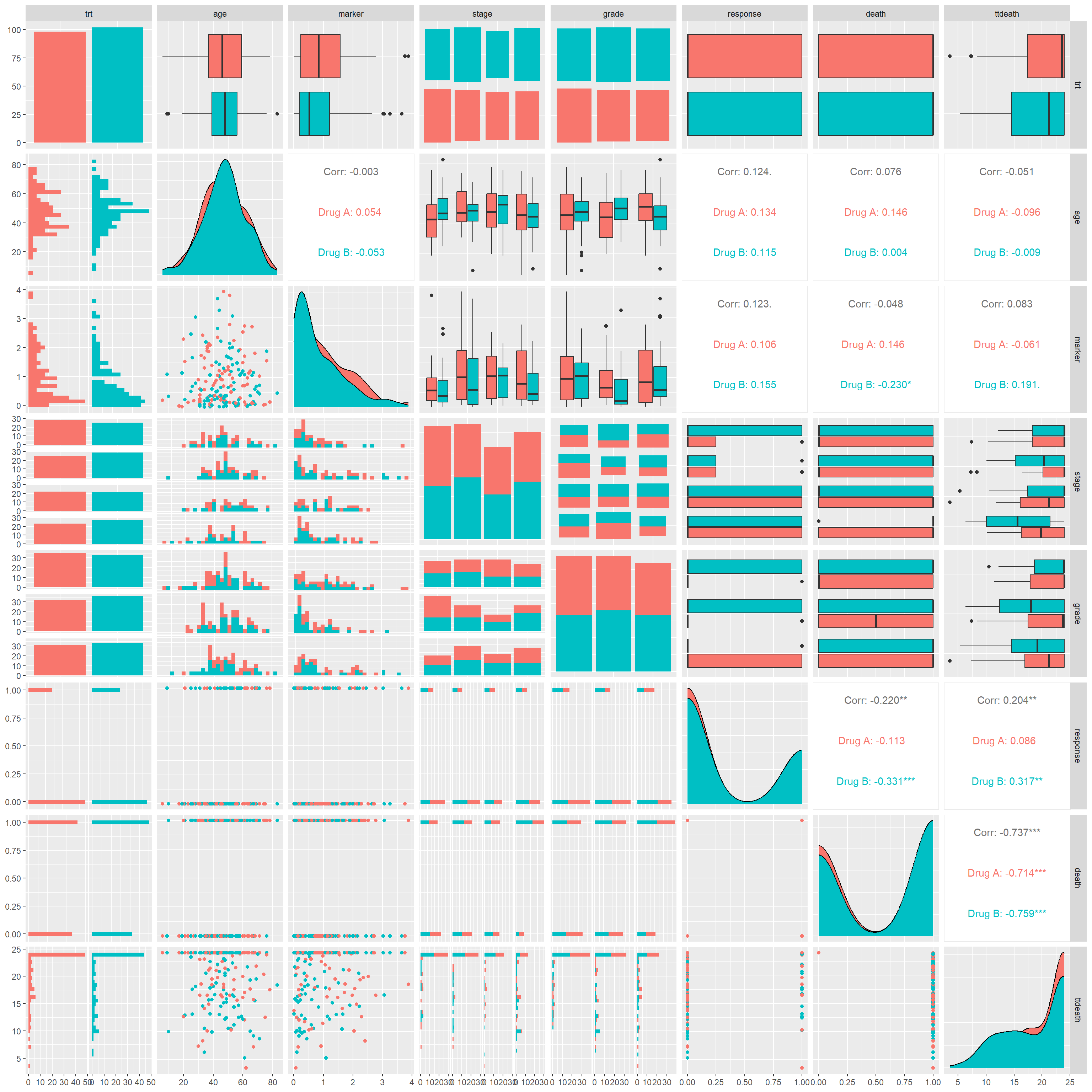
19.4 Matrice de corrélations
Le package GGally et sa fonction GGally::ggpairs() permettent de représenter facilement une matrice de corrélation entre plusieurs variables, tant quantitatives que qualitatives.
GGally::ggpairs() et sa petite sœur GGally::ggduo() offrent de nombreuses options de personnalisation qui sont détaillées sur le site dédié du package.
19.5 webin-R
La statistique univariée est présentée dans le webin-R #03 (statistiques descriptives avec gtsummary et esquisse) sur YouTube.
Les fonctions graphiques du package guideR sont présentées dans le webin-R #26 (Graphiques statistiques avec guideR) sur YouTube