41 Données longitudinales
Les données longitudinales permettent de suivre les individus au cours du temps. Leur collecte peut être prospective, dans le cadre d’une cohorte ou d’un observatoire de populations, ou rétrospective (par exemple dans le cadre d’enquêtes biographiques transversales).
Une des complexités des enquêtes longitudinales porte sur le fait que l’unité statistique n’est pas seulement l’individu. Une seconde unité statistique, le temps, est également à prendre en compte. Il convient d’être vigilant sur l’éventuel pas de temps utilisé pour la collecte (dates exactes, mois, années…) ainsi que sur l’horloge / le calendrier utilisé, définis en fonction d’un évènement origine : âge de l’individu (et donc durée depuis la naissance), durée depuis le diagnostic (par exemple dans une cohorte clinique), durée en union (donc depuis la mise en union)…
Il est également essentiel de bien distinguer les évènements qui ont lieu à un point dans le temps et le statut ou l’état d’un individu, qui a lieu sur une période de temps. Un évènement peut modifier le statut d’un individu. Par exemples, les mariages et les divorces sont des évènements modifiant le statut matrimonial.
41.1 Différents formats de données
Pour représenter l’évolution d’une ou plusieurs variables au cours du temps, plusieurs formats peuvent être utilisés.
On parle de format large lorsque le jeu de données contient une seule ligne par individu, les évolutions d’une dimension au cours du temps étant codées avec une variable par pas de temps. Par exemple, dans le cadre d’une enquête sur les unions, le statut matrimonial pourrait être codés avec une variable pour coder la situation matrimonial à chaque âge : smat20 pour le statut matrimonial à 20 ans, smat21 à 21 ans, smat22 à 22 ans, etc.
Ce format est couramment utilisé par les producteurs de données dans les grandes enquêtes, car il permet de stocker l’information dans une seule grande table de données, avec les autres variables du questionnaire. C’est également le format de données attendues par certains package, par exemple TraMineR dans le cadre d’une analyse de séquences (cf. Chapitre 45).
Il présente néanmoins plusieurs inconvénients. Comme indiqué dans le chapitre sur les tibbles (cf. Section 5.1), les données ne sont pas au format tidy, notamment car une même information (ici le statut matrimonial) est stockées dans plusieurs colonnes et car une seconde information (ici l’âge) est stockée dans l’intitulé des variables et non dans une variable en tant que telle. Le format large n’est pas très adapté pour du recodage ou encore pour le calcul d’indicateurs (par exemple l’âge au premier mariage). Ce n’est pas non plus un format adapté pour la production de graphiques avec ggplot2, de tableaux avec gtsummary ou la réalisation de modèles à observations répétées.
Pour une représentation tydy des données, on optera pour un format long : chaque correspondra à un individu et à un pas de temps donné. Nous aurons donc une ligne pour le statut matrimonial à 20 ans, une ligne pour celui à 21 ans, etc. Dans un telle table de données, où l’unité statistique est la personne-temps, il aura donc une variable pour stocker la dimension temporelle et une autre pour le statut de l’individu. Un tel format est particulièrement adapté pour facilement représenter simultanément plusieurs dimensions de l’individu, mais également pour considérer différentes horloges. Nous verrons quelques exemples plus loin.
Enfin, les données peuvent également être représentés dans un format périodique. Alors que dans un format long chaque ligne représente un pas de temps et a, de fait, la même durée, dans un format périodique chaque ligne représente une période de temps où les autres variables sont identiques. Il est donc nécessaire dans ce cas de disposer deux deux variables temporelles : l’une indiquant le début et la seconde la fin de la période considérée. Ce type de format est notamment attendu par survival pour la réalisation d’une analyse de survie (cf. Chapitre 44) avec prise en compte de facteurs variant dans le temps.
41.2 Passage d’un format à l’autre
Prenons un exemple concret pour illustrer notre propos et voir comment passer d’un format à un autre.
Le package seqhandbook fournit un jeu de données seqhandbook::seqmsa correspondant aux trajectoires matrimoniales, parentales et résidentielles entre 14 et 35 ans de 500 personnes interrogées dans le cadre de l’enquête Biographies et entourage de l’Ined en 2001.
Jetons un œil aux données.
── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.6
✔ forcats 1.0.1 ✔ stringr 1.6.0
✔ ggplot2 4.0.1 ✔ tibble 3.3.0
✔ lubridate 1.9.4 ✔ tidyr 1.3.1
✔ purrr 1.2.0
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorsRows: 500
Columns: 66
$ slog14 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, …
$ slog15 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, …
$ slog16 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, …
$ slog17 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, …
$ slog18 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, …
$ slog19 <dbl> 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, …
$ slog20 <dbl> 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, …
$ slog21 <dbl> 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, …
$ slog22 <dbl> 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, …
$ slog23 <dbl> 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, …
$ slog24 <dbl> 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, …
$ slog25 <dbl> 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, …
$ slog26 <dbl> 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, …
$ slog27 <dbl> 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, …
$ slog28 <dbl> 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, …
$ slog29 <dbl> 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, …
$ slog30 <dbl> 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, …
$ slog31 <dbl> 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ slog32 <dbl> 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ slog33 <dbl> 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ slog34 <dbl> 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ slog35 <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ smat14 <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ smat15 <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ smat16 <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ smat17 <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ smat18 <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ smat19 <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 1, 1, 1, …
$ smat20 <dbl> 1, 3, 1, 1, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 1, 1, 1, …
$ smat21 <dbl> 1, 3, 1, 1, 3, 3, 1, 3, 1, 1, 1, 1, 3, 3, 1, 1, 1, 3, 2, 1, 1, …
$ smat22 <dbl> 1, 3, 1, 3, 3, 3, 1, 3, 1, 1, 1, 1, 3, 3, 1, 1, 1, 3, 2, 1, 1, …
$ smat23 <dbl> 1, 3, 1, 3, 3, 3, 1, 3, 1, 1, 1, 1, 3, 3, 1, 1, 1, 3, 2, 1, 1, …
$ smat24 <dbl> 1, 3, 1, 3, 3, 3, 1, 3, 1, 1, 1, 3, 3, 3, 1, 1, 1, 3, 3, 1, 1, …
$ smat25 <dbl> 1, 3, 3, 3, 3, 3, 1, 3, 2, 1, 1, 3, 3, 3, 1, 1, 1, 3, 3, 1, 1, …
$ smat26 <dbl> 2, 3, 3, 3, 3, 3, 1, 3, 2, 1, 1, 3, 3, 3, 1, 1, 1, 3, 3, 1, 1, …
$ smat27 <dbl> 2, 3, 3, 3, 3, 3, 1, 3, 2, 1, 1, 3, 3, 3, 1, 1, 1, 3, 3, 1, 1, …
$ smat28 <dbl> 2, 3, 3, 3, 3, 3, 1, 3, 3, 1, 1, 3, 3, 3, 1, 2, 1, 3, 3, 1, 1, …
$ smat29 <dbl> 2, 3, 3, 3, 3, 3, 1, 3, 3, 1, 1, 3, 3, 3, 1, 2, 2, 3, 3, 1, 1, …
$ smat30 <dbl> 2, 3, 3, 3, 3, 3, 1, 3, 3, 1, 1, 3, 3, 3, 1, 2, 3, 3, 3, 1, 3, …
$ smat31 <dbl> 3, 3, 3, 3, 3, 3, 1, 3, 3, 1, 1, 3, 3, 3, 1, 2, 3, 3, 3, 1, 3, …
$ smat32 <dbl> 3, 3, 3, 3, 2, 3, 1, 3, 3, 1, 1, 3, 3, 3, 1, 2, 3, 3, 3, 1, 3, …
$ smat33 <dbl> 3, 3, 3, 3, 2, 3, 3, 3, 3, 1, 3, 3, 3, 3, 1, 2, 3, 3, 3, 1, 3, …
$ smat34 <dbl> 3, 3, 3, 3, 2, 3, 3, 3, 3, 1, 3, 3, 3, 3, 1, 2, 3, 3, 3, 3, 3, …
$ smat35 <dbl> 3, 3, 3, 3, 2, 3, 3, 3, 3, 1, 3, 3, 3, 3, 1, 2, 3, 3, 3, 3, 3, …
$ nenf14 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ nenf15 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ nenf16 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ nenf17 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, …
$ nenf18 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, …
$ nenf19 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, …
$ nenf20 <dbl> 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, …
$ nenf21 <dbl> 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 1, 0, 1, 0, 0, 0, …
$ nenf22 <dbl> 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 3, 1, 0, 1, 0, 1, 0, 0, 0, …
$ nenf23 <dbl> 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 3, 1, 0, 1, 0, 1, 0, 0, 0, …
$ nenf24 <dbl> 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 3, 1, 0, 1, 0, 2, 0, 0, 0, …
$ nenf25 <dbl> 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 3, 1, 0, 1, 0, 2, 0, 0, 0, …
$ nenf26 <dbl> 0, 1, 0, 1, 1, 1, 0, 1, 2, 0, 0, 0, 3, 1, 0, 1, 0, 2, 1, 0, 0, …
$ nenf27 <dbl> 0, 1, 0, 1, 1, 1, 0, 1, 2, 0, 0, 1, 3, 1, 0, 1, 0, 2, 1, 0, 0, …
$ nenf28 <dbl> 0, 1, 1, 1, 1, 1, 0, 2, 3, 0, 0, 1, 3, 1, 0, 1, 0, 2, 1, 0, 0, …
$ nenf29 <dbl> 0, 2, 1, 2, 1, 1, 0, 2, 3, 0, 0, 2, 3, 1, 0, 1, 0, 2, 1, 0, 0, …
$ nenf30 <dbl> 0, 2, 2, 2, 1, 1, 0, 3, 3, 0, 0, 2, 3, 1, 0, 1, 0, 2, 2, 0, 0, …
$ nenf31 <dbl> 1, 2, 2, 2, 1, 1, 0, 3, 3, 0, 0, 2, 3, 1, 0, 1, 1, 2, 2, 0, 1, …
$ nenf32 <dbl> 1, 2, 2, 2, 1, 1, 0, 3, 3, 0, 0, 2, 3, 1, 0, 1, 1, 2, 2, 0, 1, …
$ nenf33 <dbl> 1, 2, 2, 2, 2, 1, 0, 3, 3, 0, 0, 2, 3, 1, 0, 1, 2, 2, 2, 0, 1, …
$ nenf34 <dbl> 1, 2, 2, 2, 2, 1, 0, 3, 3, 0, 1, 2, 3, 1, 0, 1, 2, 2, 2, 0, 2, …
$ nenf35 <dbl> 1, 2, 2, 2, 2, 1, 0, 3, 3, 0, 2, 2, 3, 1, 0, 1, 2, 2, 2, 1, 2, …Ce jeu de données comporte 66 variables :
- les variables slog14 à slog35 correspondent au statut résidentiel à chaque âge ;
- les variables smat14 à smat35 au statut matrimonial ;
- les variables nenf14 à nenf35 au nombre d’enfants.
Chaque variable est ici codée sous forme numérique.
On peut noter l’absence d’identifiant individu. Commençons donc pas en créer un.
Pour passer à un format long, nous allons utiliser tidyr::pivot_longer() que nous avons déjà évoquée dans le chapitre consacré à tidyr (cf. Chapitre 37). Nous allons devoir traiter chaque dimension séparément avant de les fusionner avec dplyr::full_join().
slog <-
dlarge |>
select(id_ind, starts_with("slog")) |>
pivot_longer(
cols = starts_with("slog"),
values_to = "slog",
names_to = "age",
names_prefix = "slog"
)
smat <-
dlarge |>
select(id_ind, starts_with("smat")) |>
pivot_longer(
cols = starts_with("smat"),
values_to = "smat",
names_to = "age",
names_prefix = "smat"
)
nenf <-
dlarge |>
select(id_ind, starts_with("nenf")) |>
pivot_longer(
cols = starts_with("nenf"),
values_to = "nenf",
names_to = "age",
names_prefix = "nenf"
)
dlong <-
slog |>
full_join(smat, by = c("id_ind", "age")) |>
full_join(nenf, by = c("id_ind", "age")) |>
mutate(age = as.integer(age))Il est maintenant aisé de documenter nos données avec labelled. Nous allons utiliser labelled::set_value_labels() pour définir des étiquettes de valeurs puis labelled::unlabelled() pour convertir les trois variables de statut en facteurs (cf. Chapitre 12).
library(labelled)
dlong <-
dlong |>
set_variable_labels(
age = "Âge",
slog = "Statut résidentiel",
smat = "Statut matrimonial",
nenf = "Statut parental"
) |>
set_value_labels(
slog = c(
"non indépendant" = 0,
"logement indépendant" = 1
),
smat = c(
"jamais en union" = 1,
"union cohabitante" = 2,
"marié·e" = 3,
"séparé·e" = 4
),
nenf = c(
"sans enfant" = 0,
"1 enfant" = 1,
"2 enfants" = 2,
"3 enfants ou +" = 3
)
) |>
unlabelled()Voyons maintenant à quoi ressemble notre fichier long :
# A tibble: 11,000 × 5
id_ind age slog smat nenf
<int> <int> <fct> <fct> <fct>
1 1 14 non indépendant jamais en union sans enfant
2 1 15 non indépendant jamais en union sans enfant
3 1 16 non indépendant jamais en union sans enfant
4 1 17 non indépendant jamais en union sans enfant
5 1 18 non indépendant jamais en union sans enfant
6 1 19 non indépendant jamais en union sans enfant
7 1 20 non indépendant jamais en union sans enfant
8 1 21 non indépendant jamais en union sans enfant
9 1 22 non indépendant jamais en union sans enfant
10 1 23 non indépendant jamais en union sans enfant
# ℹ 10,990 more rowsLe passage d’un format long à un format périodique est souvent un peu plus complexe, car cela nécessite d’identifier les successions de lignes identiques puis de les regrouper en retenant l’âge du début et l’âge de la fin de la période. Dans ce cadre, les fonctions guideR::cumdifferent() et guideR::num_cycle() que nous avons abordé dans le chapitre sur les fonctions à fenêtre peuvent être utiles (cf. Section 39.4). Heureusement, guideR, le package compagnon de guide-R, propose une fonction guideR::long_to_periods() justement dédiée à la conversion d’un format long à un format périodique.
La première chose est de bien définir les variables à prendre en compte pour l’identification des périodes. En effet, cela impactera sur le nombre de périodes obtenues. Si l’on se contente d’indiquer un identifiant individuel et une variable temporelle, alors le résultat n’inclura qu’une période par individu en renverra le premier âge et le dernier âge connu.
# A tibble: 500 × 3
# Groups: id_ind [500]
id_ind age .stop
<int> <int> <int>
1 1 14 35
2 2 14 35
3 3 14 35
4 4 14 35
5 5 14 35
6 6 14 35
7 7 14 35
8 8 14 35
9 9 14 35
10 10 14 35
# ℹ 490 more rowsSi je passe la variable slog au paramètre by, alors une nouvelle période sera créée à chaque fois que le statut résidentiel change.
# A tibble: 1,131 × 4
# Groups: id_ind [500]
id_ind age .stop slog
<int> <int> <int> <fct>
1 1 14 26 non indépendant
2 1 26 35 logement indépendant
3 2 14 22 non indépendant
4 2 22 35 logement indépendant
5 3 14 25 non indépendant
6 3 25 35 logement indépendant
7 4 14 22 non indépendant
8 4 22 35 logement indépendant
9 5 14 20 non indépendant
10 5 20 35 logement indépendant
# ℹ 1,121 more rowsNous pouvons ainsi voir que l’individu n’avait pas de logement indépendant de l’âge de 14 à 26 ans puis a eu un logement indépendant de 26 à 35 ans.
Si l’on passe plusieurs variables à by, alors une nouvelle période sera créée à chaque changement d’une de ces variables.
# A tibble: 2,203 × 6
# Groups: id_ind [500]
id_ind age .stop slog smat nenf
<int> <int> <int> <fct> <fct> <fct>
1 1 14 26 non indépendant jamais en union sans enfant
2 1 26 31 logement indépendant union cohabitante sans enfant
3 1 31 35 logement indépendant marié·e 1 enfant
4 2 14 20 non indépendant jamais en union sans enfant
5 2 20 21 non indépendant marié·e sans enfant
6 2 21 22 non indépendant marié·e 1 enfant
7 2 22 29 logement indépendant marié·e 1 enfant
8 2 29 35 logement indépendant marié·e 2 enfants
9 3 14 25 non indépendant jamais en union sans enfant
10 3 25 28 logement indépendant marié·e sans enfant
# ℹ 2,193 more rowsPour repasser d’un format long à un format large, on aura recours à tidyr::pivot_wider() et pour le passage d’un format périodique à un format long à guideR::periods_to_long().
41.3 Exemples de visualisation et de manipulation
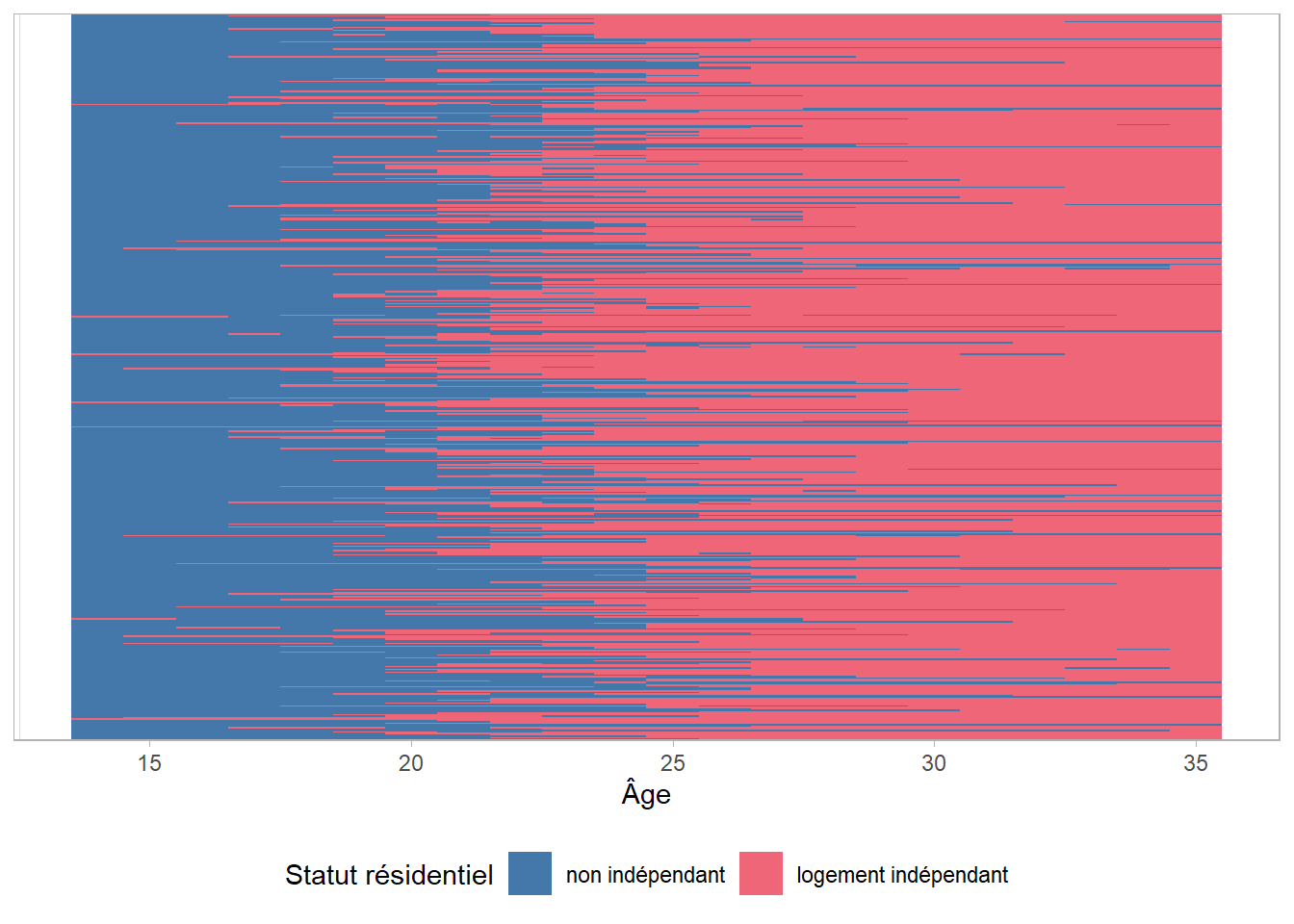
Pour visualiser rapidement les trajectoires individuelles, guideR propose une fonction guideR::plot_trajectories() qui part d’une table de données au format long. On parle de tapis de séquences. Par exemple, pour les trajectoires résidentielles selon l’âge.
Chaque ligne repésente un individu et sa trajectoire individuelle selon la ligne de temps (ici l’âge).
Nous pouvons nous demander s’il y a un lien entre l’entrée en union et le statut résidentiel.
Première étape, calculons, pour chaque individu, l’âge de première entrée en union. Il s’agit donc du plus petit âge ou le statut matrimonial est différent de jamais en union
. Cela est relativement facile avec un format long et les verbes de dplyr.
age_1u <-
dlong |>
filter(smat != "jamais en union") |>
group_by(id_ind) |>
summarise(age_1u = min(age)) |>
set_variable_labels(
age_1u = "Âge à la première union"
)
age_1u# A tibble: 459 × 2
id_ind age_1u
<int> <int>
1 1 26
2 2 20
3 3 25
4 4 22
5 5 20
6 6 21
7 7 33
8 8 21
9 9 25
10 11 33
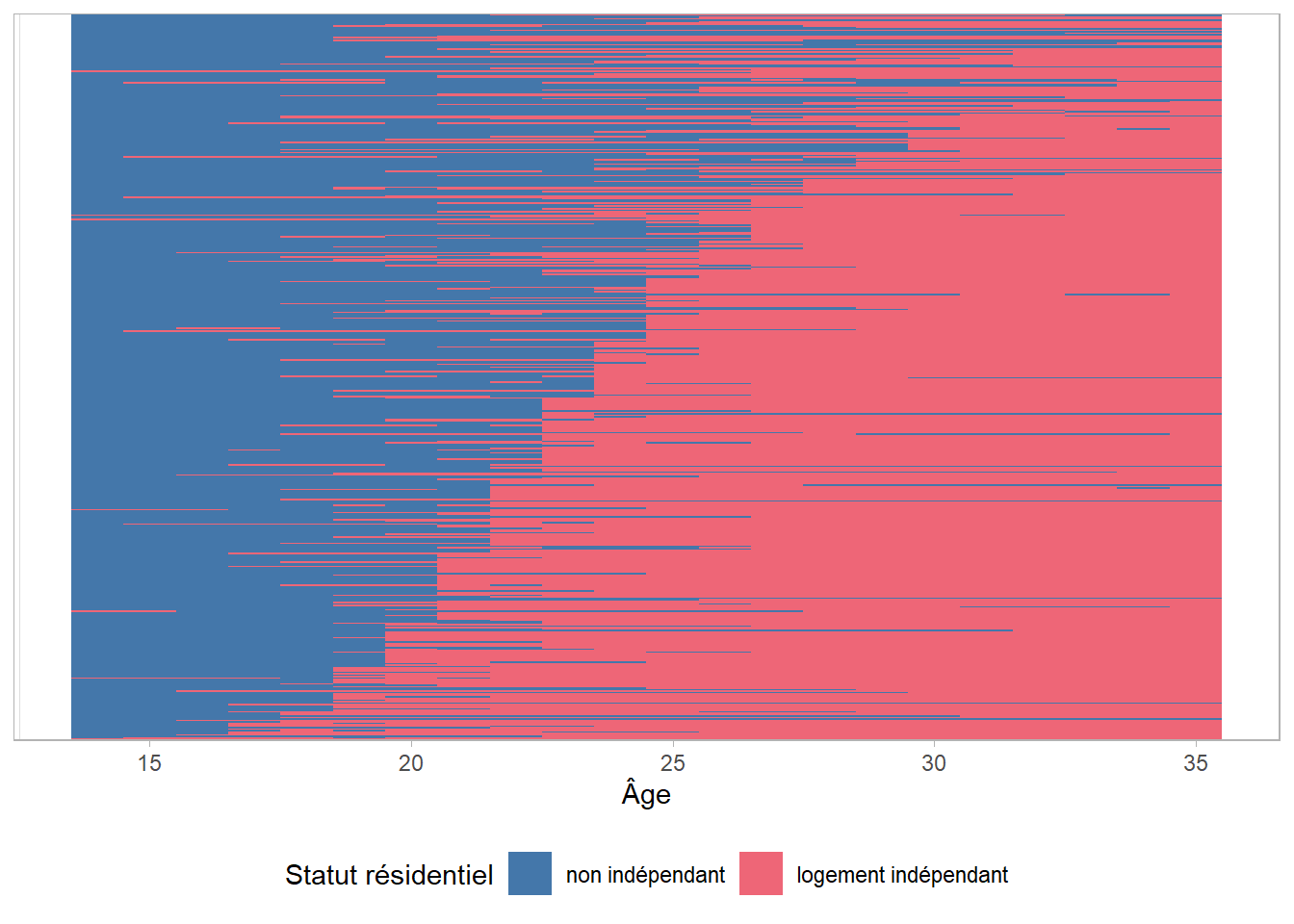
# ℹ 449 more rowsAjoutons cette variable au fichier long et trions notre graphique précédent selon cette variable.
Ici, les individus avec le plus petit âge à la première union sont représentés en bas du graphique. On voit une diagonale se dessiner et les individus les plus bas dans le graphique obtiennent également un logement indépendant plus tôt.
Il faut noter que certains individus n’ont pas vécu d’union avant 35 ans. Ces derniers n’apparaissent dans l’objet age_1u que nous avons créé plus tôt. Dès lors, après fusion, la variable age_1u a pour valeur NA pour ces derniers. Nous pourrions essayer d’isoler ces célibataires de longue durée
. Créons une variable dédiée.
Vérifions cette variable en dessinant les trajectoires matrimoniales par sous-groupe grâce à l’argument by.
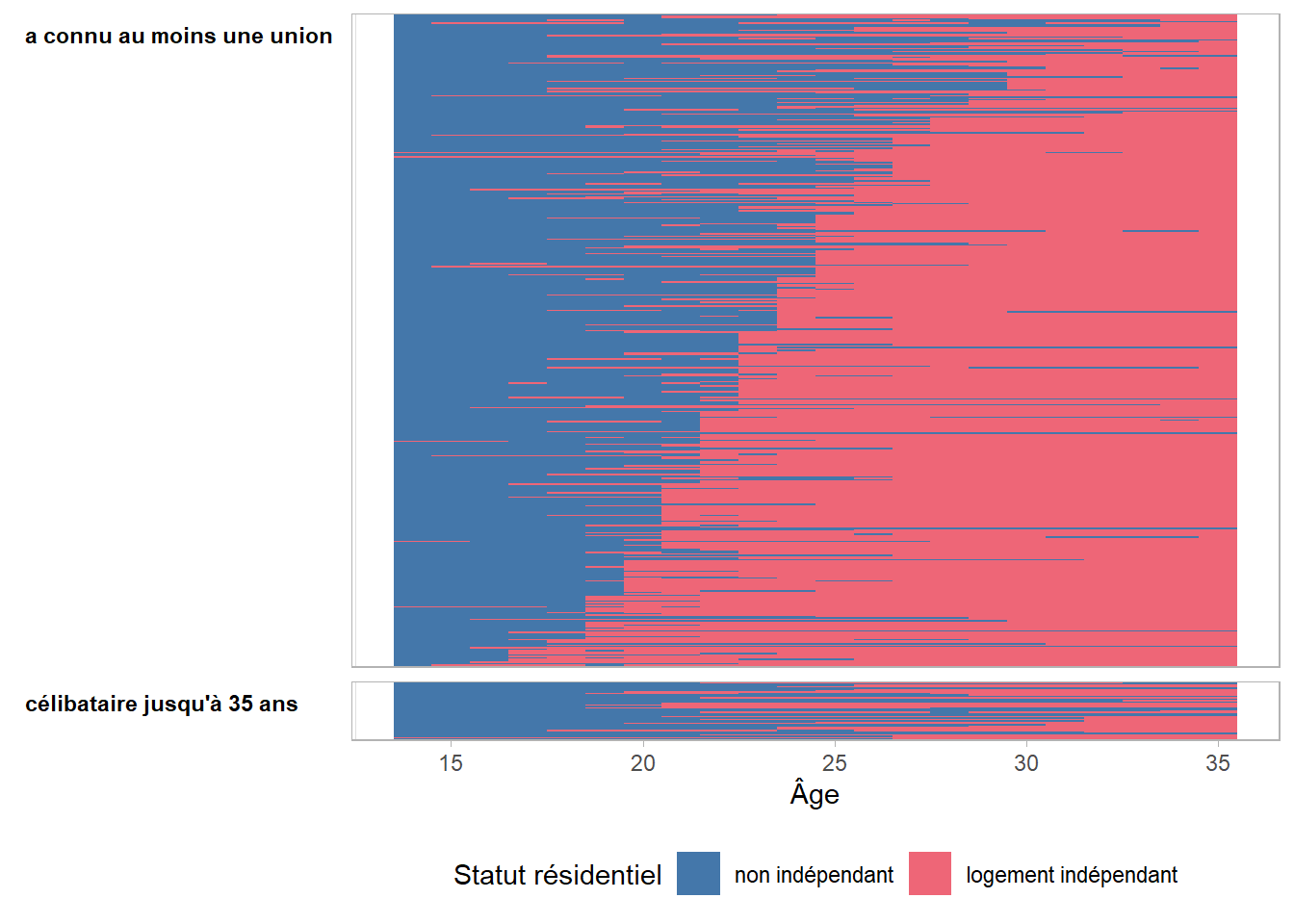
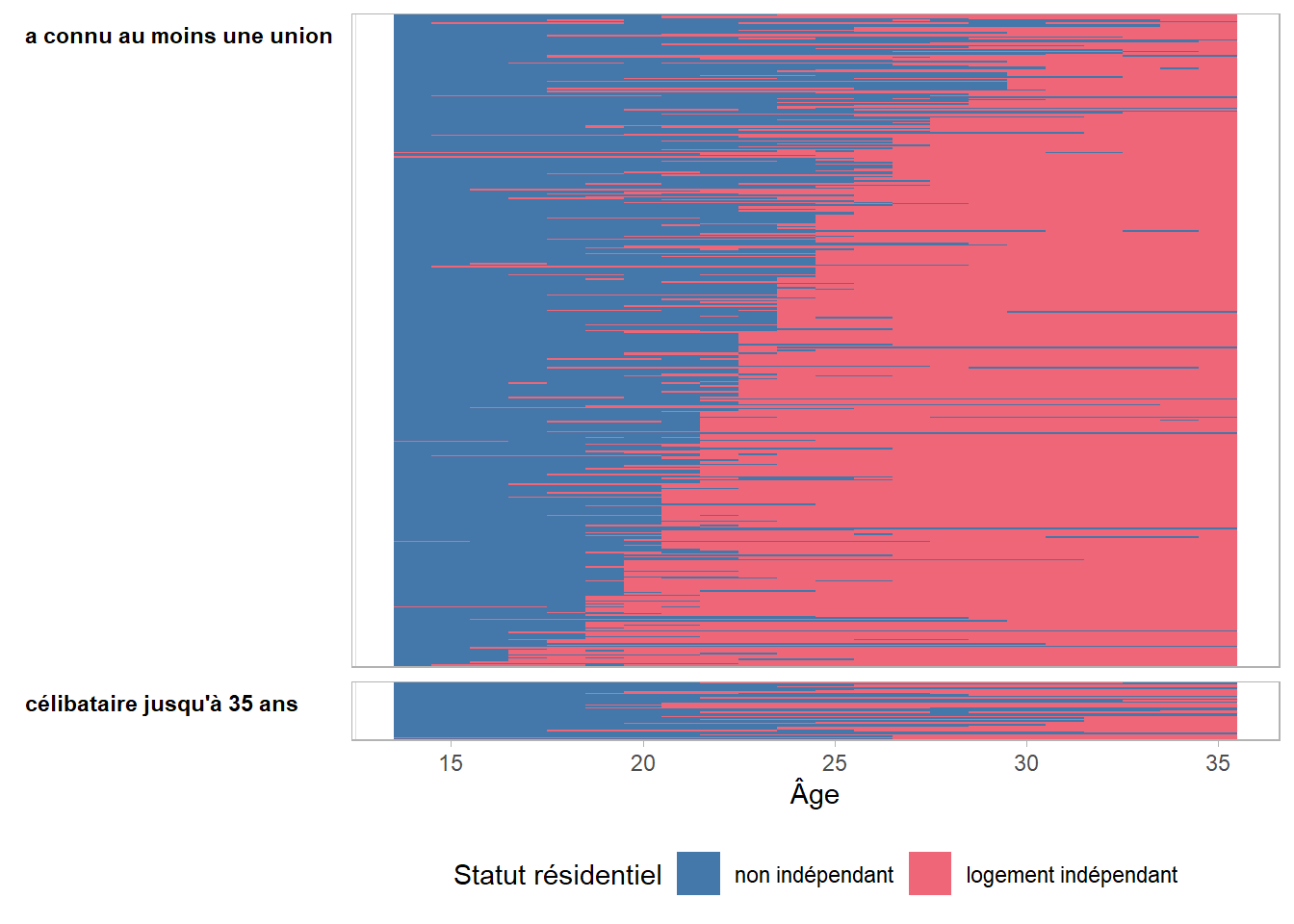
Refaisons notre graphique des trajectoirs résidentielle.
Nos célibataires
sont ici mieux isolés. En croisant les deux figures, il semble que pour celles et ceux qui se sont mis en union assez jeune, cela doit probablement correspondre au moment où ils ont eu un logement indépendant. Par contre, dans le haut du graphique, il y a plus d’hétérogénéité et l’accession à un logement indépenant semble moins corrélé à la mise en union.
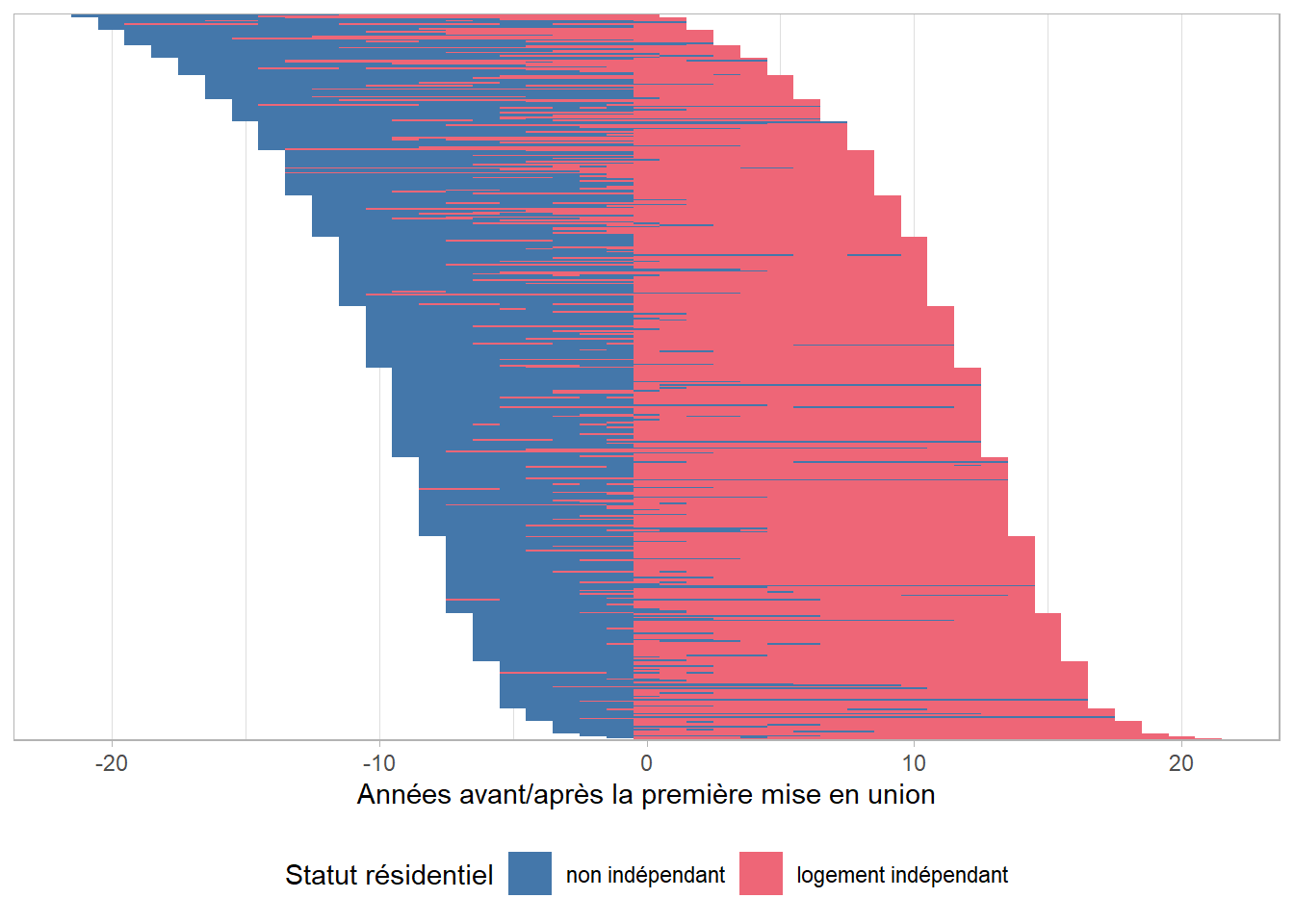
Pour poursuivre notre travail exploratoire, essayons de changer d’horloge et regardons comment évolue nos trajectoires si nous les centrons sur le moment de la mise en union. Calculons la durée (avant/après) par rapport à la première mise en union. Bien entendu, nos célibataires
seront exclus de l’analyse puisqu’ils n’ont pax d’âge de première mise en union.
Il n’y a plus qu’à redessiner nos trajectoires en changeant d’horloge.
dlong |>
filter(celib == "a connu au moins une union") |>
plot_trajectories(
id = id_ind,
time = duree_1u,
fill = slog,
sort_by = age_1u,
)
Il apparaît ici assez clairement que l’accès à un logement indépendant coïncide très souvent, dans notre échantillon, avec le moment de la première mise en union.
41.4 Pour aller plus loin
Nous l’avons vu, le format long est à privilégier en phase exploratoire car il facilite la création de nouvelles variables et les recodages. Il permet d’effectuer facilement et rapidement des premières analyses exploratoires.
Dans un second temps, et selon sa problématique et ses questions de recherche, on pourra se tourner vers des techniques d’analyses plus poussées, telles que l’analyse de survie (cf. Chapitre 44), l’analyse de séquences (cf. Chapitre 45), les modèles à classe latente ou encore les modèles à observations répétées. Selon les cas, il sera toujours possible de transformer ses données dans un format large ou périodique, selon les besoins.