45  Analyse de séquences

Dans ce chapitre, nous ferons une rapide introduction pratique à l’analyse de séquences, en mobilisant différents outils et fonctions déjà évoquées sur guide-R. Pour une présentation plus avancée et un cadrage théorique, on se référera à l’ouvrage de Nicolas Robette, L’analyse statistique des trajectoires, édité en 2021 par l’Ined dans la collection Méthodes et savoirs et disponible en ligne en accès freemium (<https://books.openedition.org/ined/16670>). D’autres ressources utiles sont indiquées en fin de chapitre.

De manière générale et simplifiée, l’analyse de séquences considère la trajectoire d’un individu comme une succession d’états¹ selon un pas de temps déterminé. Par exemple, le statut matrimonial d’un individu mesuré année après année pendant 15 ans pourrait être représenté comme la séquence C-C-C-RC-RC-M-M-M-M-M-D-D-D-M-M qui peut se lire ainsi : célibataire (C) pendant trois ans, puis en relation cohabitante (RC) pendant deux ans, marié (M) pendant cinq ans, divorcé (D) pendant trois ans et enfin remarié pendant deux ans.

¹ Il est également possible de considérer des séquences composées d’une succession d’évènements. Pour plus d’information, voir les références bibliographiques mentionnées en fin de chapitre.

Pour ce type d’analyse, il est donc essentiel de bien réfléchir en amont aux différents états possibles, au pas de temps considéré (ici l’année) et à l’horloge utilisée (par exemple l’âge, ou encore le temps depuis la fin des études).

L’objectif principal d’une l’analyse de séquences est d’identifier les séquences similaires afin de créer une typologie des différentes trajectoires. Pour cela, on calculera une distance entre les séquences, ce qui permettra de réaliser une classification automatisé (comme une classification ascendante hiérarchique, cf. Chapitre 43). La typologie obtenue pourra ensuite faire l’objet d’une analyse statistique plus classique (comme une régression logistique multinomiale, cf. Chapitre 46).

Le package de référence pour l’analyse de séquence est TraMineR.

45.1 Présentation des données de l’exemple

Nous allons utiliser le jeu de données seqhandbook::trajact fourni par le package seqhandbook et décrivant le statut professionnel entre 14 et 50 ans de 500 personnes interrogées dans le cadre de l’enquête Biographies et entourage réalisée par l’Ined en 2021.

library(seqhandbook)

Le chargement a nécessité le package : TraMineR

TraMineR stable version 2.2-12 (Built: 2025-07-03)

Website: http://traminer.unige.ch

Please type 'citation("TraMineR")' for citation information.

library(tidyverse)

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.6
✔ forcats   1.0.1     ✔ stringr   1.6.0
✔ ggplot2   4.0.1     ✔ tibble    3.3.0
✔ lubridate 1.9.4     ✔ tidyr     1.3.1
✔ purrr     1.2.0     

── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

trajact |> glimpse()

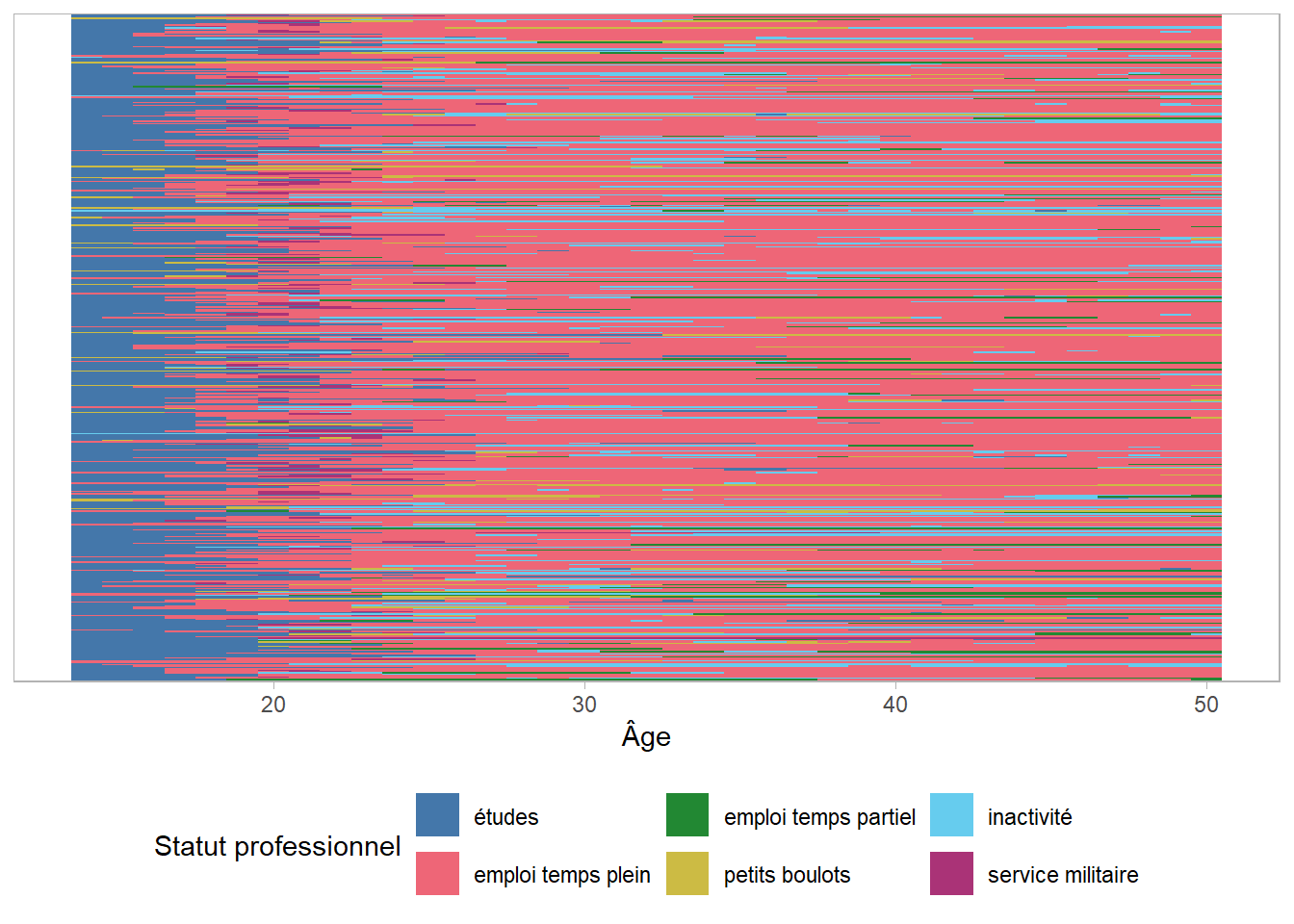
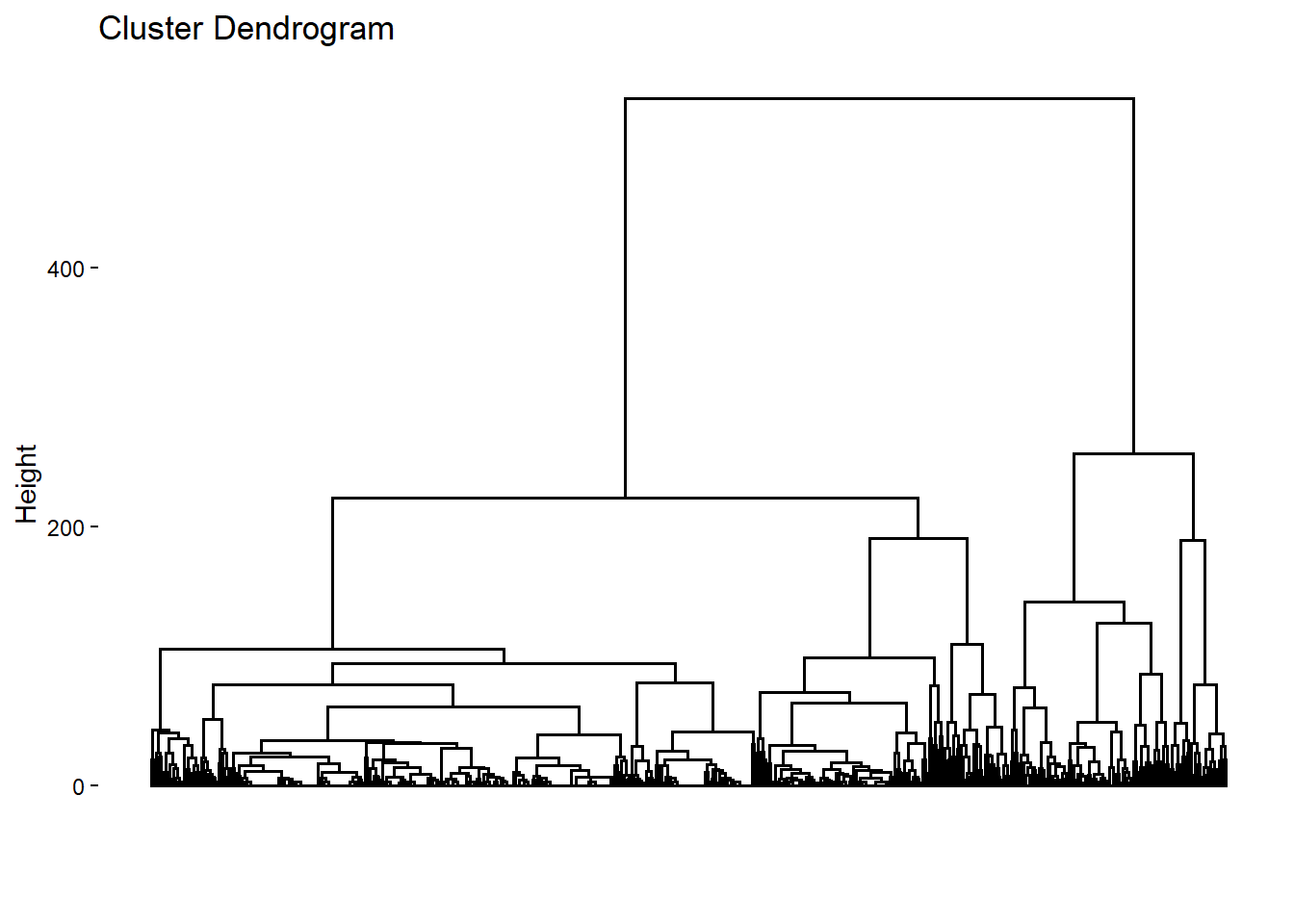
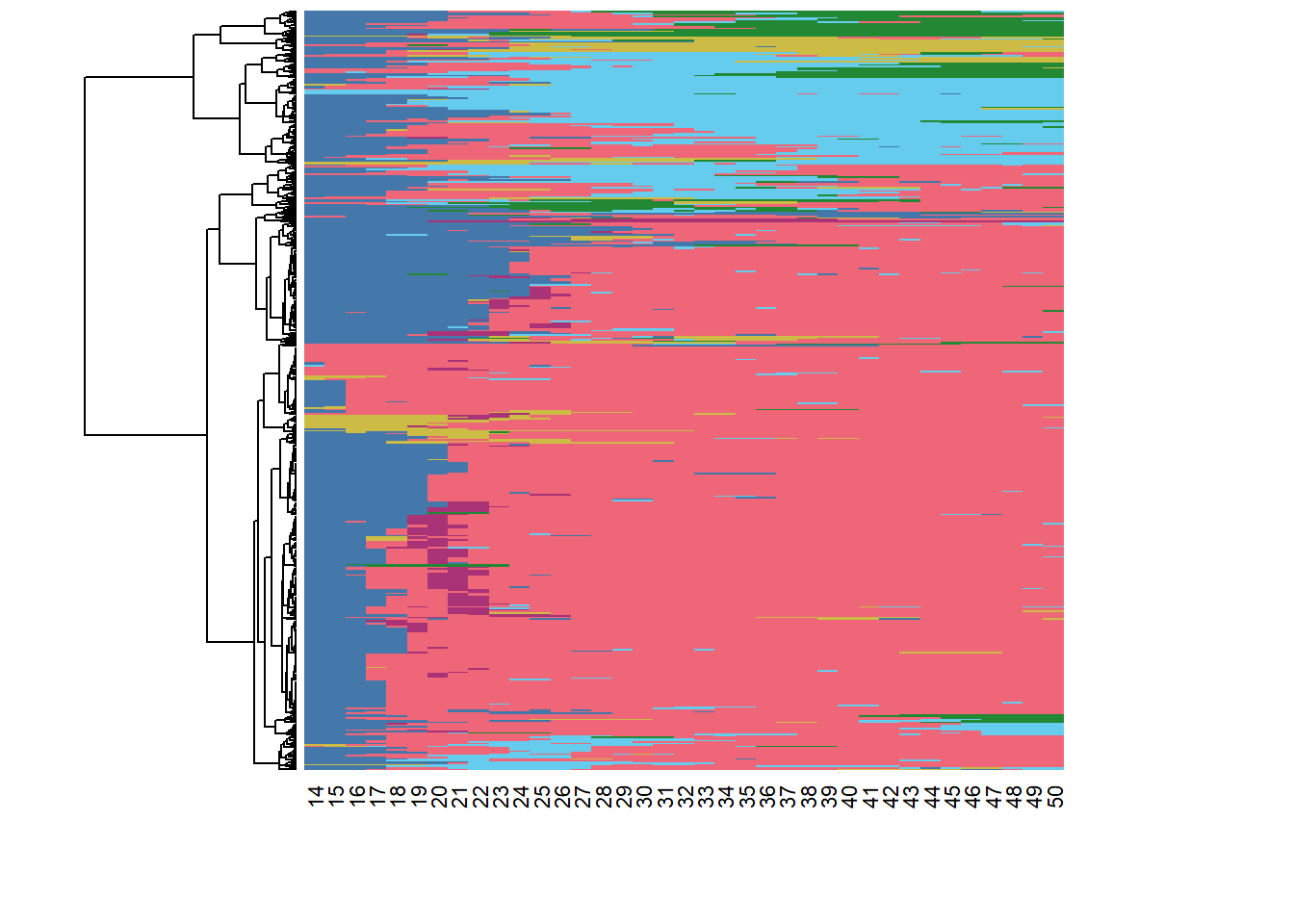
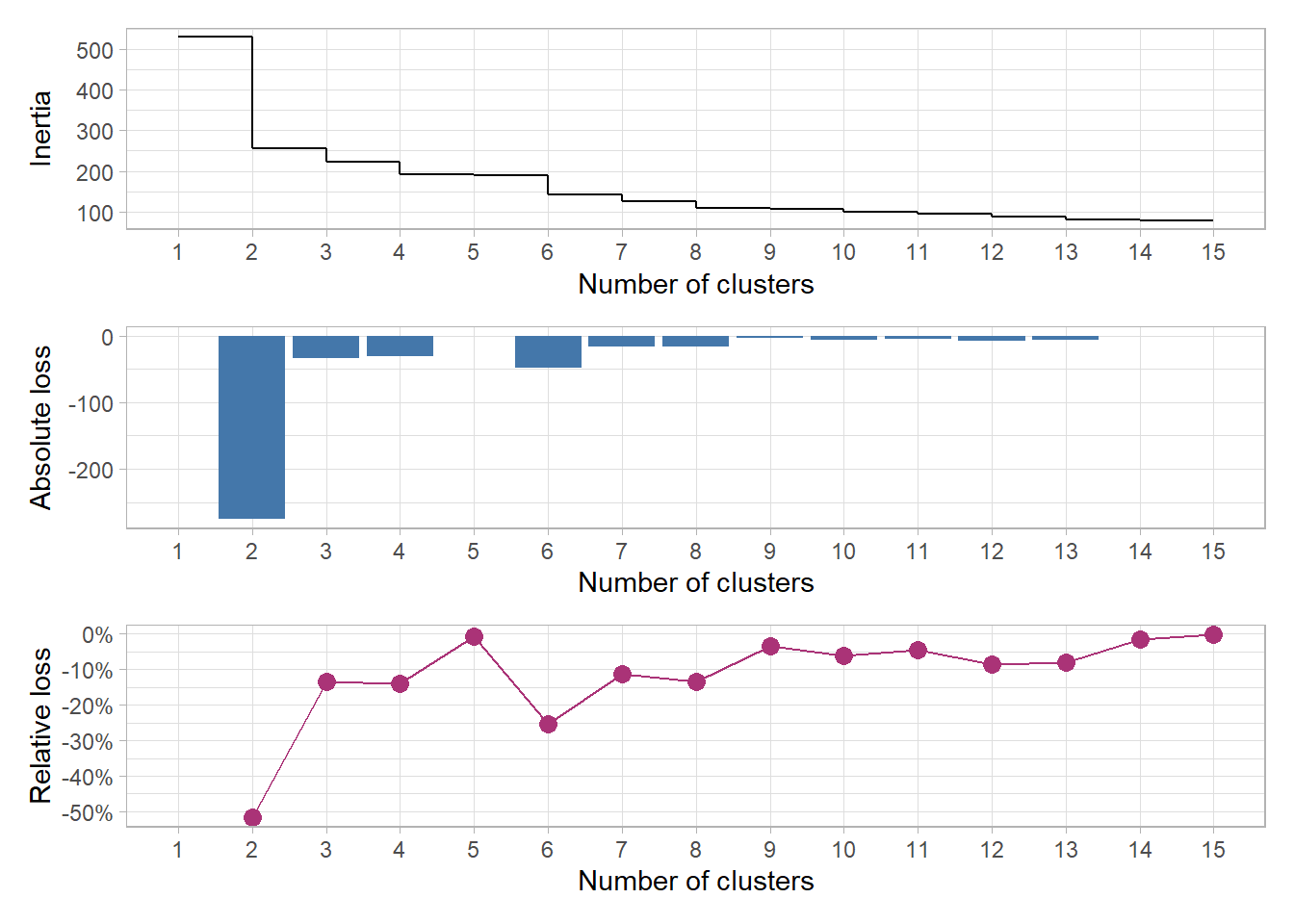
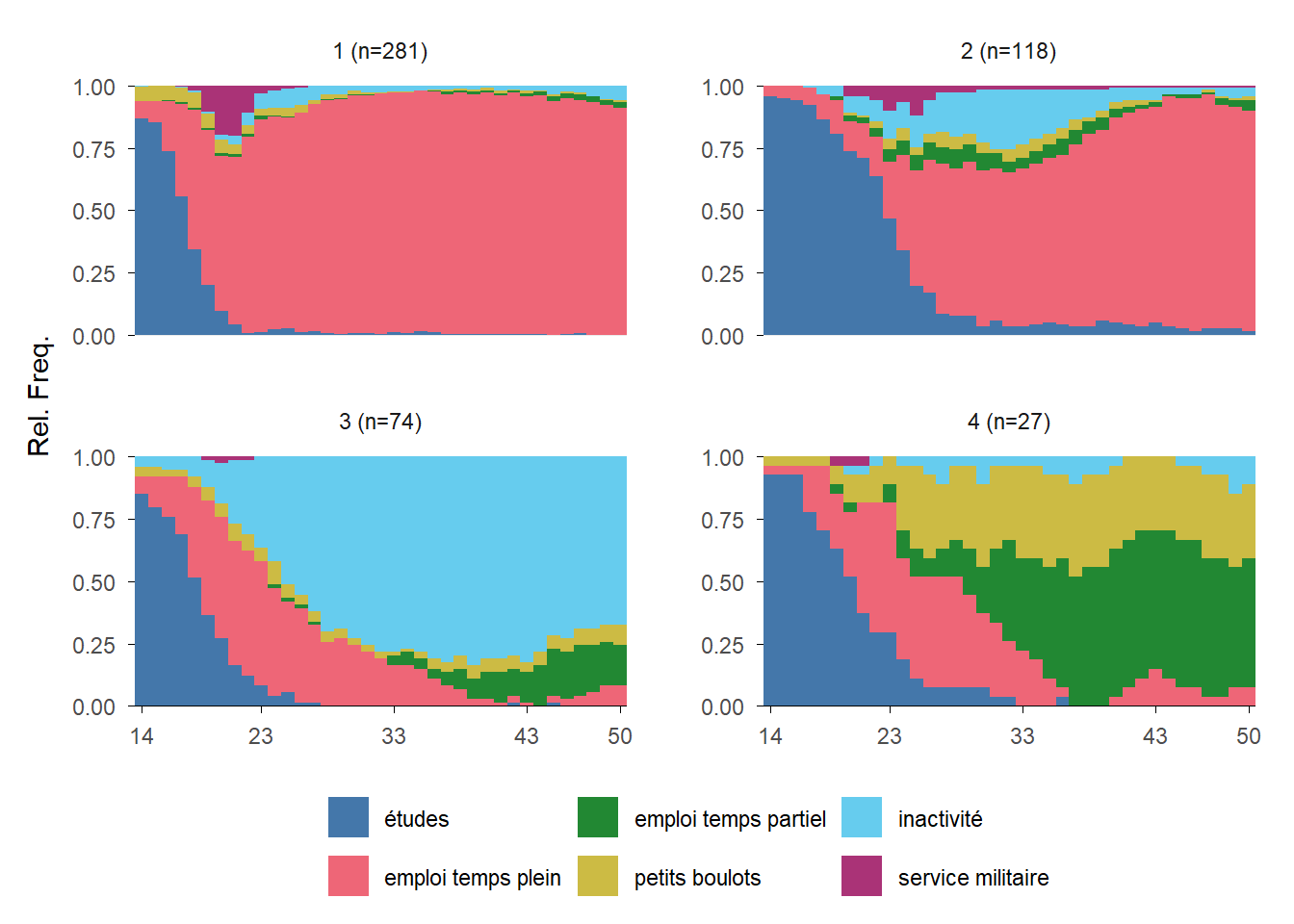
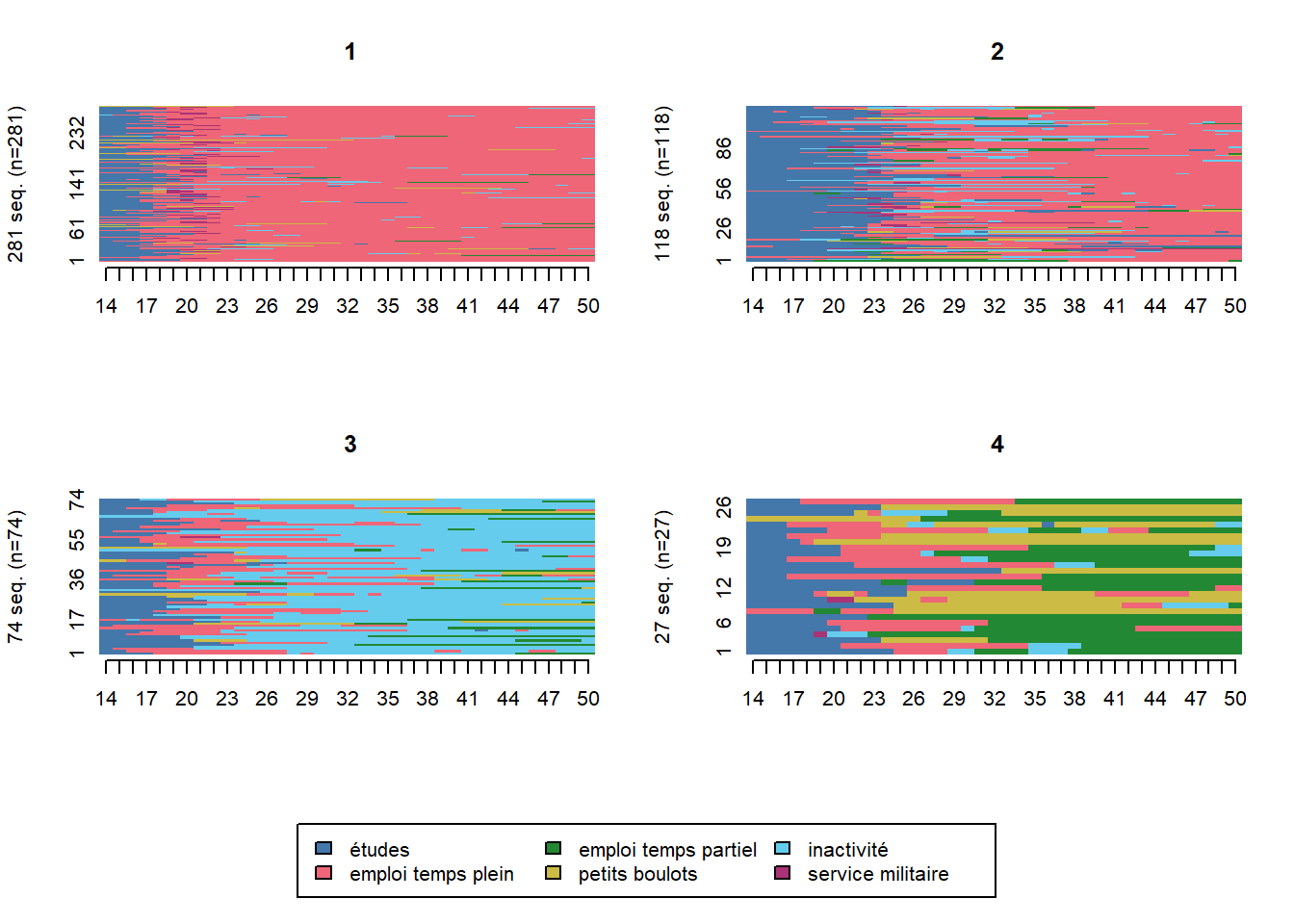
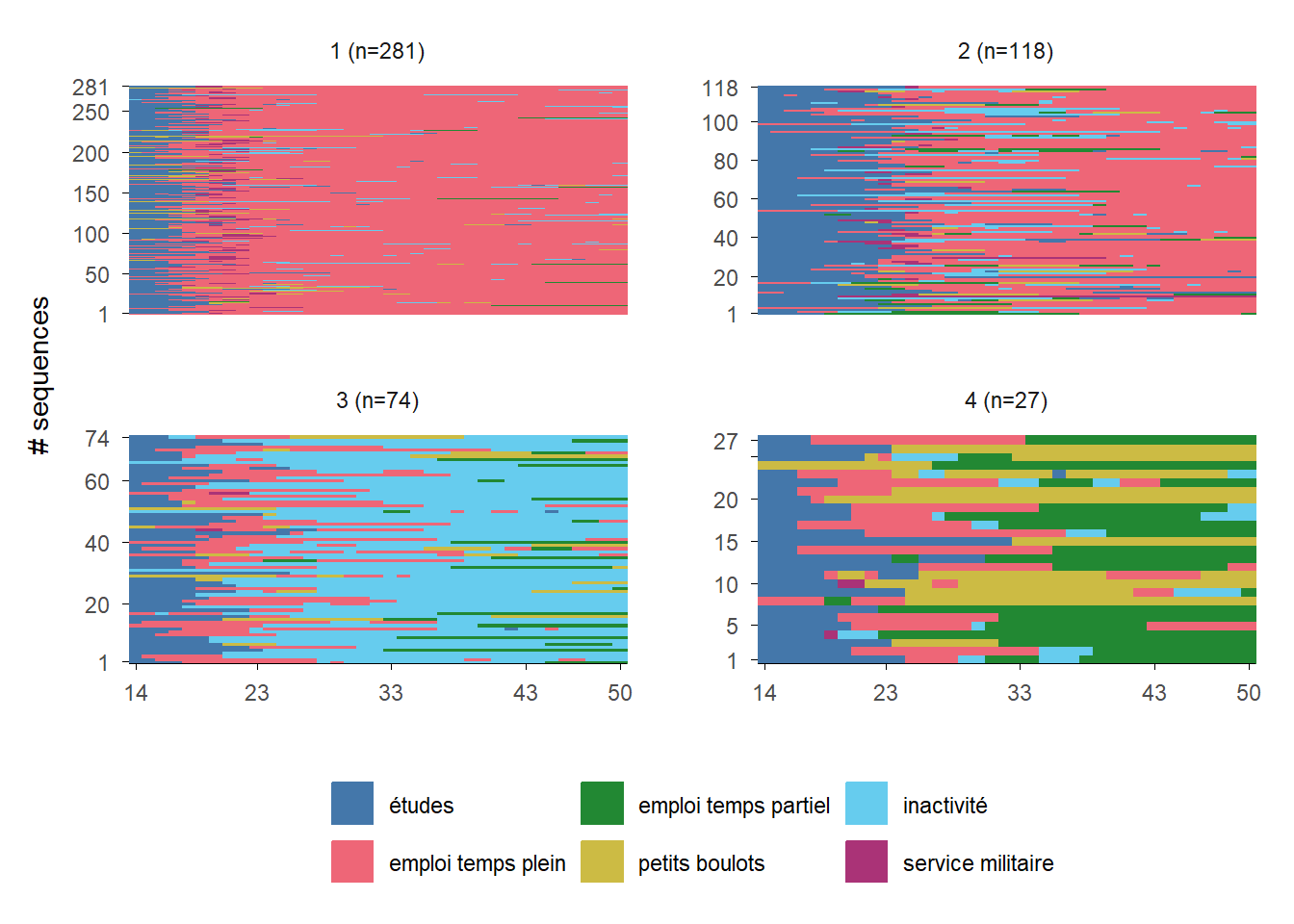
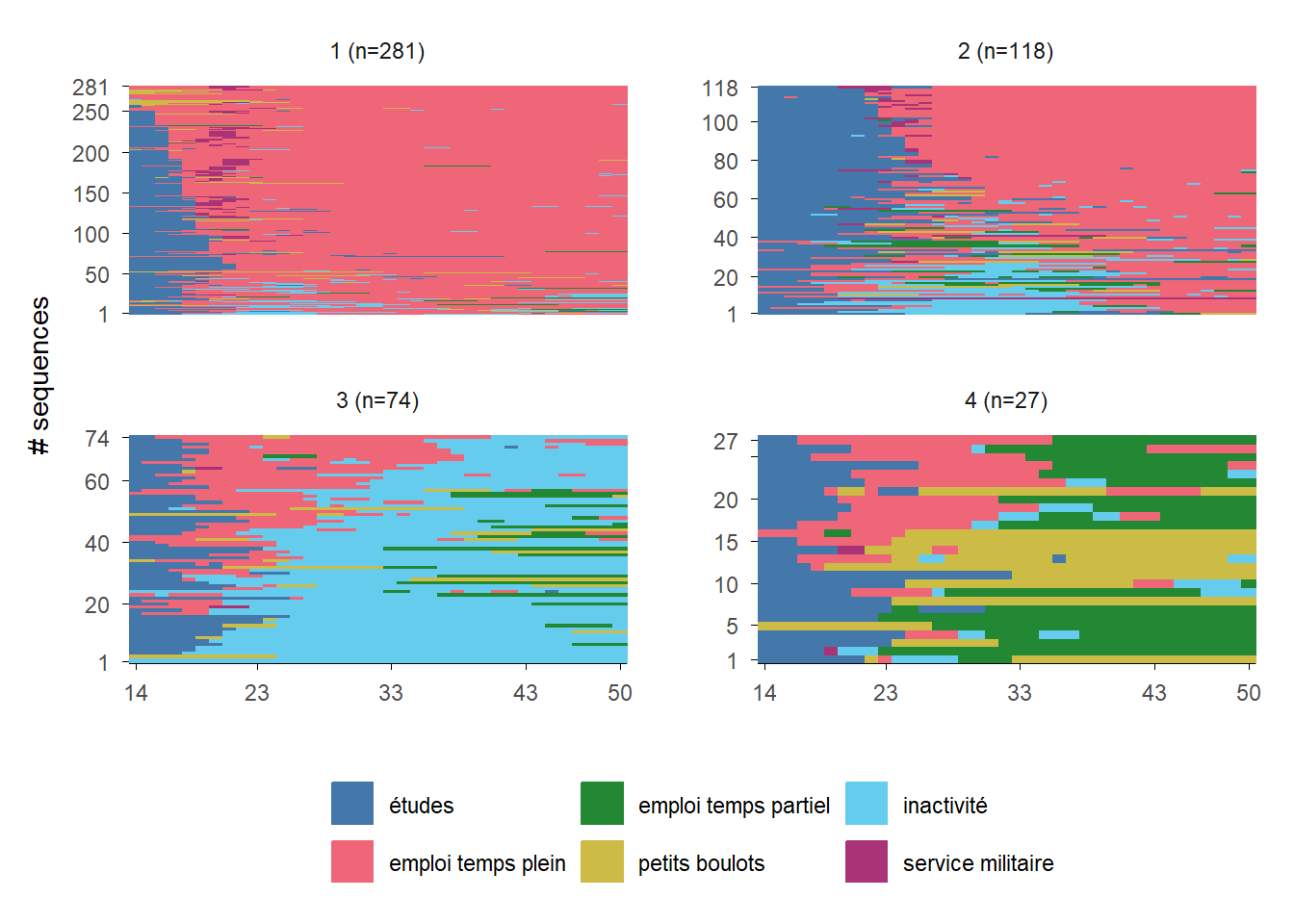
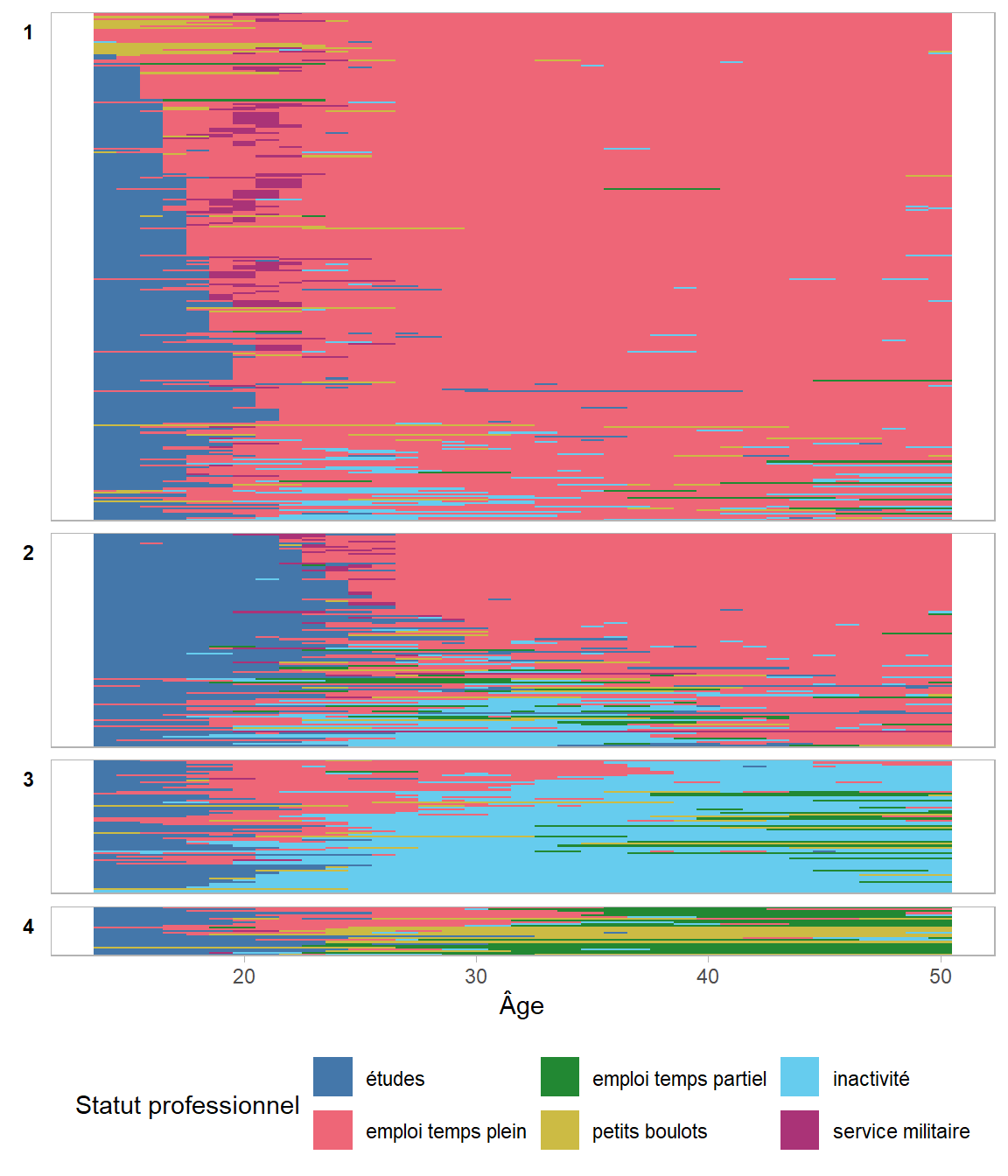
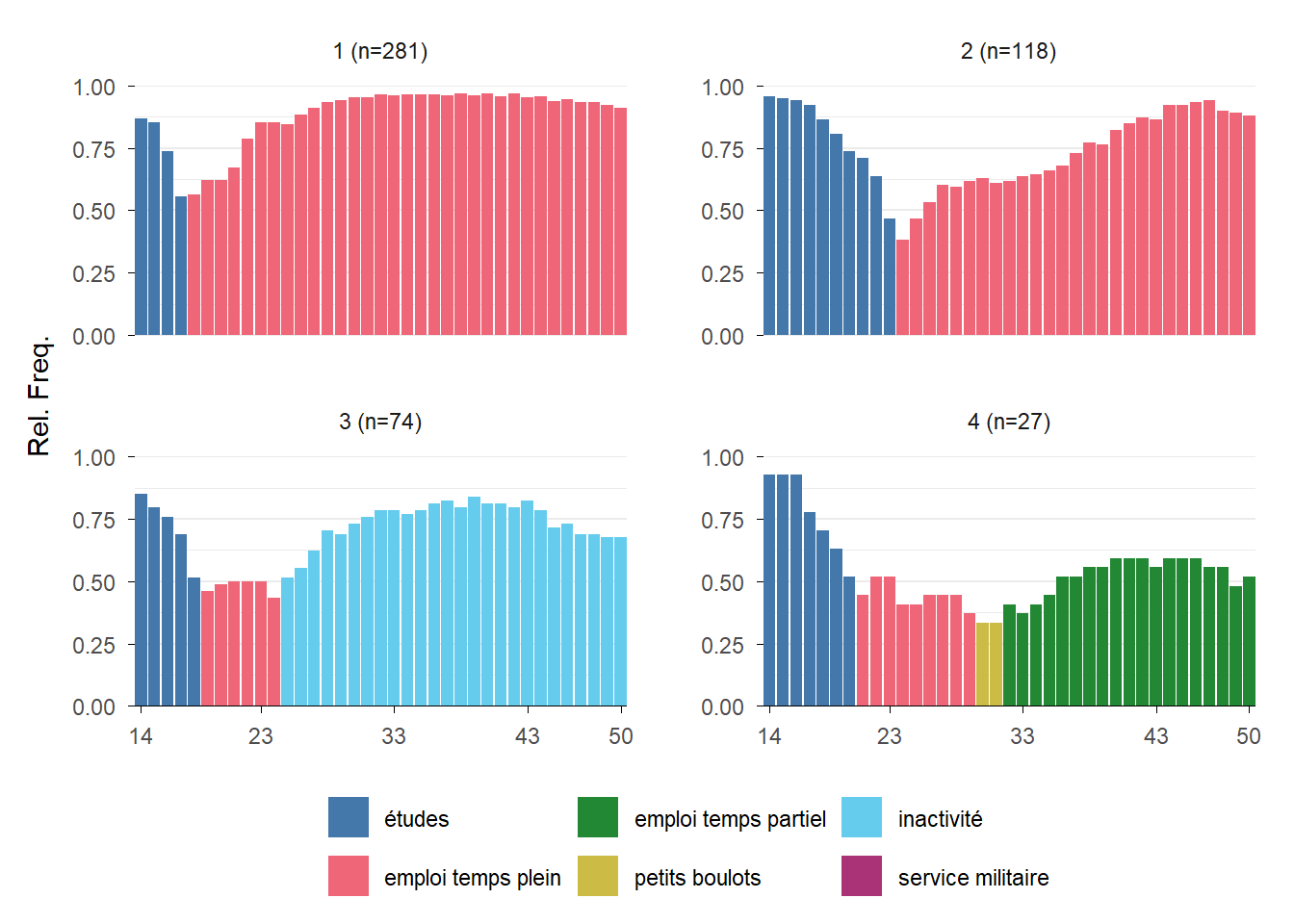
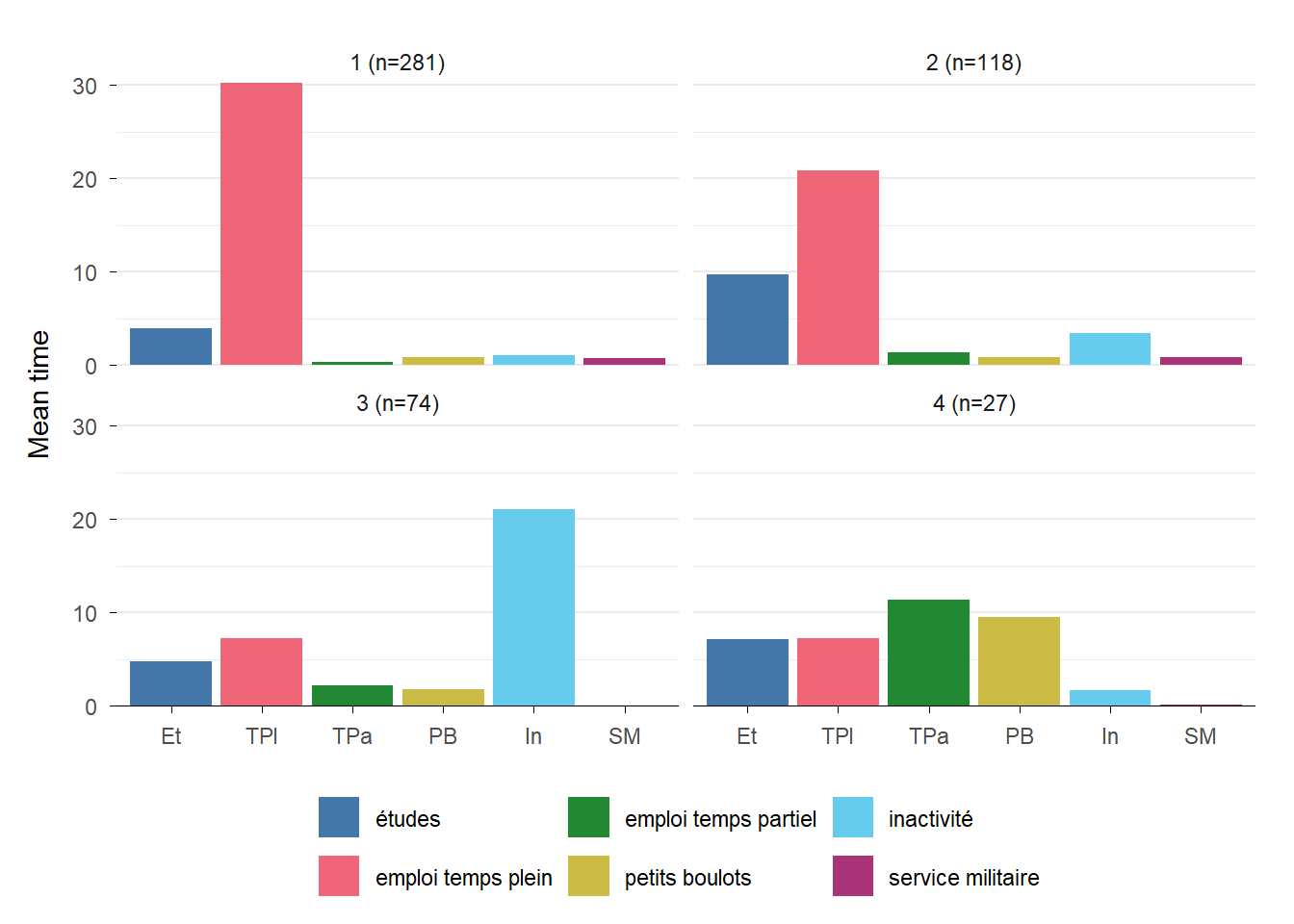
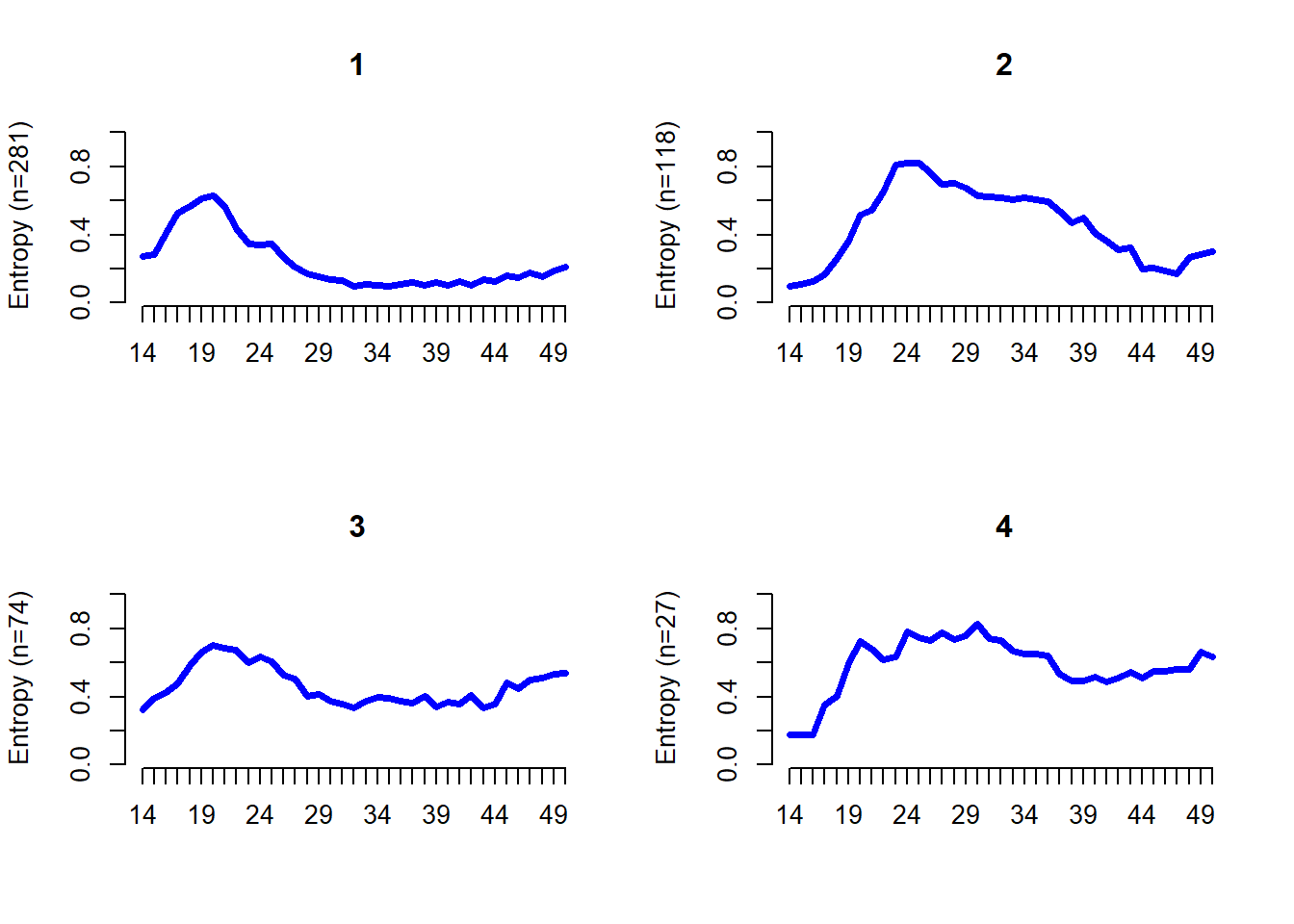
Rows: 500
Columns: 37
$ sact14 <dbl> 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, …
$ sact15 <dbl> 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 2, 1, 1, 1, 1, 1, …
$ sact16 <dbl> 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 2, 2, 1, 1, 1, 1, 1, …
$ sact17 <dbl> 2, 1, 1, 1, 1, 1, 2, 2, 2, 2, 1, 2, 2, 1, 2, 2, 1, 2, 1, 1, 1, …
$ sact18 <dbl> 2, 1, 2, 2, 1, 1, 2, 2, 2, 2, 1, 2, 2, 1, 2, 2, 1, 2, 1, 1, 1, …
$ sact19 <dbl> 2, 3, 2, 2, 1, 1, 2, 2, 2, 2, 1, 2, 2, 1, 2, 2, 2, 2, 1, 1, 1, …
$ sact20 <dbl> 2, 3, 2, 6, 2, 2, 5, 2, 6, 2, 1, 2, 2, 1, 2, 2, 2, 2, 1, 1, 1, …
$ sact21 <dbl> 2, 3, 2, 2, 2, 2, 5, 6, 6, 2, 1, 2, 5, 5, 2, 2, 2, 2, 1, 1, 1, …
$ sact22 <dbl> 2, 3, 2, 2, 2, 2, 5, 6, 2, 2, 1, 2, 5, 5, 2, 2, 2, 2, 1, 1, 1, …
$ sact23 <dbl> 2, 3, 2, 2, 2, 2, 5, 2, 2, 2, 1, 2, 5, 5, 2, 4, 6, 2, 1, 1, 2, …
$ sact24 <dbl> 2, 3, 2, 2, 2, 5, 3, 2, 2, 2, 1, 2, 5, 5, 2, 4, 6, 2, 5, 1, 2, …
$ sact25 <dbl> 2, 3, 2, 2, 2, 5, 3, 2, 2, 2, 2, 2, 5, 5, 2, 4, 6, 2, 5, 1, 2, …
$ sact26 <dbl> 2, 3, 2, 2, 2, 5, 3, 2, 2, 2, 2, 2, 5, 5, 2, 4, 6, 2, 5, 1, 2, …
$ sact27 <dbl> 2, 3, 2, 2, 2, 2, 3, 2, 2, 2, 2, 2, 5, 5, 2, 4, 2, 2, 5, 2, 2, …
$ sact28 <dbl> 2, 3, 5, 2, 2, 2, 3, 2, 2, 2, 2, 5, 5, 5, 2, 4, 2, 2, 5, 2, 2, …
$ sact29 <dbl> 2, 3, 2, 2, 2, 2, 3, 2, 2, 2, 2, 5, 5, 5, 2, 4, 2, 2, 5, 2, 2, …
$ sact30 <dbl> 2, 3, 5, 2, 2, 2, 3, 2, 2, 2, 2, 5, 5, 5, 2, 4, 2, 2, 5, 2, 2, …
$ sact31 <dbl> 2, 3, 5, 2, 2, 2, 3, 2, 2, 2, 2, 5, 5, 5, 2, 4, 2, 2, 5, 2, 5, …
$ sact32 <dbl> 2, 3, 5, 2, 2, 2, 5, 2, 2, 2, 2, 5, 5, 5, 2, 4, 2, 2, 5, 2, 5, …
$ sact33 <dbl> 2, 3, 5, 2, 2, 2, 5, 2, 2, 2, 2, 5, 5, 5, 2, 5, 2, 2, 3, 2, 5, …
$ sact34 <dbl> 2, 3, 5, 2, 2, 2, 5, 2, 2, 2, 2, 5, 5, 5, 2, 5, 2, 2, 3, 2, 5, …
$ sact35 <dbl> 2, 3, 5, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 2, 5, 2, 2, 3, 2, 5, …
$ sact36 <dbl> 2, 3, 5, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 2, 5, 2, 2, 3, 2, 5, …
$ sact37 <dbl> 2, 3, 5, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 2, 5, 2, 2, 3, 2, 5, …
$ sact38 <dbl> 2, 2, 5, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 2, 5, 2, 2, 3, 2, 5, …
$ sact39 <dbl> 2, 2, 5, 2, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 2, 5, 2, 2, 3, 2, 5, …
$ sact40 <dbl> 2, 2, 5, 2, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 2, 5, 2, 2, 3, 2, 5, …
$ sact41 <dbl> 2, 2, 5, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 2, 5, 2, 2, 3, 2, 5, …
$ sact42 <dbl> 2, 2, 5, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 2, 5, 2, 2, 3, 2, 5, …
$ sact43 <dbl> 2, 2, 5, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 2, 2, 2, 2, 3, 2, 5, …
$ sact44 <dbl> 2, 2, 5, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 2, 2, 2, 2, 3, 2, 5, …
$ sact45 <dbl> 2, 2, 3, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 2, 2, 2, 2, 3, 2, 5, …
$ sact46 <dbl> 2, 2, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 2, 2, 2, 2, 3, 2, 5, …
$ sact47 <dbl> 2, 2, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 2, 2, 2, 2, 3, 2, 5, …
$ sact48 <dbl> 2, 2, 3, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 2, 2, 2, 2, 3, 2, 5, …
$ sact49 <dbl> 2, 2, 3, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 2, 2, 2, 2, 3, 2, 5, …
$ sact50 <dbl> 2, 3, 3, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 2, 2, 2, 2, 3, 2, 5, …

Comme nous pouvons le voir, les données sont ici organisées selon un format large : nous avons 500 lignes, correspondant aux 500 personnes enquêtées, et 37 variables, chacune indiquant le statut professionnel à un âge donné.

Le format large est celui le plus souvent utilisé pour l’analyse de séquences et celui que vous retrouverez dans les différents exemples et tutoriels des références listées en fin de chapitre. Cependant, comme nous l’avons évoqué dans le chapitre sur les données longitudinales (cf. Chapitre 41), ce format n’est pas pratique si l’on a encore du travail préliminaire (comme des recodages) à effectuer. Ici, nous allons transformer les données dans un format long et nous présenterons plus loin comment créer un objet séquences à partir d’un format long. Nous allons aussi en profiter pour créer un identifiant individu et documenter les variables. Pour cet identifiant, nous allons le préfixer avec "IND_" pour facilement vérifier qu’il est bien conservé tout au long du processus et allons utiliser guideR::leading_zeros() pour que tous les identifiants aient le même nombre de chiffres (i.e. IND_001 au lieu de IND_1).

library(labelled)

trajact <-
  trajact |> 
  mutate(
    id_ind = paste0(
      "IND_",
      guideR::leading_zeros(row_number())
    )
  )

d <-
  trajact |> 
  pivot_longer(
    cols = starts_with("sact"),
    names_to = "age",
    names_prefix = "sact",
    values_to = "statut_pro"
  ) |> 
  mutate(age = as.integer(age)) |> 
  set_variable_labels(
    id_ind = "Identifiant individu",
    age = "Âge",
    statut_pro = "Statut professionnel"
  ) |> 
  set_value_labels(
    statut_pro = c(
      "études" = 1,
      "emploi temps plein" = 2,
      "emploi temps partiel" = 3,
      "petits boulots" = 4,
      "inactivité" = 5,
      "service militaire" = 6
    )
  )

Notez ici que le statut professionnel est codé de manière numérique. Nous avons donc ajouté des étiquettes de valeurs (cf. Chapitre 12). Notre variable statut_pro est donc pour le moment au format numérique labellisé.

d |> look_for(details = TRUE) |> to_gt()

#	Variable	Type	Variable label	Values	Missing values	Unique values
1	id_ind	chr	Identifiant individu	IND_001 – IND_500	0	500
2	age	int	Âge	14 – 50	0	37
3	statut_pro	dbl+lbl	Statut professionnel	[1] études[2] emploi temps plein[3] emploi temps partiel[4] petits boulots[5] inactivité[6] service militaire [1] études [2] emploi temps plein [3] emploi temps partiel [4] petits boulots [5] inactivité [6] service militaire	0	6

Pour jeter un œil rapide aux trajectoires individuelles, on pourra utiliser la fonction guideR::plot_trajectories() fournie par guideR, le package compagnon de guide-R. À noter, pour cette fonction (comme à chaque fois que l’on fait un graphique ou un tableau), le statut professionnel doit être codé sous forme de facteur. Nous allons donc faire la conversion à la volée avec labelled::unlabelled().

library(guideR)
d |> 
  unlabelled() |> 
  plot_trajectories(
    id = id_ind,
    time = age,
    fill = statut_pro
  )

45.2 Création d’un objet séquences

Pour la suite des analyses avec TraMineR, nous allons devoir créer un objet STS (STate Sequence) qui correspond à une séquence d’états. Cela se fait à l’aide de la fonction TraMineR::seqdef(). Cependant, il y a un tout petit peu de travail en amont.

En premier lieu, nous devons définir un alphabet qui correspond aux différents états considérés. Il peut s’agir de nombres ou bien de lettres. Nous pouvons garder par exemple les codes 1 à 6 actuellement utilisés dans nos données.

C’est optionnel, mais il peut être utile de définir des noms courts de quelques lettres qui serviront de moyen mnémotechnique et qui seront utilisés par TraMineR en différents endroits. C’est toujours utile. Alternativement, nous pouvons modifier nos données d’un vecteur numérique labellisé en un vecteur textuel labellisé.

Toujours optionnel, nous pouvons définir des étiquettes ou noms longs qui seront utilisées dans différentes sorties graphiques. Ici, nous allons prendre les étiquettes que nous avons défini précédemment avec labelled::set_value_labels(). Pour cela, nous utiliser la fonction labelled::get_value_labels(). Cependant, il faut se rappeler que le retour de cette fonction est un vecteur des valeurs nommé avec les étiquettes. On appliquera donc la fonction names() pour récupérer les étiquettes.

L’argument cname permet de donner une étiquette courte pour les pas de temps, étiquettes réutilisées dans les sorties graphiques. Ici, nous utiliserons directement 14:50 pour simplement afficher l’âge des individus.

Enfin, toujours optionnel, on peut également passer un vecteur de couleurs qui seront utilisées par les différentes sorties graphiques. Ici, nous allons utiliser la palette de couleurs guideR::safe_pal() (voir le chapitre sur les couleurs, cf. Chapitre 16).

noms_courts <- c("Et", "TPl", "TPa", "PB", "In", "SM")
etiquettes <- d$statut_pro |> get_value_labels() |> names()
palette <- guideR::safe_pal()(6)

# alternative aux noms courts
d <- d |> 
  mutate(
    statut_pro2 = case_when(
      statut_pro == 1 ~ "Et",
      statut_pro == 2 ~ "TPl",
      statut_pro == 3 ~ "TPa",
      statut_pro == 4 ~ "PB",
      statut_pro == 5 ~ "In",
      statut_pro == 6 ~ "SM"
    )
  ) |> 
  set_value_labels(
    statut_pro2 = c(
      "études" = "Et",
      "emploi temps plein" = "TPl",
      "emploi temps partiel" = "TPa",
      "petits boulots" = "PB",
      "inactivité" = "In",
      "service militaire" = "SM"
    )
  ) |> 
  set_variable_labels(
    statut_pro2 = "Statut professionnel"
  )
d |> look_for("statut_pro2") |> to_gt()

#	Variable	Type	Variable label	Values	Missing values
4	statut_pro2	chr+lbl	Statut professionnel	[Et] études[TPl] emploi temps plein[TPa] emploi temps partiel[PB] petits boulots[In] inactivité[SM] service militaire [Et] études [TPl] emploi temps plein [TPa] emploi temps partiel [PB] petits boulots [In] inactivité [SM] service militaire	0

Dans de nombreux tutoriels, dont celui de Nicolas Robette associé à son ouvrage, la création d’un objet séquence est réalisée à partir d’un format large, qui est le format attendu par défaut par TraMineR::seqdef(). Dans cette situation, on passera à la fonction uniquement les colonnes concernées avec les options à considérer. On peut éventuellement définir l’identifiant des individus avec le paramètre id. Cela est fortement conseillé car cela permettra, en bout de chaîne, de correctement réidentifier les individus.

seq <-
  seqdef(
    data = trajact |> select(-id_ind),
    id = trajact$id_ind,
    labels = etiquettes,
    states = noms_courts,
    cpal = palette,
    cname = 14:50
  )

 [>] state coding:

       [alphabet]  [label]  [long label] 

     1  1           Et       études

     2  2           TPl      emploi temps plein

     3  3           TPa      emploi temps partiel

     4  4           PB       petits boulots

     5  5           In       inactivité

     6  6           SM       service militaire

 [>] 500 sequences in the data set

 [>] min/max sequence length: 37/37

Si, comme nous, nous avons nos données dans un format long, nous pouvons aisément les transformer au format STS attendu par TraMineR::seqdef() grâce à la fonction TraMineR::seqformat(). En effet, notre format long est une variante du format SPELL qui est le nom utilisé par TraMineR d’un format périodique ou chaque ligne est définie par une variable indiquant le début de la période et une variable indiquant la fin de la période. Il nous suffit en effet d’indiquer la variable age comme correspondant à la fois au début et à la fin de chaque période. Ici, nous allons utiliser notre nouvelle variable statut_pro2, ce qui nous permet de ne plus avoir besoin de noms courts.

seq <-
  d |> 
  seqformat(
    from = "SPELL",
    to = "STS",
    id = "id_ind",
    begin = "age",
    end = "age",
    status = "statut_pro2",
    process = FALSE
  ) |> 
  seqdef(
    labels = etiquettes,
    cpal = palette,
    cname = 14:50
  )

 [>] time axis: 14 -> 50

 [>] converting SPELL data into 500 STS sequences (internal format)

 [>] 6 distinct states appear in the data: 

     1 = Et

     2 = In

     3 = PB

     4 = SM

     5 = TPa

     6 = TPl

 [>] state coding:

       [alphabet]  [label]  [long label] 

     1  Et          Et       études

     2  In          In       emploi temps plein

     3  PB          PB       emploi temps partiel

     4  SM          SM       petits boulots

     5  TPa         TPa      inactivité

     6  TPl         TPl      service militaire

 [>] 500 sequences in the data set

 [>] min/max sequence length: 37/37

Astuce

Cette étape peut être facilitée grâce à la fonction guideR::long_to_seq() qui réalise directement la transformation précédente. De plus, si le statut est stocké sous forme de vecteur labellisé, la fonction extrait automatiquement les étiquettes. Enfin, elle utilise guideR::safe_pal() comme palette de couleur par défaut.

library(guideR)
seq <-
  d |> 
  long_to_seq(
    id = id_ind,
    time = age,
    outcome = statut_pro2
  )

 [>] time axis: 14 -> 50

 [>] converting SPELL data into 500 STS sequences (internal format)

 [>] 6 distinct states appear in the data: 

     1 = Et

     2 = In

     3 = PB

     4 = SM

     5 = TPa

     6 = TPl

 [>] state coding:

       [alphabet]  [label]  [long label] 

     1  Et          Et       études

     2  TPl         TPl      emploi temps plein

     3  TPa         TPa      emploi temps partiel

     4  PB          PB       petits boulots

     5  In          In       inactivité

     6  SM          SM       service militaire

 [>] 500 sequences in the data set

 [>] min/max sequence length: 37/37

Note

Si l’on travaille avec des données pondérées, il est possible de passer à TraMineR::seqdef() (ou guideR::long_to_seq()) un vecteur de poids individuels avec l’argument weights. Afin d’éviter toute erreur si vous travaillez avec des données au format long, il est conseillé de trier en amont son fichier long selon l’identifiant individu. Le vecteur de poids sera lui aussi trié selon l’identifiant, afin d’éviter toute mauvaise association au moment de la création du fichier de séquences.

45.3 Construction d’une typologie

45.3.1 Calcul d’une matrice des distances

Comme dans le cadre d’une classification ascendante hiérarchique (cf. Chapitre 43), la première étape consiste à calculer une matrice des distances entre les différentes séquences.

Il existe de nombreux types de distances différents, chacun ayant ses avantages et ses inconvénients. La lecture du chapitre Mesurer la dissemblance entre trajectoires de l’ouvrage de Nicolas Robette est ici fortement conseillée. On pourra également se référer à cet article (en anglais) de Matthias Studer et Gilbert Ritschard.

L’approche usuelle en analyse de séquences est l’appariement optimal ou optimal matching. Cette méthode consiste, pour chaque paire de séquences, à compter le nombre minimal de modifications (substitutions, suppressions, insertions) qu’il faut faire subir à l’une des séquences pour obtenir l’autre. On peut considérer que chaque modification est équivalente, mais il est aussi possible de prendre en compte le fait que les distances entre les différents états n’ont pas toutes la même valeur (par exemple, la distance sociale entre emploi à temps plein et chômage est plus grande qu’entre emploi à temps plein et emploi à temps partiel), en assignant aux différentes modifications des coûts distincts. C’est notamment pertinent si l’on peut ordonner les différents statuts.

Dans le cas général, on considérera que les coûts de substitution sont identiques entre tous les statuts et, en pratique, on les fixera à 2. Reste à déterminer les coûts d’insertion/suppression (indel) d’un statut en début ou en fin de ligne. Selon, Nicolas Robette :

le choix des coûts revient à positionner le curseur entre [deux cas limites], selon que l’on privilégie la contemporanéité des situations ou la présence de sous-séquences communes (Lesnard et de Saint Pol, 2009), la temporalité ou l’ordre au sein des trajectoires. Avec un coût de substitution unique, fixer le coût indel aux trois quarts de la valeur du coût de substitution est une solution médiane (Robette et Bry, 2012).

Avec des coûts de substitution constants et égaux à 2, la solution médiane pour le coût indel est donc de 1,5.

Le calcul de la matrice des distances s’effectue avec la fonction TraMineR::seqdist(). Nous préciserons method = "OM" pour indiquer le recours à l’optimal matching, sm = "CONSTANT" pour indiquer une matrice de substitution à coûts constants (2 par défaut) et indel = 1.5 pour fixer le coût d’insertion/suppression.

md <-
  seq |> 
  seqdist(
    method = "OM",
    sm = "CONSTANT",
    indel = 1.5
  ) |> 
  as.dist()

 [>] 500 sequences with 6 distinct states

 [>] Computing sm with seqcost using  CONSTANT

 [>] creating 6x6 substitution-cost matrix using 2 as constant value

 [>] 377 distinct  sequences 

 [>] min/max sequence lengths: 37/37

 [>] computing distances using the OM metric

 [>] elapsed time: 0.31 secs

Important

Notez l’usage de la fonction stats::as.dist(), nécessaire pour transformer la matrice renvoyée par TraMineR::seqdist() en un objet dist, le format usuel sous R pour les matrices de distance.

45.3.2 Calcul du dendrogramme

Maintenant que nous avons une matrice de distances, il nous reste à calculer le dendrogramme, avec hclust(), comme nous l’avions fait dans le chapitre sur la CAH (cf. Chapitre 43). Attention : il est impératif d’avoir bien appliqué as.dist() à l’étape précédente pour que hclust() fonctionne correctement.

arbre <-
  md |> 
  hclust(method = "ward.D2")

Nous pouvons maintenant représenter graphique notre dendrogramme.

arbre |> 
  factoextra::fviz_dend(show_labels = FALSE)

Le package seqhandbook propose une fonction intéressante seqhandbook::seq_heatmap() permettant de combiner le dendrogramme avec un tapis de séquence.

seqhandbook::seq_heatmap(seq, arbre)

45.3.3 Découpage en classes

Comme dans le cadre de la CAH, la question est de déterminer un nombre pertinent de classes à retenir. En premier lieu, nous pouvons regarder les sauts d’inertie avec la fonction guideR::plot_inertia_from_tree().

arbre |> 
  guideR::plot_inertia_from_tree()

L’un des auteurs de TraMineR, Mathias Studer, a développé le package WeightedCluster proposant plusieurs indicateurs pour comparer différents partitionnement. Pour cela, on aura recours à la fonction WeightedCluster::as.clustrange(). La fonction summary() permet d’avoir une synthèse des résultats.

clusters <- 
  WeightedCluster::as.clustrange(arbre, md, ncluster = 15)
summary(clusters, max.rank = 3)

     1. N groups     1.  stat 2. N groups     2.  stat 3. N groups     3.  stat
PBC            3   0.76239822           2   0.73248726           9   0.64722580
HG             3   0.90137147           2   0.87792460          11   0.84696319
HGSD           3   0.89896760           2   0.87529020          11   0.84200461
ASW            3   0.53943675           2   0.53446774           9   0.34815951
ASWw           3   0.54308476           2   0.53670139           9   0.36061342
CH             2 153.35216925           3  99.41152128           4  92.47088207
R2            15   0.56652273          14   0.55889755          13   0.54575815
CHsq           2 325.65615159           3 236.34076731           4 207.39987425
R2sq          15   0.79364602          14   0.78510979          13   0.77632170
HC             3   0.06073121          11   0.06157277          15   0.06641912

Une représentation graphique est également possible en appliquant plot() aux résultats. L’option norm = "zscore" permet de normaliser les valeurs des différents indicateurs afin de faciliter les comparaisons.

clusters |> 
  plot(
    norm = "zscore",
    lwd = 2
  )

Plusieurs indicateurs suggèrent ici un découpage en 3 classes.

arbre |> 
  factoextra::fviz_dend(show_labels = FALSE, k = 3)

Cependant, cela aboutirait à une très grande classe majoritaire (en rouge sur le graphique précédent) et nous perdrions en finesse d’analyse. Le graphique des sauts d’inertie suggère que les deux découpages suivants et pertinents seraient en 4 ou 6 classes. Le découpage en 6 classes aboutirait à certaines classes avec peu d’effectifs. Nous décidons donc de conserver 4 classes.

arbre |> 
  factoextra::fviz_dend(show_labels = FALSE, k = 4)

Nous pouvons récupérer notre typologie avec cutree().

typo <- arbre |> cutree(4)
typo |> head(5)

IND_001 IND_002 IND_003 IND_004 IND_005 
      1       2       3       1       1 

Le résultat est un vecteur numérique nommé. Les valeurs correspondent aux classes d’appartenance et les noms à l’identifiant des séquences. Cet identifiant a bien été conservé tout au long du processus car, au moment de la création de l’objet seq, nous avons soit passé cet identifiant à TraMineR::seqdef() soit utilisé guideR::long_to_seq().

Nous pouvons donc facilement faire un petit tableau de résultats avec une colonne pour la typologie obtenue et une colonne avec l’identifiant.

res <- 
  dplyr::tibble(
    id_ind = names(typo),
    typo = typo
  )
res

# A tibble: 500 × 2
   id_ind   typo
   <chr>   <int>
 1 IND_001     1
 2 IND_002     2
 3 IND_003     3
 4 IND_004     1
 5 IND_005     1
 6 IND_006     1
 7 IND_007     2
 8 IND_008     1
 9 IND_009     1
10 IND_010     1
# ℹ 490 more rows

Cela nous permet de récupérer, proprement, notre typologie dans notre fichier long.

d <- 
  d |> 
  left_join(res, by = "id_ind")

45.4 Représentation graphiques

Le package TraMineR fournit plusieurs fonctions graphiques pour décrire les différentes séquences. Le package ggseqplot propose les mêmes représentations graphiques mais en ayant recours à ggplot2, permettant ainsi des personnalisations additionnelles des graphiques après leur génération.

Les chronogrammes (state distribution plots) présentent une série de coupes transversales : pour chaque âge, on a les proportions d’individus de la classe dans les différentes situations. Ce graphique s’obtient avec TraMineR::seqdplot() ou ggseqplot::ggseqdplot(). Il est possible de lui passer nos classes via l’argument group afin de générer un graphique par sous-groupe.

seq |> 
  seqdplot(group = typo)

library(ggseqplot, quietly = TRUE)

ℹ ggseqplot version 0.8.9 loaded
  Website: <https://maraab23.github.io/ggseqplot/>
  Citation: `citation("ggseqplot")`

seq |> 
  ggseqdplot(group = typo)

Nous pouvons voir que la première classe est marquée par des études courtes et une carrière principalement à temps plein. La seconde classe se démarque par des études plus longues. La troisième est marquée par l’inactivité (par exemple des mères au foyer) et la quatrième par des emplois à temps partiels et/ou des petits boulots.

Les tapis de séquences (index plot) s’obtiennent avec TraMineR::seqIplot() ou ggseqplot::ggseqiplot().

seq |> seqIplot(group = typo)

seq |> ggseqiplot(group = typo)

Il est possible de trier les séquences pour rendre les tapis plus lisibles, par exemple par multidimensional scaling à l’aide de la fonction stats::cmdscale() appliquée à notre matrice de distance.

ordre <- cmdscale(md, k = 1)[, 1]
seq |> ggseqiplot(group = typo, sortv = ordre)

Cette représentation des tapis de séquence accorde la même superficie à chaque classe, indépendamment du nombre d’observations.

Une alternative consiste à avoir recours à guideR::plot_trajectories() où chaque trajectoire a la même hauteur, permettant ainsi de mieux visualiser les différences d’effectifs entre classes. En amont, nous allons récupérer la variable d’ordonnancement dans notre fichier long.

tmp <- tibble(
  id_ind = names(ordre),
  ordre = ordre
)
d <- 
  d |> 
  left_join(tmp, by = "id_ind") 

d |> 
  unlabelled() |> 
  plot_trajectories(
    id = id_ind,
    time = age,
    fill = statut_pro2,
    by = typo,
    sort_by = ordre
  )

On peut aussi visualiser avec TraMineR::seqmsplot() ou ggseqplot::ggseqmsplot() l’état modal ou modal state (celui qui correspond au plus grand nombre de séquences de la classe) à chaque âge, la hauteur des barres correspondant à la fréquence de l’état modal à chaque âge.

seq |> ggseqmsplot(group = typo)

On peut également représenter avec TraMineR::seqmtplot() ou ggseqplot::ggseqmtplot() les durées moyennes (mean time) passées dans les différents états.

seq |> ggseqmtplot(group = typo)

La distance des séquences d’une classe au centre de cette classe s’obtient avec TraMineR::disscenter(). En calculant la moyenne par classe, cela nous permet de mesurer plus précisément l’homogénéité des classes. Une classe plus homogène aura en moyenne une distance au centre de la classe plus faible.

tibble(
  diss_center = disscenter(md, group = typo),
  typo = typo
) |> 
  group_by(typo) |> 
  summarise(mean_diss = mean(diss_center))

# A tibble: 4 × 2
   typo mean_diss
  <int>     <dbl>
1     1      6.69
2     2     13.3 
3     3     14.8 
4     4     20.3 

Ici, nous voyons que la classe 1 est la plus homogène à l’inverse de la classe 4 qui est la plus hétérogène.

Les mêmes moyennes peuvent s’obtenir plus facilement avec TraMineR::dissassoc() (section Discrepancy per level dans les résultats).

dissassoc(md, typo)

Pseudo ANOVA table:
            SS  df       MSE
Exp   2847.290   3 949.09681
Res   5090.814 496  10.26374
Total 7938.104 499  15.90802

Test values  (p-values based on 1000 permutation):
                   t0 p.value
Pseudo F   92.4708821   0.001
Pseudo Fbf 63.4135413   0.001
Pseudo R2   0.3586865   0.001
Bartlett   39.4515872   0.001
Levene     63.7587160   0.001

Inconclusive intervals: 
0.00383  <  0.01  <  0.0162
0.03649  <  0.05  <  0.0635 

Discrepancy per level:
        n discrepancy
1     281    6.694887
2     118   13.254955
3      74   14.827611
4      27   20.304527
Total 500   15.876208

L’entropie transversale décrit l’évolution de l’homogénéité de la classe. Pour un âge donné, une entropie proche de 0 signifie que tous les individus de la classe (ou presque) sont dans la même situation. À l’inverse, l’entropie est de 1 si les individus sont dispersés dans toutes les situations. Ce type de graphique produit par TraMineR::seqHtplot() ou ggseqplot::ggseqeplot() peut être pratique pour localiser les moments de transition.

seq |> seqHtplot(group = typo)

seq |> ggseqeplot(group = typo)

45.5 Étapes suivantes

Assez classiquement, on souhaitera analyser si chaque classe est associée à certaines caractéristiques sociodémographiques (ou autres) que l’on connaîtrait sur les individus.

On retombe ici sur la stastistique descriptive bivariée classique (cf. Chapitre 19) et éventuellement sur une régression logistique multinomiale (cf. Chapitre 46).

45.6 webin-R

L’analyse de séquences est présentée sur YouTube dans le webin-R #16 (Analyse de séquences).

45.7 Lectures complémentaires

• L’analyse statistique des trajectoires par Nicolas Robette, Collection : Méthodes et savoirs n°12, éditions de l’Ined, 2021 (accès freemium).

• Tutoriel d’analyse de séquences par Nicolas Robette (doi : 10.34847/nkl.bdccx20o)

• L’analyse de séquences : une introduction avec le logiciel R et le package TraMineR, par Nicolas Robette, carnet Quanti sur Hyoptheses.org, 2012.

• Explorer et décrire les parcours de vie : les typologies de trajectoires par Nicolas Robette, collection Les clefs pour, éditions du Ceped, 2011 (en accès libre).

• Mining sequence data in R with the TraMineR package: A user’s guide par Alexis Gabadinho, Gilbert Ritschard, Matthias Studer and Nicolas S. Müller. Il s’agit du guide d’utilisation officiel de TraMineR et il constitue une solide introduction à l’analyse de séquences.

• “What Matters in Differences Between Life Trajectories: A Comparative Review of Sequence Dissimilarity Measures Open Access” par Matthias Studer et Gilbert Ritschard, Journal of the Royal Statistical Society Series A: Statistics in Society, Volume 179, Issue 2, February 2016, Pages 481–511, https://doi.org/10.1111/rssa.12125.