Régression logistique binaire, multinomiale et ordinale
Une version actualisée de ce chapitre est disponible sur guide-R : Régression logistique binaire. Voir également Sélection pas à pas d’un modèle, Régression logistique multinomiale, Régression logistique ordinale et Régression logistique binaire pondérée.
La version originale de ce chapitre a été écrite par Joseph Larmarange dans le cadre du support de cours Introduction à l’analyse d’enquêtes avec R.
Ce chapitre est évoqué dans le webin-R #06 (régression logistique partie 1) sur YouTube.
Ce chapitre est évoqué dans le webin-R #07 (régression logistique partie 2) sur YouTube.
Ce chapitre est évoqué dans le webin-R #20 (trajectoires de soins : un exemple de données longitudinales 4 : régression logistique multinomiale & modèles mixtes à classe latente) sur YouTube.
Ce chapitre est évoqué dans le webin-R #21 (trajectoires de soins : un exemple de données longitudinales 5 : modèle à observations répétée, régression logistique ordinale GEE & analyse de survie multi-états) sur YouTube.
La régression logistique est fréquemment utilisée en sciences sociales car elle permet d’effectuer un raisonnement dit toutes choses étant égales par ailleurs. Plus précisément, la régression logistique a pour but d’isoler les effets de chaque variable, c’est-à-dire d’identifier les effets résiduels d’une variable explicative sur une variable d’intérêt, une fois pris en compte les autres variables explicatives introduites dans le modèle. La régression logistique est ainsi prisée en épidémiologie pour identifier les facteurs associés à telle ou telle pathologie.
La régression logistique ordinaire ou régression logistique binaire vise à expliquer une variable d’intérêt binaire (c’est-à-dire de type « oui / non » ou « vrai / faux »). Les variables explicatives qui seront introduites dans le modèle peuvent être quantitatives ou qualitatives.
La régression logistique multinomiale est une extension de la régression logistique aux variables qualitatives à trois modalités ou plus, la régression logistique ordinale aux variables qualitatives à trois modalités ou plus qui sont ordonnées hiérarchiquement.
Préparation des données
Dans ce chapite, nous allons encore une fois utiliser les données de l’enquête Histoire de vie, fournies avec l’extension questionr.
À titre d’exemple, nous allons étudier l’effet de l’âge, du sexe, du niveau d’étude, de la pratique religieuse et du nombre moyen d’heures passées à regarder la télévision par jour sur le fait de pratiquer un sport.
En premier lieu, il importe de vérifier que notre variable d’intérêt (ici sport) est correctement codée. Une possibilité consiste à créer une variable booléenne (vrai / faux) selon que l’individu a pratiqué du sport ou non :
Dans le cas présent, cette variable n’a pas de valeur manquante. Mais, le cas échéant, il importe de bien coder les valeurs manquantes en NA, les individus en question étant alors exclu de l’analyse.
Il n’est pas forcément nécessaire de transformer notre variable d’intérêt en variable booléenne. En effet, R accepte sans problème une variable de type facteur. Cependant, l’ordre des valeurs d’un facteur a de l’importance. En effet, R considère toujours la première modalité comme étant la modalité de référence. Dans le cas de la variable d’intérêt, la modalité de référence correspond au fait de ne pas remplir le critère étudié, dans notre exemple au fait de ne pas avoir eu d’activité sportive au cours des douze derniers mois.
Pour connaître l’ordre des modalités d’une variable de type facteur, on peut utiliser la fonction levels ou bien encore tout simplement la fonction freq de l’extension questionr :
[1] "Non" "Oui"Dans notre exemple, la modalité « Non » est déjà la première modalité. Il n’y a donc pas besoin de modifier notre variable. Si ce n’est pas le cas, il faudra modifier la modalité de référence avec la fonction fct_relevel ou la fonction relevel comme nous allons le voir un peu plus loin.
Il est possible d’indiquer un facteur à plus de deux modalités. Dans une telle situation, R considérera que tous les modalités, sauf la modalité de référence, est une réalisation de la variable d’intérêt. Cela serait correct, par exemple, si notre variable sport était codée ainsi : « Non », « Oui, toutes les semaines », « Oui, au moins une fois par mois », « Oui, moins d’une fois par mois ». Cependant, afin d’éviter tout risque d’erreur ou de mauvaise interprétation, il est vivement conseillé de recoder au préalable sa variable d’intérêt en un facteur à deux modalités.
La notion de modalité de référence s’applique également aux variables explicatives qualitatives. En effet, dans un modèle, tous les coefficients sont calculés par rapport à la modalité de référence. Il importe de choisir une modalité de référence qui fasse sens afin de faciliter l’interprétation. Par ailleurs, ce choix peut également dépendre de la manière dont on souhaite présenter les résultats. De manière générale on évitera de choisir comme référence une modalité peu représentée dans l’échantillon ou bien une modalité correspondant à une situation atypique.
Prenons l’exemple de la variable sexe. Souhaite-t-on connaitre l’effet d’être une femme par rapport au fait d’être un homme ou bien l’effet d’être un homme par rapport au fait d’être une femme ? Si l’on opte pour le second, alors notre modalité de référence sera le sexe féminin. Comme est codée cette variable ?
La modalité « Femme » s’avère ne pas être la première modalité. Nous devons appliquer la fonction fct_relevel ou la fonction relevel :
Données labellisées
Si l’on utilise des données labellisées (voir le chapitre dédié), nos variables catégorielles seront stockées sous la forme d’un vecteur numérique avec des étiquettes. Il sera donc nécessaire de convertir ces variables en facteurs, tout simplement avec la fonction to_factor de l’extension labelled qui pourra utiliser les étiquettes de valeurs comme modalités du facteur.
Les variables age et heures.tv sont des variables quantitatives. Il importe de vérifier qu’elles sont bien enregistrées en tant que variables numériques. En effet, il arrive parfois que dans le fichier source les variables quantitatives soient renseignées sous forme de valeur textuelle et non sous forme numérique.
int [1:2000] 28 23 59 34 71 35 60 47 20 28 ... num [1:2000] 0 1 0 2 3 2 2.9 1 2 2 ...Nos deux variables sont bien renseignées sous forme numérique.
Cependant, l’effet de l’âge est rarement linéaire. Un exemple trivial est par exemple le fait d’occuper un emploi qui sera moins fréquent aux jeunes âges et aux âges élevés. Dès lors, on pourra transformer la variable age en groupe d’âges avec la fonction cut (voir le chapitre Manipulation de données) :
Jetons maintenant un oeil à la variable nivetud :
En premier lieu, cette variable est détaillée en pas moins de huit modalités dont certaines sont peu représentées (seulement 39 individus soit 2 % n’ont jamais fait d’études par exemple). Afin d’améliorier notre modèle logistique, il peut être pertinent de regrouper certaines modalités (voir le chapitre Manipulation de données) :
d$etud <- d$nivetud
levels(d$etud) <- c(
"Primaire", "Primaire", "Primaire",
"Secondaire", "Secondaire", "Technique/Professionnel",
"Technique/Professionnel", "Supérieur"
)
freq(d$etud)Notre variable comporte également 112 individus avec une valeur manquante. Si nous conservons cette valeur manquante, ces 112 individus seront, par défaut, exclus de l’analyse. Ces valeurs manquantes n’étant pas négligeable (5,6 %), nous pouvons également faire le choix de considérer ces valeurs manquantes comme une modalité supplémentaire. Auquel cas, nous utiliserons la fonction fct_explicit_na fournie par questionr1 :
[1] "Primaire" "Secondaire"
[3] "Technique/Professionnel" "Supérieur" [1] "Primaire" "Secondaire"
[3] "Technique/Professionnel" "Supérieur"
[5] "manquant" Régression logistique binaire
La fonction glm (pour generalized linear models soit modèle linéaire généralisé en français) permet de calculer une grande variété de modèles statistiques. La régression logistique ordinaire correspond au modèle logit de la famille des modèles binomiaux, ce que l’on indique à glm avec l’argument family=binomial(logit).
Le modèle proprement dit sera renseigné sous la forme d’une formule (que nous avons déjà rencontrée dans le chapitre sur la statistique bivariée et présentée plus en détails dans un chapitre dédié). On indiquera d’abord la variable d’intérêt, suivie du signe ~ (que l’on obtient en appuyant sur les touches Alt Gr et 3 sur un clavier de type PC) puis de la liste des variables explicatives séparées par un signe +. Enfin, l’argument data permettra d’indiquer notre tableau de données.
reg <- glm(sport ~ sexe + grpage + etud + relig + heures.tv, data = d, family = binomial(logit))
reg
Call: glm(formula = sport ~ sexe + grpage + etud + relig + heures.tv,
family = binomial(logit), data = d)
Coefficients:
(Intercept)
-0.7984
sexeHomme
0.4397
grpage[25,45)
-0.4204
grpage[45,65)
-1.0854
grpage[65,99]
-1.3814
etudSecondaire
0.9506
etudTechnique/Professionnel
1.0493
etudSupérieur
1.8917
etudmanquant
2.1504
religPratiquant occasionnel
-0.0219
religAppartenance sans pratique
-0.0067
religNi croyance ni appartenance
-0.2154
religRejet
-0.3835
religNSP ou NVPR
-0.0838
heures.tv
-0.1209
Degrees of Freedom: 1994 Total (i.e. Null); 1980 Residual
(5 observations effacées parce que manquantes)
Null Deviance: 2610
Residual Deviance: 2210 AIC: 2240Il est possible de spécifier des modèles plus complexes. Par exemple, x:y permet d’indiquer l’interaction entre les variables x et y. x * y sera équivalent à x + y + x:y. Pour aller plus loin, voir http://ww2.coastal.edu/kingw/statistics/R-tutorials/formulae.html.
Une présentation plus complète des résultats est obtenue avec la méthode summary :
Call:
glm(formula = sport ~ sexe + grpage + etud + relig + heures.tv,
family = binomial(logit), data = d)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.878 -0.886 -0.481 1.003 2.422
Coefficients:
Estimate Std. Error
(Intercept) -0.7984 0.3239
sexeHomme 0.4397 0.1061
grpage[25,45) -0.4204 0.2281
grpage[45,65) -1.0854 0.2377
grpage[65,99] -1.3814 0.2738
etudSecondaire 0.9506 0.1974
etudTechnique/Professionnel 1.0493 0.1898
etudSupérieur 1.8917 0.1952
etudmanquant 2.1504 0.3302
religPratiquant occasionnel -0.0219 0.1892
religAppartenance sans pratique -0.0067 0.1747
religNi croyance ni appartenance -0.2154 0.1931
religRejet -0.3835 0.2859
religNSP ou NVPR -0.0838 0.4110
heures.tv -0.1209 0.0336
z value Pr(>|z|)
(Intercept) -2.46 0.01371 *
sexeHomme 4.15 3.4e-05 ***
grpage[25,45) -1.84 0.06524 .
grpage[45,65) -4.57 5.0e-06 ***
grpage[65,99] -5.05 4.5e-07 ***
etudSecondaire 4.81 1.5e-06 ***
etudTechnique/Professionnel 5.53 3.2e-08 ***
etudSupérieur 9.69 < 2e-16 ***
etudmanquant 6.51 7.4e-11 ***
religPratiquant occasionnel -0.12 0.90783
religAppartenance sans pratique -0.04 0.96943
religNi croyance ni appartenance -1.12 0.26462
religRejet -1.34 0.17976
religNSP ou NVPR -0.20 0.83847
heures.tv -3.60 0.00032 ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2609.2 on 1994 degrees of freedom
Residual deviance: 2206.2 on 1980 degrees of freedom
(5 observations effacées parce que manquantes)
AIC: 2236
Number of Fisher Scoring iterations: 4Coefficients du modèle
Dans le cadre d’un modèle logistique, généralement on ne présente pas les coefficients du modèle mais leur valeur exponentielle, cette dernière correspondant en effet à des odds ratio, également appelés rapports des cotes. L’odds ratio diffère du risque relatif. Cependent son interprétation est similaire. Un odds ratio de 1 signifie l’absence d’effet. Un odds ratio largement supérieur à 1 correspond à une augmentation du phénomène étudié et un odds ratio largement inféieur à 1 correspond à une diminution du phénomène étudié2.
La fonction coef permet d’obtenir les coefficients d’un modèle, confint leurs intervalles de confiance et exp de calculer l’exponentiel. Les odds ratio et leurs intervalles de confiance s’obtiennent ainsi :
(Intercept)
0.4501
sexeHomme
1.5522
grpage[25,45)
0.6568
grpage[45,65)
0.3378
grpage[65,99]
0.2512
etudSecondaire
2.5872
etudTechnique/Professionnel
2.8555
etudSupérieur
6.6304
etudmanquant
8.5885
religPratiquant occasionnel
0.9783
religAppartenance sans pratique
0.9933
religNi croyance ni appartenance
0.8062
religRejet
0.6814
religNSP ou NVPR
0.9196
heures.tv
0.8861 Attente de la réalisation du profilage... 2.5 % 97.5 %
(Intercept) 0.2377 0.8473
sexeHomme 1.2614 1.9120
grpage[25,45) 0.4194 1.0275
grpage[45,65) 0.2115 0.5381
grpage[65,99] 0.1464 0.4288
etudSecondaire 1.7653 3.8328
etudTechnique/Professionnel 1.9805 4.1729
etudSupérieur 4.5518 9.7951
etudmanquant 4.5348 16.5885
religPratiquant occasionnel 0.6759 1.4199
religAppartenance sans pratique 0.7063 1.4020
religNi croyance ni appartenance 0.5524 1.1782
religRejet 0.3869 1.1890
religNSP ou NVPR 0.3997 2.0216
heures.tv 0.8290 0.9458On pourra faciliter la lecture en combinant les deux :
Attente de la réalisation du profilage... 2.5 % 97.5 %
(Intercept) 0.4501 0.2377 0.8473
sexeHomme 1.5522 1.2614 1.9120
grpage[25,45) 0.6568 0.4194 1.0275
grpage[45,65) 0.3378 0.2115 0.5381
grpage[65,99] 0.2512 0.1464 0.4288
etudSecondaire 2.5872 1.7653 3.8328
etudTechnique/Professionnel 2.8555 1.9805 4.1729
etudSupérieur 6.6304 4.5518 9.7951
etudmanquant 8.5885 4.5348 16.5885
religPratiquant occasionnel 0.9783 0.6759 1.4199
religAppartenance sans pratique 0.9933 0.7063 1.4020
religNi croyance ni appartenance 0.8062 0.5524 1.1782
religRejet 0.6814 0.3869 1.1890
religNSP ou NVPR 0.9196 0.3997 2.0216
heures.tv 0.8861 0.8290 0.9458Pour savoir si un odds ratio diffère significativement de 1 (ce qui est identique au fait que le coefficient soit différent de 0), on pourra se référer à la colonne Pr(>|z|) obtenue avec summary.
Si vous disposez de l’extension questionr, la fonction odds.ratio permet de calculer directement les odds ratio, leur intervalles de confiance et les p-value :
Attente de la réalisation du profilage...La fonction tidy de l’extension broom pour récupérer les coefficients du modèle sous la forme d’un tableau de données. On précisera conf.int = TRUE pour obtenir les intervalles de confiance et exponentiate = TRUE pour avoir les odds ratio plutôt que les coefficients bruts.
L’extension broom.helpers fournit une fonction tidi_plus_plus qui permet d’améliorer le tableau renvoyé par tidy en y identifiant les variables utilisés, ajoutant les modalités de référence et en proposant des étiquettes plus explicites.
Attachement du package : 'broom.helpers'Les objets suivants sont masqués depuis 'package:gtsummary':
all_continuous, all_contrastsSi l’on souhaite avoir des noms de variables plus explicites, il faut ajouter des étiquettes des variables avec var_label de l’extension labelled (voir le chapitre sur les vecteurs labellisés).
Par contre, cette étape doit avoir eu lieu avant le calcul de la régression linéaire.
library(labelled)
var_label(d$sport) <- "Pratique du sport ?"
var_label(d$sexe) <- "Sexe"
var_label(d$grpage) <- "Groupe d'âges"
var_label(d$etud) <- "Niveau d'étude"
var_label(d$relig) <- "Pratique religieuse"
var_label(d$heures.tv) <- "Heures de télévision / jour"
var_label(d$trav.imp) <- "Importance du travail"
reg <- glm(sport ~ sexe + grpage + etud + relig + heures.tv, data = d, family = binomial(logit))La fonction tbl_regression de l’extension gtsummary, qui a recours en interne à broom.helpers, permet d’obtenir un tableau plus propre. Comme nous souhaitons afficher les odds ratios plutôt que les coefficients du modèle, on indiquera exponentiate = TRUE.
| Caractéristique | OR1 | 95% IC1 | p-valeur |
|---|---|---|---|
| Sexe | |||
| Femme | — | — | |
| Homme | 1,55 | 1,26 – 1,91 | <0,001 |
| Groupe d'âges | |||
| [16,25) | — | — | |
| [25,45) | 0,66 | 0,42 – 1,03 | 0,065 |
| [45,65) | 0,34 | 0,21 – 0,54 | <0,001 |
| [65,99] | 0,25 | 0,15 – 0,43 | <0,001 |
| Niveau d'étude | |||
| Primaire | — | — | |
| Secondaire | 2,59 | 1,77 – 3,83 | <0,001 |
| Technique/Professionnel | 2,86 | 1,98 – 4,17 | <0,001 |
| Supérieur | 6,63 | 4,55 – 9,80 | <0,001 |
| manquant | 8,59 | 4,53 – 16,6 | <0,001 |
| Pratique religieuse | |||
| Pratiquant regulier | — | — | |
| Pratiquant occasionnel | 0,98 | 0,68 – 1,42 | >0,9 |
| Appartenance sans pratique | 0,99 | 0,71 – 1,40 | >0,9 |
| Ni croyance ni appartenance | 0,81 | 0,55 – 1,18 | 0,3 |
| Rejet | 0,68 | 0,39 – 1,19 | 0,2 |
| NSP ou NVPR | 0,92 | 0,40 – 2,02 | 0,8 |
| Heures de télévision / jour | 0,89 | 0,83 – 0,95 | <0,001 |
| 1 OR = rapport de cotes, IC = intervalle de confiance | |||
On pourra se référer à la vignette dédiée (en anglais) pour découvrir les différentes options de tbl_regression.
Représentation graphique du modèle
Il est possible de représenter graphiquement les différents odds ratios avec la fonction ggcoef_model de GGally.
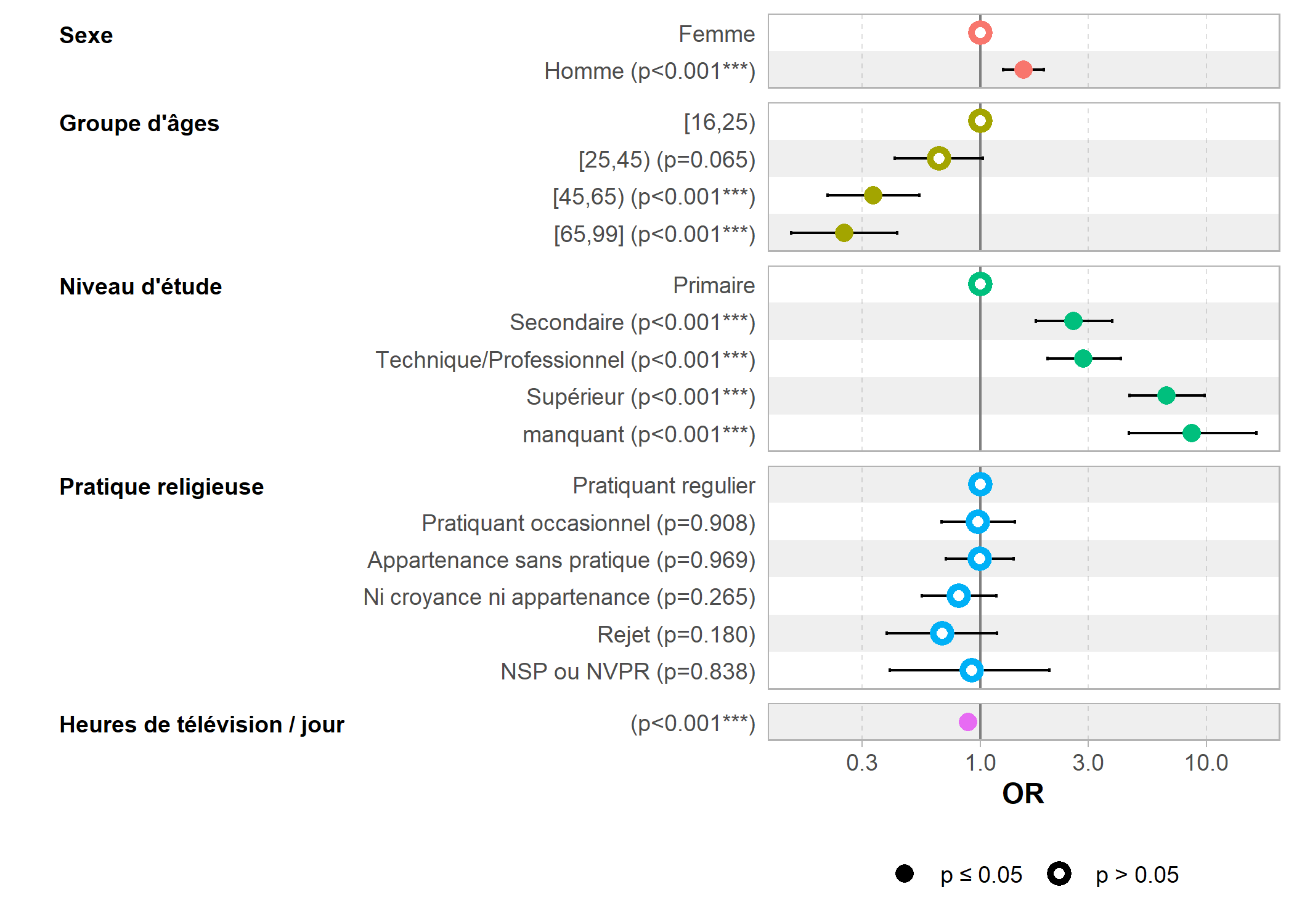
L’extension forestmodel propose de son côté une fonction forest_model qui, à partir d’un modèle, propose une représentation visuelle et tabulaire des coefficients.
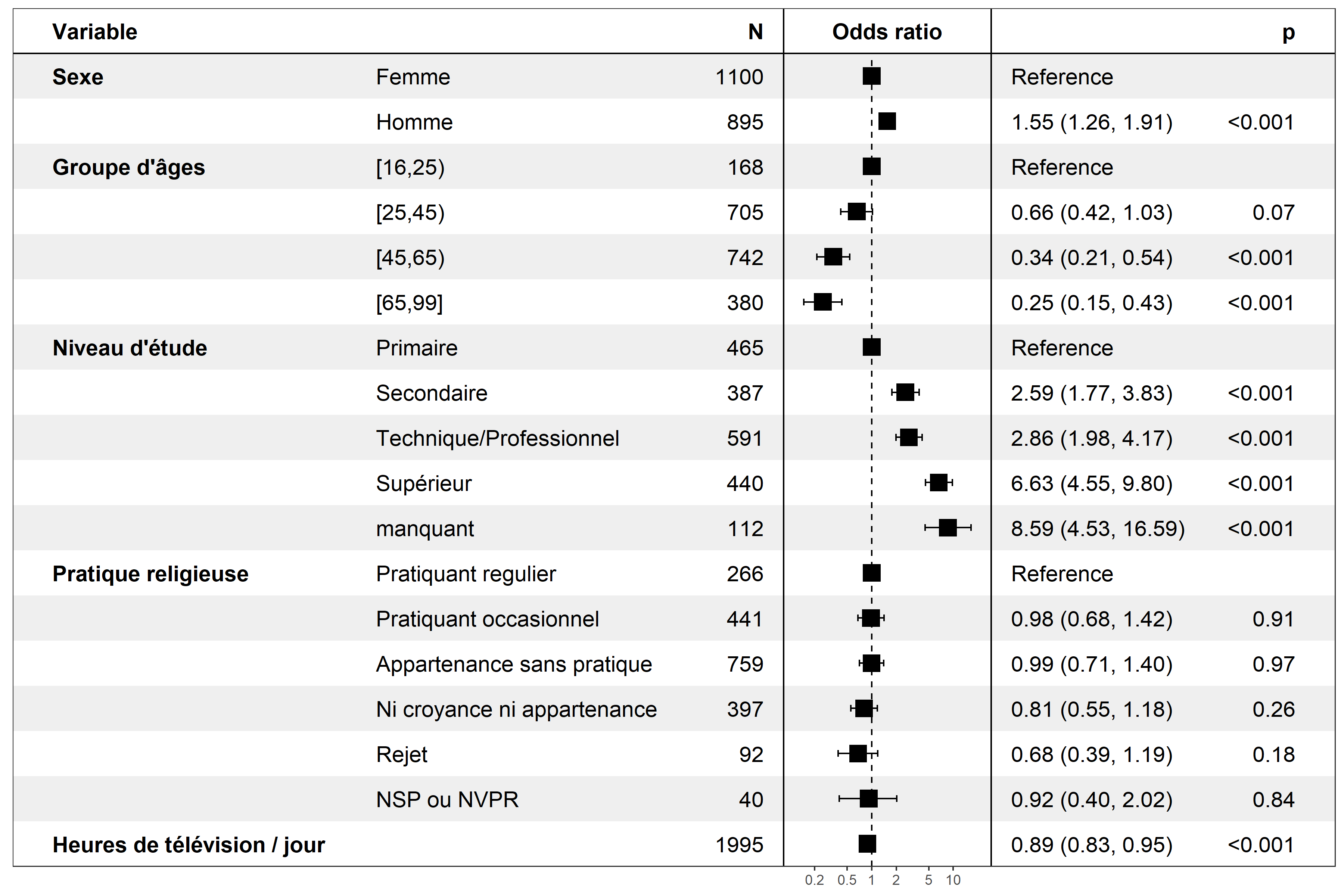
A la différence de ggcoef_model qui fonctionne avec la plupart des types de modèles (dont les modèles à effets mixtes ou ceux réalisés avec un plan d’échantillonnage complexe), forest_model ne fonctionne qu’avec les modèles les plus courants.
Représentation graphique des effets
Une version actualisée de cette section est disponible sur guide-R : Prédictions marginales, contrastes marginaux & effets marginaux
L’extension effects propose une représentation graphique résumant les effets de chaque variable du modèle. Pour cela, il suffit d’appliquer la méthode plot au résultat de la fonction allEffects. Nous obtenons alors la figure ci-dessous.
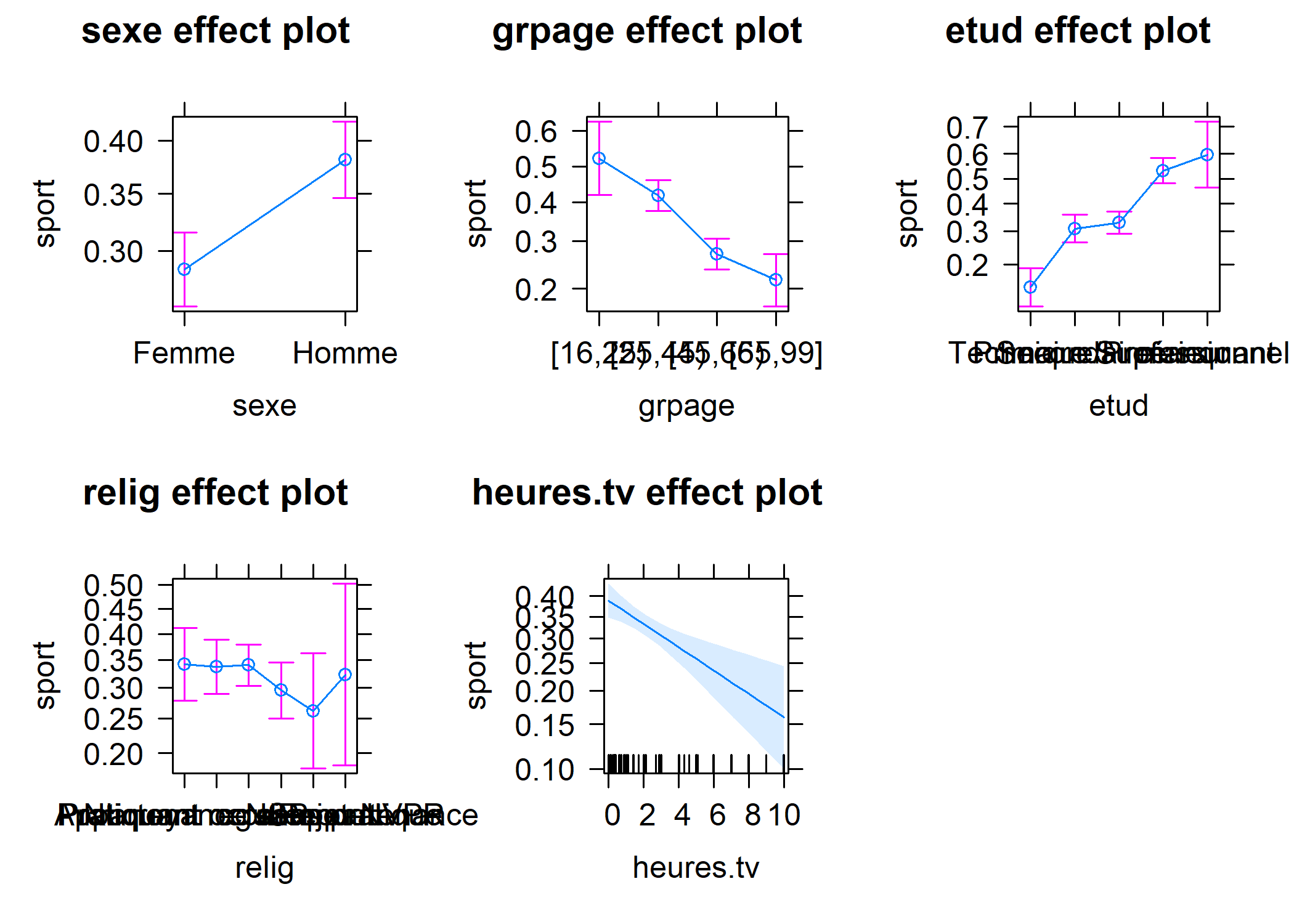
Nous pouvons alternativement avoir recours à l’extension ggeffects3 et sa fonction ggeffect qui permettent de récupérer les résultats de effects dans un format utilisable avec ggplot2.
Ainsi, la fonction ggeffect, quand on lui précise un terme spécifique, produit un tableau de données avec les effets marginaux pour cette variable.
En combinant ce résultat avec plot, on obtient un graphique ggplot2 de l’effet en question.
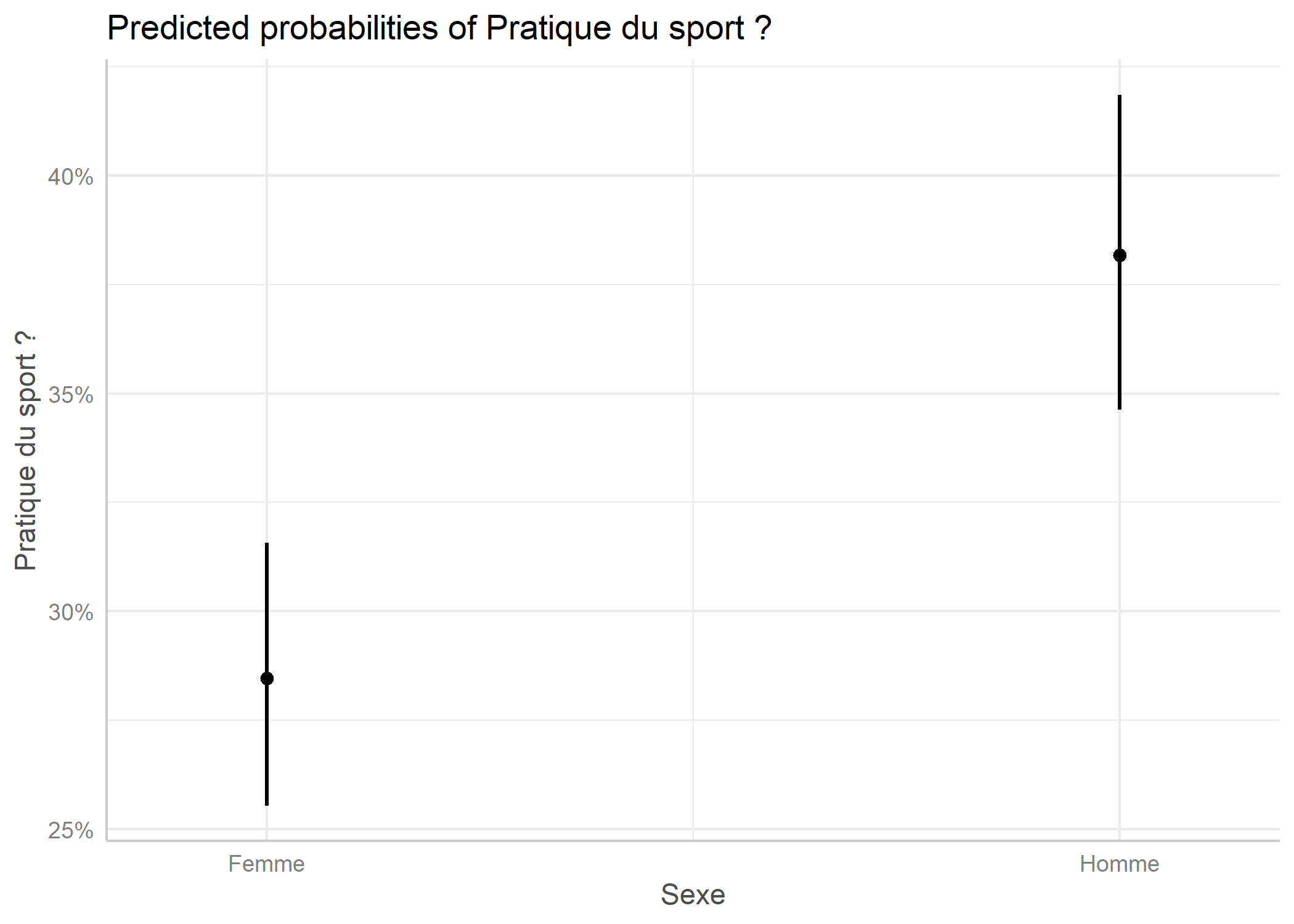
Si l’on ne précise pas de terme, ggeffect(reg) calcule les effets pour chaque variable du modèle et plot(ggeffect(reg)) renvoie une liste de graphiques. Il faut donc utiliser la fonction plot_grid de cowplot pour combiner ces graphiques en un seul (voir le chapitre dédié).
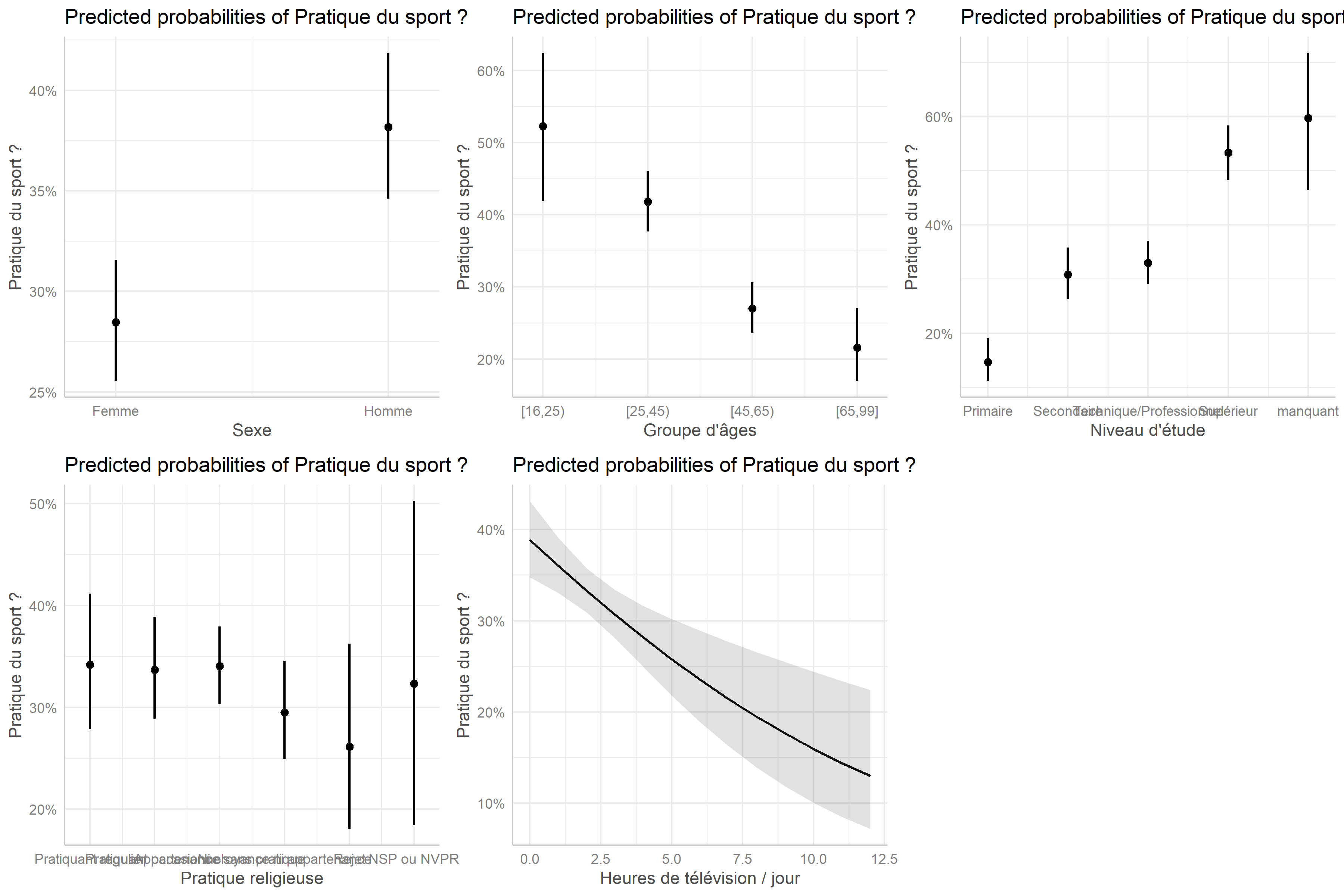
On pourra noter la prise en compte par ggeffect des étiquettes de variables définies plus haut.
Matrice de confusion
Une manière de tester la qualité d’un modèle est le calcul d’une matrice de confusion, c’est-à-dire le tableau croisé des valeurs observées et celles des valeurs prédites en appliquant le modèle aux données d’origine.
La méthode predict avec l’argument type="response" permet d’appliquer notre modèle logistique à un tableau de données et renvoie pour chaque individu la probabilité qu’il ait vécu le phénomène étudié.
1 2 3 4 5 6
0.61241 0.73415 0.15983 0.70350 0.07294 0.34824 Or notre variable étudiée est de type binaire. Nous devons donc transformer nos probabilités prédites en une variable du type « oui / non ». Usuellement, les probabilités prédites seront réunies en deux groupes selon qu’elles soient supérieures ou inférieures à la moitié. La matrice de confusion est alors égale à :
Non Oui
FALSE 1076 384
TRUE 199 336Nous avons donc 583 (384+199) prédictions incorrectes sur un total de 1993, soit un taux de mauvais classement de 29,3 %.
Identifier les variables ayant un effet significatif
Les p-values associées aux odds ratios nous indique si un odd ratio est significativement différent de 1, par rapport à la modalité de référence. Mais cela n’indique pas si globalement une variable a un effet significatif sur le modèle. Pour tester l’effet global sur un modèle, on peut avoir recours à la fonction drop1. Cette dernière va tour à tour supprimer chaque variable du modèle et réaliser une analyse de variance (ANOVA, voir fonction anova) pour voir si la variance change significativement.
Ainsi, dans le cas présent, la suppression de la variable relig ne modifie significativement pas le modèle, indiquant l’absence d’effet de cette variable.
Une fonction plus générique (i.e. fonctionnant avec une plus grande variété de modèles) est la fonction Anova de l’extension car.
Si l’on a recours à tbl_regression, on peut facilement ajouter les p-valeurs globales avec add_global_p.
| Caractéristique | OR1 | 95% IC1 | p-valeur |
|---|---|---|---|
| Sexe | <0,001 | ||
| Femme | — | — | |
| Homme | 1,55 | 1,26 – 1,91 | |
| Groupe d'âges | <0,001 | ||
| [16,25) | — | — | |
| [25,45) | 0,66 | 0,42 – 1,03 | |
| [45,65) | 0,34 | 0,21 – 0,54 | |
| [65,99] | 0,25 | 0,15 – 0,43 | |
| Niveau d'étude | <0,001 | ||
| Primaire | — | — | |
| Secondaire | 2,59 | 1,77 – 3,83 | |
| Technique/Professionnel | 2,86 | 1,98 – 4,17 | |
| Supérieur | 6,63 | 4,55 – 9,80 | |
| manquant | 8,59 | 4,53 – 16,6 | |
| Pratique religieuse | 0,5 | ||
| Pratiquant regulier | — | — | |
| Pratiquant occasionnel | 0,98 | 0,68 – 1,42 | |
| Appartenance sans pratique | 0,99 | 0,71 – 1,40 | |
| Ni croyance ni appartenance | 0,81 | 0,55 – 1,18 | |
| Rejet | 0,68 | 0,39 – 1,19 | |
| NSP ou NVPR | 0,92 | 0,40 – 2,02 | |
| Heures de télévision / jour | 0,89 | 0,83 – 0,95 | <0,001 |
| 1 OR = rapport de cotes, IC = intervalle de confiance | |||
Concernant le test réalisé dans le cadre d’une Anova, il existe trois tests différents que l’on présente comme le type 1, le type 2 et le type 3 (ou I, II et III). Pour une explication sur ces différents types, on pourra se référer (en anglais) à https://mcfromnz.wordpress.com/2011/03/02/anova-type-iiiiii-ss-explained/ ou encore http://md.psych.bio.uni-goettingen.de/mv/unit/lm_cat/lm_cat_unbal_ss_explained.html.
Le type I n’est pas recommandé dans le cas présent car il dépend de l’ordre dans lequel les différentes variables sont testées.
Lorsqu’il n’y a pas d’interaction dans un modèle (voir le chapitre sur les interactions), le type II serait à privilégier car plus puissant.
En présence d’interactions, il est conseillé d’avoir plutôt recours au type III. Cependant, en toute rigueur, pour utiliser le type III, il faut que les variables catégorielles soient codées en utilisant un contrastes dont la somme est nulle (un contrast de type somme ou polynomial). Or, par défaut, les variables catégorielles sont codées avec un contraste de type traitement
(pour une explication sur les contrastes dans les modèles, voir en anglais cette page ou celle-ci).
Par défaut, Anova utilise le type II et add_global_p le type III. Dans les deux cas, il est possible de préciser le type de test avec type = "II" ou type = "III".
Dans le cas de notre exemple, un modèle simple sans interaction, le type de test ne change pas les résultats.
Sélection de modèles
Il est toujours tentant lorsque l’on recherche les facteurs associés à un phénomène d’inclure un nombre important de variables explicatives potentielles dans un mmodèle logistique. Cependant, un tel modèle n’est pas forcément le plus efficace et certaines variables n’auront probablement pas d’effet significatif sur la variable d’intérêt.
Pour une présentation didactique du cadre théorique de la sélection de modèle, vous pouvez consulter en ligne le cours de L. Rouvière sur la sélection/validation de modèles.
La technique de sélection descendante pas à pas est une approche visant à améliorer son modèle explicatif4. On réalise un premier modèle avec toutes les variables spécifiées, puis on regarde s’il est possible d’améliorer le modèle en supprimant une des variables du modèle. Si plusieurs variables permettent d’améliorer le modèle, on supprimera la variable dont la suppression améliorera le plus le modèle. Puis on recommence le même procédé pour voir si la suppression d’une seconde variable peut encore améliorer le modèle et ainsi de suite. Lorsque le modèle ne peut plus être améliorer par la suppresion d’une variable, on s’arrête.
Il faut également définir un critère pour déterminer la qualité d’un modèle. L’un des plus utilisés est le Akaike Information Criterion ou AIC. Plus l’AIC sera faible, meilleure sera le modèle.
La fonction step permet justement de sélectionner le meilleur modèle par une procédure pas à pas descendante basée sur la minimisation de l’AIC. La fonction affiche à l’écran les différentes étapes de la sélection et renvoie le modèle final.
Start: AIC=2236
sport ~ sexe + grpage + etud + relig + heures.tv
Df Deviance AIC
- relig 5 2210 2230
<none> 2206 2236
- heures.tv 1 2220 2248
- sexe 1 2223 2251
- grpage 3 2259 2283
- etud 4 2330 2352
Step: AIC=2230
sport ~ sexe + grpage + etud + heures.tv
Df Deviance AIC
<none> 2210 2230
- heures.tv 1 2224 2242
- sexe 1 2226 2244
- grpage 3 2261 2275
- etud 4 2334 2346Le modèle initial a un AIC de 2235,9. À la première étape, il apparait que la suppression de la variable religion permet diminuer l’AIC à 2230,2. Lors de la seconde étape, toute suppression d’une autre variable ferait augmenter l’AIC. La procédure s’arrête donc.
Pour obtenir directement l’AIC d’un modèle donné, on peut utiliser la fonction AIC.
[1] 2236[1] 2230On peut effectuer une analyse de variance ou ANOVA pour comparer les deux modèles avec la fonction anova.
Il n’y a pas de différences significatives entre nos deux modèles. Autrement dit, notre second modèle explique tout autant de variance que notre premier modèle, tout en étant plus parcimonieux.
Une alternative à la fonction step est la fonction stepAIC de l’extension MASS qui fonctionne de la même manière. Si cela ne change rien aux régressions logistiques classiques, il arrive que pour certains types de modèle la méthode step ne soit pas disponible, mais que stepAIC puisse être utilisée à la place.
Start: AIC=2236
sport ~ sexe + grpage + etud + relig + heures.tv
Df Deviance AIC
- relig 5 2210 2230
<none> 2206 2236
- heures.tv 1 2220 2248
- sexe 1 2223 2251
- grpage 3 2259 2283
- etud 4 2330 2352
Step: AIC=2230
sport ~ sexe + grpage + etud + heures.tv
Df Deviance AIC
<none> 2210 2230
- heures.tv 1 2224 2242
- sexe 1 2226 2244
- grpage 3 2261 2275
- etud 4 2334 2346Un critère similaire à l’AIC est le critère BIC (Bayesian Information Criterion) appelé aussi SBC (Schwarz information criterion). Il s’obtient avec step an ajoutant l’argument k = log(n) où n est le nombre d’observations inclues dans le modèle que l’on peut obtenir avec nrow(model.matrix(reg)) (pour tenir compte des éventuelles observations manquantes retirées des données pour le calcul du modèle).
Start: AIC=2320
sport ~ sexe + grpage + etud + relig + heures.tv
Df Deviance AIC
- relig 5 2210 2286
<none> 2206 2320
- heures.tv 1 2220 2326
- sexe 1 2223 2330
- grpage 3 2259 2350
- etud 4 2330 2414
Step: AIC=2286
sport ~ sexe + grpage + etud + heures.tv
Df Deviance AIC
<none> 2210 2286
- heures.tv 1 2224 2292
- sexe 1 2226 2295
- grpage 3 2261 2314
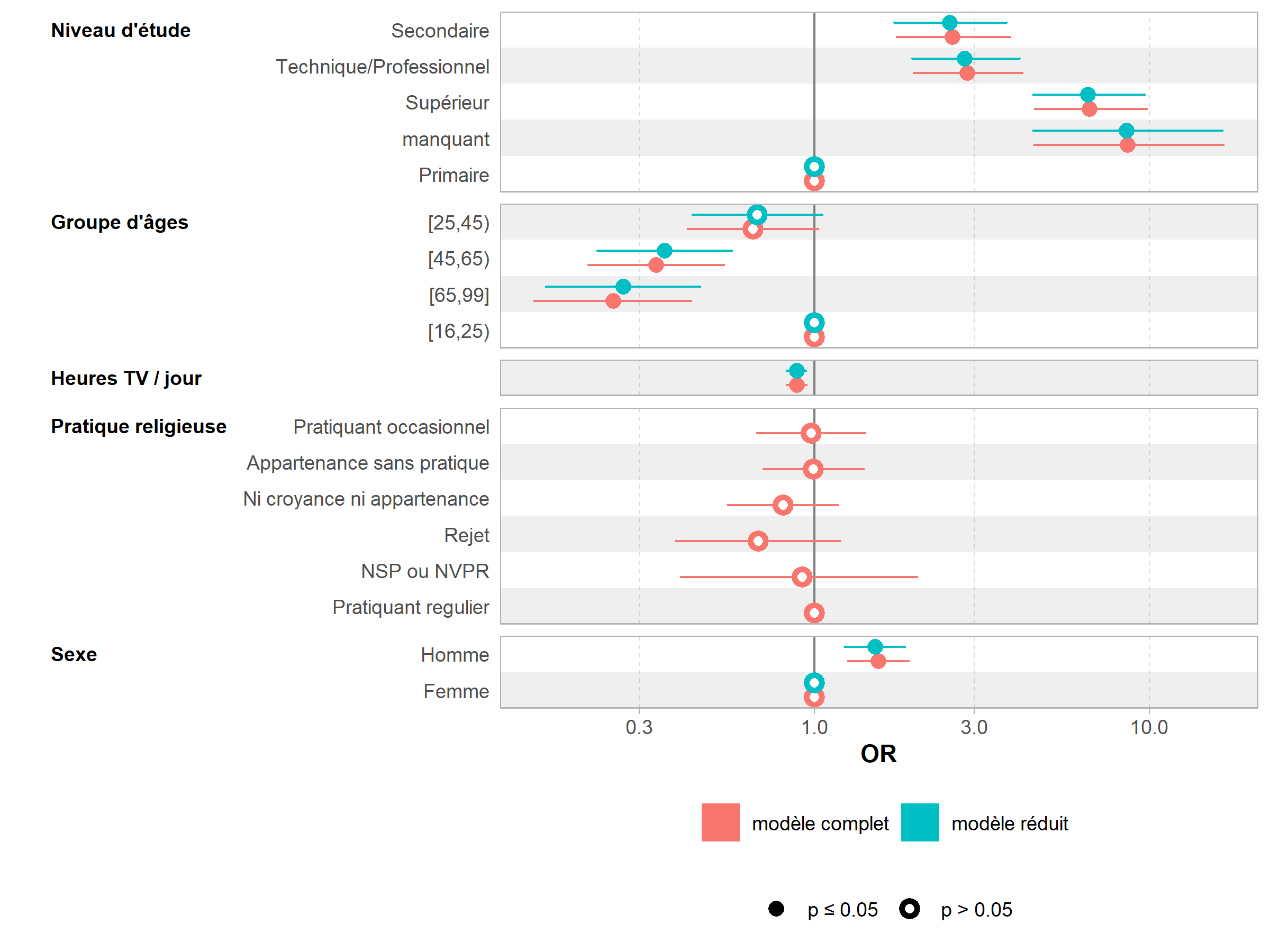
- etud 4 2334 2380On peut facilement comparer visuellement deux modèles avec ggcoef_compare de GGally.
library(GGally)
ggcoef_compare(
list("modèle complet" = reg, "modèle réduit" = reg2),
exponentiate = TRUE,
variable_labels = c(heures.tv = "Heures TV / jour")
)
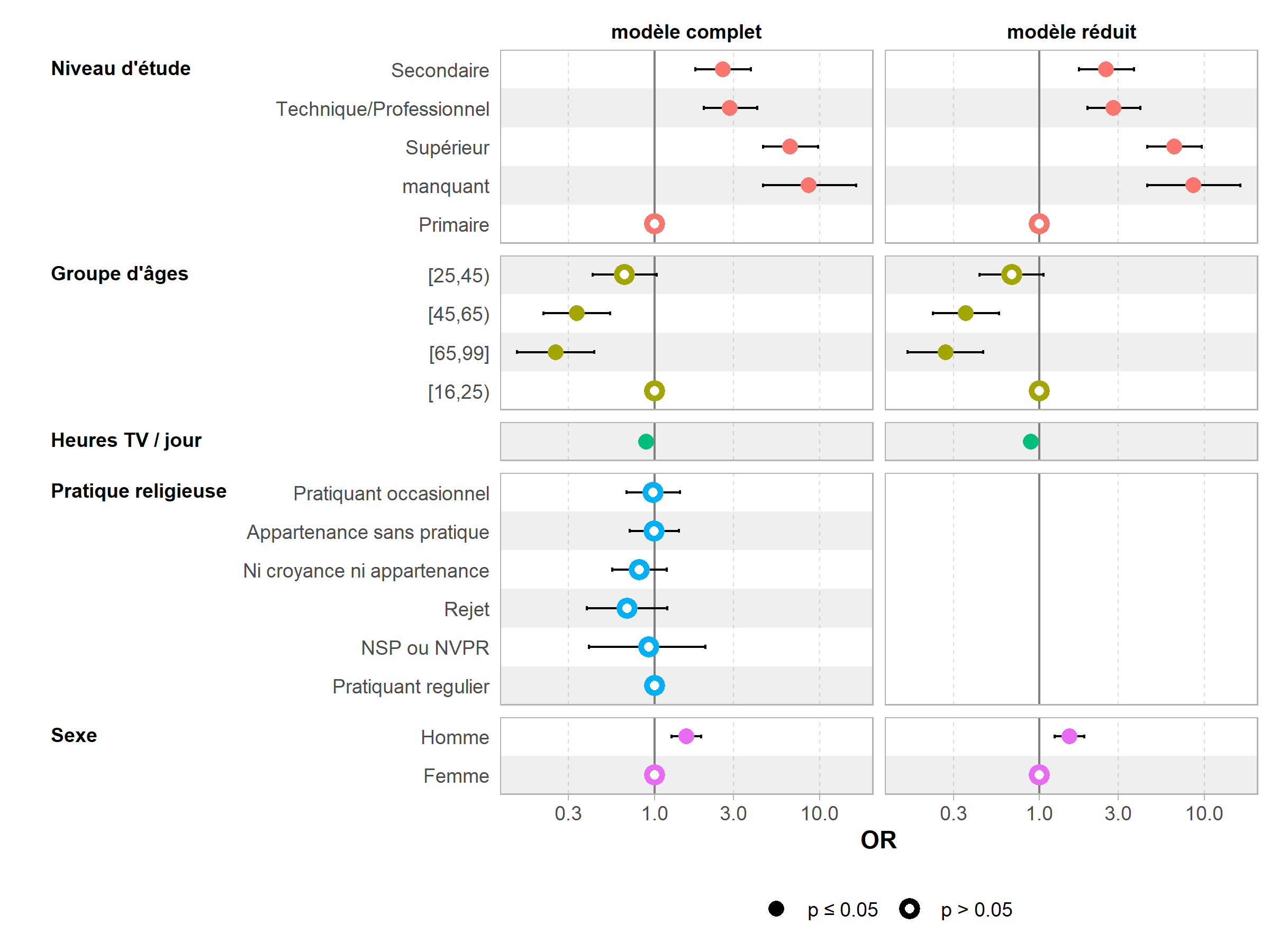
ggcoef_compare(
list("modèle complet" = reg, "modèle réduit" = reg2),
type = "faceted",
exponentiate = TRUE,
variable_labels = c(heures.tv = "Heures TV / jour")
)
Tableaux all-in-one
gtsummary
Nous avons déjà vu précédemment la fonction tbl_regression de l’extension gtsummary. Une vignette dédiée de l’extension explicite les possibilités de personnalisation des résultats. Par exemple add_global_p permet d’ajouter des p-valeurs globales pour chaque variable.
Setting theme `language: fr`| Caractéristique | OR1 | 95% IC1 | p-valeur |
|---|---|---|---|
| Sexe | <0,001 | ||
| Femme | — | — | |
| Homme | 1,55 | 1,26 – 1,91 | <0,001 |
| Groupe d'âges | <0,001 | ||
| [16,25) | — | — | |
| [25,45) | 0,66 | 0,42 – 1,03 | 0,065 |
| [45,65) | 0,34 | 0,21 – 0,54 | <0,001 |
| [65,99] | 0,25 | 0,15 – 0,43 | <0,001 |
| Niveau d'étude | <0,001 | ||
| Primaire | — | — | |
| Secondaire | 2,59 | 1,77 – 3,83 | <0,001 |
| Technique/Professionnel | 2,86 | 1,98 – 4,17 | <0,001 |
| Supérieur | 6,63 | 4,55 – 9,80 | <0,001 |
| manquant | 8,59 | 4,53 – 16,6 | <0,001 |
| Pratique religieuse | 0,5 | ||
| Pratiquant regulier | — | — | |
| Pratiquant occasionnel | 0,98 | 0,68 – 1,42 | >0,9 |
| Appartenance sans pratique | 0,99 | 0,71 – 1,40 | >0,9 |
| Ni croyance ni appartenance | 0,81 | 0,55 – 1,18 | 0,3 |
| Rejet | 0,68 | 0,39 – 1,19 | 0,2 |
| NSP ou NVPR | 0,92 | 0,40 – 2,02 | 0,8 |
| Heures de télévision / jour | 0,89 | 0,83 – 0,95 | <0,001 |
| 1 OR = rapport de cotes, IC = intervalle de confiance | |||
On peut remarquer que gtsummary (comme d’autres extensions présentées précédemment) a tenu compte des étiquettes de variables définies plus haut avec var_label de l’extension labelled (voir le chapitre sur les vecteurs labellisés).
Comme tbl_regression repose sur les extensions broom et broom.helpers, gtsummary peut en principe couvrir un plus grand nombre de modèles que finalfit (voir ci-dessous) ainsi qu’un plus grand nombre de cas particuliers (effets d’interactions, contrastes autres que traitement, paramètre polynomiaux définis avec poly.
Par défaut, les valeurs de p sont arrondies avec un nombre variable de décimales (pour ne garder que des valeurs signifiantes). Cela peut être personnalisé via l’argument pvalue_fun.
| Caractéristique | OR1 | 95% IC1 | p-valeur |
|---|---|---|---|
| Sexe | |||
| Femme | — | — | |
| Homme | 1,55 | 1,26 – 1,91 | <0,001 |
| Groupe d'âges | |||
| [16,25) | — | — | |
| [25,45) | 0,66 | 0,42 – 1,03 | 0,065 |
| [45,65) | 0,34 | 0,21 – 0,54 | <0,001 |
| [65,99] | 0,25 | 0,15 – 0,43 | <0,001 |
| Niveau d'étude | |||
| Primaire | — | — | |
| Secondaire | 2,59 | 1,77 – 3,83 | <0,001 |
| Technique/Professionnel | 2,86 | 1,98 – 4,17 | <0,001 |
| Supérieur | 6,63 | 4,55 – 9,80 | <0,001 |
| manquant | 8,59 | 4,53 – 16,6 | <0,001 |
| Pratique religieuse | |||
| Pratiquant regulier | — | — | |
| Pratiquant occasionnel | 0,98 | 0,68 – 1,42 | 0,908 |
| Appartenance sans pratique | 0,99 | 0,71 – 1,40 | 0,969 |
| Ni croyance ni appartenance | 0,81 | 0,55 – 1,18 | 0,265 |
| Rejet | 0,68 | 0,39 – 1,19 | 0,180 |
| NSP ou NVPR | 0,92 | 0,40 – 2,02 | 0,838 |
| Heures de télévision / jour | 0,89 | 0,83 – 0,95 | <0,001 |
| 1 OR = rapport de cotes, IC = intervalle de confiance | |||
tbl_merge permet de fusionner ensemble les résultats de plusieurs modèles.
tbl_merge(
tbls = list(tbl_regression(reg), tbl_regression(reg2)),
tab_spanner = c("Modèle complet", "Modèle réduit")
)| Caractéristique | Modèle complet | Modèle réduit | ||||
|---|---|---|---|---|---|---|
| log(OR)1 | 95% IC1 | p-valeur | log(OR)1 | 95% IC1 | p-valeur | |
| Sexe | ||||||
| Femme | — | — | — | — | ||
| Homme | 0,44 | 0,23 – 0,65 | <0,001 | 0,42 | 0,21 – 0,62 | <0,001 |
| Groupe d'âges | ||||||
| [16,25) | — | — | — | — | ||
| [25,45) | -0,42 | -0,87 – 0,03 | 0,065 | -0,39 | -0,84 – 0,05 | 0,084 |
| [45,65) | -1,1 | -1,6 – -0,62 | <0,001 | -1,0 | -1,5 – -0,57 | <0,001 |
| [65,99] | -1,4 | -1,9 – -0,85 | <0,001 | -1,3 | -1,8 – -0,78 | <0,001 |
| Niveau d'étude | ||||||
| Primaire | — | — | — | — | ||
| Secondaire | 0,95 | 0,57 – 1,3 | <0,001 | 0,93 | 0,55 – 1,3 | <0,001 |
| Technique/Professionnel | 1,0 | 0,68 – 1,4 | <0,001 | 1,0 | 0,67 – 1,4 | <0,001 |
| Supérieur | 1,9 | 1,5 – 2,3 | <0,001 | 1,9 | 1,5 – 2,3 | <0,001 |
| manquant | 2,2 | 1,5 – 2,8 | <0,001 | 2,1 | 1,5 – 2,8 | <0,001 |
| Pratique religieuse | ||||||
| Pratiquant regulier | — | — | ||||
| Pratiquant occasionnel | -0,02 | -0,39 – 0,35 | >0,9 | |||
| Appartenance sans pratique | -0,01 | -0,35 – 0,34 | >0,9 | |||
| Ni croyance ni appartenance | -0,22 | -0,59 – 0,16 | 0,3 | |||
| Rejet | -0,38 | -0,95 – 0,17 | 0,2 | |||
| NSP ou NVPR | -0,08 | -0,92 – 0,70 | 0,8 | |||
| Heures de télévision / jour | -0,12 | -0,19 – -0,06 | <0,001 | -0,12 | -0,19 – -0,06 | <0,001 |
| 1 OR = rapport de cotes, IC = intervalle de confiance | ||||||
L’extension gtsummary fournit également la fonction tbl_summary pour effectuer des tris à plats et/ou un tri croisé.
| Caractéristique | N = 2 0001 |
|---|---|
| Pratique du sport ? | |
| Non | 1 277 (64%) |
| Oui | 723 (36%) |
| Sexe | |
| Femme | 1 101 (55%) |
| Homme | 899 (45%) |
| Groupe d'âges | |
| [16,25) | 169 (8,5%) |
| [25,45) | 706 (35%) |
| [45,65) | 745 (37%) |
| [65,99] | 380 (19%) |
| Niveau d'étude | |
| Primaire | 466 (23%) |
| Secondaire | 387 (19%) |
| Technique/Professionnel | 594 (30%) |
| Supérieur | 441 (22%) |
| manquant | 112 (5,6%) |
| Pratique religieuse | |
| Pratiquant regulier | 266 (13%) |
| Pratiquant occasionnel | 442 (22%) |
| Appartenance sans pratique | 760 (38%) |
| Ni croyance ni appartenance | 399 (20%) |
| Rejet | 93 (4,7%) |
| NSP ou NVPR | 40 (2,0%) |
| Heures de télévision / jour | 2,00 (1,00 – 3,00) |
| Manquant | 5 |
| 1 n (%); Médiane (EI) | |
d %>%
dplyr::select(sport, sexe, grpage, etud, relig, heures.tv) %>%
tbl_summary(by = "sport", percent = "row") %>%
add_overall(last = TRUE) %>%
add_p()| Caractéristique | Non, N = 1 2771 | Oui, N = 7231 | Total, N = 2 0001 | p-valeur2 |
|---|---|---|---|---|
| Sexe | <0,001 | |||
| Femme | 747 (68%) | 354 (32%) | 1 101 (100%) | |
| Homme | 530 (59%) | 369 (41%) | 899 (100%) | |
| Groupe d'âges | <0,001 | |||
| [16,25) | 58 (34%) | 111 (66%) | 169 (100%) | |
| [25,45) | 359 (51%) | 347 (49%) | 706 (100%) | |
| [45,65) | 541 (73%) | 204 (27%) | 745 (100%) | |
| [65,99] | 319 (84%) | 61 (16%) | 380 (100%) | |
| Niveau d'étude | <0,001 | |||
| Primaire | 416 (89%) | 50 (11%) | 466 (100%) | |
| Secondaire | 270 (70%) | 117 (30%) | 387 (100%) | |
| Technique/Professionnel | 378 (64%) | 216 (36%) | 594 (100%) | |
| Supérieur | 186 (42%) | 255 (58%) | 441 (100%) | |
| manquant | 27 (24%) | 85 (76%) | 112 (100%) | |
| Pratique religieuse | 0,14 | |||
| Pratiquant regulier | 182 (68%) | 84 (32%) | 266 (100%) | |
| Pratiquant occasionnel | 295 (67%) | 147 (33%) | 442 (100%) | |
| Appartenance sans pratique | 473 (62%) | 287 (38%) | 760 (100%) | |
| Ni croyance ni appartenance | 239 (60%) | 160 (40%) | 399 (100%) | |
| Rejet | 60 (65%) | 33 (35%) | 93 (100%) | |
| NSP ou NVPR | 28 (70%) | 12 (30%) | 40 (100%) | |
| Heures de télévision / jour | 2,00 (1,00 – 3,00) | 2,00 (1,00 – 3,00) | 2,00 (1,00 – 3,00) | <0,001 |
| Manquant | 2 | 3 | 5 | |
| 1 n (%); Médiane (EI) | ||||
| 2 test du khi-deux d'indépendance; test de Wilcoxon-Mann-Whitney | ||||
Il est à noter que tbl_regression sait prendre en compte les effets d’interactions (voir ci-après).
La fonction tbl_uvregression permets quant à elle de réaliser plusieurs régressions univariées et de les présenter dans un tableau unique.
tbl_u <- d %>%
dplyr::select(sport, sexe, grpage, etud, relig, heures.tv) %>%
tbl_uvregression(
method = glm,
y = sport,
method.args = list(family = binomial),
exponentiate = TRUE,
pvalue_fun = ~ style_pvalue(.x, digits = 2)
) %>%
add_global_p() %>%
add_nevent()
tbl_u| Caractéristique | N | Event N | OR1 | 95% IC1 | p-valeur |
|---|---|---|---|---|---|
| Sexe | 2 000 | 723 | <0,001 | ||
| Femme | — | — | |||
| Homme | 1,47 | 1,22 – 1,77 | |||
| Groupe d'âges | 2 000 | 723 | <0,001 | ||
| [16,25) | — | — | |||
| [25,45) | 0,51 | 0,35 – 0,71 | |||
| [45,65) | 0,20 | 0,14 – 0,28 | |||
| [65,99] | 0,10 | 0,07 – 0,15 | |||
| Niveau d'étude | 2 000 | 723 | <0,001 | ||
| Primaire | — | — | |||
| Secondaire | 3,61 | 2,52 – 5,23 | |||
| Technique/Professionnel | 4,75 | 3,42 – 6,72 | |||
| Supérieur | 11,4 | 8,11 – 16,3 | |||
| manquant | 26,2 | 15,7 – 44,9 | |||
| Pratique religieuse | 2 000 | 723 | 0,14 | ||
| Pratiquant regulier | — | — | |||
| Pratiquant occasionnel | 1,08 | 0,78 – 1,50 | |||
| Appartenance sans pratique | 1,31 | 0,98 – 1,78 | |||
| Ni croyance ni appartenance | 1,45 | 1,05 – 2,02 | |||
| Rejet | 1,19 | 0,72 – 1,95 | |||
| NSP ou NVPR | 0,93 | 0,44 – 1,88 | |||
| Heures de télévision / jour | 1 995 | 720 | 0,79 | 0,74 – 0,84 | <0,001 |
| 1 OR = rapport de cotes, IC = intervalle de confiance | |||||
Il est possible de réunir analyse univariée et multivariée en un seul table avec tbl_merge.
tbl_m <- reg %>%
tbl_regression(
exponentiate = TRUE,
pvalue_fun = ~ style_pvalue(.x, digits = 2)
) %>%
add_global_p()
tbl_merge(
list(tbl_u, tbl_m),
tab_spanner = c("**Univarié**", "**Multivarié**")
)| Caractéristique | Univarié | Multivarié | ||||||
|---|---|---|---|---|---|---|---|---|
| N | Event N | OR1 | 95% IC1 | p-valeur | OR1 | 95% IC1 | p-valeur | |
| Sexe | 2 000 | 723 | <0,001 | <0,001 | ||||
| Femme | — | — | — | — | ||||
| Homme | 1,47 | 1,22 – 1,77 | 1,55 | 1,26 – 1,91 | ||||
| Groupe d'âges | 2 000 | 723 | <0,001 | <0,001 | ||||
| [16,25) | — | — | — | — | ||||
| [25,45) | 0,51 | 0,35 – 0,71 | 0,66 | 0,42 – 1,03 | ||||
| [45,65) | 0,20 | 0,14 – 0,28 | 0,34 | 0,21 – 0,54 | ||||
| [65,99] | 0,10 | 0,07 – 0,15 | 0,25 | 0,15 – 0,43 | ||||
| Niveau d'étude | 2 000 | 723 | <0,001 | <0,001 | ||||
| Primaire | — | — | — | — | ||||
| Secondaire | 3,61 | 2,52 – 5,23 | 2,59 | 1,77 – 3,83 | ||||
| Technique/Professionnel | 4,75 | 3,42 – 6,72 | 2,86 | 1,98 – 4,17 | ||||
| Supérieur | 11,4 | 8,11 – 16,3 | 6,63 | 4,55 – 9,80 | ||||
| manquant | 26,2 | 15,7 – 44,9 | 8,59 | 4,53 – 16,6 | ||||
| Pratique religieuse | 2 000 | 723 | 0,14 | 0,52 | ||||
| Pratiquant regulier | — | — | — | — | ||||
| Pratiquant occasionnel | 1,08 | 0,78 – 1,50 | 0,98 | 0,68 – 1,42 | ||||
| Appartenance sans pratique | 1,31 | 0,98 – 1,78 | 0,99 | 0,71 – 1,40 | ||||
| Ni croyance ni appartenance | 1,45 | 1,05 – 2,02 | 0,81 | 0,55 – 1,18 | ||||
| Rejet | 1,19 | 0,72 – 1,95 | 0,68 | 0,39 – 1,19 | ||||
| NSP ou NVPR | 0,93 | 0,44 – 1,88 | 0,92 | 0,40 – 2,02 | ||||
| Heures de télévision / jour | 1 995 | 720 | 0,79 | 0,74 – 0,84 | <0,001 | 0,89 | 0,83 – 0,95 | <0,001 |
| 1 OR = rapport de cotes, IC = intervalle de confiance | ||||||||
finalfit
L’extension finalfit fournit une fonction finalfit du type all-in-one
qui calcule un tableau avec les tris croisés, les odds ratios univariés et un modèle multivarié.
Il faut d’abord définir la variable dépendante et les variables explicatives.
Une première fonction summary_factorlist fournit un tableau descriptif avec, si l’option p = TRUE est indiquée, des tests de comparaisons (ici des tests du Chi²).
Attachement du package : 'finalfit'L'objet suivant est masqué depuis 'package:labelled':
remove_labelsOn peut remarquer que finalfit a tenu compte des étiquettes de variables définies plus haut avec var_label de l’extension labelled (voir le chapitre sur les vecteurs labellisés).
On peut associer le résultat avec la fonction kable de knitr pour un rendu plus esthétique lorsque l’on produit un rapport Rmarkdown (voir le chapitre dédié aux rapports automatisés).
| Dependent: Pratique du sport ? | Non | Oui | p | |
|---|---|---|---|---|
| Sexe | Femme | 747 (58.5) | 354 (49.0) | <0.001 |
| Homme | 530 (41.5) | 369 (51.0) | ||
| Groupe d’âges | [16,25) | 58 (4.5) | 111 (15.4) | <0.001 |
| [25,45) | 359 (28.1) | 347 (48.0) | ||
| [45,65) | 541 (42.4) | 204 (28.2) | ||
| [65,99] | 319 (25.0) | 61 (8.4) | ||
| Niveau d’étude | Primaire | 416 (32.6) | 50 (6.9) | <0.001 |
| Secondaire | 270 (21.1) | 117 (16.2) | ||
| Technique/Professionnel | 378 (29.6) | 216 (29.9) | ||
| Supérieur | 186 (14.6) | 255 (35.3) | ||
| manquant | 27 (2.1) | 85 (11.8) | ||
| Pratique religieuse | Pratiquant regulier | 182 (14.3) | 84 (11.6) | 0.144 |
| Pratiquant occasionnel | 295 (23.1) | 147 (20.3) | ||
| Appartenance sans pratique | 473 (37.0) | 287 (39.7) | ||
| Ni croyance ni appartenance | 239 (18.7) | 160 (22.1) | ||
| Rejet | 60 (4.7) | 33 (4.6) | ||
| NSP ou NVPR | 28 (2.2) | 12 (1.7) | ||
| Heures de télévision / jour | Mean (SD) | 2.5 (1.9) | 1.8 (1.4) | <0.001 |
La fonction finalfit, quant à elle, calcule à la fois les odds ratios univariés (modèles logistiques avec une seule variable inclue à la fois) et un modèle complet, présentant le tout dans un tableau synthétique.
| Dependent: Pratique du sport ? | Non | Oui | OR (univariable) | OR (multivariable) | |
|---|---|---|---|---|---|
| Sexe | Femme | 747 (67.8) | 354 (32.2) | - | - |
| Homme | 530 (59.0) | 369 (41.0) | 1.47 (1.22-1.77, p<0.001) | 1.55 (1.26-1.91, p<0.001) | |
| Groupe d’âges | [16,25) | 58 (34.3) | 111 (65.7) | - | - |
| [25,45) | 359 (50.8) | 347 (49.2) | 0.51 (0.35-0.71, p<0.001) | 0.66 (0.42-1.03, p=0.065) | |
| [45,65) | 541 (72.6) | 204 (27.4) | 0.20 (0.14-0.28, p<0.001) | 0.34 (0.21-0.54, p<0.001) | |
| [65,99] | 319 (83.9) | 61 (16.1) | - | - | |
| Niveau d’étude | Primaire | 416 (89.3) | 50 (10.7) | - | - |
| Secondaire | 270 (69.8) | 117 (30.2) | 3.61 (2.52-5.23, p<0.001) | 2.59 (1.77-3.83, p<0.001) | |
| Technique/Professionnel | 378 (63.6) | 216 (36.4) | 4.75 (3.42-6.72, p<0.001) | 2.86 (1.98-4.17, p<0.001) | |
| Supérieur | 186 (42.2) | 255 (57.8) | 11.41 (8.11-16.31, p<0.001) | 6.63 (4.55-9.80, p<0.001) | |
| manquant | 27 (24.1) | 85 (75.9) | 26.19 (15.74-44.90, p<0.001) | 8.59 (4.53-16.59, p<0.001) | |
| Pratique religieuse | Pratiquant regulier | 182 (68.4) | 84 (31.6) | - | - |
| Pratiquant occasionnel | 295 (66.7) | 147 (33.3) | 1.08 (0.78-1.50, p=0.644) | 0.98 (0.68-1.42, p=0.908) | |
| Appartenance sans pratique | 473 (62.2) | 287 (37.8) | 1.31 (0.98-1.78, p=0.071) | 0.99 (0.71-1.40, p=0.969) | |
| Ni croyance ni appartenance | 239 (59.9) | 160 (40.1) | 1.45 (1.05-2.02, p=0.026) | 0.81 (0.55-1.18, p=0.265) | |
| Rejet | 60 (64.5) | 33 (35.5) | 1.19 (0.72-1.95, p=0.489) | 0.68 (0.39-1.19, p=0.180) | |
| NSP ou NVPR | 28 (70.0) | 12 (30.0) | 0.93 (0.44-1.88, p=0.841) | 0.92 (0.40-2.02, p=0.838) | |
| Heures de télévision / jour | Mean (SD) | 2.5 (1.9) | 1.8 (1.4) | 0.79 (0.74-0.84, p<0.001) | 0.89 (0.83-0.95, p<0.001) |
| NA | NA | NA | NA | 0.10 (0.07-0.15, p<0.001) | 0.25 (0.15-0.43, p<0.001) |
Par défaut, toutes les variables explicatives fournies sont retenues dans le modèle affiché. Si on ne souhaite inclure que certaines variables dans le modèle mutivarié (parce que l’on aura précédemment réalisé une procédure step), il faudra préciser séparément les variables du modèle multivarié.
vars_multi <- c("sexe", "grpage", "etud", "heures.tv")
tab <- finalfit(d, dep, vars, explanatory_multi = vars_multi)
knitr::kable(tab, row.names = FALSE)| Dependent: Pratique du sport ? | Non | Oui | OR (univariable) | OR (multivariable) | |
|---|---|---|---|---|---|
| Sexe | Femme | 747 (67.8) | 354 (32.2) | - | - |
| Homme | 530 (59.0) | 369 (41.0) | 1.47 (1.22-1.77, p<0.001) | 1.52 (1.24-1.87, p<0.001) | |
| Groupe d’âges | [16,25) | 58 (34.3) | 111 (65.7) | - | - |
| [25,45) | 359 (50.8) | 347 (49.2) | 0.51 (0.35-0.71, p<0.001) | 0.68 (0.43-1.06, p=0.084) | |
| [45,65) | 541 (72.6) | 204 (27.4) | 0.20 (0.14-0.28, p<0.001) | 0.36 (0.23-0.57, p<0.001) | |
| [65,99] | 319 (83.9) | 61 (16.1) | - | - | |
| Niveau d’étude | Primaire | 416 (89.3) | 50 (10.7) | - | - |
| Secondaire | 270 (69.8) | 117 (30.2) | 3.61 (2.52-5.23, p<0.001) | 2.54 (1.73-3.75, p<0.001) | |
| Technique/Professionnel | 378 (63.6) | 216 (36.4) | 4.75 (3.42-6.72, p<0.001) | 2.81 (1.95-4.10, p<0.001) | |
| Supérieur | 186 (42.2) | 255 (57.8) | 11.41 (8.11-16.31, p<0.001) | 6.55 (4.50-9.66, p<0.001) | |
| manquant | 27 (24.1) | 85 (75.9) | 26.19 (15.74-44.90, p<0.001) | 8.54 (4.51-16.47, p<0.001) | |
| Pratique religieuse | Pratiquant regulier | 182 (68.4) | 84 (31.6) | - | - |
| Pratiquant occasionnel | 295 (66.7) | 147 (33.3) | 1.08 (0.78-1.50, p=0.644) | - | |
| Appartenance sans pratique | 473 (62.2) | 287 (37.8) | 1.31 (0.98-1.78, p=0.071) | - | |
| Ni croyance ni appartenance | 239 (59.9) | 160 (40.1) | 1.45 (1.05-2.02, p=0.026) | - | |
| Rejet | 60 (64.5) | 33 (35.5) | 1.19 (0.72-1.95, p=0.489) | - | |
| NSP ou NVPR | 28 (70.0) | 12 (30.0) | 0.93 (0.44-1.88, p=0.841) | - | |
| Heures de télévision / jour | Mean (SD) | 2.5 (1.9) | 1.8 (1.4) | 0.79 (0.74-0.84, p<0.001) | 0.89 (0.83-0.95, p<0.001) |
| NA | NA | NA | NA | 0.10 (0.07-0.15, p<0.001) | 0.27 (0.16-0.46, p<0.001) |
On pourra se référer à l’aide de la fonction finalfit pour d’autres exemples.
L’extension finalfit propose aussi une fonction or_plot pour présenter les odd ratios obtenus sous forme de graphique.
Attente de la réalisation du profilage...
Attente de la réalisation du profilage...
Attente de la réalisation du profilage...Warning: Removed 4 rows containing missing values
(`geom_errorbarh()`).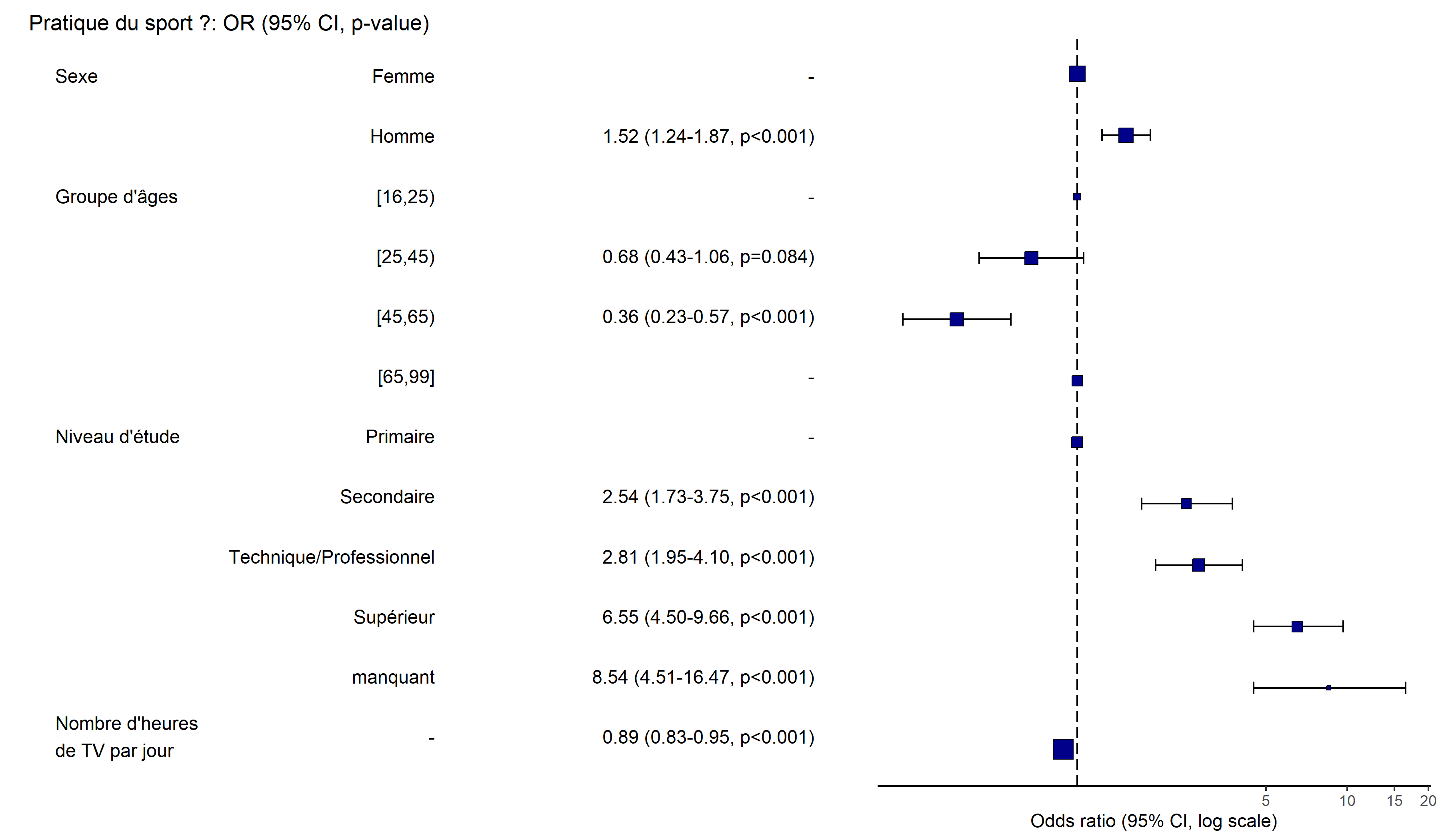
ATTENTION : or_plot n’est pas compatible avec les effets d’interactions (cf. ci-dessous).
Multicolinéarité
Voir le chapitre dédié.
Régression logistique multinomiale
La régression logistique multinomiale est évoquée dans le webin-R #17 (trajectoires de soins : un exemple de données longitudinales) sur YouTube.
La régression logistique multinomiale est une extension de la régression logistique aux variables qualitatives à trois modalités ou plus. Dans ce cas de figure, chaque modalité de la variable d’intérêt sera comparée à la modalité de réference. Les odds ratio seront donc exprimés par rapport à cette dernière.
Nous allons prendre pour exemple la variable trav.satisf, à savoir la satisfaction ou l’insatisfaction au travail.
Nous allons choisir comme modalité de référence la position intermédiaire, à savoir l’« équilibre ».
Enfin, nous allons aussi en profiter pour raccourcir les étiquettes de la variable trav.imp :
Pour calculer un modèle logistique multinomial, nous allons utiliser la fonction multinom de l’extension nnet5. La syntaxe de multinom est similaire à celle de glm, le paramètre family en moins.
# weights: 39 (24 variable)
initial value 1151.345679
iter 10 value 977.348901
iter 20 value 969.849189
iter 30 value 969.522965
final value 969.521855
convergedComme pour la régression logistique, il est possible de réaliser une sélection pas à pas descendante :
Start: AIC=1987.04
trav.satisf ~ sexe + etud + grpage + trav.imp
trying - sexe
# weights: 36 (22 variable)
initial value 1151.345679
iter 10 value 978.538886
iter 20 value 970.453555
iter 30 value 970.294459
final value 970.293988
converged
trying - etud
# weights: 27 (16 variable)
initial value 1151.345679
iter 10 value 987.907714
iter 20 value 981.785467
iter 30 value 981.762800
final value 981.762781
converged
trying - grpage
# weights: 30 (18 variable)
initial value 1151.345679
iter 10 value 979.485430
iter 20 value 973.175923
final value 973.172389
converged
trying - trav.imp
# weights: 30 (18 variable)
initial value 1151.345679
iter 10 value 998.803976
iter 20 value 994.417973
iter 30 value 994.378914
final value 994.378869
converged
Df AIC
- grpage 18 1982.345
- sexe 22 1984.588
<none> 24 1987.044
- etud 16 1995.526
- trav.imp 18 2024.758
# weights: 30 (18 variable)
initial value 1151.345679
iter 10 value 979.485430
iter 20 value 973.175923
final value 973.172389
converged
Step: AIC=1982.34
trav.satisf ~ sexe + etud + trav.imp
trying - sexe
# weights: 27 (16 variable)
initial value 1151.345679
iter 10 value 976.669670
iter 20 value 973.928385
iter 20 value 973.928377
iter 20 value 973.928377
final value 973.928377
converged
trying - etud
# weights: 18 (10 variable)
initial value 1151.345679
iter 10 value 988.413720
final value 985.085797
converged
trying - trav.imp
# weights: 21 (12 variable)
initial value 1151.345679
iter 10 value 1001.517287
final value 998.204280
converged
Df AIC
- sexe 16 1979.857
<none> 18 1982.345
- etud 10 1990.172
- trav.imp 12 2020.409
# weights: 27 (16 variable)
initial value 1151.345679
iter 10 value 976.669670
iter 20 value 973.928385
iter 20 value 973.928377
iter 20 value 973.928377
final value 973.928377
converged
Step: AIC=1979.86
trav.satisf ~ etud + trav.imp
trying - etud
# weights: 15 (8 variable)
initial value 1151.345679
iter 10 value 986.124104
final value 986.034023
converged
trying - trav.imp
# weights: 18 (10 variable)
initial value 1151.345679
iter 10 value 1000.225356
final value 998.395273
converged
Df AIC
<none> 16 1979.857
- etud 8 1988.068
- trav.imp 10 2016.791La plupart des fonctions vues précédemment fonctionnent, y compris tbl_regression (par contre, add_global_p n’est pour le moment pas compatible) :
Call:
multinom(formula = trav.satisf ~ etud + trav.imp, data = d)
Coefficients:
(Intercept) etudSecondaire
Satisfaction -0.1110996 0.04916210
Insatisfaction -1.1213760 -0.09737523
etudTechnique/Professionnel etudSupérieur
Satisfaction 0.07793241 0.69950061
Insatisfaction 0.08392603 0.07755307
etudmanquant trav.impAussi trav.impMoins
Satisfaction -0.53841577 0.2578973 -0.1756206
Insatisfaction -0.04364055 -0.2279774 -0.5330349
trav.impPeu
Satisfaction -0.5995051
Insatisfaction 1.3401509
Std. Errors:
(Intercept) etudSecondaire
Satisfaction 0.4520902 0.2635573
Insatisfaction 0.6516992 0.3999875
etudTechnique/Professionnel etudSupérieur
Satisfaction 0.2408483 0.2472571
Insatisfaction 0.3579684 0.3831110
etudmanquant trav.impAussi trav.impMoins
Satisfaction 0.5910993 0.4260623 0.4115818
Insatisfaction 0.8407592 0.6213781 0.5941721
trav.impPeu
Satisfaction 0.5580115
Insatisfaction 0.6587383
Residual Deviance: 1947.857
AIC: 1979.857 ℹ Multinomial models have a different underlying structure than the models
gtsummary was designed for. Other gtsummary functions designed to work with
tbl_regression objects may yield unexpected results.| Characteristic | OR1 | 95% CI1 | p-value |
|---|---|---|---|
| Satisfaction | |||
| Niveau d'étude | |||
| Primaire | — | — | |
| Secondaire | 1.05 | 0.63, 1.76 | 0.9 |
| Technique/Professionnel | 1.08 | 0.67, 1.73 | 0.7 |
| Supérieur | 2.01 | 1.24, 3.27 | 0.005 |
| manquant | 0.58 | 0.18, 1.86 | 0.4 |
| Importance du travail | |||
| Le plus | — | — | |
| Aussi | 1.29 | 0.56, 2.98 | 0.5 |
| Moins | 0.84 | 0.37, 1.88 | 0.7 |
| Peu | 0.55 | 0.18, 1.64 | 0.3 |
| Insatisfaction | |||
| Niveau d'étude | |||
| Primaire | — | — | |
| Secondaire | 0.91 | 0.41, 1.99 | 0.8 |
| Technique/Professionnel | 1.09 | 0.54, 2.19 | 0.8 |
| Supérieur | 1.08 | 0.51, 2.29 | 0.8 |
| manquant | 0.96 | 0.18, 4.97 | >0.9 |
| Importance du travail | |||
| Le plus | — | — | |
| Aussi | 0.80 | 0.24, 2.69 | 0.7 |
| Moins | 0.59 | 0.18, 1.88 | 0.4 |
| Peu | 3.82 | 1.05, 13.9 | 0.042 |
| 1 OR = Odds Ratio, CI = Confidence Interval | |||
De même, il est possible de calculer la matrice de confusion :
Equilibre Satisfaction Insatisfaction
Equilibre 262 211 49
Satisfaction 171 258 45
Insatisfaction 18 11 23La fonction tidy_plus_plus peut s’appliquer au résultat de multinom :
On notera la présence d’une colonne supplémentaire, y.level. De fait, la fonction ggcoef_model de GGally ne peut s’appliquer directement, car les coefficients vont se supperposer. On aura dès lors recours à sa variante ggcoef_multinom dédiée aux modèles multinomiax.
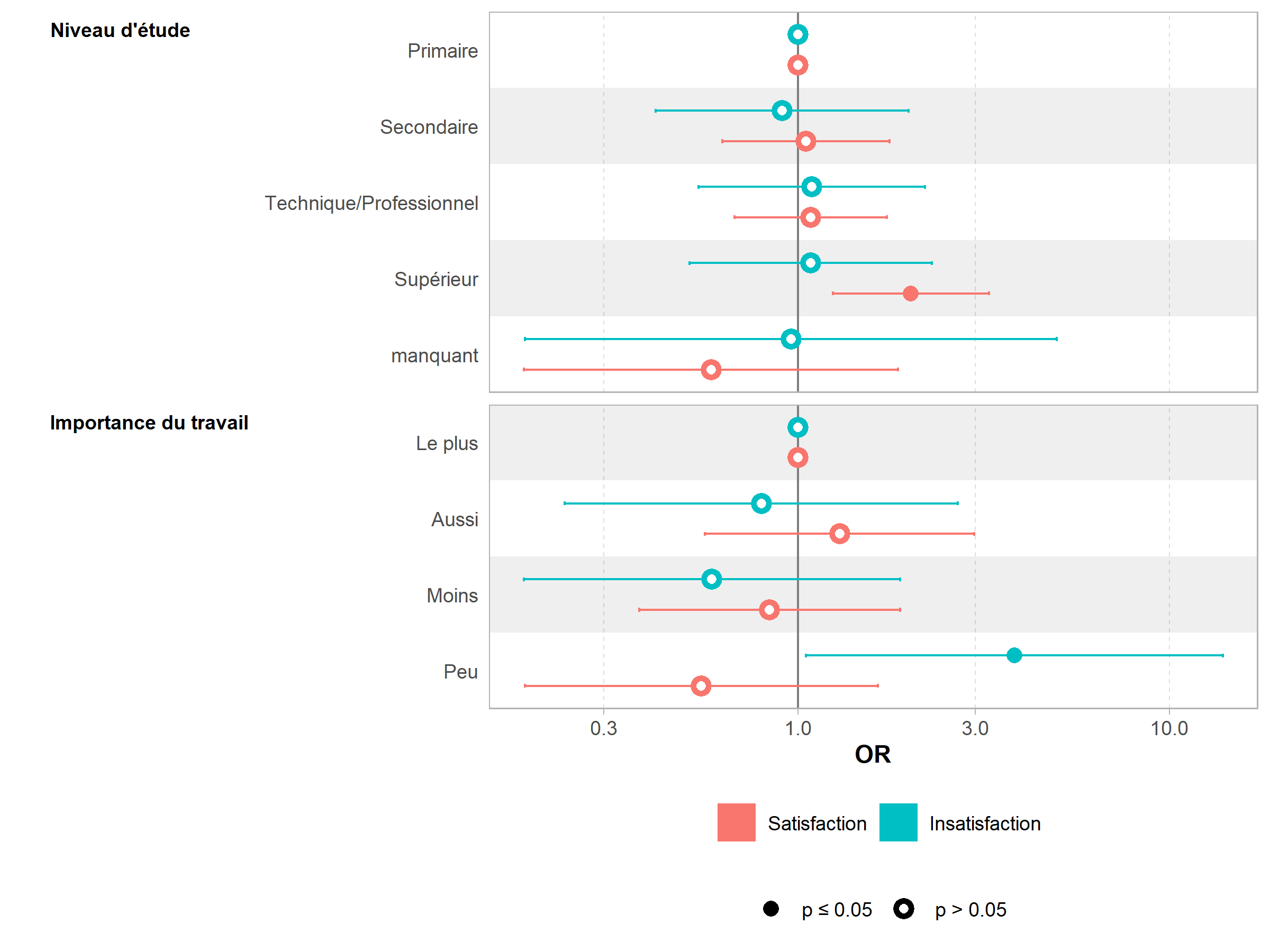
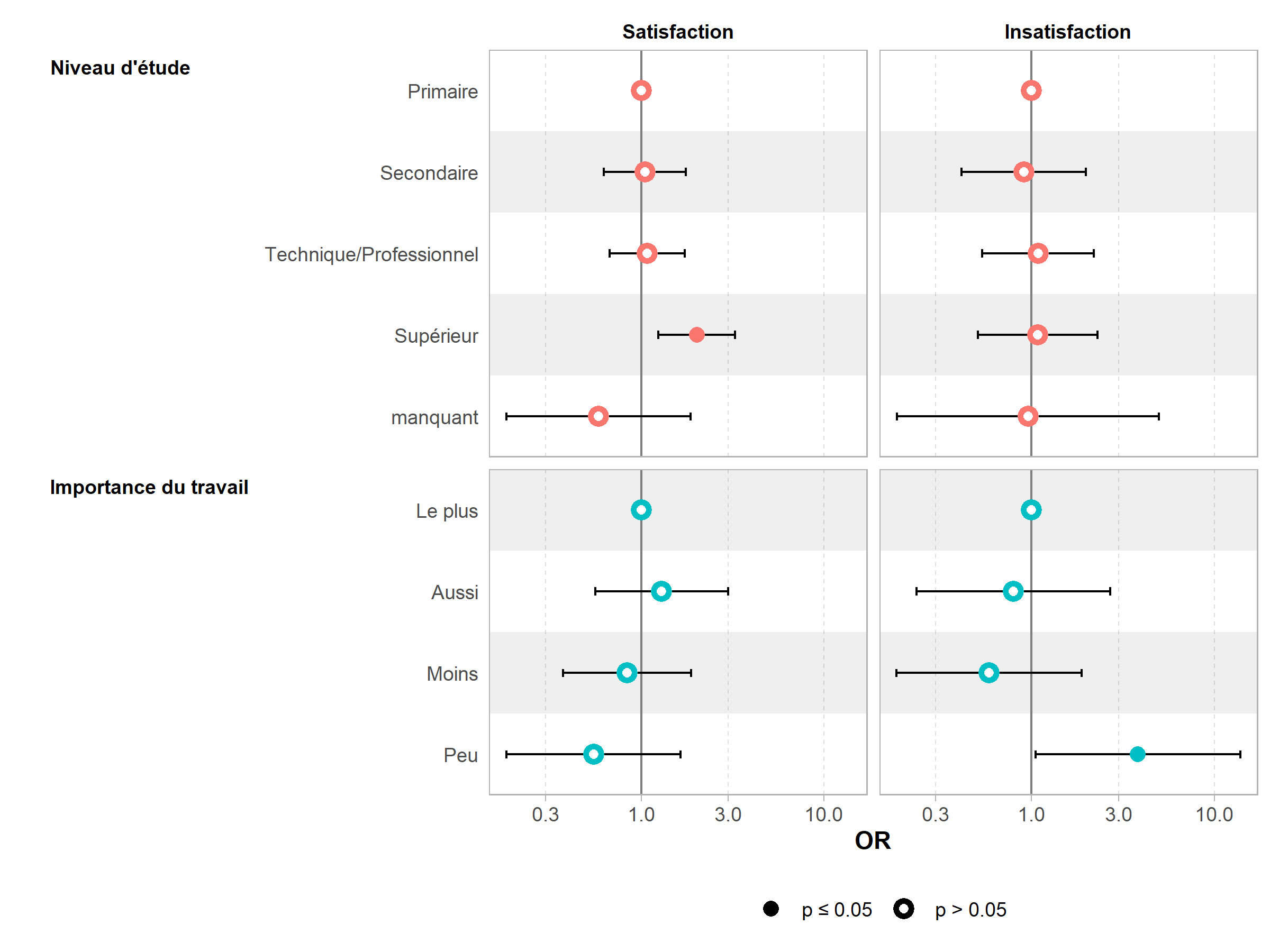
Il est possible de représenter les effets marginaux du modèle avec la fonction allEffects de l’extension effects.
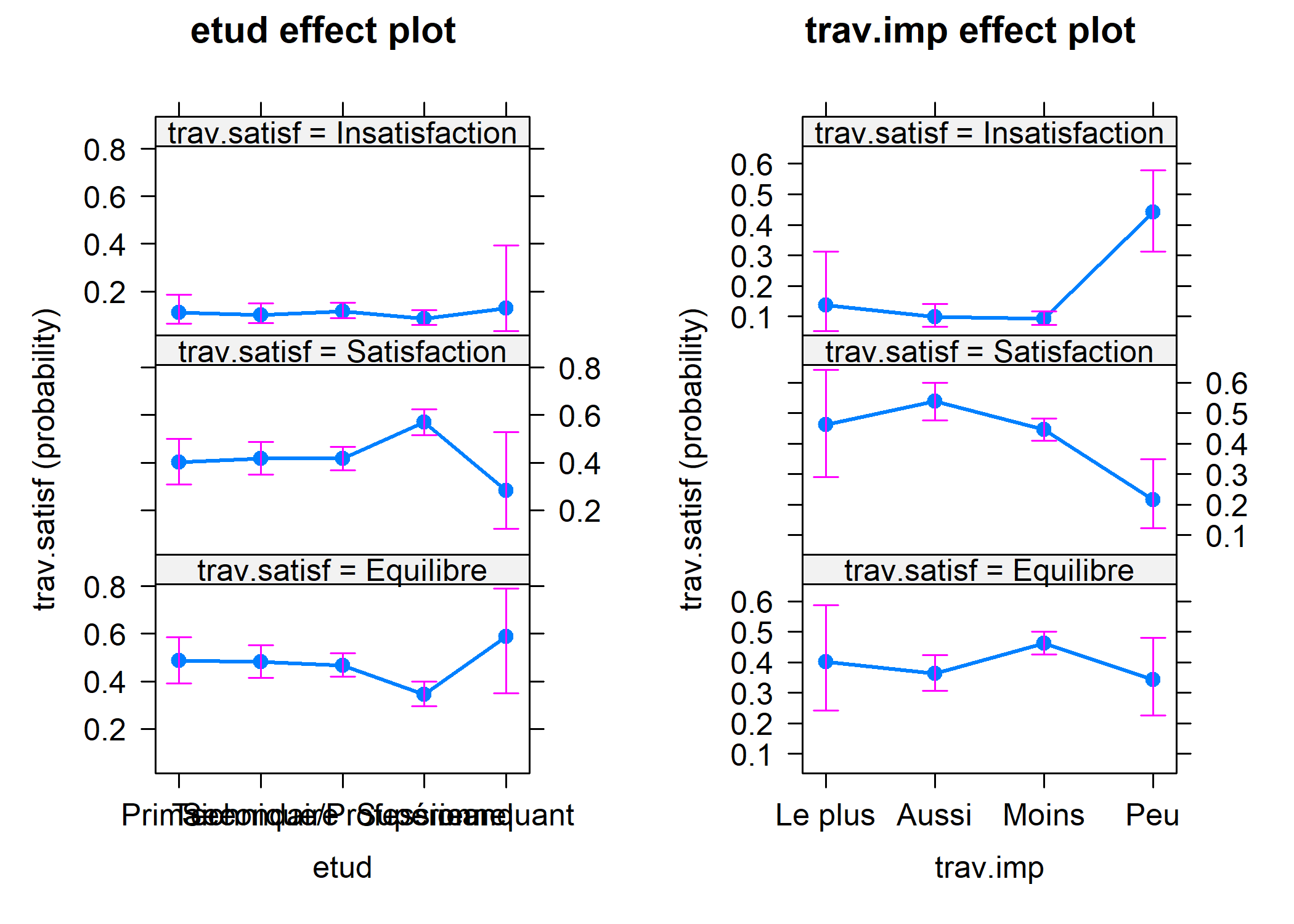
Une alternative est d’avoir recours à la fonction ggeffect de l’extension ggeffects.
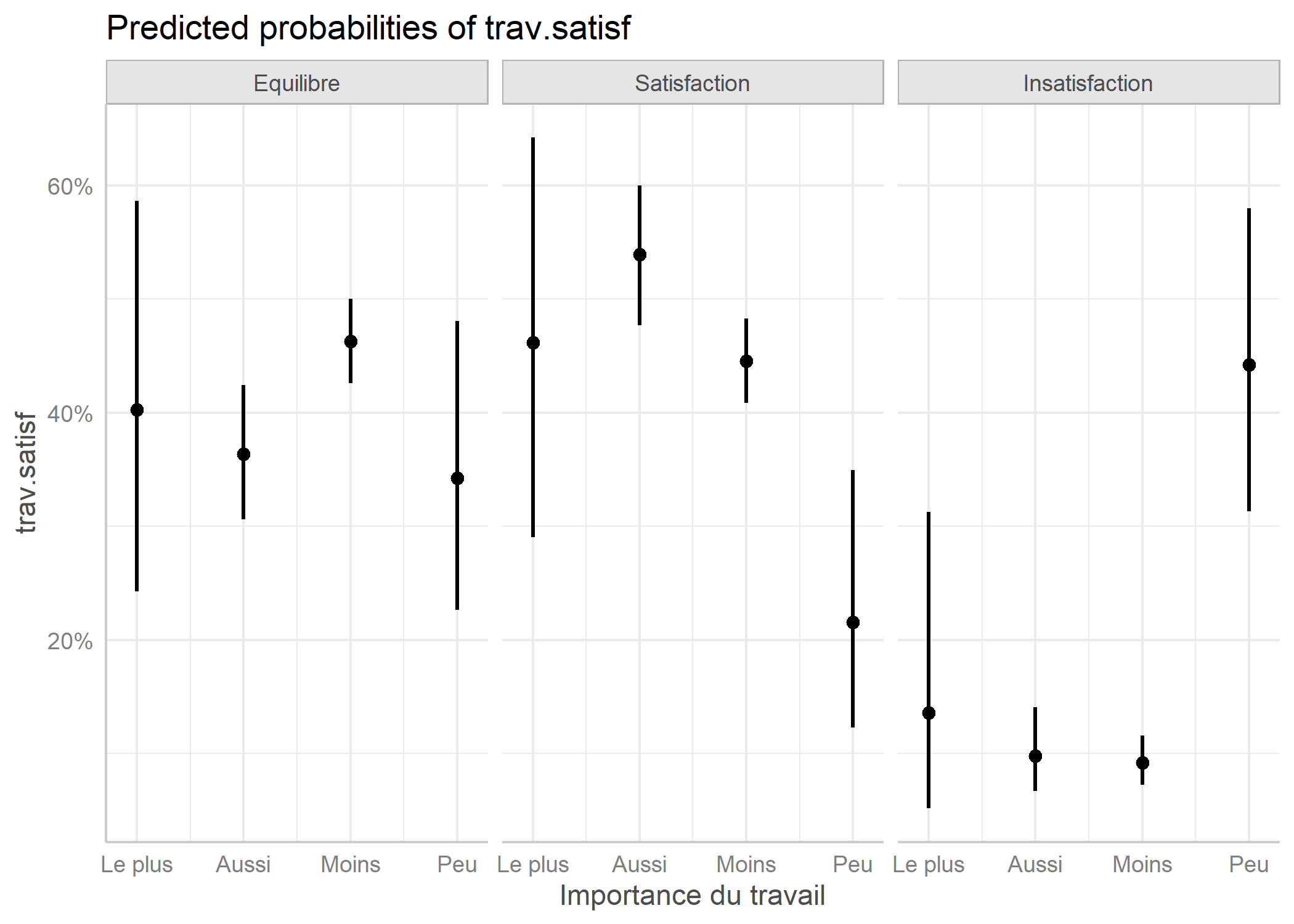
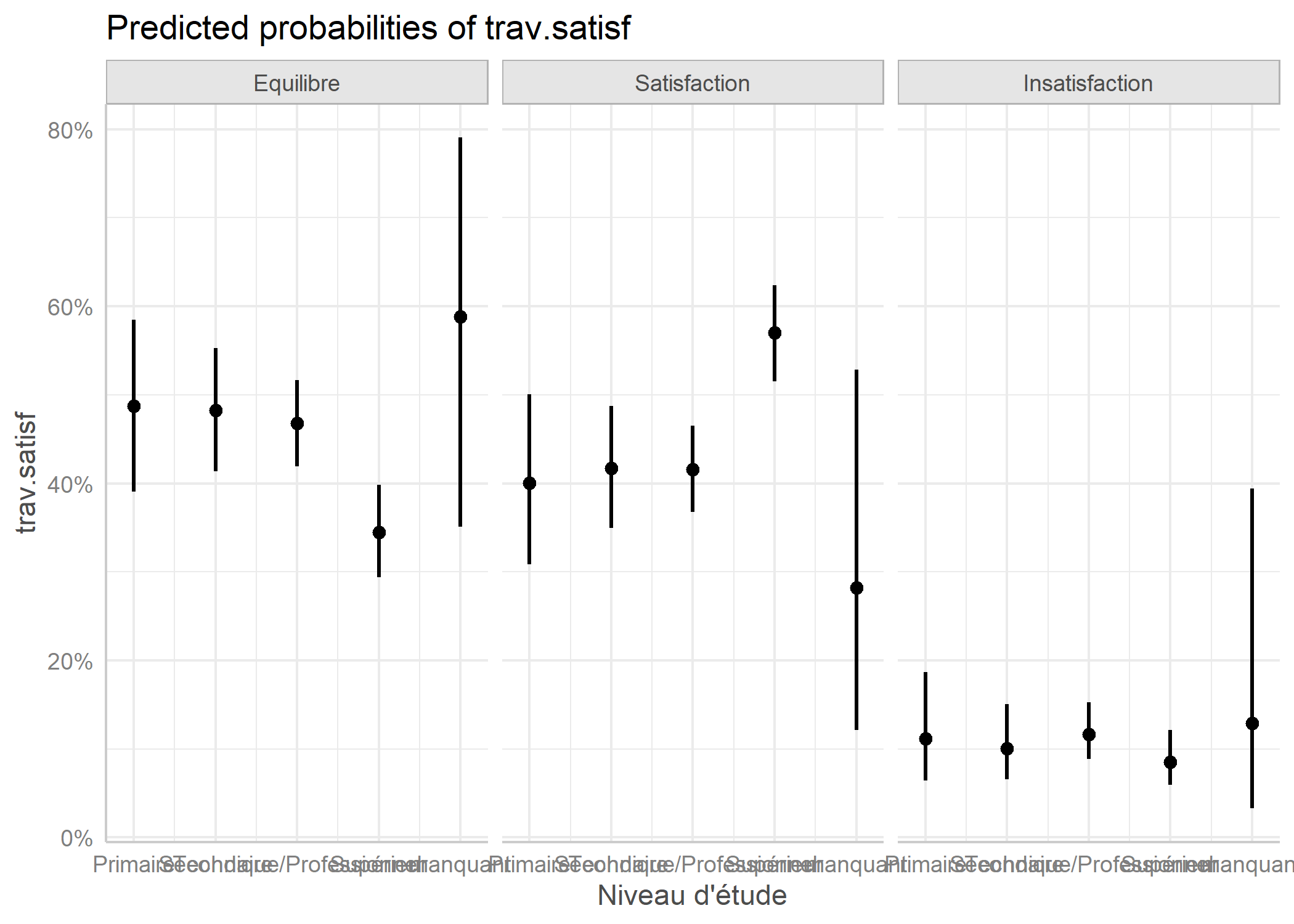
Régression logistique ordinale
La régression logistique ordinale s’applique lorsque la variable à expliquer possède trois ou plus modalités qui sont ordonnées (par exemple : modéré, moyen, fort).
L’extension la plus utilisée pour réaliser des modèles ordinaux est ordinal et sa fonction clm. Il est même possible de réaliser des modèles ordinaux avec des effets aléatoires (modèles mixtes) à l’aide de la fonction clmm.
Pour une bonne introduction à l’extension ordinal, on pourra se référer au tutoriel officiel (en anglais) : https://cran.r-project.org/web/packages/ordinal/vignettes/.
Une autre introduction pertinente (en français) et utilisant cette fois-ci l’extention VGAM et sa fonction vglm est disponible sur le site de l’université de Lyon : https://eric.univ-lyon2.fr/~ricco/cours/didacticiels/data-mining/didacticiel_Reg_Logistique_Polytomique_Ordinale.pdf.
On va reprendre l’exemple précédent puisque la variable trav.satisf est une variable ordonnée.
ATTENTION : Dans le cas d’une régression logistique ordinale, il importante que les niveaux du facteur soient classés selon leur ordre hiéarchique (du plus faible au plus fort). On va dès lors recoder notre variable à expliquer.
d$trav.satisf <- factor(d$trav.satisf, c("Insatisfaction", "Equilibre", "Satisfaction"), ordered = TRUE)
freq(d$trav.satisf)
Attachement du package : 'ordinal'L'objet suivant est masqué depuis 'package:plotly':
sliceL'objet suivant est masqué depuis 'package:breakDown':
wineL'objet suivant est masqué depuis 'package:dplyr':
sliceformula: trav.satisf ~ sexe + etud + trav.imp
data: d
link threshold nobs logLik AIC niter max.grad
logit flexible 1048 -978.61 1977.23 5(0) 5.41e-09
cond.H
3.9e+02
Coefficients:
Estimate Std. Error z value
sexeHomme -0.16141 0.12215 -1.321
etudSecondaire 0.05558 0.23220 0.239
etudTechnique/Professionnel 0.03373 0.21210 0.159
etudSupérieur 0.61336 0.21972 2.792
etudmanquant -0.45555 0.48761 -0.934
trav.impAussi 0.35104 0.38578 0.910
trav.impMoins 0.02616 0.37174 0.070
trav.impPeu -1.66062 0.46204 -3.594
Pr(>|z|)
sexeHomme 0.186369
etudSecondaire 0.810819
etudTechnique/Professionnel 0.873660
etudSupérieur 0.005245 **
etudmanquant 0.350174
trav.impAussi 0.362857
trav.impMoins 0.943896
trav.impPeu 0.000325 ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Threshold coefficients:
Estimate Std. Error z value
Insatisfaction|Equilibre -2.0226 0.4189 -4.829
Equilibre|Satisfaction 0.3391 0.4113 0.825
(952 observations effacées parce que manquantes)Une fois encore, il est possible de faire une sélection descendante pas à pas.
Start: AIC=1977.23
trav.satisf ~ sexe + etud + trav.imp
Df AIC
- sexe 1 1977.0
<none> 1977.2
- etud 4 1990.6
- trav.imp 3 2013.2
Step: AIC=1976.97
trav.satisf ~ etud + trav.imp
Df AIC
<none> 1977.0
- etud 4 1990.6
- trav.imp 3 2011.6L’extension broom propose une méthode tidy pour les objets clm.
La méthode tidy étant disponible, on peut utiliser ggcoef_model et tbl_regression.
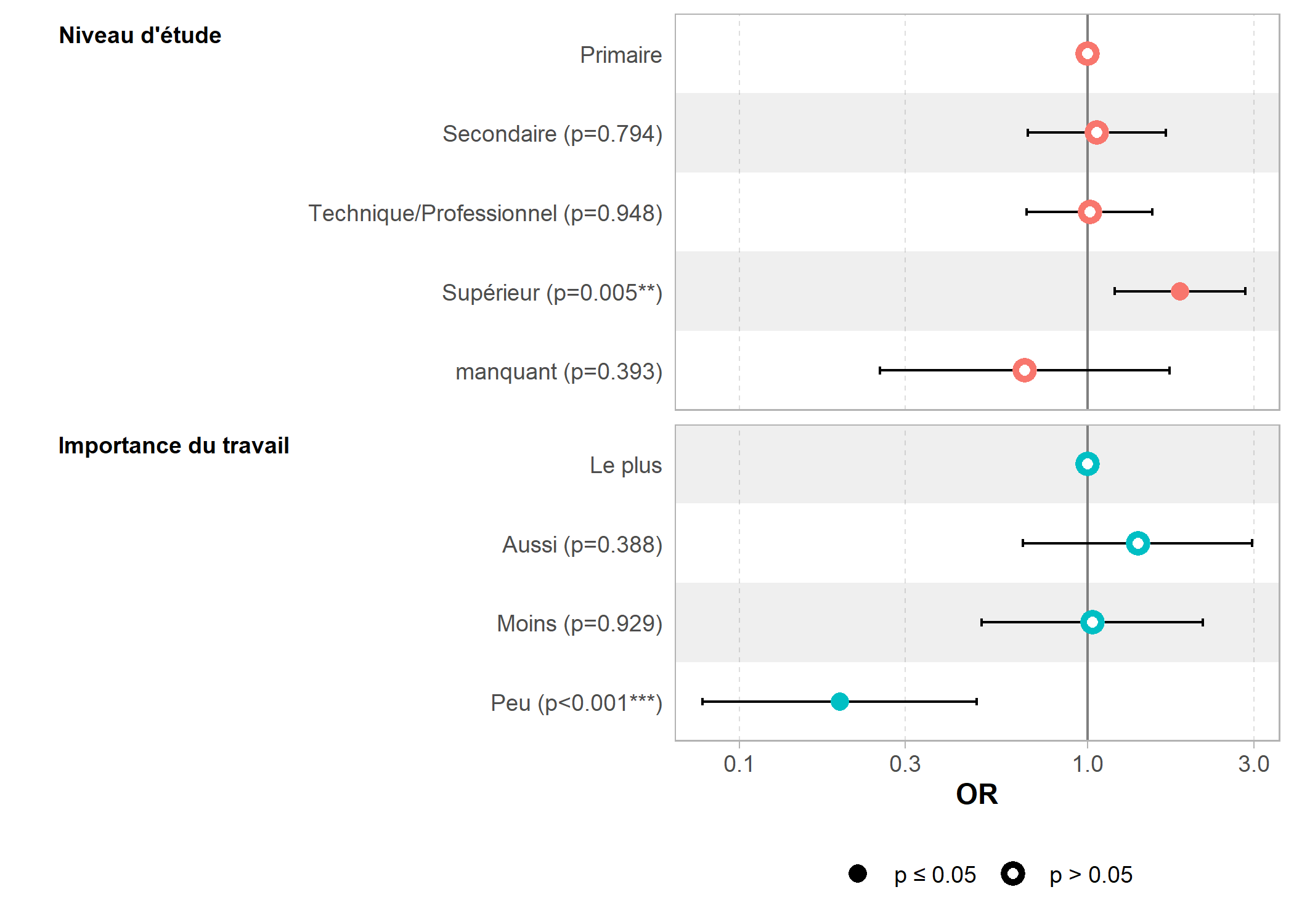
| Characteristic | OR1 | 95% CI1 | p-value |
|---|---|---|---|
| Sexe | |||
| Femme | — | — | |
| Homme | 0.85 | 0.67, 1.08 | 0.2 |
| Niveau d'étude | |||
| Primaire | — | — | |
| Secondaire | 1.06 | 0.67, 1.67 | 0.8 |
| Technique/Professionnel | 1.03 | 0.68, 1.57 | 0.9 |
| Supérieur | 1.85 | 1.20, 2.84 | 0.005 |
| manquant | 0.63 | 0.24, 1.66 | 0.4 |
| Importance du travail | |||
| Le plus | — | — | |
| Aussi | 1.42 | 0.66, 3.03 | 0.4 |
| Moins | 1.03 | 0.49, 2.13 | >0.9 |
| Peu | 0.19 | 0.08, 0.47 | <0.001 |
| 1 OR = Odds Ratio, CI = Confidence Interval | |||
Données pondérées et l’extension survey
Lorsque l’on utilise des données pondérées, on aura recours à l’extension survey6.
Préparons des données d’exemple :
Régression logistique binaire
L’extension survey fournit une fonction svyglm permettant de calculer un modèle statistique tout en prenant en compte le plan d’échantillonnage spécifié. La syntaxe de svyglm est proche de celle de glm. Cependant, le cadre d’une régression logistique, il est nécessaire d’utiliser family = quasibinomial() afin d’éviter un message d’erreur indiquant un nombre non entier de succès :
Warning in eval(family$initialize): nombre de succès non
entier dans un glm binomial !Independent Sampling design (with replacement)
svydesign(ids = ~1, data = d, weights = ~poids)
Call: svyglm(formula = sport ~ sexe + age + relig + heures.tv, design = dw,
family = quasibinomial())
Coefficients:
(Intercept)
1.53590
sexeHomme
0.36526
age
-0.04127
religPratiquant occasionnel
0.05577
religAppartenance sans pratique
0.16367
religNi croyance ni appartenance
0.03988
religRejet
-0.14862
religNSP ou NVPR
-0.22682
heures.tv
-0.18204
Degrees of Freedom: 1994 Total (i.e. Null); 1986 Residual
(5 observations effacées parce que manquantes)
Null Deviance: 2672
Residual Deviance: 2378 AIC: NALe résultat obtenu est similaire à celui de glm et l’on peut utiliser sans problème les fonctions coef, confint, odds.ratio, predict ou encore tidy, tidy_plus_plus et ggcoef_model.
| Characteristic | OR1 | 95% CI1 | p-value |
|---|---|---|---|
| Sexe | |||
| Femme | — | — | |
| Homme | 1.44 | 1.12, 1.85 | 0.004 |
| age | 0.96 | 0.95, 0.97 | <0.001 |
| Pratique religieuse | |||
| Pratiquant regulier | — | — | |
| Pratiquant occasionnel | 1.06 | 0.66, 1.70 | 0.8 |
| Appartenance sans pratique | 1.18 | 0.76, 1.83 | 0.5 |
| Ni croyance ni appartenance | 1.04 | 0.65, 1.68 | 0.9 |
| Rejet | 0.86 | 0.43, 1.74 | 0.7 |
| NSP ou NVPR | 0.80 | 0.32, 1.96 | 0.6 |
| Nombre d'heures de TV par jour | 0.83 | 0.77, 0.90 | <0.001 |
| 1 OR = Odds Ratio, CI = Confidence Interval | |||
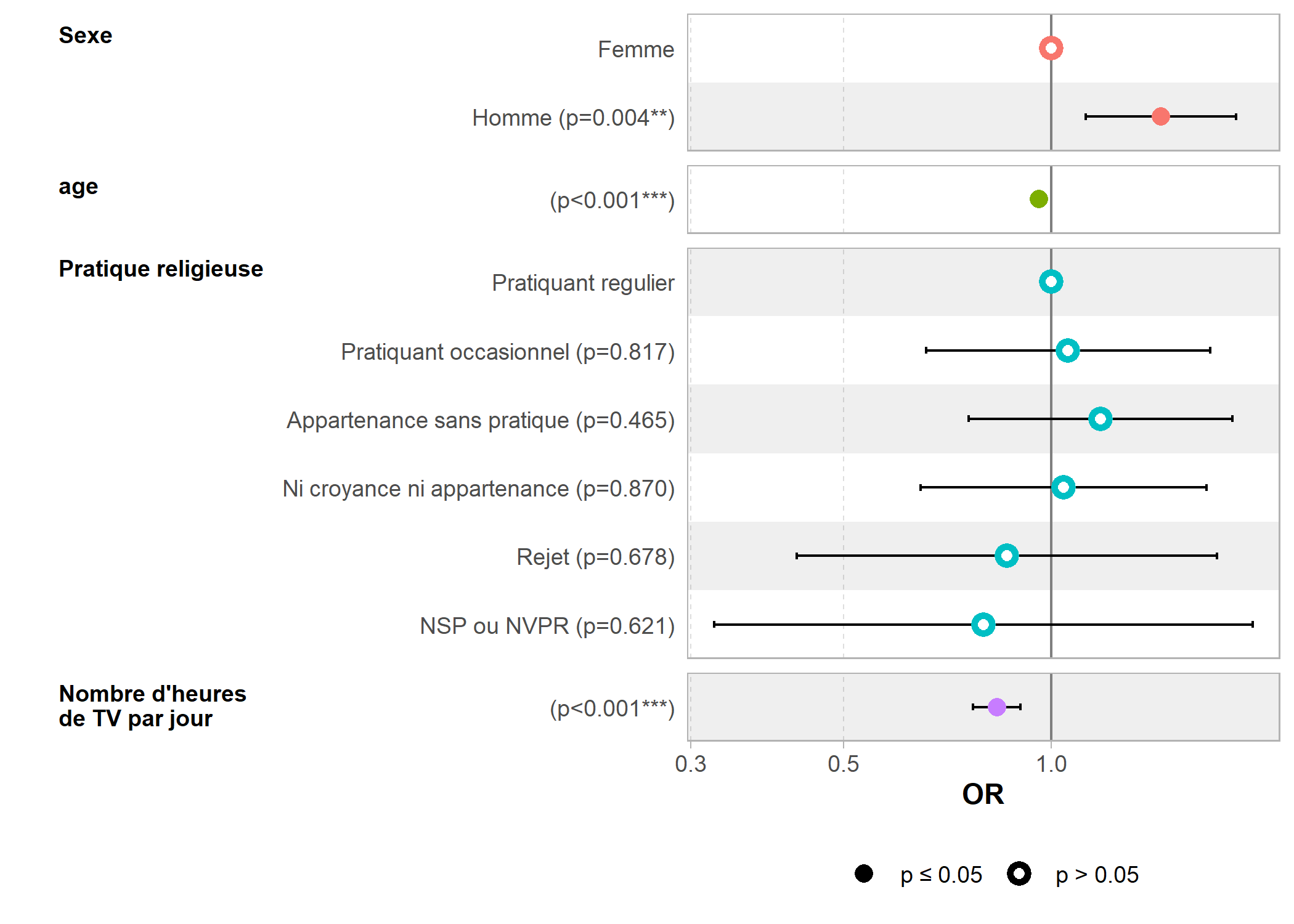
Dans ses dernières versions, survey fournit une méthode AIC.svyglm permettant d’estimer un AIC sur un modèle calculé avec svyglm. Il est dès lors possible d’utiliser la fonction step pour réaliser une sélection descendante pas à pas.
L’extension effects n’est quant à elle pas compatible avec svyglm7.
Régression multinomiale
L’extension survey ne fournit pas de fonction adaptée aux régressions multinomiales. Cependant, il est possible d’en réaliser une en ayant recours à des poids de réplication, comme suggéré par Thomas Lumley dans son ouvrage Complex Surveys: A Guide to Analysis Using R. Thomas Lumley est par ailleurs l’auteur de l’extension survey.
L’extension svrepmisc disponible sur GitHub fournit quelques fonctions facilitant l’utilisation des poids de réplication avec survey. Pour l’installer, on utilisera le code ci-dessous :
En premier lieu, il faut définir le design de notre tableau de données puis calculer des poids de réplication.
library(survey)
dw <- svydesign(ids = ~1, data = d, weights = ~poids)
dwr <- as.svrepdesign(dw, type = "bootstrap", replicates = 100)Il faut prévoir un nombre de replicates suffisant pour calculer ultérieurement les intervalles de confiance des coefficients. Plus ce nombre est élevé, plus précise sera l’estimation de la variance et donc des valeurs p et des intervalles de confiance. Cependant, plus ce nombre est élevé, plus le temps de calcul sera important.
svrepmisc fournit une fonction svymultinom pour le calcul d’une régression multinomiale avec des poids de réplication.
svrepmisc fournit également des méthodes confint et tidy. Il est également possible d’utiliser ggcoef.
Coefficient
Equilibre.(Intercept) 0.93947
Satisfaction.(Intercept) 0.74127
Equilibre.sexeHomme -0.24304
Satisfaction.sexeHomme -0.27381
Equilibre.etudSecondaire -0.41802
Satisfaction.etudSecondaire -0.26579
Equilibre.etudTechnique/Professionnel -0.47708
Satisfaction.etudTechnique/Professionnel -0.23585
Equilibre.etudSupérieur -0.57579
Satisfaction.etudSupérieur 0.36801
Equilibre.etudmanquant -0.32346
Satisfaction.etudmanquant -0.65343
Equilibre.grpage[25,45) 0.60710
Satisfaction.grpage[25,45) 0.46941
Equilibre.grpage[45,65) 0.57989
Satisfaction.grpage[45,65) 0.52873
Equilibre.grpage[65,99] -3.20673
Satisfaction.grpage[65,99] 11.60092
Equilibre.trav.impAussi 0.42551
Satisfaction.trav.impAussi 0.54156
Equilibre.trav.impMoins 0.73727
Satisfaction.trav.impMoins 0.66621
Equilibre.trav.impPeu -1.54722
Satisfaction.trav.impPeu -1.47191
SE t value
Equilibre.(Intercept) 3.08681 0.3043
Satisfaction.(Intercept) 2.99811 0.2472
Equilibre.sexeHomme 0.32599 -0.7455
Satisfaction.sexeHomme 0.30959 -0.8844
Equilibre.etudSecondaire 0.58700 -0.7121
Satisfaction.etudSecondaire 0.62122 -0.4279
Equilibre.etudTechnique/Professionnel 0.53999 -0.8835
Satisfaction.etudTechnique/Professionnel 0.56932 -0.4143
Equilibre.etudSupérieur 0.53037 -1.0856
Satisfaction.etudSupérieur 0.56015 0.6570
Equilibre.etudmanquant 5.27928 -0.0613
Satisfaction.etudmanquant 5.15549 -0.1267
Equilibre.grpage[25,45) 0.60719 0.9998
Satisfaction.grpage[25,45) 0.63359 0.7409
Equilibre.grpage[45,65) 0.66554 0.8713
Satisfaction.grpage[45,65) 0.67234 0.7864
Equilibre.grpage[65,99] 15.19731 -0.2110
Satisfaction.grpage[65,99] 16.34759 0.7096
Equilibre.trav.impAussi 2.99947 0.1419
Satisfaction.trav.impAussi 2.94534 0.1839
Equilibre.trav.impMoins 2.97232 0.2480
Satisfaction.trav.impMoins 2.91825 0.2283
Equilibre.trav.impPeu 3.09324 -0.5002
Satisfaction.trav.impPeu 3.05773 -0.4814
Pr(>|t|)
Equilibre.(Intercept) 0.7617
Satisfaction.(Intercept) 0.8054
Equilibre.sexeHomme 0.4582
Satisfaction.sexeHomme 0.3793
Equilibre.etudSecondaire 0.4786
Satisfaction.etudSecondaire 0.6700
Equilibre.etudTechnique/Professionnel 0.3798
Satisfaction.etudTechnique/Professionnel 0.6798
Equilibre.etudSupérieur 0.2811
Satisfaction.etudSupérieur 0.5132
Equilibre.etudmanquant 0.9513
Satisfaction.etudmanquant 0.8995
Equilibre.grpage[25,45) 0.3206
Satisfaction.grpage[25,45) 0.4611
Equilibre.grpage[45,65) 0.3863
Satisfaction.grpage[45,65) 0.4341
Equilibre.grpage[65,99] 0.8334
Satisfaction.grpage[65,99] 0.4801
Equilibre.trav.impAussi 0.8876
Satisfaction.trav.impAussi 0.8546
Equilibre.trav.impMoins 0.8048
Satisfaction.trav.impMoins 0.8200
Equilibre.trav.impPeu 0.6184
Satisfaction.trav.impPeu 0.6316 2.5 %
Equilibre.(Intercept) -5.2084508
Satisfaction.(Intercept) -5.2299773
Equilibre.sexeHomme -0.8923106
Satisfaction.sexeHomme -0.8904071
Equilibre.etudSecondaire -1.5871351
Satisfaction.etudSecondaire -1.5030519
Equilibre.etudTechnique/Professionnel -1.5525615
Satisfaction.etudTechnique/Professionnel -1.3697625
Equilibre.etudSupérieur -1.6321174
Satisfaction.etudSupérieur -0.7476291
Equilibre.etudmanquant -10.8380480
Satisfaction.etudmanquant -10.9214744
Equilibre.grpage[25,45) -0.6022290
Satisfaction.grpage[25,45) -0.7924897
Equilibre.grpage[45,65) -0.7456414
Satisfaction.grpage[45,65) -0.8103550
Equilibre.grpage[65,99] -33.4748095
Satisfaction.grpage[65,99] -20.9581253
Equilibre.trav.impAussi -5.5484453
Satisfaction.trav.impAussi -5.3245967
Equilibre.trav.impMoins -5.1826190
Satisfaction.trav.impMoins -5.1459947
Equilibre.trav.impPeu -7.7079314
Satisfaction.trav.impPeu -7.5619188
97.5 %
Equilibre.(Intercept) 7.0873883
Satisfaction.(Intercept) 6.7125164
Equilibre.sexeHomme 0.4062276
Satisfaction.sexeHomme 0.3427945
Equilibre.etudSecondaire 0.7510904
Satisfaction.etudSecondaire 0.9714624
Equilibre.etudTechnique/Professionnel 0.5984006
Satisfaction.etudTechnique/Professionnel 0.8980555
Equilibre.etudSupérieur 0.4805406
Satisfaction.etudSupérieur 1.4836530
Equilibre.etudmanquant 10.1911288
Satisfaction.etudmanquant 9.6146107
Equilibre.grpage[25,45) 1.8164309
Satisfaction.grpage[25,45) 1.7313012
Equilibre.grpage[45,65) 1.9054190
Satisfaction.grpage[45,65) 1.8678141
Equilibre.grpage[65,99] 27.0613398
Satisfaction.grpage[65,99] 44.1599641
Equilibre.trav.impAussi 6.3994661
Satisfaction.trav.impAussi 6.4077216
Equilibre.trav.impMoins 6.6571506
Satisfaction.trav.impMoins 6.4784050
Equilibre.trav.impPeu 4.6134952
Satisfaction.trav.impPeu 4.6180931Régression ordinale
Pour un modèle ordinal, il existe une version simplifiée des modèles ordinaux directement disponible dans survey via la fonction svyolr.
Call:
svyolr(trav.satisf ~ sexe + etud + trav.imp, design = dw)
Coefficients:
Value Std. Error
sexeHomme -0.1328026100 0.1545640
etudSecondaire -0.0427151234 0.2751085
etudTechnique/Professionnel 0.0004261287 0.2492533
etudSupérieur 0.6424698737 0.2593446
etudmanquant -0.4694599623 0.5033490
trav.impAussi 0.1207125976 0.5044264
trav.impMoins 0.0526740003 0.4895782
trav.impPeu -1.5303889517 0.7215699
t value
sexeHomme -0.859207986
etudSecondaire -0.155266460
etudTechnique/Professionnel 0.001709621
etudSupérieur 2.477282672
etudmanquant -0.932672851
trav.impAussi 0.239306656
trav.impMoins 0.107590577
trav.impPeu -2.120915790
Intercepts:
Value Std. Error t value
Insatisfaction|Equilibre -2.0392 0.5427 -3.7577
Equilibre|Satisfaction 0.2727 0.5306 0.5140
(952 observations effacées parce que manquantes) 2.5 % 97.5 %
sexeHomme -0.4357425 0.1701372
etudSecondaire -0.5819179 0.4964876
etudTechnique/Professionnel -0.4881013 0.4889536
etudSupérieur 0.1341638 1.1507759
etudmanquant -1.4560059 0.5170860
trav.impAussi -0.8679450 1.1093702
trav.impMoins -0.9068816 1.0122296
trav.impPeu -2.9446399 -0.1161380
Insatisfaction|Equilibre -3.1027595 -0.9755811
Equilibre|Satisfaction -0.7672025 1.3126335Une alternative est d’avoir recours, comme pour la régression multinomiale, aux poids de réplication et à la fonction svyclm implémentée dans l’extension svrepmisc.
dwr <- as.svrepdesign(dw, type = "bootstrap", replicates = 100)
library(svrepmisc)
rego_alt <- svyclm(trav.satisf ~ sexe + etud + trav.imp, design = dwr)Warning: (-1) Model failed to converge with max|grad| = 0.00115453 (tol = 1e-06)
In addition: step factor reduced below minimumWarning: (-1) Model failed to converge with max|grad| = 0.000312696 (tol = 1e-06)
In addition: step factor reduced below minimumWarning: (-1) Model failed to converge with max|grad| = 0.000257021 (tol = 1e-06)
In addition: step factor reduced below minimumWarning: (-1) Model failed to converge with max|grad| = 2.88767e-05 (tol = 1e-06)
In addition: step factor reduced below minimumWarning: (-1) Model failed to converge with max|grad| = 0.000986098 (tol = 1e-06)
In addition: step factor reduced below minimum Coefficient SE t value
Insatisfaction|Equilibre -2.03917466 0.55149786 -3.6975
Equilibre|Satisfaction 0.27271800 0.54289138 0.5023
sexeHomme -0.13280477 0.14490801 -0.9165
etudSecondaire -0.04271403 0.31046925 -0.1376
etudTechnique/Professionnel 0.00042809 0.27099684 0.0016
etudSupérieur 0.64247607 0.23962101 2.6812
etudmanquant -0.46945975 0.51160937 -0.9176
trav.impAussi 0.12071087 0.52813124 0.2286
trav.impMoins 0.05267146 0.50191026 0.1049
trav.impPeu -1.53039056 0.78653870 -1.9457
Pr(>|t|)
Insatisfaction|Equilibre 0.000374 ***
Equilibre|Satisfaction 0.616653
sexeHomme 0.361866
etudSecondaire 0.890881
etudTechnique/Professionnel 0.998743
etudSupérieur 0.008725 **
etudmanquant 0.361274
trav.impAussi 0.819728
trav.impMoins 0.916655
trav.impPeu 0.054808 .
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 2.5 % 97.5 %
Insatisfaction|Equilibre -3.1348214 -0.94352790
Equilibre|Satisfaction -0.8058305 1.35126648
sexeHomme -0.4206898 0.15508028
etudSecondaire -0.6595154 0.57408732
etudTechnique/Professionnel -0.5379544 0.53881061
etudSupérieur 0.1664271 1.11852503
etudmanquant -1.4858611 0.54694156
trav.impAussi -0.9285140 1.16993575
trav.impMoins -0.9444609 1.04980380
trav.impPeu -3.0929870 0.03220584Il existe également une fonction
add.NAfournie de base avec R etaddNAstrfournie parquestionr.↩︎Pour plus de détails, voir http://www.spc.univ-lyon1.fr/polycop/odds%20ratio.htm.↩︎
Cette extension est livrée avec de nombreuses vignettes dont une vignette d’introduction présentant le fonctionnement des différentes fonctions.↩︎
Il existe également des méthodes de sélection ascendante pas à pas, mais nous les aborderons pas ici.↩︎
Une alternative est d’avoir recours à l’extension
mlogitque nous n’aborderons pas ici. Voir http://www.ats.ucla.edu/stat/r/dae/mlogit.htm (en anglais) pour plus de détails.↩︎Voir le chapitre dédié aux données pondérées.↩︎
Compatibilité qui pourra éventuellement être introduite dans une future version de l’extension.↩︎

