Ce chapitre vise à illustrer l’utilisation de la notation formule de R, qui désigne l’emploi de cette notation par l’expression formula. Cette notation est utilisée par de très nombreuses fonctions de R : on en a notamment vu plusieurs exemples dans le chapitre sur les graphiques bivariés, car l’extension ggplot2 se sert de cette notation dans ses paramètres facet_wrap et facet_grid.

Dans ce chapitre, on verra comment se servir de la notation formule dans deux contextes différents. D’une part, on verra que deux fonctions basiques de R se servent de cette notation pour produire des tableaux croisés et des statistiques bivariées. D’autre part, on verra que l’extension lattice se sert de cette notation pour créer des graphiques panelisés, dits graphiques à petits multiples.

Dans plusieurs autres chapitres, les opérations décrites ci-dessus sont effectuées avec les extensions dplyr d’une part, et ggplot2 d’autre part. On se servira également de ces extensions dans ce chapitre, de manière à mener une comparaison des différentes manières d’effectuer certaines opérations dans R, avec ou sans la notation formule :

library(dplyr)
library(ggplot2)

Statistiques descriptives

Les premiers exemples de ce chapitre montrent l’utilisation de cette notation pour produire des tableaux croisés et des statistiques descriptives. Le jeu de données utilisé, hdv2003, a déjà été utilisé dans plusieurs chapitres, et font partie de l’extension questionr. Chargeons cette extension et le jeu de données hdv2003 :

library(questionr)
data(hdv2003)

Pour rappel, ce jeu de données contient des individus, leur âge, leur statut professionnel, et le nombre d’heures quotidiennes passées à regarder la télévision.

glimpse(hdv2003, 75)
Rows: 2,000
Columns: 20
$ id            <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, …
$ age           <int> 28, 23, 59, 34, 71, 35, 60, 47, 20, 28, 65, 47, 63,…
$ sexe          <fct> Femme, Femme, Homme, Homme, Femme, Femme, Femme, Ho…
$ nivetud       <fct> "Enseignement superieur y compris technique superie…
$ poids         <dbl> 2634.3982, 9738.3958, 3994.1025, 5731.6615, 4329.09…
$ occup         <fct> "Exerce une profession", "Etudiant, eleve", "Exerce…
$ qualif        <fct> Employe, NA, Technicien, Technicien, Employe, Emplo…
$ freres.soeurs <int> 8, 2, 2, 1, 0, 5, 1, 5, 4, 2, 3, 4, 1, 5, 2, 3, 4, …
$ clso          <fct> Oui, Oui, Non, Non, Oui, Non, Oui, Non, Oui, Non, O…
$ relig         <fct> Ni croyance ni appartenance, Ni croyance ni apparte…
$ trav.imp      <fct> Peu important, NA, Aussi important que le reste, Mo…
$ trav.satisf   <fct> Insatisfaction, NA, Equilibre, Satisfaction, NA, Eq…
$ hard.rock     <fct> Non, Non, Non, Non, Non, Non, Non, Non, Non, Non, N…
$ lecture.bd    <fct> Non, Non, Non, Non, Non, Non, Non, Non, Non, Non, N…
$ peche.chasse  <fct> Non, Non, Non, Non, Non, Non, Oui, Oui, Non, Non, N…
$ cuisine       <fct> Oui, Non, Non, Oui, Non, Non, Oui, Oui, Non, Non, O…
$ bricol        <fct> Non, Non, Non, Oui, Non, Non, Non, Oui, Non, Non, O…
$ cinema        <fct> Non, Oui, Non, Oui, Non, Oui, Non, Non, Oui, Oui, O…
$ sport         <fct> Non, Oui, Oui, Oui, Non, Oui, Non, Non, Non, Oui, N…
$ heures.tv     <dbl> 0.0, 1.0, 0.0, 2.0, 3.0, 2.0, 2.9, 1.0, 2.0, 2.0, 1…

Tableaux croisés avec xtabs

Utilisons, pour ce premier exemple, la variable occup du jeu de données hdv2003, qui correspond au statut professionnel des individus inclus dans l’échantillon. La fonction de base pour compter les individus par statut est la fonction table :

table(hdv2003$occup)

Exerce une profession               Chomeur 
                 1049                   134 
      Etudiant, eleve              Retraite 
                   94                   392 
  Retire des affaires              Au foyer 
                   77                   171 
        Autre inactif 
                   83

Avec la fonction xtabs, le même résultat est produit à partir de la notation suivante :

xtabs(~occup, data = hdv2003)
occup
Exerce une profession               Chomeur 
                 1049                   134 
      Etudiant, eleve              Retraite 
                   94                   392 
  Retire des affaires              Au foyer 
                   77                   171 
        Autre inactif 
                   83

Le premier argument est une formule, au sens où R entend cette expression. Le second argument, data, correspond au jeu de données auquel la formule doit être appliquée. On pourra se passer d’écrire explicitement cet argument dans les exemples suivants.

L’avantage de la fonction xtabs n’est pas évident dans ce premier exemple. En réalité, cette fonction devient utile lorsque l’on souhaite construire un ou plusieurs tableau(x) croisé(s). Par exemple, pour croiser la variable occup avec la variable sexe, une solution constiste à écrire :

with(hdv2003, table(occup, sexe))
                       sexe
occup                   Homme Femme
  Exerce une profession   520   529
  Chomeur                  54    80
  Etudiant, eleve          48    46
  Retraite                208   184
  Retire des affaires      39    38
  Au foyer                  0   171
  Autre inactif            30    53

Ou alors, ce qui revient au même :

table(hdv2003$occup, hdv2003$sexe)

Avec xtabs, la même opération s’écrit de la manière suivante :

xtabs(~ occup + sexe, hdv2003)
                       sexe
occup                   Homme Femme
  Exerce une profession   520   529
  Chomeur                  54    80
  Etudiant, eleve          48    46
  Retraite                208   184
  Retire des affaires      39    38
  Au foyer                  0   171
  Autre inactif            30    53

Cette écriture est plus courte que le code équivalent dans dplyr :

hdv2003 %>%
  group_by(occup) %>%
  summarise(
    Homme = sum(sexe == "Homme"),
    Femme = sum(sexe == "Femme")
  )

Par contre, on pourra éventuellement utiliser count de dplyr. ATTENTION : le format du résultat ne sera pas le même.

hdv2003 %>%
  group_by(occup) %>%
  dplyr::count(sexe)

Pour un tableau croisé joliment mis en forme, on pourra avoir recours à tbl_cross de gtsummary.

library(gtsummary)
hdv2003 %>%
  tbl_cross(row = "occup", col = "sexe", percent = "row")
sexe Total
Homme Femme
occup
    Exerce une profession 520 (50%) 529 (50%) 1 049 (100%)
    Chomeur 54 (40%) 80 (60%) 134 (100%)
    Etudiant, eleve 48 (51%) 46 (49%) 94 (100%)
    Retraite 208 (53%) 184 (47%) 392 (100%)
    Retire des affaires 39 (51%) 38 (49%) 77 (100%)
    Au foyer 0 (0%) 171 (100%) 171 (100%)
    Autre inactif 30 (36%) 53 (64%) 83 (100%)
Total 899 (45%) 1 101 (55%) 2 000 (100%)

De plus, xtabs permet de créer plusieurs tableaux croisés en une seule formule :

xtabs(~ occup + sexe + trav.imp, hdv2003)
, , trav.imp = Le plus important

                       sexe
occup                   Homme Femme
  Exerce une profession    13    16
  Chomeur                   0     0
  Etudiant, eleve           0     0
  Retraite                  0     0
  Retire des affaires       0     0
  Au foyer                  0     0
  Autre inactif             0     0

, , trav.imp = Aussi important que le reste

                       sexe
occup                   Homme Femme
  Exerce une profession   159   100
  Chomeur                   0     0
  Etudiant, eleve           0     0
  Retraite                  0     0
  Retire des affaires       0     0
  Au foyer                  0     0
  Autre inactif             0     0

, , trav.imp = Moins important que le reste

                       sexe
occup                   Homme Femme
  Exerce une profession   328   380
  Chomeur                   0     0
  Etudiant, eleve           0     0
  Retraite                  0     0
  Retire des affaires       0     0
  Au foyer                  0     0
  Autre inactif             0     0

, , trav.imp = Peu important

                       sexe
occup                   Homme Femme
  Exerce une profession    20    32
  Chomeur                   0     0
  Etudiant, eleve           0     0
  Retraite                  0     0
  Retire des affaires       0     0
  Au foyer                  0     0
  Autre inactif             0     0

Cet exemple permet simplement de réaliser que la variable trav.imp, qui contient les réponses à une question portant sur l’importance du travail, n’a été mesurée (c’est-à-dire que la question n’a été posée) qu’aux seuls individus actifs de l’échantillon.

Statistiques bivariées avec aggregate

aggregate(heures.tv ~ sexe, mean, data = hdv2003)

Ici, le premier argument est à nouveau une formule. Le second argument correspond à la statistique descriptive que l’on souhaite obtenir, et le dernier argument indique le jeu de données auquel appliquer les deux autres arguments. On peut d’ailleurs obtenir le même résultat en respectant de manière plus stricte l’ordre des arguments dans la syntaxe de la fonction aggregate :

aggregate(heures.tv ~ sexe, hdv2003, mean)

Cette écriture est, à nouveau, plus compacte que le code équivalent dans dplyr, qui demande de spécifier le retrait des valeurs manquantes :

hdv2003 %>
  group_by(sexe) %>%
  summarise(heures.tv = mean(heures.tv, na.rm = TRUE))

À nouveau, on va pouvoir combiner plusieurs variables dans la formule que l’on passe à aggregate, ce qui va permettre d’obtenir la moyenne des heures de télévision quotidiennes par sexe et par statut professionnel :

aggregate(heures.tv ~ sexe + occup, hdv2003, mean)

La même opération dplyr :

hdv2003 %>%
  group_by(occup, sexe) %>%
  summarise(heures.tv = mean(heures.tv, na.rm = TRUE))

La fonction aggregate permet bien sûr d’utiliser une autre fonction que la moyenne, comme dans cet exemple, suivi de son équivalent avec dplyr :

# âge médian par sexe et statut professionnel
aggregate(age ~ sexe + occup, hdv2003, median)
# code équivalent avec l'extension 'dplyr'
hdv2003 %>%
  group_by(occup, sexe) %>%
  summarise(age = median(age, na.rm = TRUE))

Si, comme dans le cas de summarise, on souhaite passer des arguments supplémentaires à la fonction median, il suffit de les lister à la suite du nom de la fonction. Par exemple, on écrirait : aggregate(age ~ sexe + occup, hdv2003, median, na.rm = TRUE). Ceci étant, aggregate utilise par défaut l’option na.action = na.omit, donc il est bon de se rappeler que l’on peut désactiver cette option en utilisant l’option na.action = na.pass, ce qui permet éventuellement de conserver des lignes vides dans le tableau de résultat.

La fonction aggregate permet, par ailleurs, d’obtenir des résultats à plusieurs colonnes. Dans l’exemple ci-dessus, on illustre ce principe avec la fonction range, qui renvoie deux résultats (la valeur minimale et la valeur maximale de la variable, qui est toujours la variable age), chacun présentés dans une colonne :

aggregate(age ~ sexe + occup, hdv2003, range)
    sexe                 occup age.1 age.2
1  Homme Exerce une profession    18    63
2  Femme Exerce une profession    18    67
3  Homme               Chomeur    18    63
4  Femme               Chomeur    18    63
5  Homme       Etudiant, eleve    18    34
6  Femme       Etudiant, eleve    18    35
7  Homme              Retraite    48    92
8  Femme              Retraite    41    96
9  Homme   Retire des affaires    57    91
10 Femme   Retire des affaires    57    93
11 Femme              Au foyer    22    90
12 Homme         Autre inactif    39    71
13 Femme         Autre inactif    19    97

Cette fonction ne peut pas être facilement écrite dans dplyr sans réécrire chacune des colonnes, ce que le bloc de code suivant illustre. On y gagne en lisibilité dans les intitulés de colonnes :

hdv2003 %>%
  group_by(occup, sexe) %>%
  summarise(
    min = min(age, na.rm = TRUE),
    max = max(age, na.rm = TRUE)
  )

Depuis la version 1.0.0 de dplyr, summarise accepte maintenant des fonctions pouvant renvoyer plusieurs valeurs, créant ainsi autant de lignes (voir https://www.tidyverse.org/blog/2020/03/dplyr-1-0-0-summarise/).

hdv2003 %>%
  group_by(occup, sexe) %>%
  summarise(age = range(age, na.rm = TRUE), type = c("min", "max"))
Warning: Returning more (or less) than 1 row per `summarise()` group
was deprecated in dplyr 1.1.0.
ℹ Please use `reframe()` instead.
ℹ When switching from `summarise()` to `reframe()`,
  remember that `reframe()` always returns an ungrouped
  data frame and adjust accordingly.
`summarise()` has grouped output by 'occup', 'sexe'. You
can override using the `.groups` argument.

On pourrait de même définir sa propre fonction et la passer à aggregate :

f <- function(x) c(mean = mean(x, na.rm = TRUE), sd = sd(x, na.rm = TRUE))
aggregate(age ~ sexe + occup, hdv2003, f)
    sexe                 occup  age.mean    age.sd
1  Homme Exerce une profession 41.461538 10.438113
2  Femme Exerce une profession 40.710775 10.203864
3  Homme               Chomeur 38.925926 13.256329
4  Femme               Chomeur 38.012500 11.648321
5  Homme       Etudiant, eleve 20.895833  2.926326
6  Femme       Etudiant, eleve 21.586957  3.249452
7  Homme              Retraite 68.418269  8.018882
8  Femme              Retraite 69.510870  8.228957
9  Homme   Retire des affaires 71.179487  7.687556
10 Femme   Retire des affaires 73.789474  7.651737
11 Femme              Au foyer 50.730994 15.458412
12 Homme         Autre inactif 54.166667  6.597196
13 Femme         Autre inactif 59.962264 14.660206

Mais on réalisera vite une des limitations de aggregate dans ce cas-là : le tableau retourné ne contient pas 4 colonnes, mais 3 uniquement, ce que l’on peut vérifier à l’aide de dim ou str.

str(aggregate(age ~ sexe + occup, hdv2003, f))
'data.frame':   13 obs. of  3 variables:
 $ sexe : Factor w/ 2 levels "Homme","Femme": 1 2 1 2 1 2 1 2 1 2 ...
 $ occup: Factor w/ 7 levels "Exerce une profession",..: 1 1 2 2 3 3 4 4 5 5 ...
 $ age  : num [1:13, 1:2] 41.5 40.7 38.9 38 20.9 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : NULL
  .. ..$ : chr [1:2] "mean" "sd"

Pour ce type d’opération, dans lequel on souhaite récupérer plusieurs variables calculées afin de travailler sur ces données agrégées soit dans le cadre d’opérations numériques soit de constructions graphiques, dplyr ou Hmisc s’avèrent plus commodes. Voici un exemple avec summarize de l’extension Hmisc :

library(Hmisc, quietly = TRUE)

Attachement du package : 'Hmisc'
L'objet suivant est masqué depuis 'package:srvyr':

    summarize
L'objet suivant est masqué depuis 'package:gt':

    html
L'objet suivant est masqué depuis 'package:survey':

    deff
L'objet suivant est masqué depuis 'package:ggdendro':

    label
Les objets suivants sont masqués depuis 'package:dplyr':

    src, summarize
Les objets suivants sont masqués depuis 'package:questionr':

    describe, wtd.mean, wtd.table, wtd.var
Les objets suivants sont masqués depuis 'package:base':

    format.pval, units
with(hdv2003, summarize(age, llist(sexe, occup), f))

Notons que Hmisc offre déjà une telle fonction (smean.sd), ce qui nous aurait épargné d’écrire notre propre fonction, f, et il en existe bien d’autres. Voici un exemple avec des intervalles de confiance estimés par bootstrap :

with(hdv2003, summarize(age, llist(sexe, occup), smean.cl.boot))

Et un exemple avec dplyr.

hdv2003 %>%
  group_by(sexe, occup) %>%
  summarise(
    tibble(
      age_mean = mean(age, na.rm = TRUE),
      age_sd = sd(age, na.rm = TRUE)
    )
  )
`summarise()` has grouped output by 'sexe'. You can
override using the `.groups` argument.

Enfin, il est également possible d’utiliser plusieurs variables numériques à gauche de l’opérateur ~. En voici une illustration :

aggregate(cbind(age, poids) ~ sexe + occup, hdv2003, mean)

Panels graphiques avec lattice

Les exemples suivants montreront ensuite comment la notation formule peut servir à produire des graphiques par panel avec l’extension lattice.

library(lattice)

L’extension lattice présente l’avantage d’être installée par défaut avec R. Il n’est donc pas nécessaire de l’installer préalablement.

Chargeons les mêmes données que le chapitre sur les graphiques bivariés.

# charger l'extension lisant le format CSV
library(readr)

# emplacement souhaité pour le jeu de données
file <- "data/debt.csv"

# télécharger le jeu de données s'il n'existe pas
if (!file.exists(file)) {
  download.file("http://www.stat.cmu.edu/~cshalizi/uADA/13/hw/11/debt.csv",
    file,
    mode = "wb"
  )
}

# charger les données dans l'objet 'debt'
debt <- read_csv(file)
New names:
Rows: 1171 Columns: 5
── Column specification
──────────────────────────────────── Delimiter: "," chr
(1): Country dbl (4): ...1, Year, growth, ratio
ℹ Use `spec()` to retrieve the full column specification
for this data. ℹ Specify the column types or set
`show_col_types = FALSE` to quiet this message.
• `` -> `...1`

Rejetons rapidement un coup d’oeil à ces données, qui sont structurées par pays (variable Country) et par année (variable Year). On y trouve deux variables, growth (le taux de croissance du produit intérieur brut réel), et ratio (le ratio entre la dette publique et le produit intérieur brut), ainsi qu’une première colonne vide, ne contenant que des numéros lignes, dont on va se débarrasser :

# inspection des données
glimpse(debt, 75)
Rows: 1,171
Columns: 5
$ ...1    <dbl> 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 15…
$ Country <chr> "Australia", "Australia", "Australia", "Australia", "Aust…
$ Year    <dbl> 1946, 1947, 1948, 1949, 1950, 1951, 1952, 1953, 1954, 195…
$ growth  <dbl> -3.5579515, 2.4594746, 6.4375341, 6.6119938, 6.9202012, 4…
$ ratio   <dbl> 190.41908, 177.32137, 148.92981, 125.82870, 109.80940, 87…
# suppression de la première colonne
debt <- debt[, -1]

Visualisation bivariée

Le même graphique s’écrit de la manière suivante avec l’extension lattice :

xyplot(growth ~ Year, data = debt)

Visualisation par petits multiples

Appliquons désormais la même visualisation par petits multiples que vue dans le chapitre :

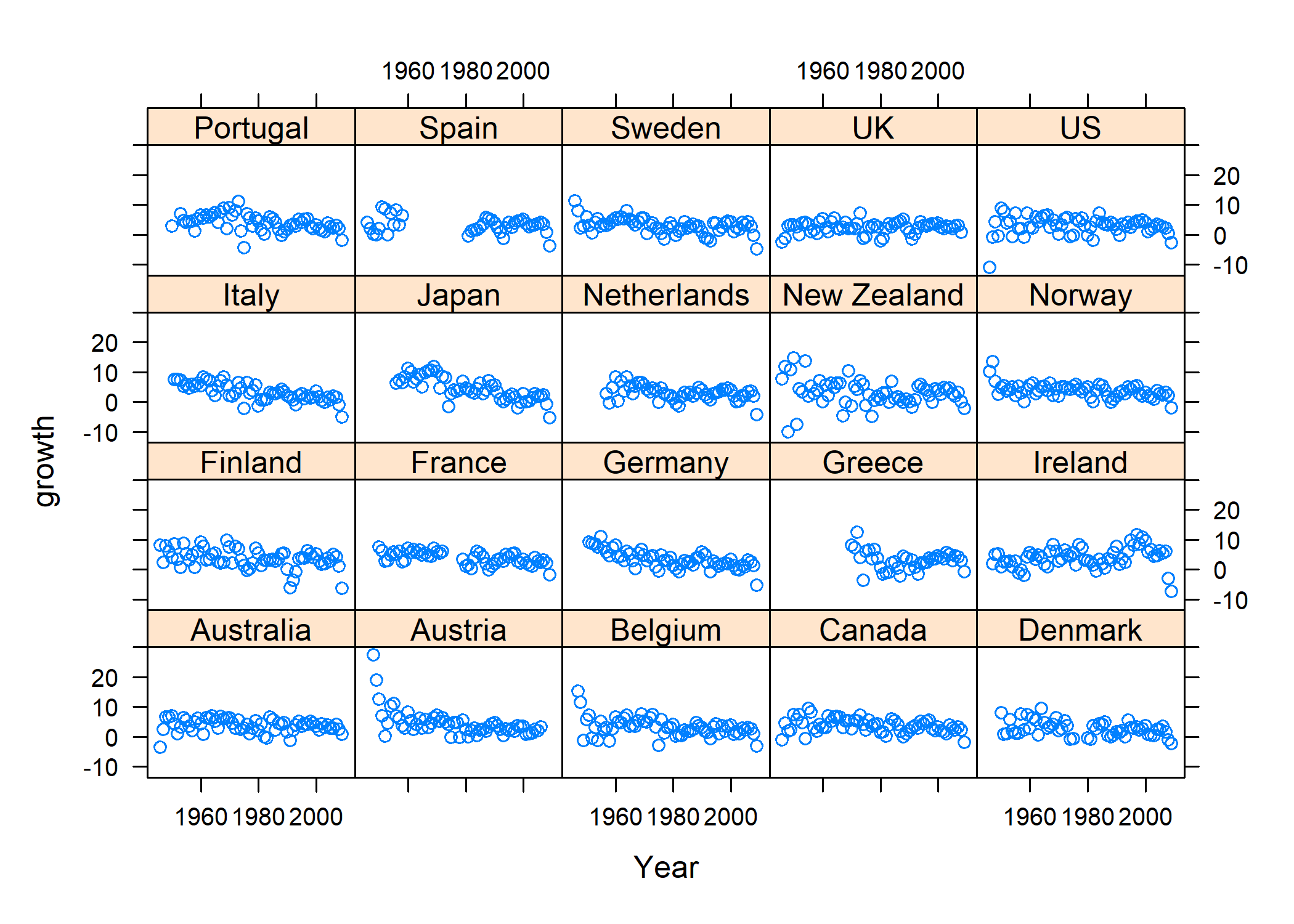
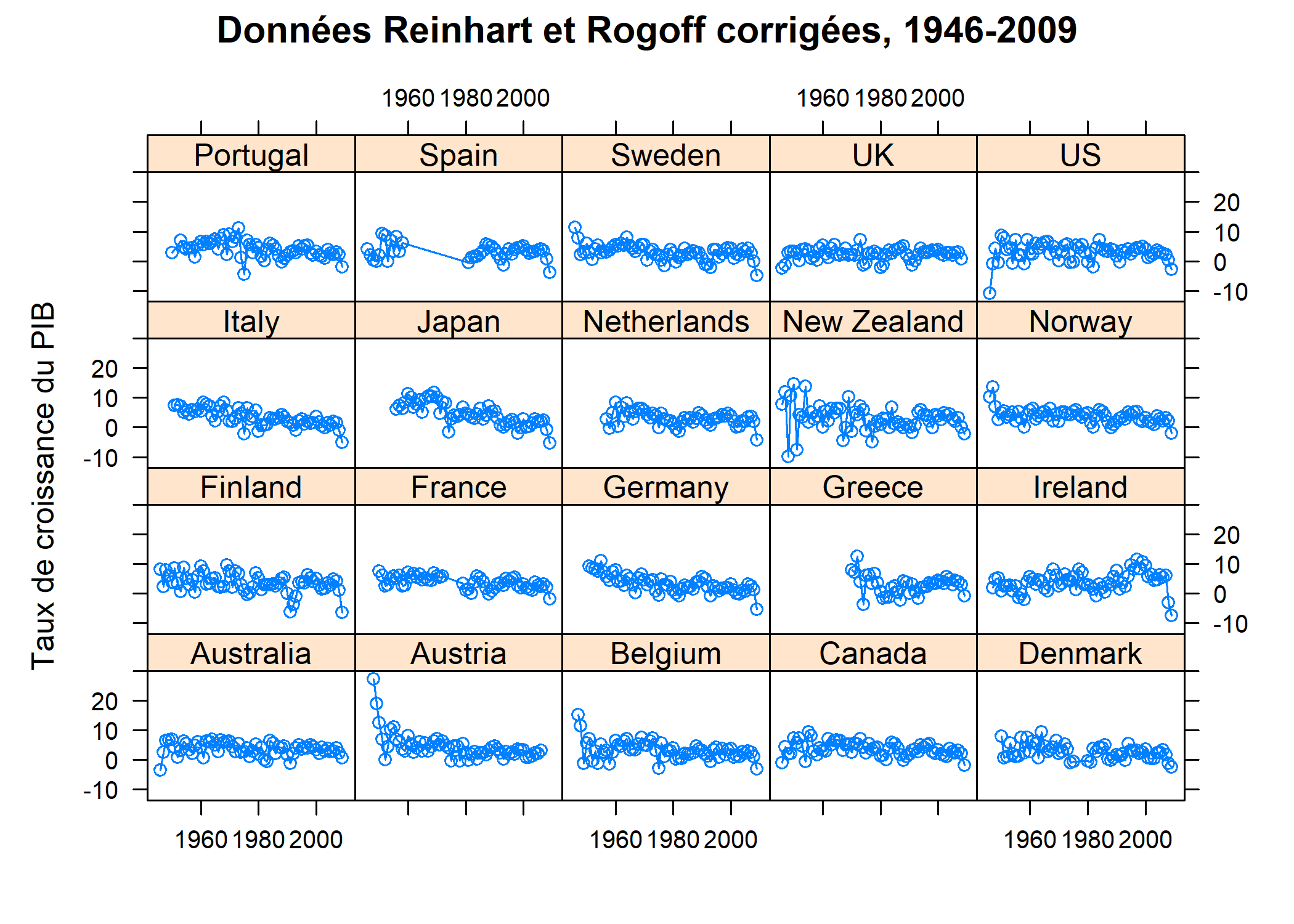
xyplot(growth ~ Year | Country, data = debt)

Enfin, rajoutons quelques options au graphique, afin de montrer comment l’extension lattice fonctionne :

xyplot(growth ~ Year | Country,
  type = c("o", "l"),
  main = "Données Reinhart et Rogoff corrigées, 1946-2009",
  ylab = "Taux de croissance du PIB",
  xlab = NULL,
  data = debt
)

Spécifier des modèles

Les formules R

En réalité, la notation par formule qu’utilise R est celle proposée par Wilkinson et al. dans les années 70 pour schématiser la relation entre plusieurs variables dans un plan d’expérience. Plus spécifiquement, l’idée revient à exprimer une relation fonctionnelle, symbolisée par l’opérateur ~, entre une variable réponse y et une ou plusieurs variables explicatives. Disons, pour simplifier, que y est une variable d’intérêt (numérique ou facteur selon le type de modèle), x une variable numérique et que a et b sont des variables catégorielles (des facteurs dans le langage R). Voici les principales relations auxquelles on peut s’intéresser dans un modèle statistique :

  • y ~ x : régression simple,
  • y ~ x + 0 : idem avec suppression du terme d’ordonnée à l’origine,
  • y ~ a + b : régresse avec deux effets principaux indépendants,
  • y ~ a * b : idem avec interaction (équivalent à 1 + a + b + a:b),
  • y ~ a / b : idem en considérant une relation d’emboîtement (équivalent à 1 + a + b + a %in% b).

L’opérateur | est quant à lui utilisé par l’extension lme4 dans le cadre de modèles mixtes avec effets aléatoires.

Voir le chapitre dédié à la régression logistique pour des exemples de modèles multivariés et le chapitre dédié aux effets d’interaction pour plus de détails sur cette notion.

Pour aller plus loin

Comme vient de le voir dans ce chapitre, la notation formule apparaît çà et là dans les différentes fonctions de R est de ses extensions. Il est par conséquent utile d’en connaître les rudiments, et en particulier les opérateurs ~ (tilde) et +, ne serait-ce que pour pouvoir se servir des différentes fonctions présentées sur cette page. Le chapitre lattice et les formules fournit plus de détails sur ces aspects.

La notation formule devient cruciale dès que l’on souhaite rédiger des modèles : la formule y ~ x, par exemple, qui est équivalente à la formule y ~ 1 + x, correspond à l’équation mathématique Y = a + bX. On trouvera de nombreux exemples d’usage de cette notation dans les chapitres consacrés, notamment, à la régression linéaire ou à la régression logistique.

De la même manière, l’opérateur | (pipe) utilisé par l’extension lattice joue aussi un rôle très important dans la rédaction de modèles multi-niveaux, où il sert à indiquer les variables à pentes ou à coefficients aléatoires. Ces modèles sont présentés dans un chapitre dédié.