Classification ascendante hiérarchique (CAH)

Calculer une matrice des distances
Calcul du dendrogramme
Découper le dendrogramme
Caractériser la typologie
CAH avec l’extension FactoMineR

Une version actualisée de ce chapitre est disponible sur guide-R : Classification ascendante hiérarchique

Ce chapitre est évoqué dans le webin-R #12 (Classification ascendante hiérarchique sur YouTube.

Pour une introduction didactique et en français à la classification, voir ce billet de Philippe Cibois sur Hypothses.org.

Il existe de nombreuses techniques statistiques visant à partinionner une population en différentes classes ou sous-groupes. La classification ascendante hiérarchique (CAH) est l’une d’entre elles. On cherche à ce que les individus regroupés au sein d’une même classe (homogénéité intra-classe) soient le plus semblables possibles tandis que les classes soient le plus dissemblables (hétérogénéité inter-classe).

Le principe de la CAH est de rassembler des individus selon un critère de ressemblance défini au préalable qui s’exprimera sous la forme d’une matrice de distances, exprimant la distance existant entre chaque individu pris deux à deux. Deux observations identiques auront une distance nulle. Plus les deux observations seront dissemblables, plus la distance sera importante. La CAH va ensuite rassembler les individus de manière itérative afin de produire un dendrogramme ou arbre de classification. La classification est ascendante car elle part des observations individuelles ; elle est hiérarchique car elle produit des classes ou groupes de plus en plus vastes, incluant des sous-groupes en leur sein. En découpant cet arbre à une certaine hauteur choisie, on produira la partition désirée.

On trouvera également de nombreux supports de cours en français sur la CAH sur le site de François Gilles Carpentier : http://pagesperso.univ-brest.fr/~carpenti/.

Calculer une matrice des distances

La notion de ressemblance entre observations est évaluée par une distance entre individus. Plusieurs type de ditances existent selon les données utilisées.

Il existe de nombreuses distances mathématiques pour les variables quantitatives (euclidiennes, Manhattan…) que nous n’aborderons pas ici¹. La plupart peuvent être calculées avec la fonction dist.

Usuellement, pour un ensemble de variables qualitatives, on aura recours à la distance du Φ² qui est celle utilisée pour l’analyse des correspondances multiples (voir le chapitre dédié). Avec l’extension ade4, la distance du Φ² s’obtient avec la fonction dist.dudi². Le cas particulier de la CAH avec l’extension FactoMineR sera abordée dans une section spécifique ci-après. Nous évoquerons également la distance de Gower qui peut s’appliquer à un ensemble de variables à la fois qualitatives et quantitatives et qui se calcule avec la fonction daisy de l’extension cluster. Enfin, dans le chapitre sur l’analyse de séquences, nous verrons également la fonction seqdist (extension TraMineR) permettant de calculer une distance entre séquences.

Distance de Gower

En 1971, Gower a proposé un indice de similarité qui porte son nom³. L’objectif de cet indice consiste à mesurer dans quelle mesure deux individus sont semblables. L’indice de Gower varie entre 0 et 1. Si l’indice vaut 1, les deux individus sont identiques. À l’opposé, s’il vaut 0, les deux individus considérés n’ont pas de point commun. Si l’on note S_g l’indice de similarité de Gower, la distance de Gower D_g s’obtient simplement de la manière suivante : D_g = 1 - S_g. Ainsi, la distance sera nulle entre deux individus identiques et elle sera égale à 1 entre deux individus totalement différents. Cette distance s’obtient sous R avec la fonction daisy du package cluster.

L’indice de similarité de Gower entre deux individus x₁ et x₂ se calcule de la manière suivante :

$S_{g} (x_{1}, x_{2}) = \frac{1}{p} \sum_{j = 1}^{p} s_{12 j}$

p représente le nombre total de caractères (ou de variables) descriptifs utilisés pour comparer les deux individus⁴. s_12j représente la similarité partielle entre les individus 1 et 2 concernant le descripteur j. Cette similarité partielle se calcule différemment s’il s’agit d’une variable qualitative ou quantitative :

variable qualitative : s_12j vaut 1 si la variable j prend la même valeur pour les individus 1 et 2, et vaut 0 sinon. Par exemple, si 1 et 2 sont tous les deux « grand », alors s_12j vaudra 1. Si 1 est « grand » et 2 « petit », s_12j vaudra 0.
variable quantitative : la différence absolue entre les valeurs des deux variables est tout d’abord calculée, soit |y_1j − y_2j|. Puis l’écart maximum observé sur l’ensemble du fichier est déterminé et noté R_j. Dès lors, la similarité partielle vaut S_12j = 1 - |y_1j − y_2j| / R_j.

Dans le cas où l’on n’a que des variables qualitatives, la valeur de l’indice de Gower correspond à la proportion de caractères en commun. Supposons des individus 1 et 2 décris ainsi :

homme / grand / blond / étudiant / urbain
femme / grande / brune / étudiante / rurale

Sur les 5 variables utilisées pour les décrire, 1 et 2 ont deux caractéristiques communes : ils sont grand(e)s et étudiant(e)s. Dès lors, l’indice de similarité de Gower entre 1 et 2 vaut 2/5 = 0,4 (soit une distance de 1 − 0,4 = 0,6).

Plusieurs approches peuvent être retenues pour traiter les valeurs manquantes :

supprimer tout individu n’étant pas renseigné pour toutes les variables de l’analyse ;
considérer les valeurs manquantes comme une modalité en tant que telle ;
garder les valeurs manquantes en tant que valeurs manquantes.

Le choix retenu modifiera les distances de Gower calculées. Supposons que l’on ait :

homme / grand / blond / étudiant / urbain
femme / grande / brune / étudiante / manquant

Si l’on supprime les individus ayant des valeurs manquantes, 2 est retirée du fichier d’observations et aucune distance n’est calculée.

Si l’on traite les valeurs manquantes comme une modalité particulière, 1 et 2 partagent alors 2 caractères sur les 5 analysés, la distance de Gower entre eux est alors de 1 − 2/5 =1 − 0,4 = 0,6.

Si on garde les valeurs manquantes, l’indice de Gower est dès lors calculé sur les seuls descripteurs renseignés à la fois pour 1 et 2. La distance de Gower sera calculée dans le cas présent uniquement sur les 4 caractères renseignés et vaudra 1 − 2/4 = 0,5.

Distance du Φ²

Il s’agit de la distance utilisée dans les analyses de correspondance multiples (ACM). C’est une variante de la distance du χ². Nous considérons ici que nous avons Q questions (soit Q variables initiales de type facteur). À chaque individu est associé un patron c’est-à-dire une certaine combinaison de réponses aux Q questions. La distance entre deux individus correspond à la distance entre leurs deux patrons. Si les deux individus présentent le même patron, leur distance sera nulle. La distance du Φ² peut s’exprimer ainsi :

$d_{Φ^{2}}^{2} (L_{i}, L_{j}) = \frac{1}{Q} \sum_{k} \frac{{(δ_{i k} - δ_{j k})}^{2}}{f_{k}}$

où L_i et L_j sont deux patrons, Q le nombre total de questions. δ_ik vaut 1 si la modalité k est présente dans le patron L_i, 0 sinon. f_k est la fréquence de la modalité k dans l’ensemble de la population.

Exprimé plus simplement, on fait la somme de l’inverse des modalités non communes aux deux patrons, puis on divise par le nombre total de question. Si nous reprenons notre exemple précédent :

homme / grand / blond / étudiant / urbain
femme / grande / brune / étudiante / rurale

Pour calculer la distance entre 1 et 2, il nous faut connaître la proportion des différentes modalités dans l’ensemble de la population étudiée. En l’occurrence :

hommes : 52 % / femmes : 48 %
grand : 30 % / moyen : 45 % / petit : 25 %
blond : 15 % / châtain : 45 % / brun : 30 % / blanc : 10 %
étudiant : 20 % / salariés : 65 % / retraités : 15 %
urbain : 80 % / rural : 20 %

Les modalités non communes entre les profils de 1 et 2 sont : homme, femme, blond, brun, urbain et rural. La distance du Φ² entre 1 et 2 est donc la suivante :

$d_{Φ^{2}}^{2} (L_{1}, L_{2}) = \frac{1}{5} (\frac{1}{0, 52} + \frac{1}{0, 48} + \frac{1}{0, 15} + \frac{1}{0, 30} + \frac{1}{0, 80} + \frac{1}{0, 20}) = 4, 05$

Cette distance, bien que moins intuitive que la distance de Gower évoquée précédemment, est la plus employée pour l’analyse d’enquêtes en sciences sociales. Il faut retenir que la distance entre deux profils est dépendante de la distribution globale de chaque modalité dans la population étudiée. Ainsi, si l’on recalcule les distances entre individus à partir d’un sous-échantillon, le résultat obtenu sera différent. De manière générale, les individus présentant des caractéristiques rares dans la population vont se retrouver éloignés des individus présentant des caractéristiques fortement représentées.

Exemple

Nous allons reprendre l’ACM calculée avec dudi.acm (ade4) dans le chapitre consacré à l’ACM :

library(questionr)
data(hdv2003)
d <- hdv2003
d$grpage <- cut(d$age, c(16, 25, 45, 65, 93), right = FALSE, include.lowest = TRUE)
d$etud <- d$nivetud
levels(d$etud) <- c(
  "Primaire", "Primaire", "Primaire", "Secondaire", "Secondaire",
  "Technique/Professionnel", "Technique/Professionnel", "Supérieur"
)
d2 <- d[, c("grpage", "sexe", "etud", "peche.chasse", "cinema", "cuisine", "bricol", "sport", "lecture.bd")]
library(ade4)
acm <- dudi.acm(d2, scannf = FALSE, nf = 5)

La matrice des distances s’obtient dès lors avec la fonction dist.dudi :

md <- dist.dudi(acm)

Pour une matrice de distances basée sur la distance de Gower, nous aurions eu plutôt recours à la fonction daisy de l’extension cluster.

library(cluster)
md_gower <- daisy(d2, metric = "gower")

Calcul du dendrogramme

Il faut ensuite choisir une méthode d’agrégation pour construire le dendrogramme. De nombreuses solutions existent (saut minimum, distance maximum, moyenne, Ward…). Chacune d’elle produira un dendrogramme différent. Nous ne détaillerons pas ici ces différentes techniques⁵. Cependant, à l’usage, on privilégiera le plus souvent la méthode de Ward⁶. De manière simplifiée, cette méthode cherche à minimiser l’inertie intra-classe et à maximiser l’inertie inter-classe afin d’obtenir des classes les plus homogènes possibles. Cette méthode est souvent incorrectement présentée comme une méthode de minimisation de la variance alors qu’au sens strict Ward vise l’augmentation mininum de la somme des carrés (“minimum increase of sum-of-squares (of errors)”)⁷.

En raison de la variété des distances possibles et de la variété des techniques d’agrégation, on pourra être amené à réaliser plusieurs dendrogrammes différents sur un même jeu de données jusqu’à obtenir une classification qui fait « sens ».

La fonction de base pour le calcul d’un dendrogramme est hclust en précisant le critère d’agrégation avec method. Dans notre cas, nous allons opter pour la méthode de Ward appliquée au carré des distances (ce qu’on indique avec method = "ward.D2"⁸) :

arbre <- hclust(md, method = "ward.D2")

Le temps de calcul d’un dendrogramme peut être particulièrement important sur un gros fichier de données. L’extension fastcluster permet de réduire significativement le temps de calcul. Il suffit d’installer puis d’appeler cette extension. La fonction hclust sera automatiquement remplacée par cette version optimisée. Elle prends les mêmes paramètres :

library(fastcluster)
arbre <- hclust(md, method = "ward.D2")

Le dendrogramme obtenu peut être affiché simplement avec plot. Lorsque le nombre d’individus est important, il peut être utile de ne pas afficher les étiquettes des individus avec labels=FALSE.

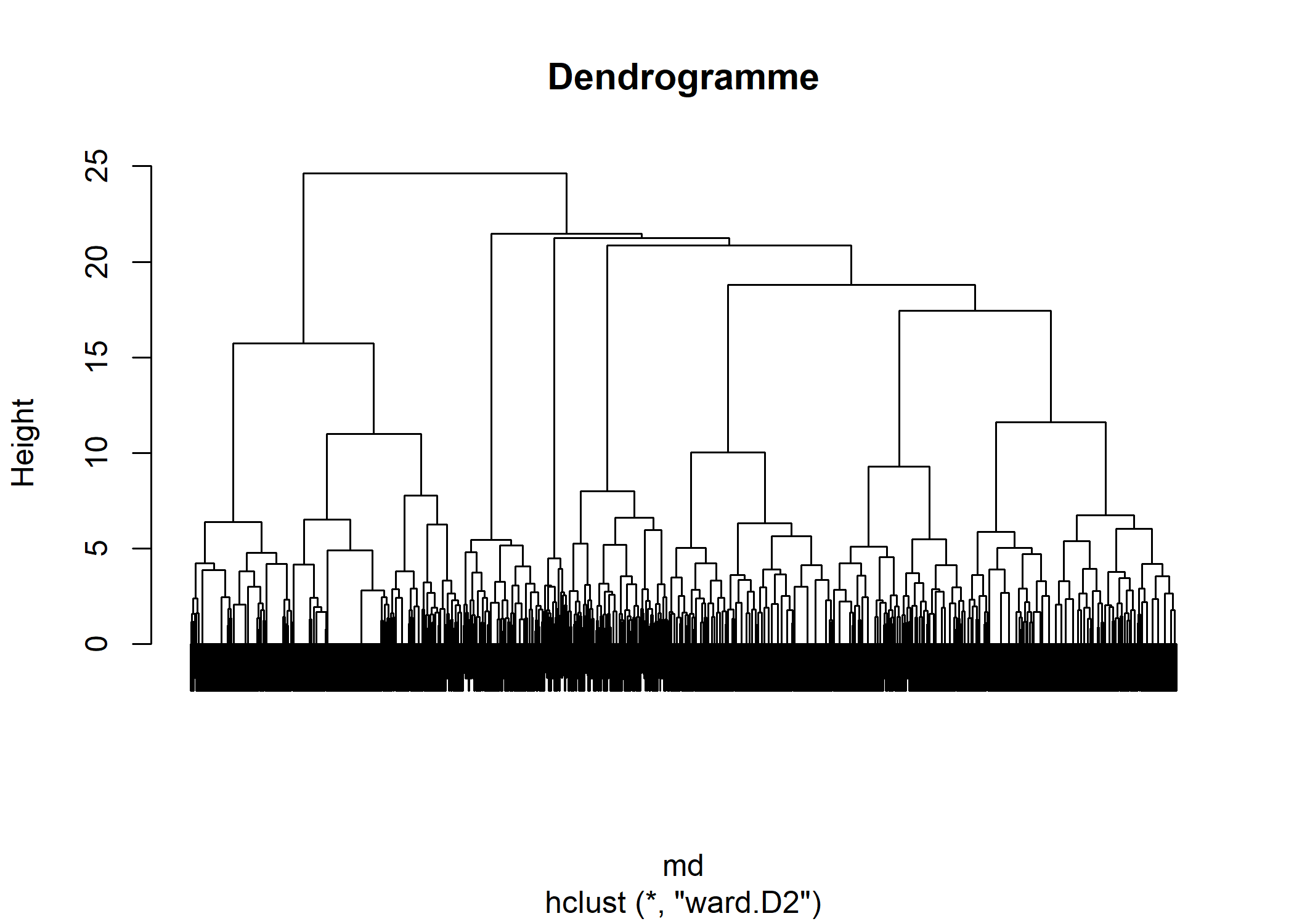
Pour afficher un dendrogramme via ggplot2, on pourra avoir recours à la fonction ggdendrogram de l’extension ggdendro.

La fonction agnes de l’extension cluster peut également être utilisée pour calculer le dendrogramme. Cependant, à l’usage, elle semble être un peu plus lente que hclust.

library(cluster)
arbre2 <- agnes(md, method = "ward")

ATTENTION : la méthode implémentée dans la fonction agnes correspond à l’option method = "ward.D2" de hclust.

Le résultat obtenu n’est pas au même format que celui de hclust. Il est possible de transformer un objet agnes au format hclust avec as.hclust.

as.hclust(arbre2)

Découper le dendrogramme

Pour obtenir une partition de la population, il suffit de découper le dendrogramme obtenu à une certaine hauteur. En premier lieu, une analyse de la forme du dendrogramme pourra nous donner une indication sur le nombre de classes à retenir. Dans notre exemple, deux branches bien distinctes apparaissent sur l’arbre.

Pour nous aider, nous pouvons représenter les sauts d’inertie du dendrogramme selon le nombre de classes retenues.

On voit trois sauts assez nets à 2, 5 et 8 classes, que nous avons représentés ci-dessous respectivement en vert, en rouge et en bleu.

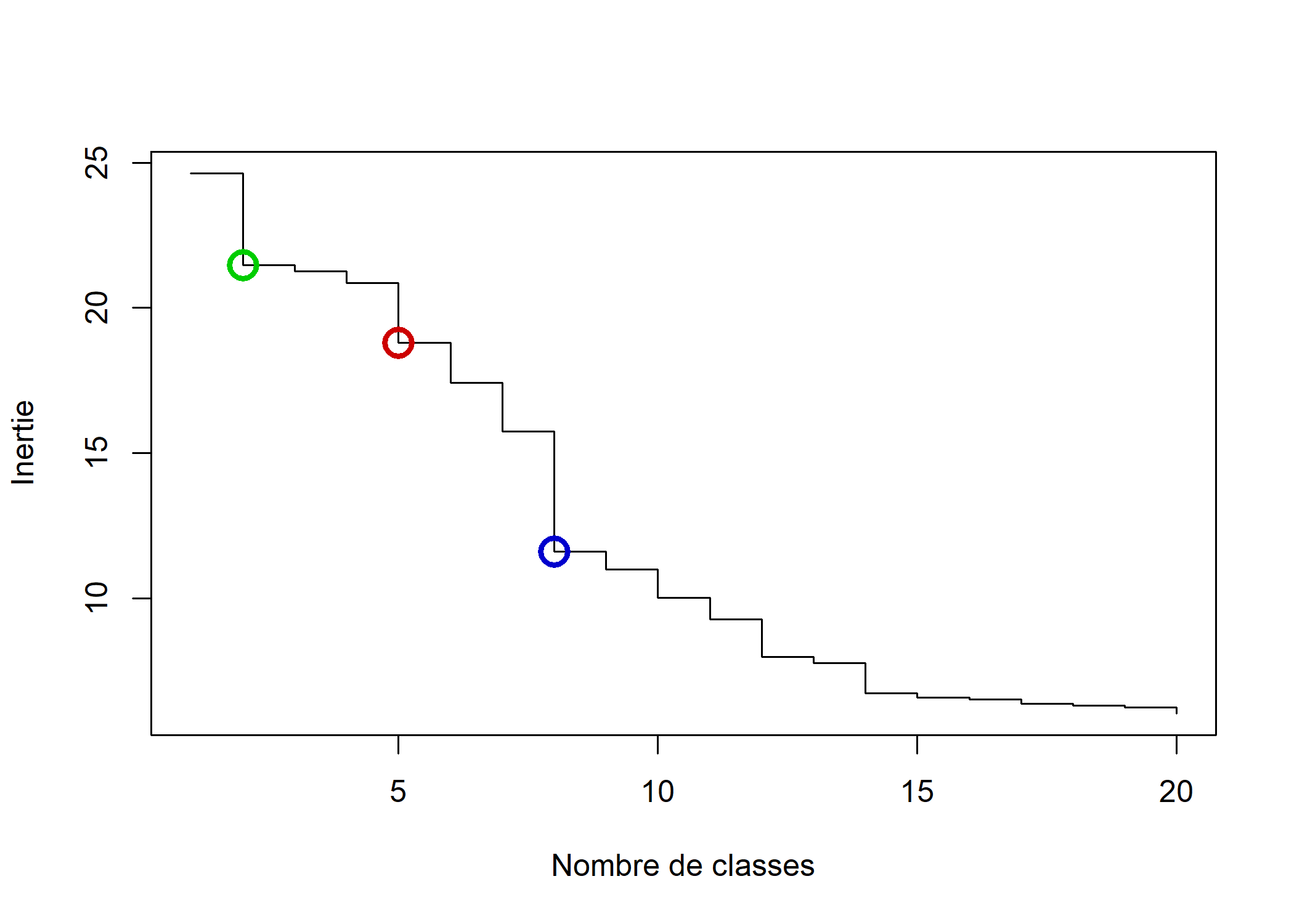
La fonction rect.hclust permet de visualiser les différentes partitions directement sur le dendrogramme.

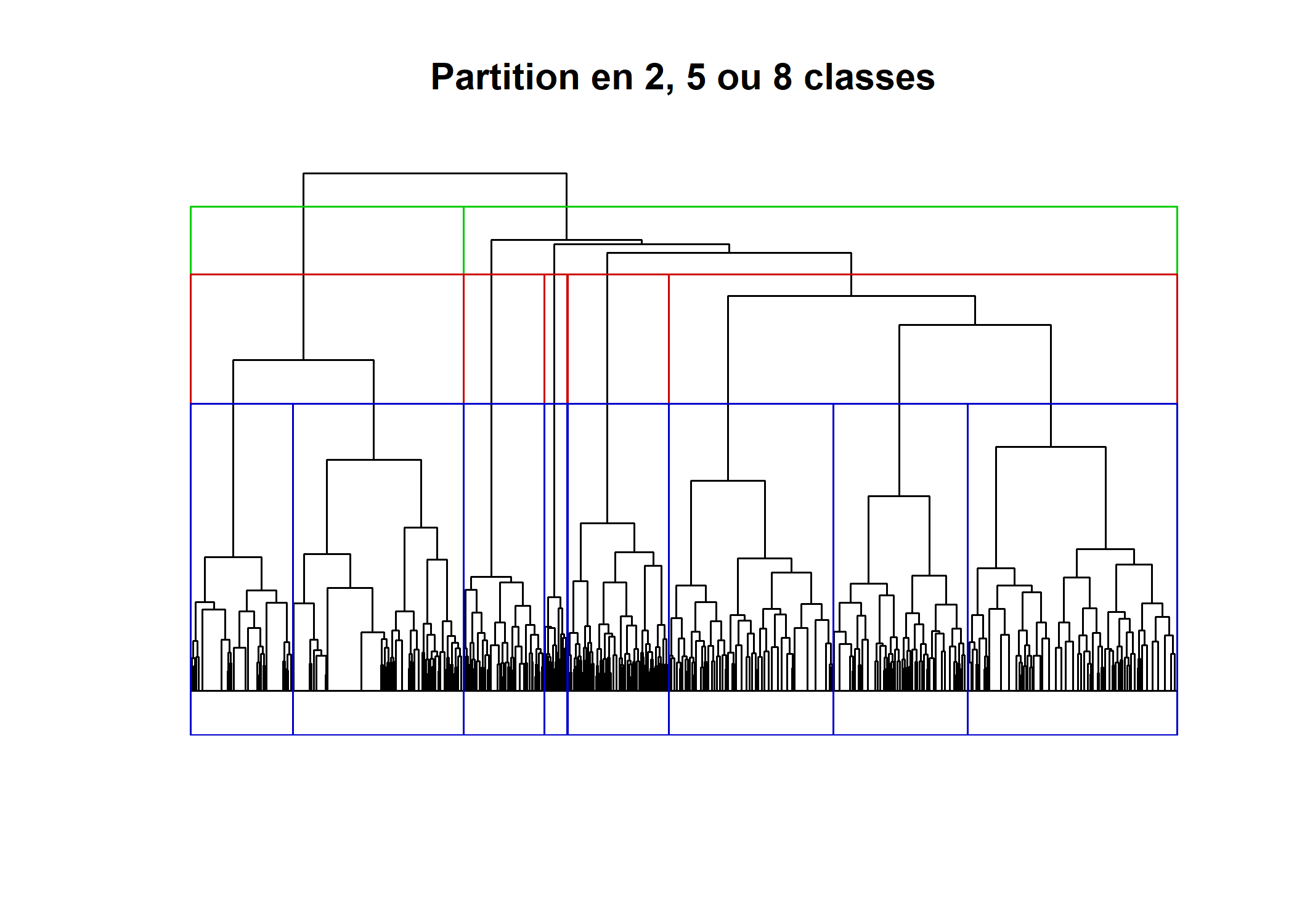
On peut également avoir recours à l’extension dendextend et sa fonction color_branches. À noter que dendextend fournit une méthode permettant de passer un dendrogramme à ggplot.

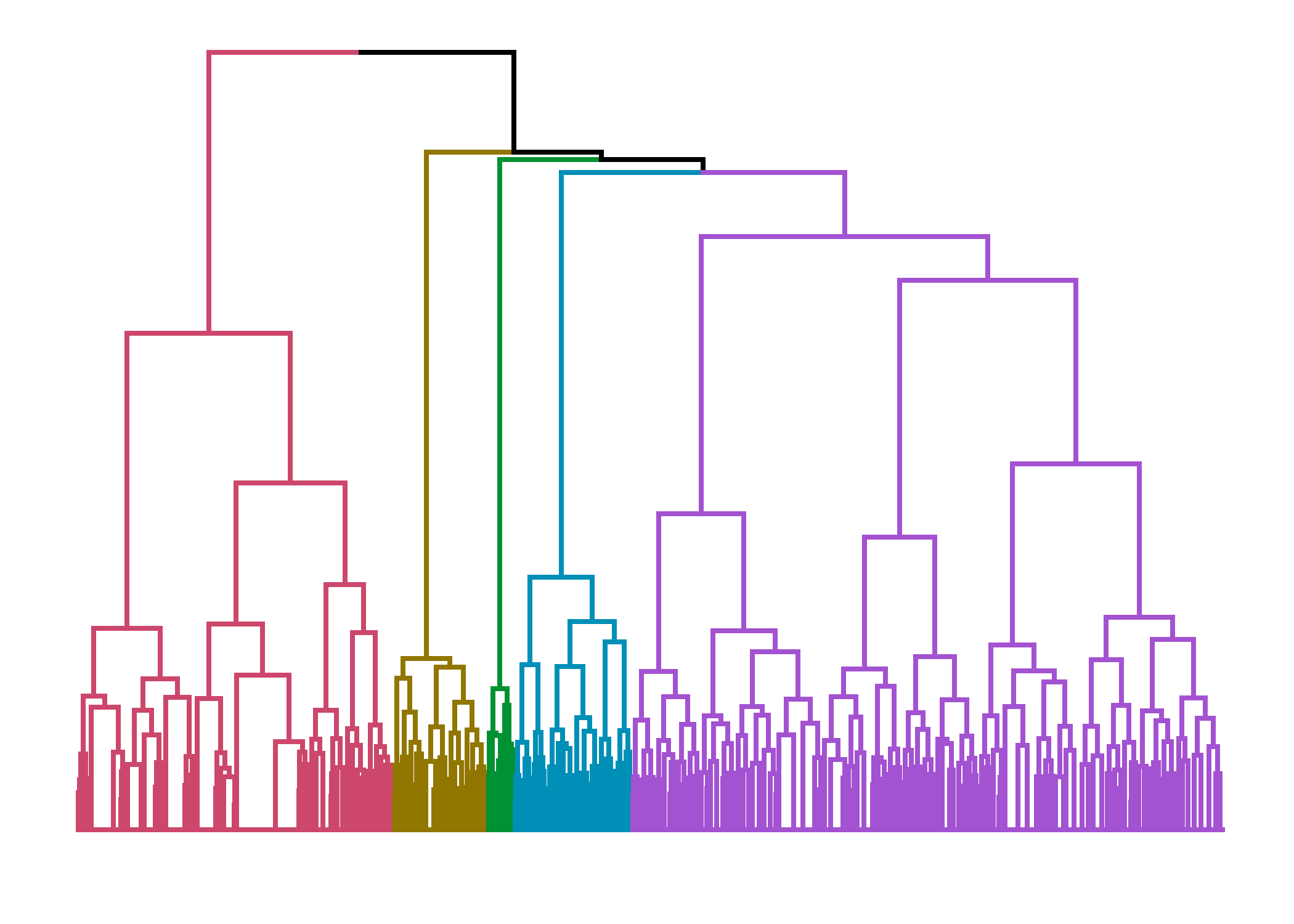
On peut aussi avoir recours à la fonction fviz_dend de l’extension factoextra.

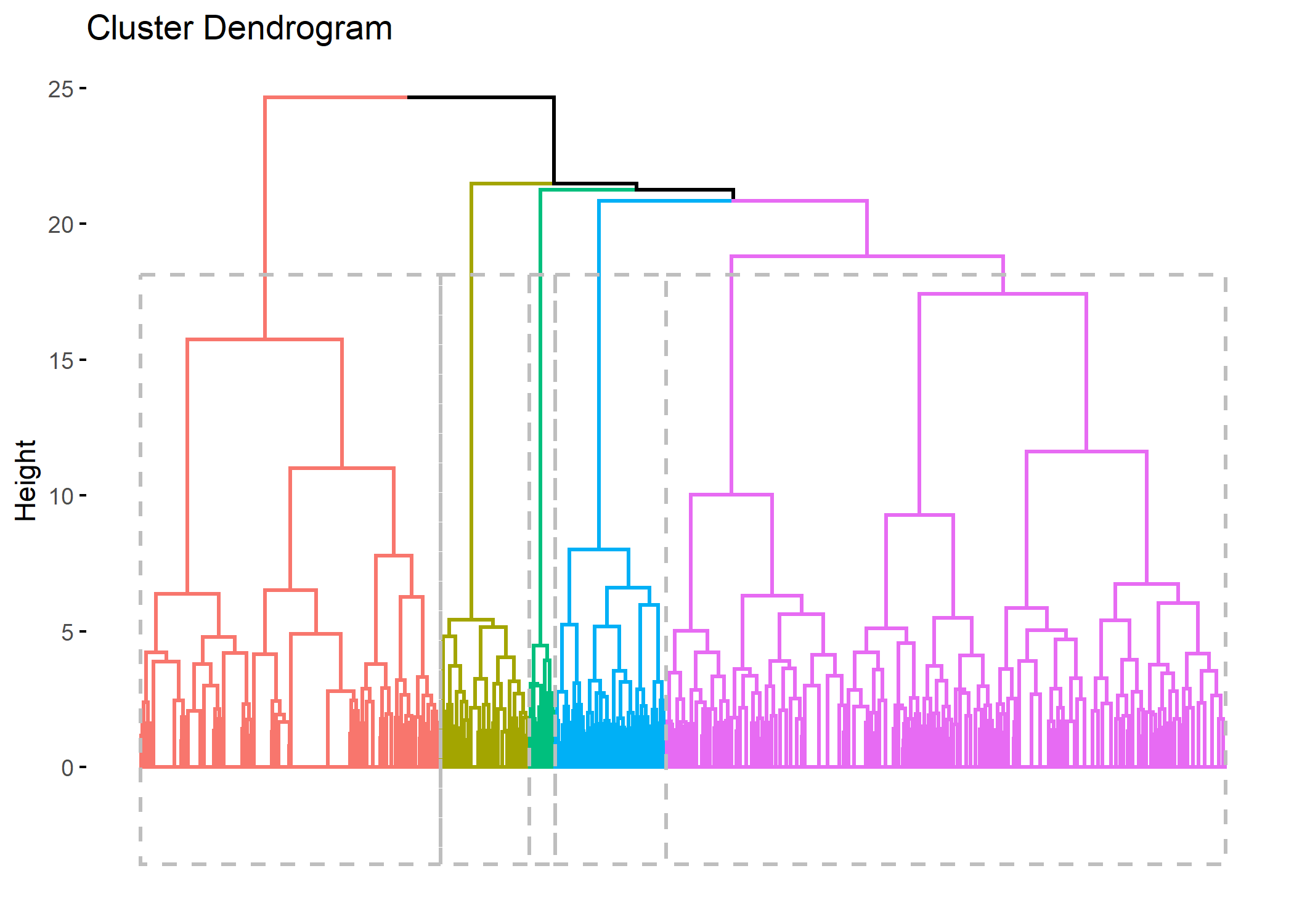
L’extension FactoMineR (que nous aborderons dans une section dédiée ci-après) suggère d’utiliser la partition ayant la plus grande perte relative d’inertie.

L’extension JLutils (disponible sur GitHub) propose une fonction best.cutree qui permet de calculer cette indicateur à partir de n’importe quel dendrogramme calculé avec hclust ou agnes.

Pour installer JLutils, on aura recours au package devtools et à sa fonction install_github :

library(devtools)
install_github("larmarange/JLutils")

Pour installer JLutils sur un PC sous Windows, vous aurez également besoin de Rtools, téléchargeable sur https://cran.r-project.org/bin/windows/Rtools/. Une fois installée, pensez à charger l’extension.

library(JLutils)

Si vous rencontrez des difficultés avec l’installation de JLutils et si vous avez seulement besoin de best.cutree, vous pouvez avoir recours à la commande suivante.

source(url("https://raw.githubusercontent.com/larmarange/JLutils/master/R/clustering.R"))

Par défaut, best.cutree regarde quelle serait la meilleure partition entre 3 et 20 classes.

best.cutree(arbre)

[1] 5

En l’occurence il s’agirait d’une partition en 5 classes. Il est possible de modifier le minimum et le maximum des partitions recherchées avec min et max.

best.cutree(arbre, min = 2)

[1] 2

On peut également représenter le graphique des pertes relatives d’inertie avec graph=TRUE. La meilleure partition selon ce critère est représentée par un point noir et la seconde par un point gris.

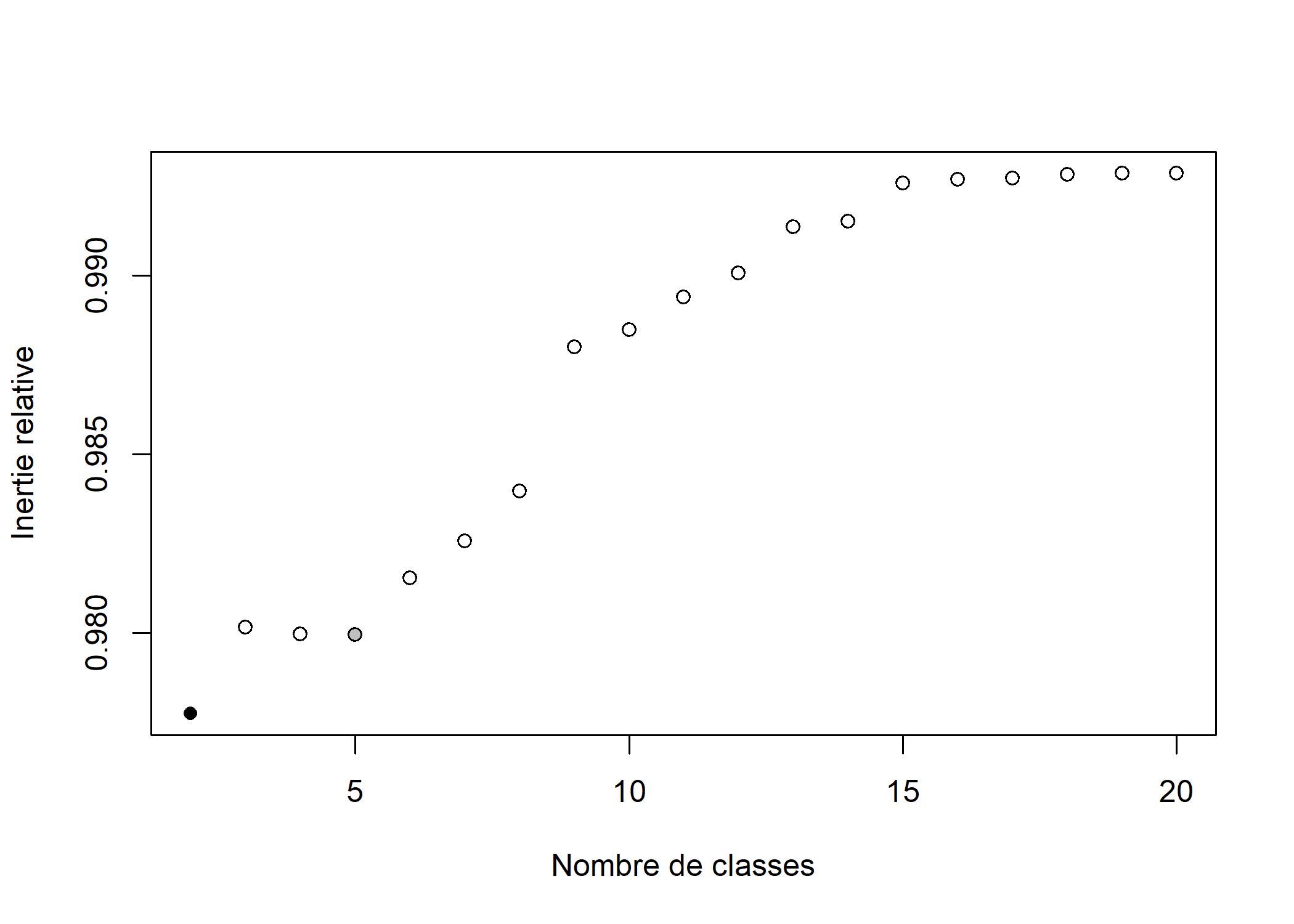
Perte relative d’inertie selon le nombre de classes

Un découpage en deux classes minimise ce critère. Cependant, si l’on souhaite réaliser une analyse un peu plus fine, un nombre de classes plus élevé serait pertinent. Nous allons donc retenir un découpage en cinq classes. Le découpage s’effectue avec la fonction cutree.

typo <- cutree(arbre, 5)
freq(typo)

Je peux ajouter directement ma typologie à mon objet d2 ou même d dans la mesure où je n’ai pas modifié depuis le début du script l’ordre de mes observations. Dès lors, l’ordre du résultat renvoyé par cutree correspond à l’ordre de ma matrice de distance qui elle-même est ordonnée selon les observations de l’ACM qui est ordonnée selon l’ordre des observations du tableau de données initial.

d2$typo <- cutree(arbre, 5)

Il existe de multiples autres indicateurs statistiques cherchant à mesurer la qualité de chaque partition. Pour cela, on pourra par exemple avoir recours à la fonction as.clustrange de l’extension WeightedCluster.

Pour plus d’informations, voir le manuel de la librairie WeightedCluster, chapitre 7.

library(WeightedCluster)

This is WeightedCluster stable version 1.6-0 (Built: 2023-01-10)


To get the manuals, please run:

   vignette("WeightedCluster") ## Complete manual in English

   vignette("WeightedClusterFR") ## Complete manual in French

   vignette("WeightedClusterPreview") ## Short preview in English


To cite WeightedCluster in publications please use:

Studer, Matthias (2013). WeightedCluster Library

   Manual: A practical guide to creating typologies

   of trajectories in the social sciences with R.

   LIVES Working Papers, 24. doi:

   10.12682/lives.2296-1658.2013.24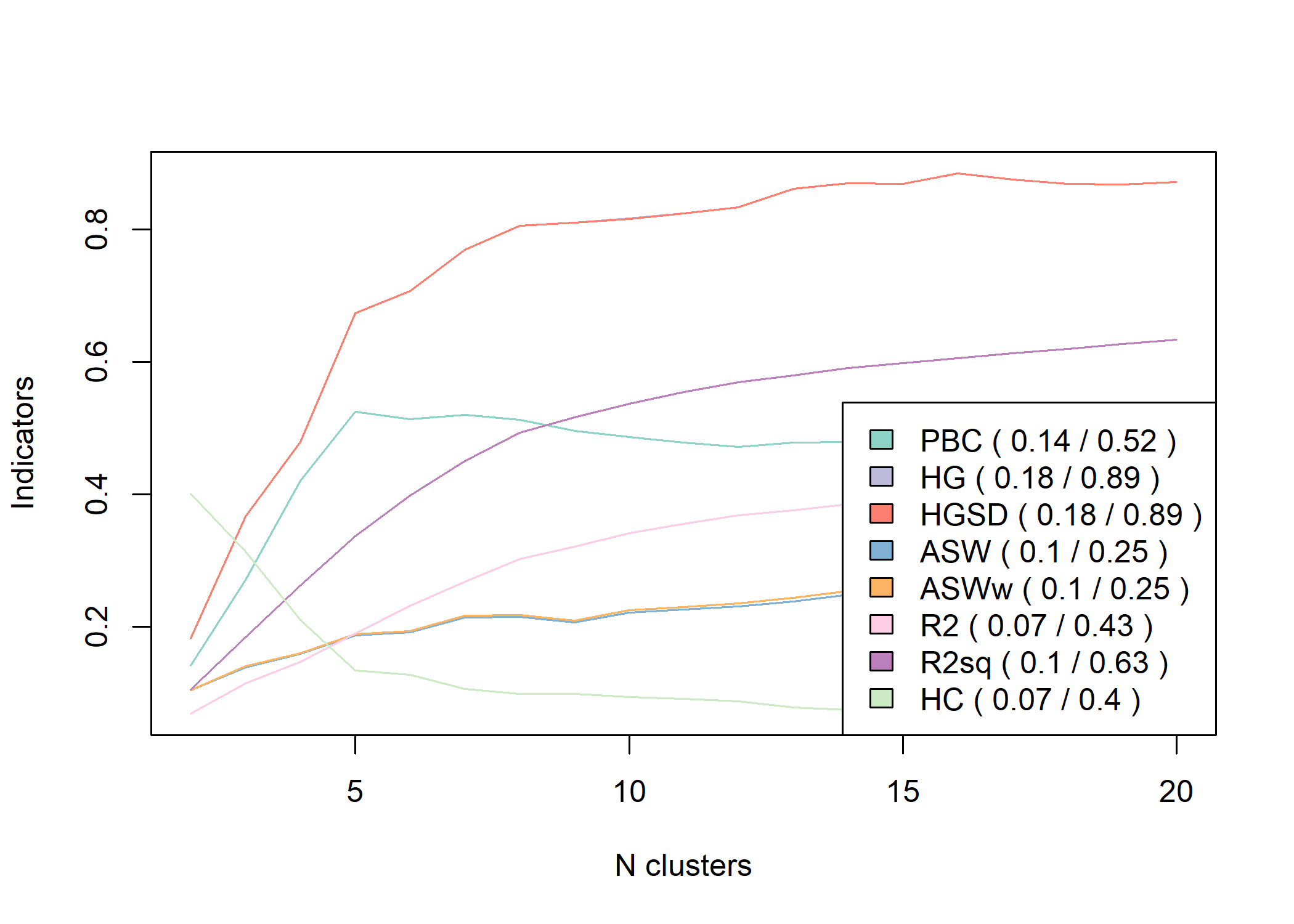

plot(as.clustrange(arbre, md))

La typologie obtenue peut être représentée dans le plan factoriel avec s.class.

Projection de la typologie obtenue par CAH selon les 4 premiers axes

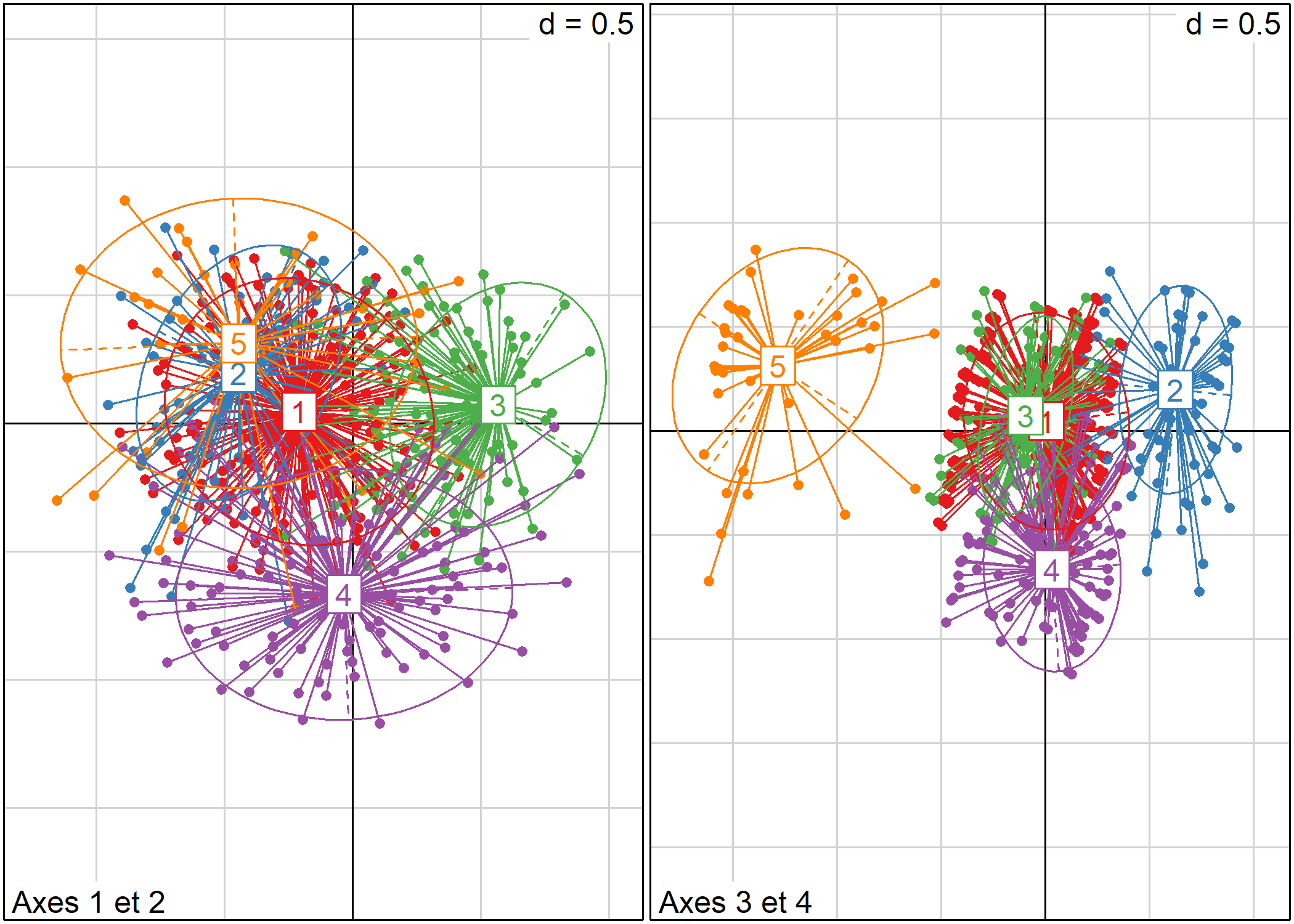
De nombreuses possibilités graphiques sont possibles avec les dendrogrammes. Des exemples documentés sont disponibles à cette adresse : http://rpubs.com/gaston/dendrograms.

Romain François a developpé une fonction A2Rplot permettant de réaliser facilement un dendrogramme avec les branches colorées⁹. Par commodité, cette fonction est disponible directement au sein de l’extension JLutils.

Si vous rencontrez des difficultés à installer JLutils, vous pouvez également charger seulement A2Rplotsource() avec la commande :

source(url("https://raw.githubusercontent.com/larmarange/JLutils/master/R/A2Rplot.R"))

Pour réaliser le graphique, on indiquera le nombre de classes et les couleurs à utiliser pour chaque branche de l’arbre :

A2Rplot(arbre, k = 5, boxes = FALSE, col.up = "gray50", col.down = brewer.pal(5, "Dark2"), show.labels = FALSE)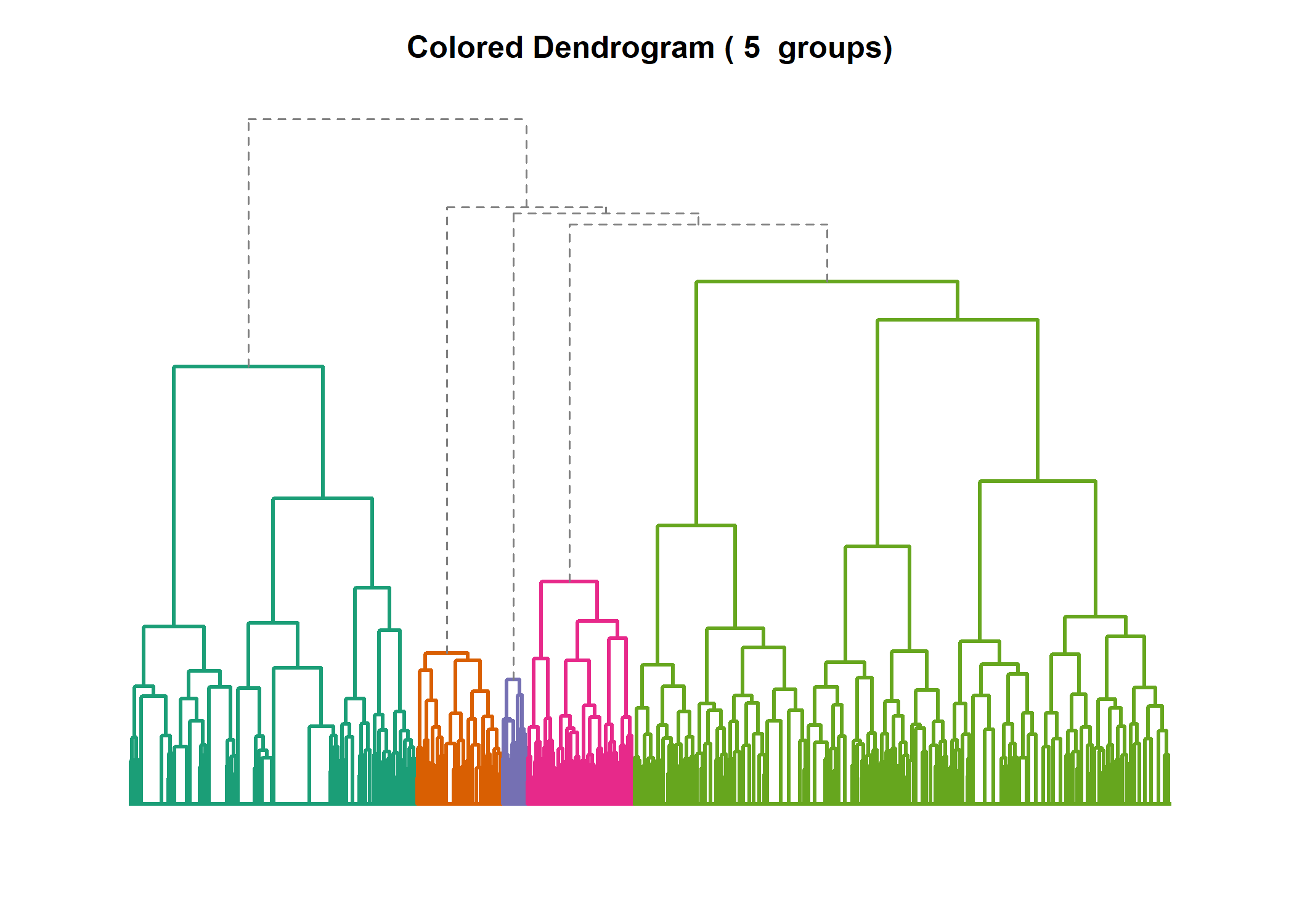

Pour plus d’options graphiques concernant les dendrogrammes en général, on pourra se référer à l’extension dendextend : https://talgalili.github.io/dendextend/.

Caractériser la typologie

Reste le travail le plus important (et parfois le plus difficile) qui consiste à catégoriser la typologie obtenue et le cas échéant à nommer les classes.

En premier lieu, on peut croiser la typologie obtenue avec les différentes variables inclues dans l’ACM. Le plus simple est d’avoir recours à tbl_summary de gtsummary.

library(gtsummary)
d2 %>%
  tbl_summary(by = typo)

Characteristic	1, N = 1,031¹	2, N = 164¹	3, N = 553¹	4, N = 205¹	5, N = 47¹
grpage
[16,25)	0 (0%)	164 (100%)	0 (0%)	0 (0%)	5 (11%)
[25,45)	590 (57%)	0 (0%)	20 (3.6%)	80 (39%)	16 (34%)
[45,65)	441 (43%)	0 (0%)	185 (34%)	97 (47%)	22 (47%)
[65,93]	0 (0%)	0 (0%)	346 (63%)	28 (14%)	4 (8.5%)
Unknown	0	0	2	0	0
sexe
Homme	429 (42%)	74 (45%)	220 (40%)	161 (79%)	15 (32%)
Femme	602 (58%)	90 (55%)	333 (60%)	44 (21%)	32 (68%)
etud
Primaire	7 (0.7%)	1 (1.3%)	402 (73%)	50 (25%)	6 (14%)
Secondaire	267 (26%)	15 (19%)	65 (12%)	35 (17%)	5 (12%)
Technique/Professionnel	406 (40%)	48 (62%)	48 (8.7%)	87 (43%)	5 (12%)
Supérieur	334 (33%)	14 (18%)	36 (6.5%)	30 (15%)	27 (63%)
Unknown	17	86	2	3	4
peche.chasse
Non	1,030 (100%)	151 (92%)	553 (100%)	0 (0%)	42 (89%)
Oui	1 (<0.1%)	13 (7.9%)	0 (0%)	205 (100%)	5 (11%)
cinema
Non	497 (48%)	32 (20%)	486 (88%)	141 (69%)	18 (38%)
Oui	534 (52%)	132 (80%)	67 (12%)	64 (31%)	29 (62%)
cuisine
Non	539 (52%)	85 (52%)	361 (65%)	111 (54%)	23 (49%)
Oui	492 (48%)	79 (48%)	192 (35%)	94 (46%)	24 (51%)
bricol
Non	537 (52%)	103 (63%)	397 (72%)	89 (43%)	21 (45%)
Oui	494 (48%)	61 (37%)	156 (28%)	116 (57%)	26 (55%)
sport
Non	588 (57%)	57 (35%)	479 (87%)	130 (63%)	23 (49%)
Oui	443 (43%)	107 (65%)	74 (13%)	75 (37%)	24 (51%)
lecture.bd
Non	1,031 (100%)	164 (100%)	553 (100%)	205 (100%)	0 (0%)
Oui	0 (0%)	0 (0%)	0 (0%)	0 (0%)	47 (100%)
¹ n (%)

On peut également avoir recours à ggtable de GGally pour représenter les résidus du Chi² et mieux repérer les différences.

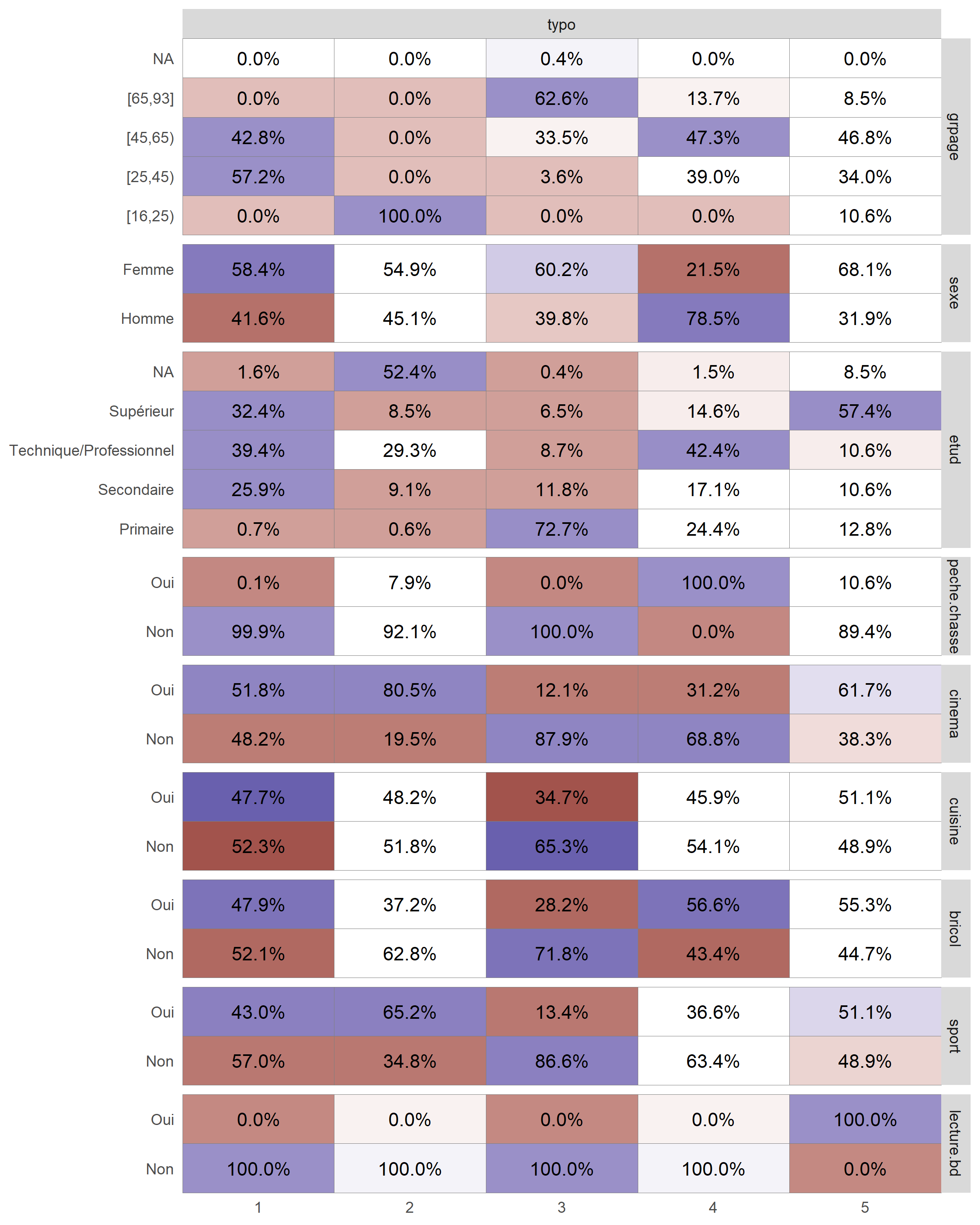
CAH avec l’extension FactoMineR

L’extension FactoMineR fournit une fonction HCPC permettant de réaliser une classification hiérarchique à partir du résultats d’une analyse factorielle réalisée avec la même extension (voir la section dédiée du chapitre sur l’ACM).

HCPC réalise à la fois le calcul de la matrice des distances, du dendrogramme et le partitionnement de la population en classes. Par défaut, HCPC calcule le dendrogramme à partir du carré des distances du Φ² et avec la méthode de Ward.

Par défaut, l’arbre est affiché à l’écran et l’arbre sera coupé selon la partition ayant la plus grande perte relative d’inertie (comme avec best.cutree). Utilisez graph=FALSE pour ne pas afficher le graphique et l’argument nb.clust pour indiquer le nombre de classes désirées.

library(FactoMineR)
acm2 <- MCA(d2[complete.cases(d2), ], ncp = 5, graph = FALSE)
cah <- HCPC(acm2, graph = FALSE)

On pourra représenter le dendrogramme avec plot et l’argument choice="tree".

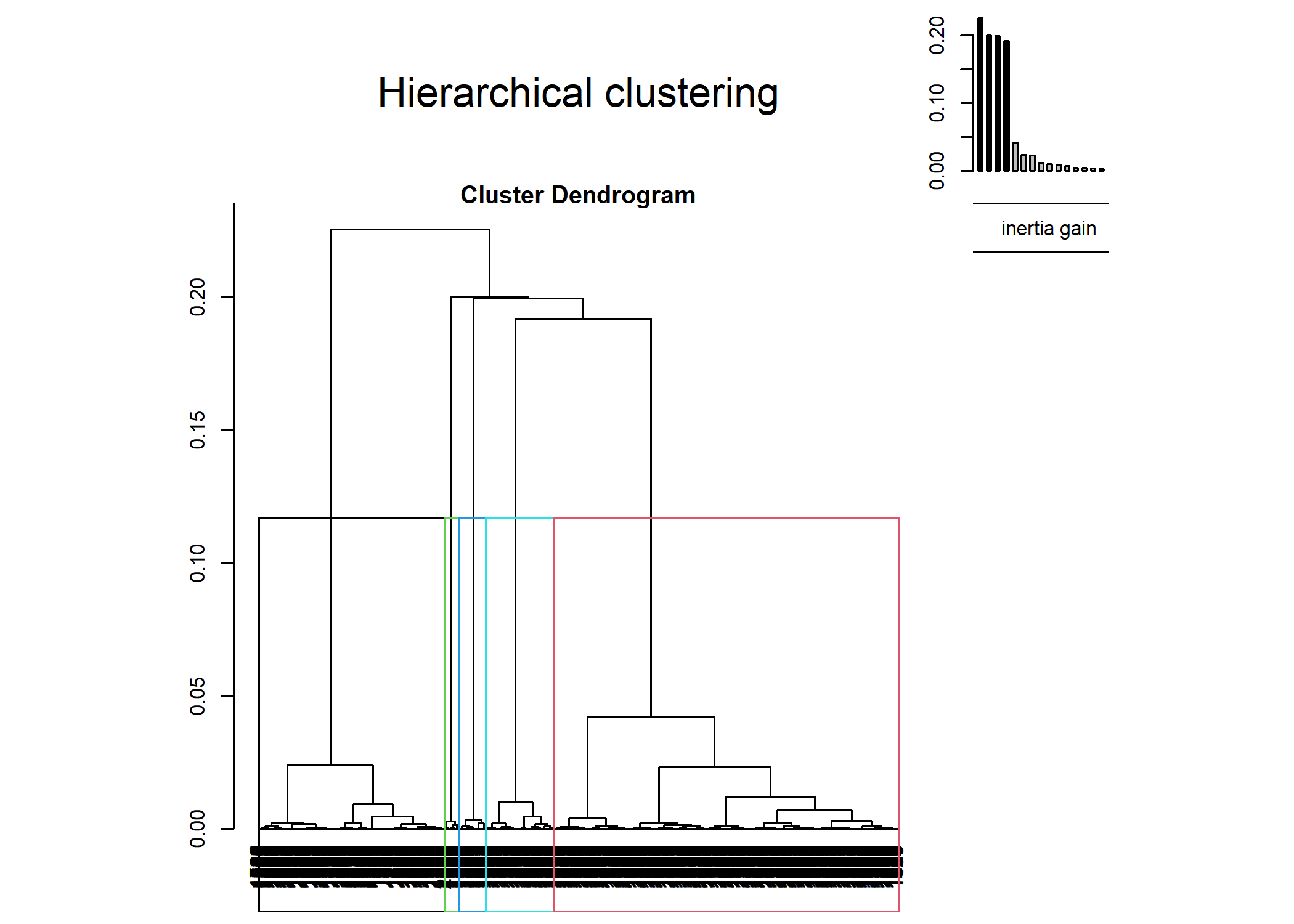
Il apparait que le dendrogramme obtenu avec HCPC diffère de celui que nous avons calculé précédemment en utilisant la matrice des distances fournies par dist.dudi. Cela est dû au fait que HCPC procède différement pour calculer la matrice des distances en ne prenant en compte que les axes retenus dans le cadre de l’ACM. Pour rappel, nous avions retenu que 5 axes dans le cadre de notre ACM :

acm2 <- MCA(d2[complete.cases(d2), ], ncp = 5, graph = FALSE)

HCPC n’a donc pris en compte que ces 5 premiers axes pour calculer les distances entre les individus, considérant que les autres axes n’apportent que du « bruit » rendant la classification instable. Cependant, comme le montre summary(acm2), nos cinq premiers axes n’expliquent que 54 % de la variance. Il usuellement préférable de garder un plus grande nombre d’axes afin de couvrir au moins 80 à 90 % de la variance¹⁰. De son côté, dist.dudi prends en compte l’ensemble des axes pour calculer la matrice des distances. On peut reproduire cela avec FactoMineR en indiquant ncp=Inf lors du calcul de l’ACM.

acm2 <- MCA(d2[complete.cases(d2), ], ncp = Inf, graph = FALSE)
cah <- HCPC(acm2, nb.clust = -1, graph = FALSE)

On obtient bien cette fois-ci le même résultat.

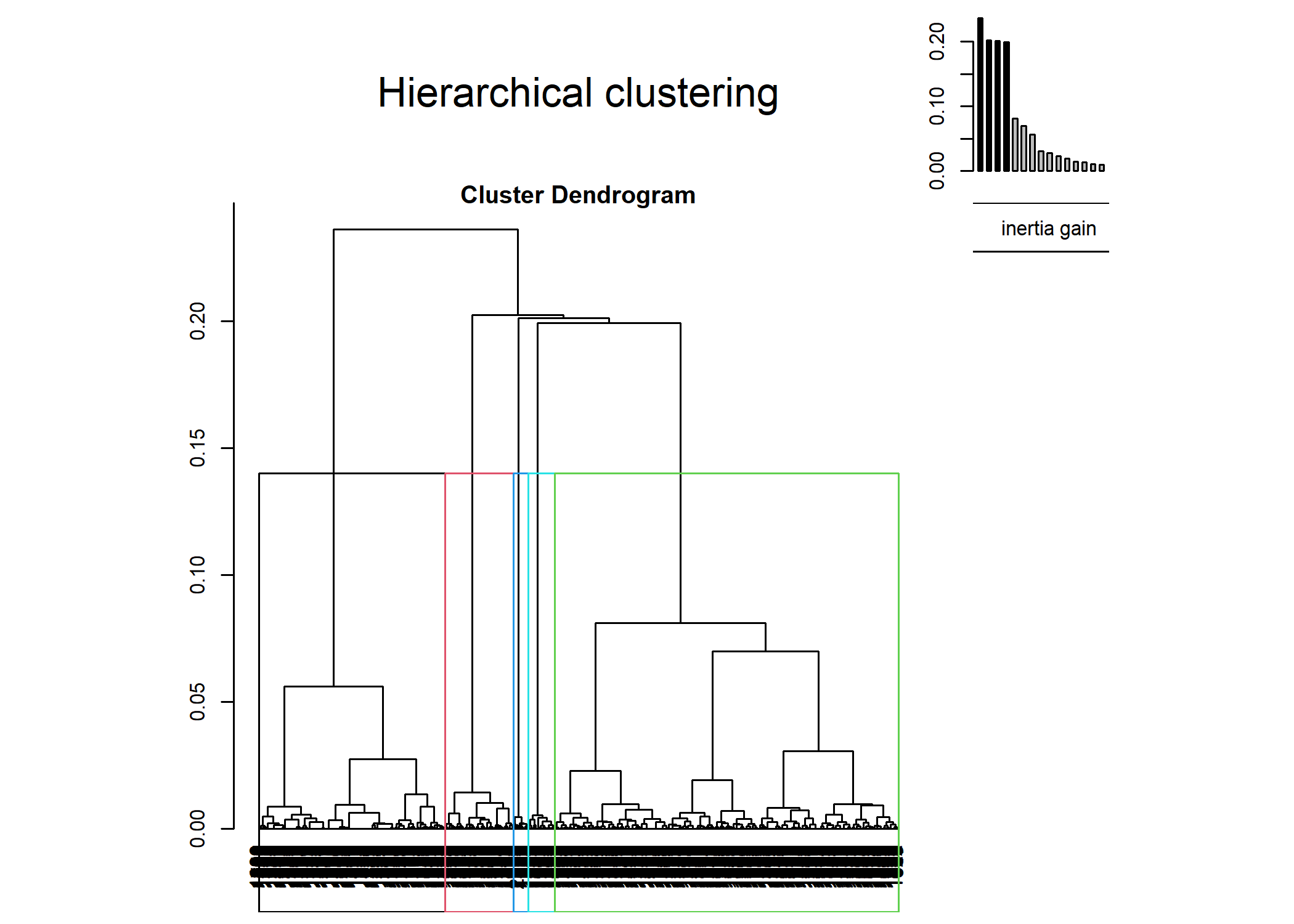
Dendrogramme obtenu avec HCPC (tous les axes)

D’autres graphiques sont disponibles, en faisant varier la valeur de l’argument choice :

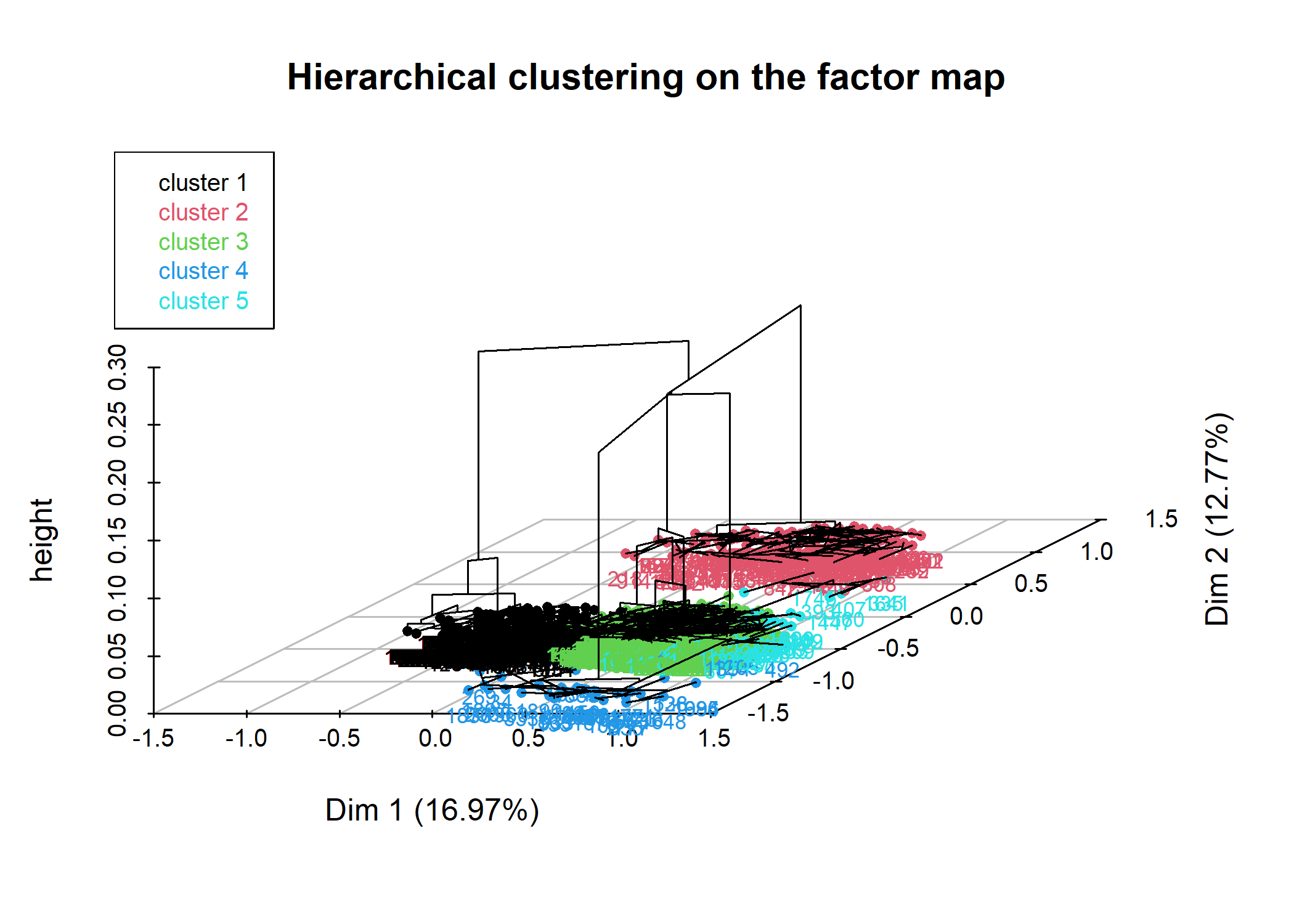
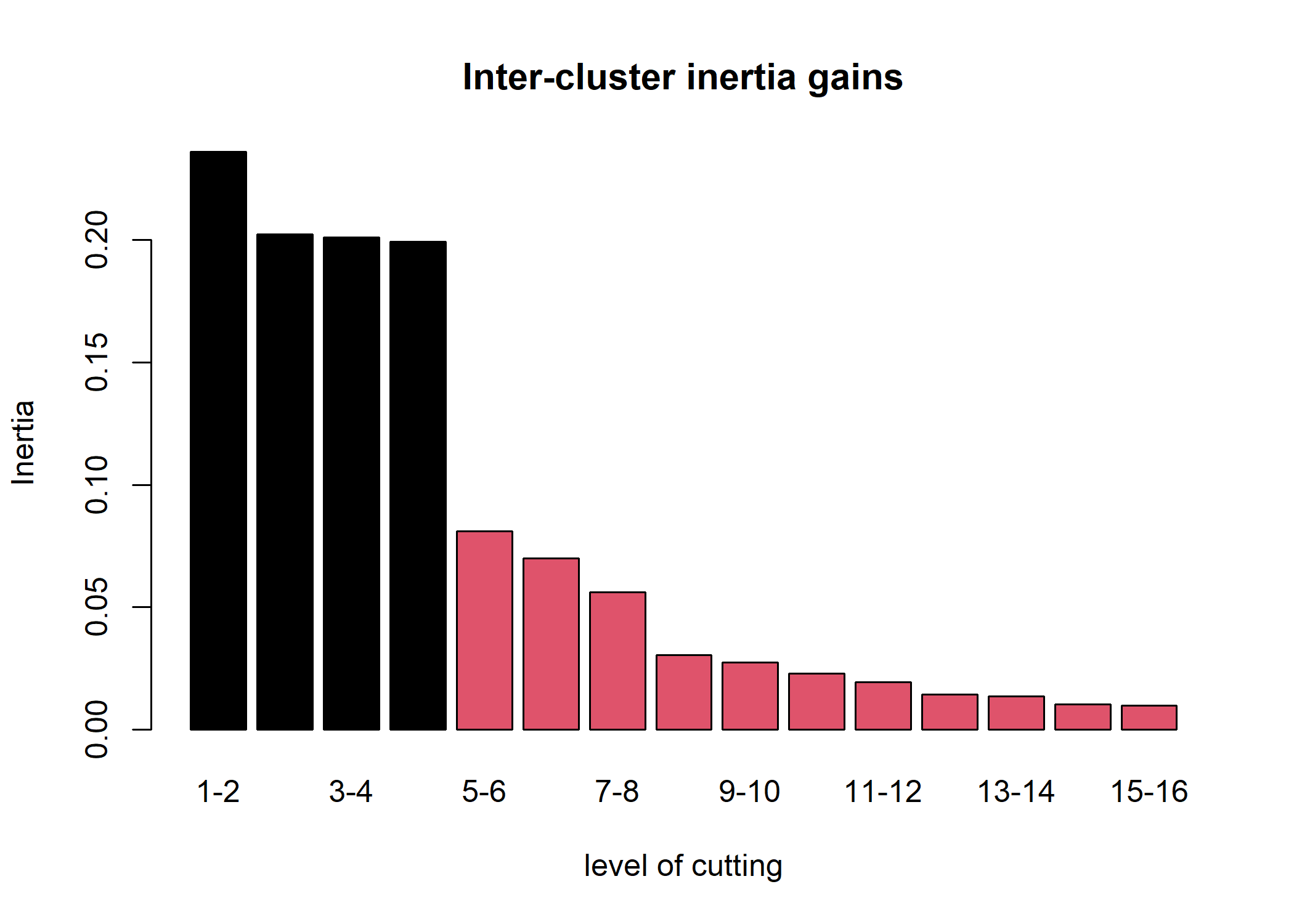
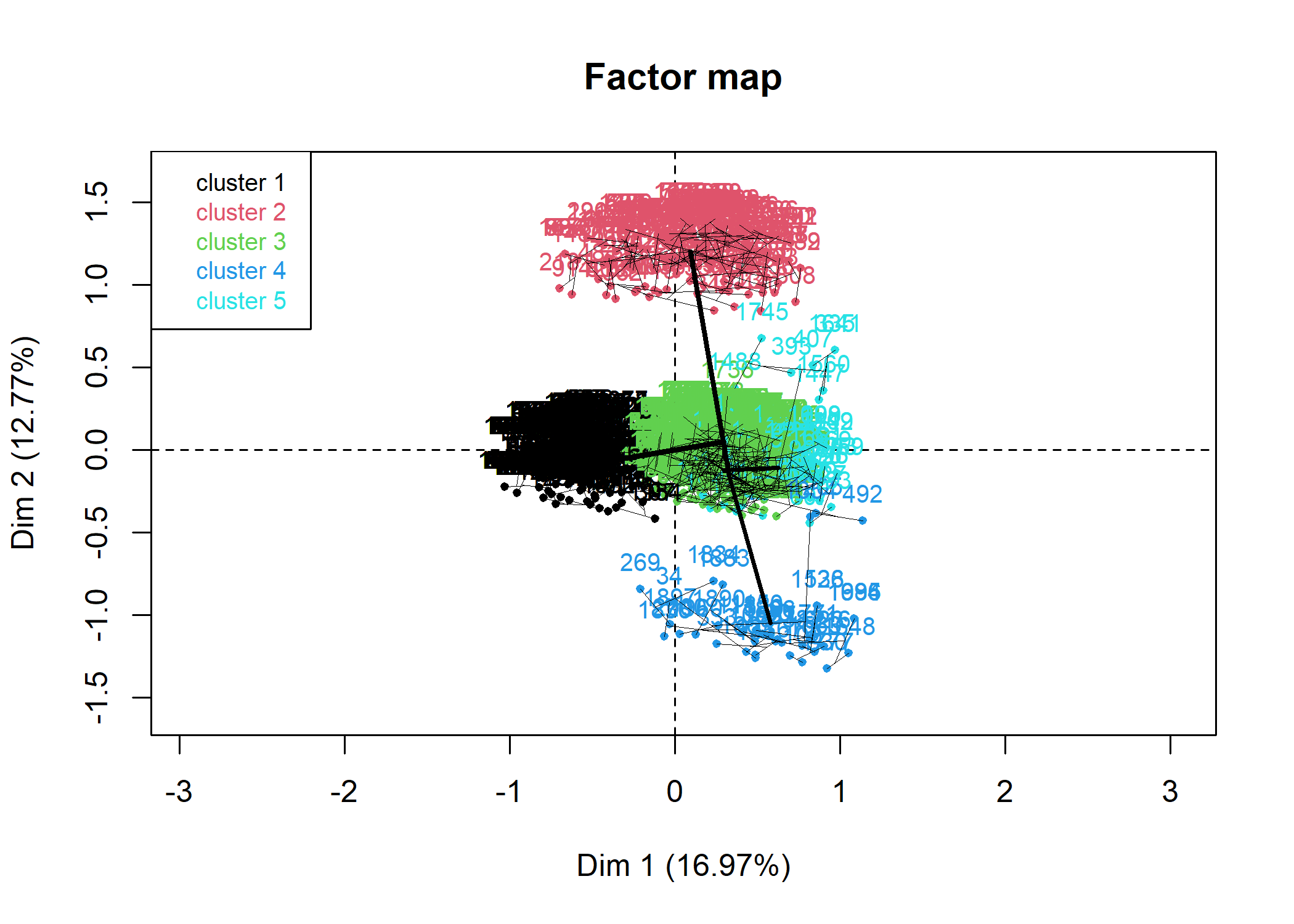
Représentation en 3 dimensions du dendrogramme

Projection des catégories sur le plan factoriel

L’objet renvoyé par HCPC contient de nombreuses informations. La partition peut notamment être récupérée avec cah$data.clust$clust. Il y a également diverses statistiques pour décrire les catégories.

cah

**Results for the Hierarchical Clustering on Principal Components**
   name                   
1  "$data.clust"          
2  "$desc.var"            
3  "$desc.var$test.chi2"  
4  "$desc.axes$category"  
5  "$desc.axes"           
6  "$desc.axes$quanti.var"
7  "$desc.axes$quanti"    
8  "$desc.ind"            
9  "$desc.ind$para"       
10 "$desc.ind$dist"       
11 "$call"                
12 "$call$t"              
   description                                              
1  "dataset with the cluster of the individuals"            
2  "description of the clusters by the variables"           
3  "description of the cluster var. by the categorical var."
4  "description of the clusters by the categories."         
5  "description of the clusters by the dimensions"          
6  "description of the cluster var. by the axes"            
7  "description of the clusters by the axes"                
8  "description of the clusters by the individuals"         
9  "parangons of each clusters"                             
10 "specific individuals"                                   
11 "summary statistics"                                     
12 "description of the tree"

freq(cah$data.clust$clust)

Pour une présentation de ces différentes distances, on pourra se référer à http://old.biodiversite.wallonie.be/outils/methodo/similarite_distance.htm ou encore à ce support de cours par D. Chessel, J. Thioulouse et A.B. Dufour disponible à http://pbil.univ-lyon1.fr/R/pdf/stage7.pdf.↩︎
Cette même fonction peut aussi être utilisée pour calculer une distance après une analyse en composantes principales ou une analyse mixte de Hill et Smith.↩︎
Voir Gower, J. (1971). A General Coefficient of Similarity and Some of Its Properties. Biometrics, 27(4), 857-871. doi:10.2307/2528823 (http://www.jstor.org/stable/2528823).↩︎
Pour une description mathématique plus détaillée de cette fonction, notamment en cas de valeur manquante, se référer à l’article original de Gower précédemment cité.↩︎
On pourra consulter le cours de FG Carpentier déjà cité ou bien des ouvrages d’analyse statistique.↩︎
Ward, J. (1963). Hierarchical Grouping to Optimize an Objective Function. Journal of the American Statistical Association, 58(301), 236-244. doi:10.2307/2282967. (http://www.jstor.org/stable/2282967)↩︎
Voir par exemple la discussion, en anglais, sur Wikipedia concernant la page présentant la méthode Ward : https://en.wikipedia.org/wiki/Talk:Ward%27s_method ↩︎
Depuis la version 3.1 de R. L’option method = "ward.D" correspondant à la version disponible dans les versions précédentes de R. Mais il est à noter que la méthode décrite par Ward dans son article de 1963 correspond en réalité à method = "ward.D2.↩︎
Voir http://addicted2or.free.fr/packages/A2R/lastVersion/R/code.R.↩︎
Voir http://factominer.free.fr/classical-methods/classification-hierarchique-sur-composantes-principales.html ↩︎