Analyse de séquences
Ce chapitre est évoqué dans le webin-R #16 (analyse de séquences) sur YouTube.
Ce chapitre est évoqué dans le webin-R #19 (trajectoires de soins : un exemple de données longitudinales 3 : analyse de séquences) sur YouTube.
La version originale de ce chapitre est une reprise, avec l’aimable autorisation de son auteur, d’un article de Nicolas Robette intitulé L’analyse de séquences : une introduction avec le logiciel R et le package TraMineR et publié sur le blog Quanti (http://quanti.hypotheses.org/686/).
Depuis les années 1980, l’étude quantitative des trajectoires biographiques (life course analysis) a pris une ampleur considérable dans le champ des sciences sociales. Les collectes de données micro-individuelles longitudinales se sont développées, principalement sous la forme de panels ou d’enquêtes rétrospectives. Parallèlement à cette multiplication des données disponibles, la méthodologie statistique a connu de profondes évolutions. L’analyse des biographies (event history analysis) — qui ajoute une dimension diachronique aux modèles économétriques mainstream — s’est rapidement imposée comme l’approche dominante : il s’agit de modéliser la durée des situations ou le risque d’occurrence des événements.
L’analyse de séquences
Cependant, ces dernières années ont vu la diffusion d’un large corpus de méthodes descriptives d’analyse de séquences, au sein desquelles l’appariement optimal (optimal matching) occupe une place centrale1. L’objectif principal de ces méthodes est d’identifier — dans la diversité d’un corpus de séquences constituées de séries d’états successifs — les régularités, les ressemblances, puis le plus souvent de construire des typologies de « séquences-types ». L’analyse de séquences constitue donc un moyen de décrire mais aussi de mieux comprendre le déroulement de divers processus.
La majeure partie des applications de l’analyse de séquences traite de trajectoires biographiques ou de carrières professionnelles. Dans ces cas, chaque trajectoire ou chaque carrière est décrite par une séquence, autrement dit par une suite chronologiquement ordonnée de « moments » élémentaires, chaque moment correspondant à un « état » déterminé de la trajectoire (par exemple, pour les carrières professionnelles : être en emploi, au chômage ou en inactivité). Mais on peut bien sûr imaginer des types de séquences plus originaux : Andrew Abbott2, le sociologue américain qui a introduit l’optimal matching dans les sciences scientifiques ou des séquences de pas de danses traditionnelles.
En France, les premiers travaux utilisant l’appariement optimal sont ceux de Claire Lemercier3 sur les carrières des membres des institutions consulaires parisiennes au xixe siècle (Lemercier, 2005), et de Laurent Lesnard4 sur les emplois du temps (Lesnard, 2008). Mais dès les années 1980, les chercheurs du Céreq construisaient des typologies de trajectoires d’insertion à l’aide des méthodes d’analyse des données « à la française » (analyse des correspondances, etc.)5. Au final, on dénombre maintenant plus d’une centaine d’articles de sciences sociales contenant ou discutant des techniques empruntées à l’analyse de séquences.
Pour une présentation des différentes méthodes d’analyse de séquences disponibles et de leur mise en oeuvre pratique, il existe un petit manuel en français, publié en 2011 dernière aux éditions du Ceped (collection « Les clefs pour »6) et disponible en pdf7 (Robette, 2011). De plus, un article récemment publié dans le Bulletin de Méthodologie Sociologique compare de manière systématique les résultats obtenus par les principales méthodes d’analyse de séquences (Robette & Bry, 2012). La conclusion en est qu’avec des données empiriques aussi structurées que celles que l’on utilise en sciences sociales, l’approche est robuste, c’est-à-dire qu’un changement de méthode aura peu d’influence sur les principaux résultats. Cependant, l’article tente aussi de décrire les spécificités de chaque méthode et les différences marginales qu’elles font apparaître, afin de permettre aux chercheurs de mieux adapter leurs choix méthodologiques à leur question de recherche.
Afin d’illustrer la démarche de l’analyse de séquences, nous allons procéder ici à la description « pas à pas » d’un corpus de carrières professionnelles, issues de l’enquête Biographies et entourage (Ined, 2000)8. Et pour ce faire, on va utiliser le logiciel R, qui propose la solution actuellement la plus complète et la plus puissante en matière d’analyse de séquences. Les méthodes d’analyse de séquences par analyses factorielles ou de correspondances ne nécessitent pas de logiciel spécifique : tous les logiciels de statistiques généralistes peuvent être utilisés (SAS, SPSS, Stata, R, etc.). En revanche, il n’existe pas de fonctions pour l’appariement optimal dans SAS ou SPSS. Certains logiciels gratuits implémentent l’appariement optimal (comme Chesa9 ou TDA10) mais il faut alors recourir à d’autres programmes pour dérouler l’ensemble de l’analyse (classification, représentation graphique). Stata propose le module sq11, qui dispose d’un éventail de fonctions intéressantes. Mais c’est R et le package TraMineR12, développé par des collègues de l’Université de Genève (Gabadinho et al, 2011), qui fournit la solution la plus complète et la plus puissante à ce jour : on y trouve l’appariement optimal mais aussi d’autres algorithmes alternatifs, ainsi que de nombreuses fonctions de description des séquences et de représentation graphique.
Charger TraMineR et récupérer les données
Tout d’abord, à quoi ressemblent nos données ? On a reconstruit à partir de l’enquête les carrières de 1000 hommes. Pour chacune, on connaît la position professionnelle chaque année, de l’âge de 14 ans jusqu’à 50 ans. Cette position est codée de la manière suivante : les codes 1 à 6 correspondent aux groupes socioprofessionnels de la nomenclature des PCS de l’INSEE 13 (agriculteurs exploitants ; artisans, commerçants et chefs d’entreprise ; cadres et professions intellectuelles supérieures ; professions intermédiaires ; employés ; ouvriers) ; on y a ajouté « études » (code 7), « inactivité » (code 8) et « service militaire » (code 9). Le fichier de données comporte une ligne par individu et une colonne par année : la variable csp1 correspond à la position à 14 ans, la variable csp2 à la position à 15 ans, etc. Par ailleurs, les enquêtés étant tous nés entre 1930 et 1950, on ajoute à notre base une variable « génération » à trois modalités, prenant les valeurs suivantes : 1=“1930-1938” ; 2=“1939-1945” ; 3=“1946-1950”. Au final, la base est constituée de 500 lignes et de 37 + 1 = 38 colonnes et se présente sous la forme d’un fichier texte au format csv (téléchargeable à http://larmarange.github.io/analyse-R/data/trajpro.csv).
Une fois R ouvert, on commence par installer les extensions nécessaires à ce programme (opération à ne réaliser que lors de leur première utilisation) et par les charger en mémoire. L’extension TraMineR propose de nombreuses fonctions pour l’analyse de séquences. L’extension cluster comprend un certain nombre de méthodes de classification automatique13.
TraMineR stable version 2.2-6 (Built: 2023-01-10)Website: http://traminer.unige.chPlease type 'citation("TraMineR")' for citation information.On importe ensuite les données, on recode la variable « génération » pour lui donner des étiquettes plus explicites. On jette également un coup d’oeil à la structure du tableau de données :
Rows: 1000 Columns: 38
── Column specification ────────────────────────────────────
Delimiter: ","
dbl (38): csp1, csp2, csp3, csp4, csp5, csp6, csp7, csp8...
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.donnees$generation <- factor(donnees$generation, labels = c("1930-38", "1939-45", "1946-50"))
str(donnees)spc_tbl_ [1,000 × 38] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
$ csp1 : num [1:1000] 1 7 6 7 7 6 7 7 7 6 ...
$ csp2 : num [1:1000] 1 7 6 7 7 6 7 7 6 6 ...
$ csp3 : num [1:1000] 1 7 6 6 7 6 7 7 6 6 ...
$ csp4 : num [1:1000] 1 7 6 6 7 6 7 7 6 6 ...
$ csp5 : num [1:1000] 1 7 6 6 7 6 7 7 6 6 ...
$ csp6 : num [1:1000] 1 7 6 6 7 6 9 7 6 6 ...
$ csp7 : num [1:1000] 6 9 6 6 7 6 9 7 9 6 ...
$ csp8 : num [1:1000] 6 9 9 6 7 6 9 7 4 6 ...
$ csp9 : num [1:1000] 6 6 9 6 7 6 9 3 4 9 ...
$ csp10 : num [1:1000] 6 6 9 6 7 6 4 3 4 9 ...
$ csp11 : num [1:1000] 6 6 6 6 3 6 4 3 4 6 ...
$ csp12 : num [1:1000] 6 6 6 6 3 6 4 3 4 6 ...
$ csp13 : num [1:1000] 6 6 6 6 3 6 4 3 4 6 ...
$ csp14 : num [1:1000] 6 4 6 6 3 6 4 3 4 6 ...
$ csp15 : num [1:1000] 6 4 6 6 3 6 4 3 4 6 ...
$ csp16 : num [1:1000] 6 4 6 6 3 6 6 3 4 6 ...
$ csp17 : num [1:1000] 6 4 6 6 3 6 6 3 4 6 ...
$ csp18 : num [1:1000] 6 4 6 6 3 6 6 3 4 6 ...
$ csp19 : num [1:1000] 6 4 6 6 3 6 6 3 4 6 ...
$ csp20 : num [1:1000] 6 4 6 6 3 6 6 3 4 6 ...
$ csp21 : num [1:1000] 6 4 6 6 6 6 6 3 4 6 ...
$ csp22 : num [1:1000] 6 4 6 6 6 6 6 3 4 4 ...
$ csp23 : num [1:1000] 6 4 6 6 6 6 6 3 4 4 ...
$ csp24 : num [1:1000] 6 6 6 6 5 6 6 3 4 4 ...
$ csp25 : num [1:1000] 6 6 6 6 5 6 6 3 4 4 ...
$ csp26 : num [1:1000] 6 6 6 6 5 6 6 3 4 4 ...
$ csp27 : num [1:1000] 6 6 6 6 5 6 6 3 4 4 ...
$ csp28 : num [1:1000] 6 6 6 6 5 6 6 3 4 4 ...
$ csp29 : num [1:1000] 6 6 6 6 5 6 6 3 4 4 ...
$ csp30 : num [1:1000] 4 6 6 6 5 6 6 3 4 4 ...
$ csp31 : num [1:1000] 4 6 6 6 5 6 6 3 4 4 ...
$ csp32 : num [1:1000] 4 6 6 6 5 6 6 3 4 4 ...
$ csp33 : num [1:1000] 4 6 6 6 5 6 6 3 4 4 ...
$ csp34 : num [1:1000] 4 6 6 6 5 6 6 3 4 4 ...
$ csp35 : num [1:1000] 4 6 6 6 5 6 6 3 4 4 ...
$ csp36 : num [1:1000] 4 6 6 6 5 6 6 3 4 4 ...
$ csp37 : num [1:1000] 4 6 6 6 5 6 6 3 4 4 ...
$ generation: Factor w/ 3 levels "1930-38","1939-45",..: 2 1 1 3 2 3 1 1 2 1 ...
- attr(*, "spec")=
.. cols(
.. csp1 = col_double(),
.. csp2 = col_double(),
.. csp3 = col_double(),
.. csp4 = col_double(),
.. csp5 = col_double(),
.. csp6 = col_double(),
.. csp7 = col_double(),
.. csp8 = col_double(),
.. csp9 = col_double(),
.. csp10 = col_double(),
.. csp11 = col_double(),
.. csp12 = col_double(),
.. csp13 = col_double(),
.. csp14 = col_double(),
.. csp15 = col_double(),
.. csp16 = col_double(),
.. csp17 = col_double(),
.. csp18 = col_double(),
.. csp19 = col_double(),
.. csp20 = col_double(),
.. csp21 = col_double(),
.. csp22 = col_double(),
.. csp23 = col_double(),
.. csp24 = col_double(),
.. csp25 = col_double(),
.. csp26 = col_double(),
.. csp27 = col_double(),
.. csp28 = col_double(),
.. csp29 = col_double(),
.. csp30 = col_double(),
.. csp31 = col_double(),
.. csp32 = col_double(),
.. csp33 = col_double(),
.. csp34 = col_double(),
.. csp35 = col_double(),
.. csp36 = col_double(),
.. csp37 = col_double(),
.. generation = col_double()
.. )
- attr(*, "problems")=<externalptr> On a bien 1000 observations et 38 variables. On définit maintenant des labels pour les différents états qui composent les séquences et on crée un objet « séquence » avec seqdef :
labels <- c("agric", "acce", "cadr", "pint", "empl", "ouvr", "etud", "inact", "smil")
seq <- seqdef(donnees[, 1:37], states = labels) [>] state coding: [alphabet] [label] [long label] 1 1 agric agric 2 2 acce acce 3 3 cadr cadr 4 4 pint pint 5 5 empl empl 6 6 ouvr ouvr 7 7 etud etud 8 8 inact inact 9 9 smil smil [>] 1000 sequences in the data set [>] min/max sequence length: 37/37Appariement optimal et classification
Ces étapes préalables achevées, on peut comparer les séquences en calculant les dissimilarités entre paires de séquences. On va ici utiliser la méthode la plus répandue, l’appariement optimal (optimal matching). Cette méthode consiste, pour chaque paire de séquences, à compter le nombre minimal de modifications (substitutions, suppressions, insertions) qu’il faut faire subir à l’une des séquences pour obtenir l’autre. On peut considérer que chaque modification est équivalente, mais il est aussi possible de prendre en compte le fait que les « distances » entre les différents états n’ont pas toutes la même « valeur » (par exemple, la distance sociale entre emploi à temps plein et chômage est plus grande qu’entre emploi à temps plein et emploi à temps partiel), en assignant aux différentes modifications des « coûts » distincts. Dans notre exemple, on va créer avec seqsubm une « matrice des coûts de substitution » dans laquelle tous les coûts
sont constants et égaux à 214 :
[>] creating 9x9 substitution-cost matrix using 2 as constant valueEnsuite, on calcule la matrice de distances entre les séquences (i.e contenant les « dissimilarités » entre les séquences) avec seqdist, avec un coût d’insertion/suppression (indel) que l’on fixe ici à 1 :
[>] 1000 sequences with 9 distinct states [>] checking 'sm' (size and triangle inequality) [>] 818 distinct sequences [>] min/max sequence lengths: 37/37 [>] computing distances using the OM metric [>] elapsed time: 0.89 secsCe cas de figure où tous les coûts de substitution sont égaux à 2 et le coût indel égal à 1 correspond à un cas particulier d’optimal matching que l’on appelle la Longuest Common Subsequence ou LCS. Elle peut se calculer directement avec seqdist de la manière suivante :
[>] 1000 sequences with 9 distinct states [>] creating a 'sm' with a substitution cost of 2 [>] creating 9x9 substitution-cost matrix using 2 as constant value [>] 818 distinct sequences [>] min/max sequence lengths: 37/37 [>] computing distances using the LCS metric [>] elapsed time: 0.89 secsEn l’absence d’hypothèses fortes sur les différents statuts auxquels correspond notre alphabet (données hiérarchisées, croisement de différentes dimensions…), nous vous recommandons d’utiliser prioritairement la métrique LCS pour calculer la distance entre les séquences.
On pourra trouver un exemple de matrice de coûts hiérarchisée dans le chapitre sur les trajectoires de soins.
Cette matrice des distances ou des dissimilarités entre séquences peut ensuite être utilisée pour une classification ascendante hiérarchique (CAH), qui permet de regrouper les séquences en un certain nombre de « classes » en fonction de leur proximité :
Avec la fonction plot, il est possible de tracer l’arbre de la classification (dendrogramme).

De même, on peut représenter les sauts d’inertie.
plot(sort(seq.dist$height, decreasing = TRUE)[1:20], type = "s", xlab = "nb de classes", ylab = "inertie")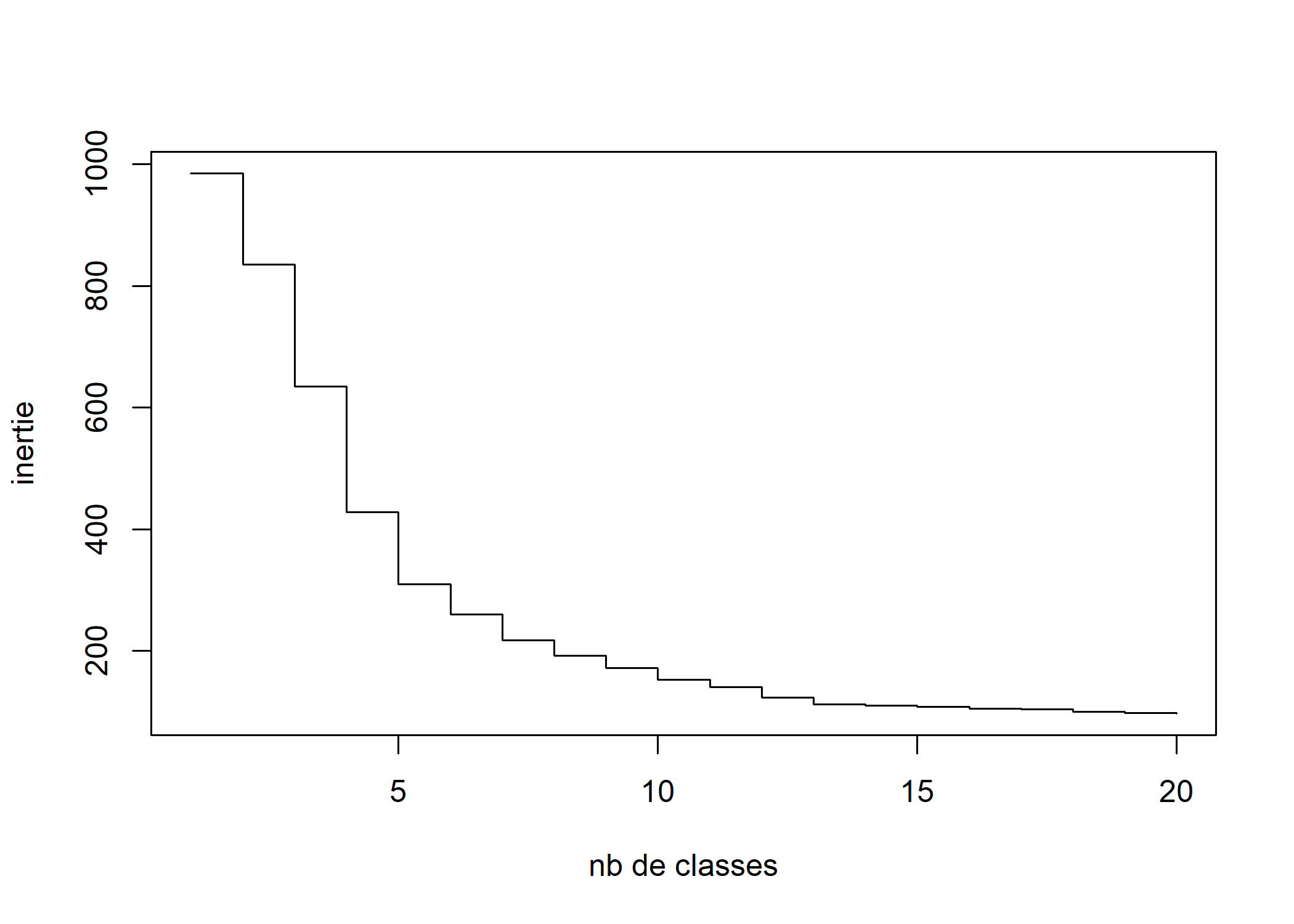
L’observation, sur ce dendogramme ou sur la courbe des sauts d’inertie, des sauts d’inertie des dernières étapes de la classification peut servir de guide pour déterminer le nombre de classes que l’on va retenir pour la suite des analyses. Une première inflexion dans la courbe des sauts d’inertie apparaît au niveau d’une partition en 5 classes. On voit aussi une seconde inflexion assez nette à 7 classes. Mais il faut garder en tête le fait que ces outils ne sont que des guides, le choix devant avant tout se faire après différents essais, en fonction de l’intérêt des résultats par rapport à la question de recherche et en arbitrant entre exhaustivité et parcimonie.
On fait ici le choix d’une partition en 5 classes :
Représentations graphiques
Pour se faire une première idée de la nature des classes de la typologie, il existe un certain nombre de représentations graphiques. Les chronogrammes (state distribution plots) présentent une série de coupes transversales : pour chaque âge, on a les proportions d’individus de la classe dans les différentes situations (agriculteur, étudiant, etc.). Ce graphique s’obtient avec seqdplot :
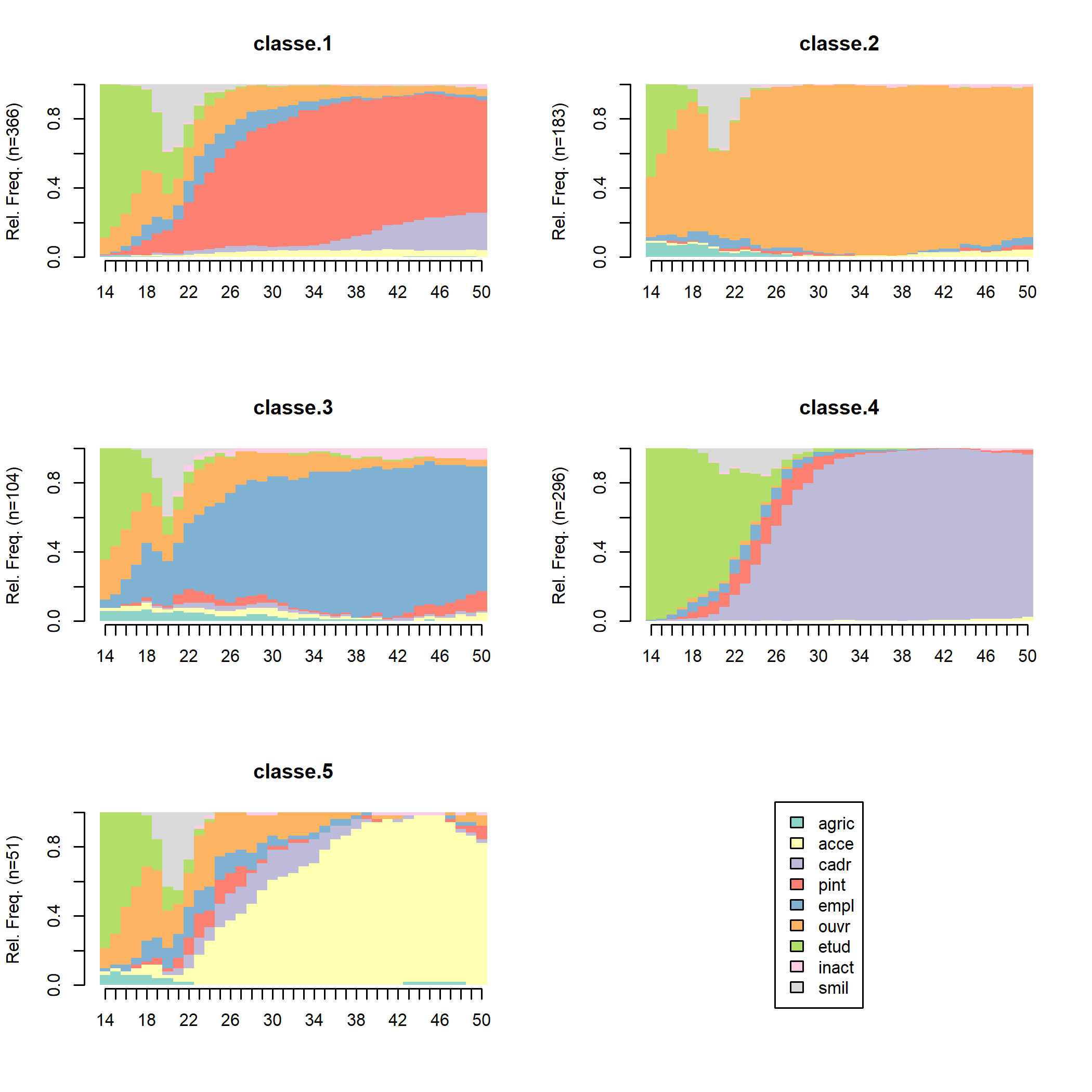
Chacune des classes semble caractérisée par un groupe professionnel principal : profession intermédiaire pour la classe 1, ouvrier pour la 2, employé pour la 3, cadre pour la 4 et indépendant pour la 5. Cependant, on aperçoit aussi des « couches » d’autres couleurs, indiquant que l’ensemble des carrières ne sont probablement pas stables.
Les « tapis » (index plots), obtenus avec seqIplot, permettent de mieux visualiser la dimension individuelle des séquences. Chaque segment horizontal représente une séquence, découpée en sous-segments correspondant aux aux différents états successifs qui composent la séquence.
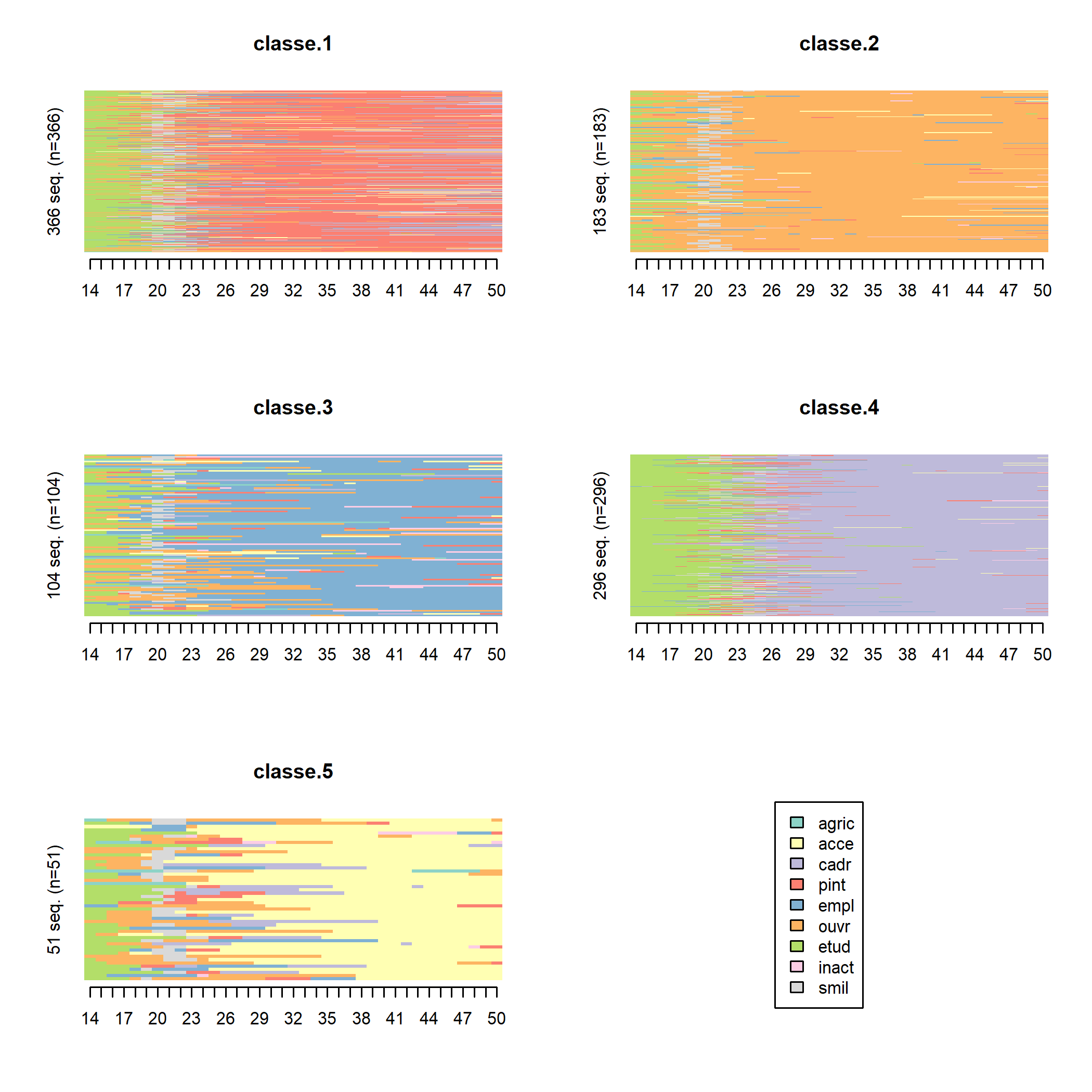
Il est possible de trier les séquences pour rendre les tapis plus lisibles (on trie ici par multidimensional scaling à l’aide de la fonction cmdscale).
ordre <- cmdscale(as.dist(seq.om), k = 1)
seqIplot(seq, group = seq.part, sortv = ordre, xtlab = 14:50, space = 0, border = NA, yaxis = FALSE)
On voit mieux apparaître ainsi l’hétérogénéité de certaines classes. Les classes 1, 3 et 4, par exemple, semblent regrouper des carrières relativement stables (respectivement de professions intermédiaires, d’employés et de cadres) et des carrières plus « mobiles » commencées comme ouvrier (classes 1 et 3, en orange) ou comme profession intermédiaire (classe 4, en rouge). De même, la majorité des membres de la dernière classe commencent leur carrière dans un groupe professionnel distinct de celui qu’ils occuperont par la suite (indépendants). Ces distinctions apparaissent d’ailleurs si on relance le programme avec un nombre plus élevé de classes (en remplaçant le 5 de la ligne nbcl <- 5 par 7, seconde inflexion de la courbe des sauts d’inertie, et en exécutant de nouveau le programme à partir de cette ligne) : les stables et les mobiles se trouvent alors dans des classes distinctes.
Le package seqhandbook propose une fonction seq_heatmap permettant de représenter le tapis de l’ensemble des séquences selon l’ordre du dendrogramme.
Attachement du package : 'seqhandbook'L'objet suivant est masqué depuis 'package:JLutils':
seq_heatmap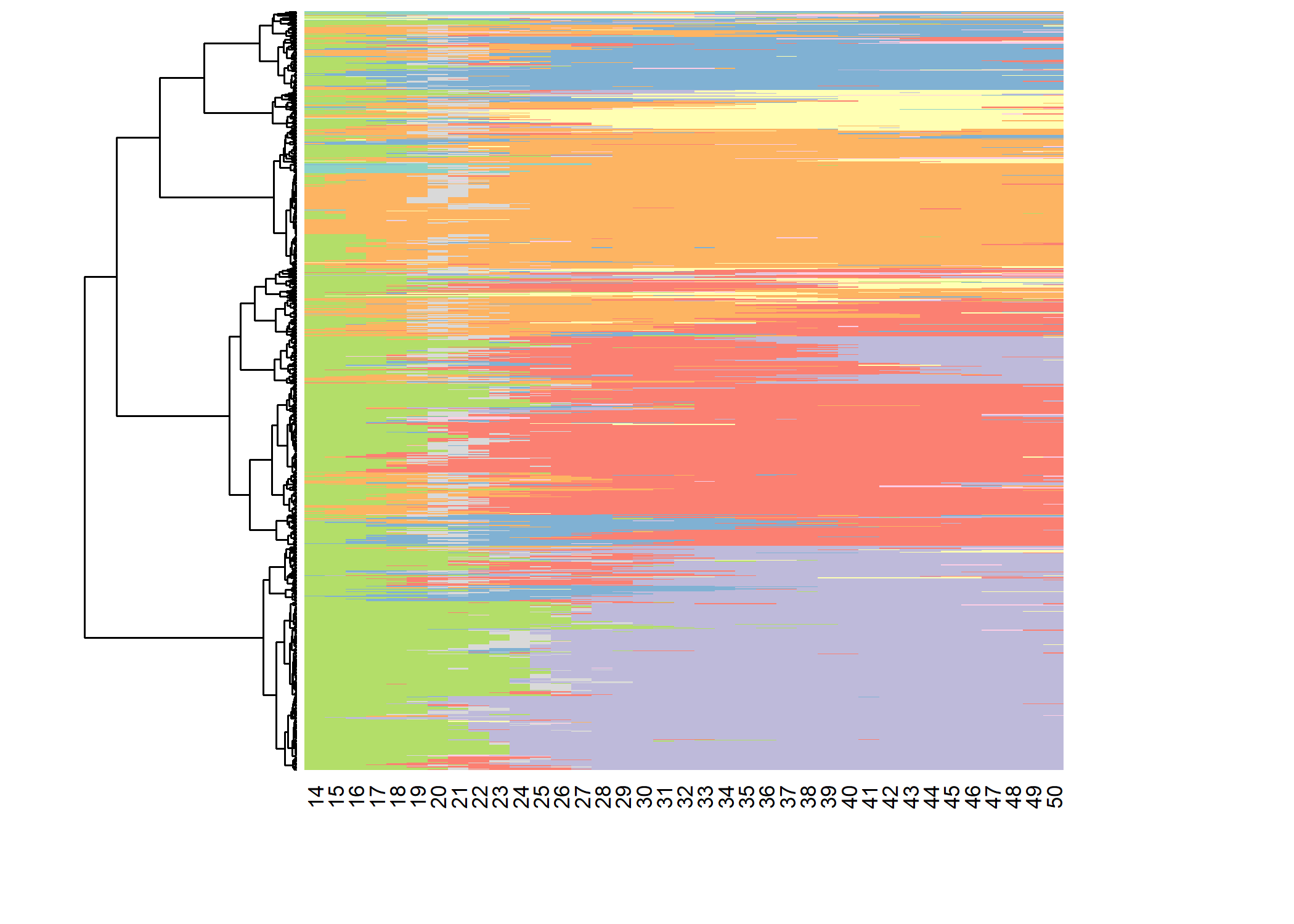
Il est possible de reproduire un tapis de séquence avec ggplot2. Outre le fait que cela fournit plus d’options de personnalisation du graphique, cela permets également à ce que la hauteur de chaque classe sur le graphique soit proportionnelle aux nombre d’invidus.
En premier lieu, on a va ajouter à notre fichier de données des identifiants individuels, la typologie crée et l’ordre obtenu par multidimensional scaling.
donnees$id <- row.names(donnees)
donnees$classe <- seq.part
donnees$ordre <- rank(ordre, ties.method = "random")Ensuite, il est impératif que nos données soient dans un format long et tidy, c’est-à-dire avec une ligne par individu et par pas de temps. Pour cela on aura recours à la fonction gather (voir le chapitre dédié).
On va mettre en forme la variable csp sous forme de facteur, récupérer l’année grace à la fonction str_sub de l’extension stringr (voir le chapitre sur la manipulation de texte) et recalculer l’âge.
long$csp <- factor(long$csp, labels = c("agriculteur", "art./com./chefs", "cadres", "prof. int.", "employés", "ouvriers", "étudiants", "inactifs", "serv. militaire"))
library(stringr)
long$annee <- as.integer(str_sub(long$annee, 4))
long$age <- long$annee + 13Il n’y a plus qu’à faire notre graphique grace à geom_raster qui permet de colorier chaque pixel. Techniquement, pour un tapis de séquence, il s’agit de représenter le temps sur l’axe horizontal et les individus sur l’axe vertical. Petite astuce : plutôt que d’utiliser id pour l’axe vertical, nous utilisons ordre afin de trier les observations. Par ailleurs, il est impératif de transformer au passage ordre en facteur afin que ggplot2 puisse recalculer proprement et séparément les axes pour chaque facette15, à condition de ne pas oublier l’option scales = "free_y" dans l’appel à facet_grid. Les autres commandes ont surtout pour vocation d’améliorer le rendu du graphique (voir le chapitre dédié à ggplot2).
library(ggplot2)
ggplot(long) +
aes(x = age, y = factor(ordre), fill = csp) +
geom_raster() +
ylab("") +
scale_y_discrete(label = NULL) +
theme_bw() +
theme(legend.position = "bottom") +
scale_fill_brewer(palette = "Set3") +
facet_grid(classe ~ ., scales = "free_y", space = "free_y") +
scale_x_continuous(limits = c(14, 50), breaks = c(14, 20, 25, 30, 35, 40, 45, 50), expand = c(0, 0))Warning: Removed 2000 rows containing missing values
(`geom_raster()`).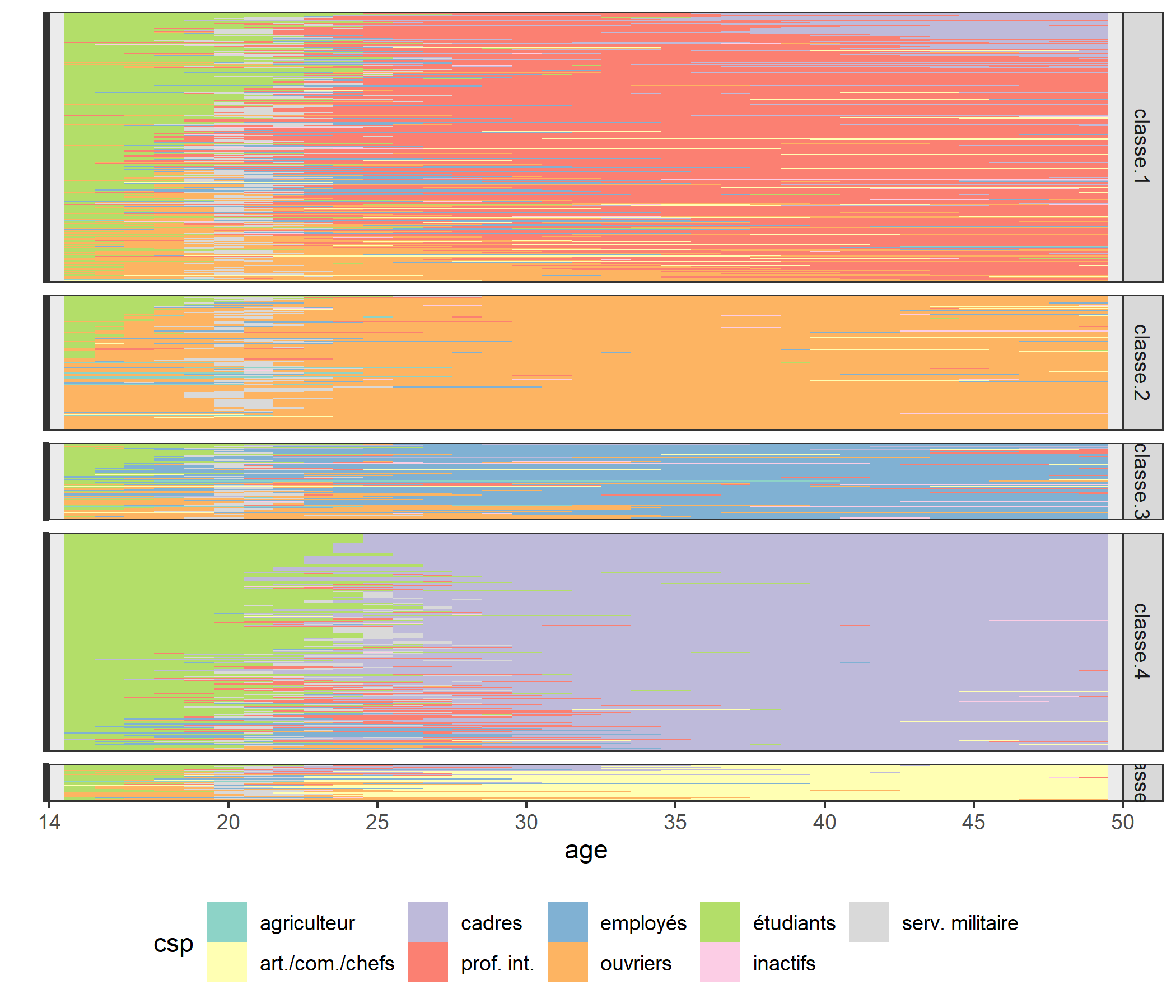
La distance des séquences d’une classe au centre de cette classe, obtenue avec disscenter, permet de mesurer plus précisément l’homogénéité des classes. Nous utilisons ici aggregate pour calculer la moyenne par classe :
Cela nous confirme que les classes 1, 3 et 5 sont nettement plus hétérogènes que les autres, alors que la classe 2 est la plus homogène.
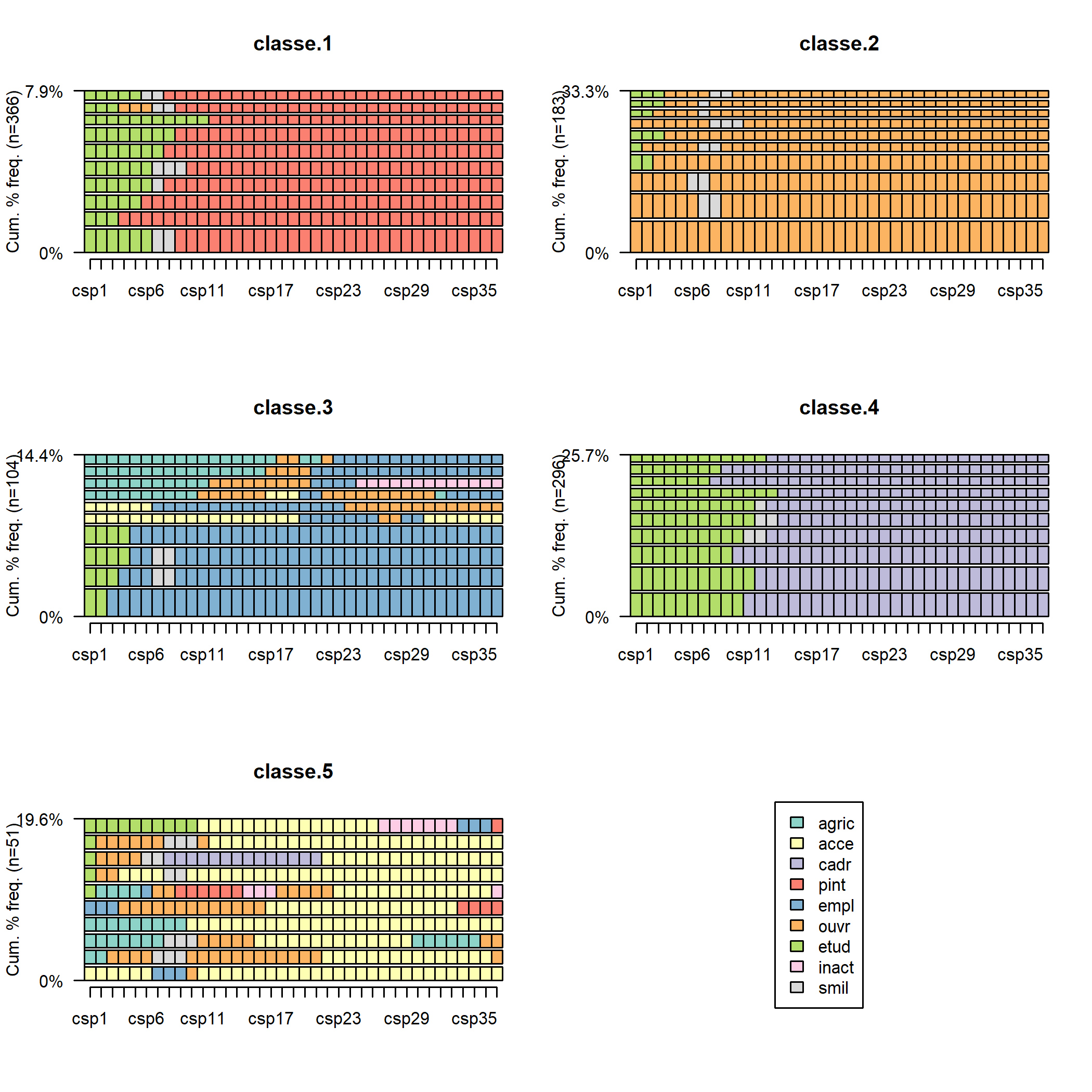
D’autres représentations graphiques existent pour poursuivre l’examen de la typologie. On peut visualiser les 10 séquences les plus fréquentes de chaque classe avec seqfplot.
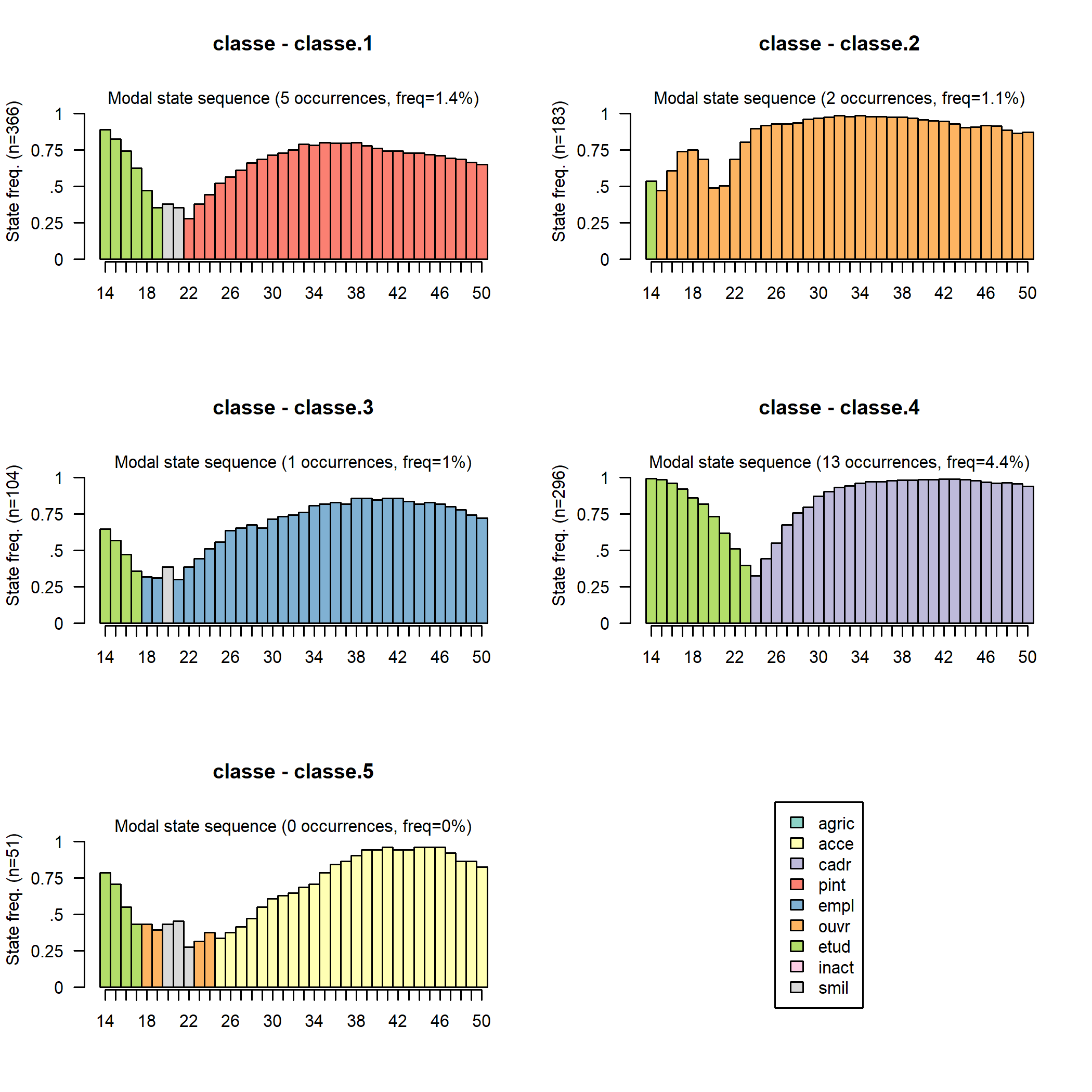
On peut aussi visualiser avec seqmsplot l’état modal (celui qui correspond au plus grand nombre de séquences de la classe) à chaque âge.
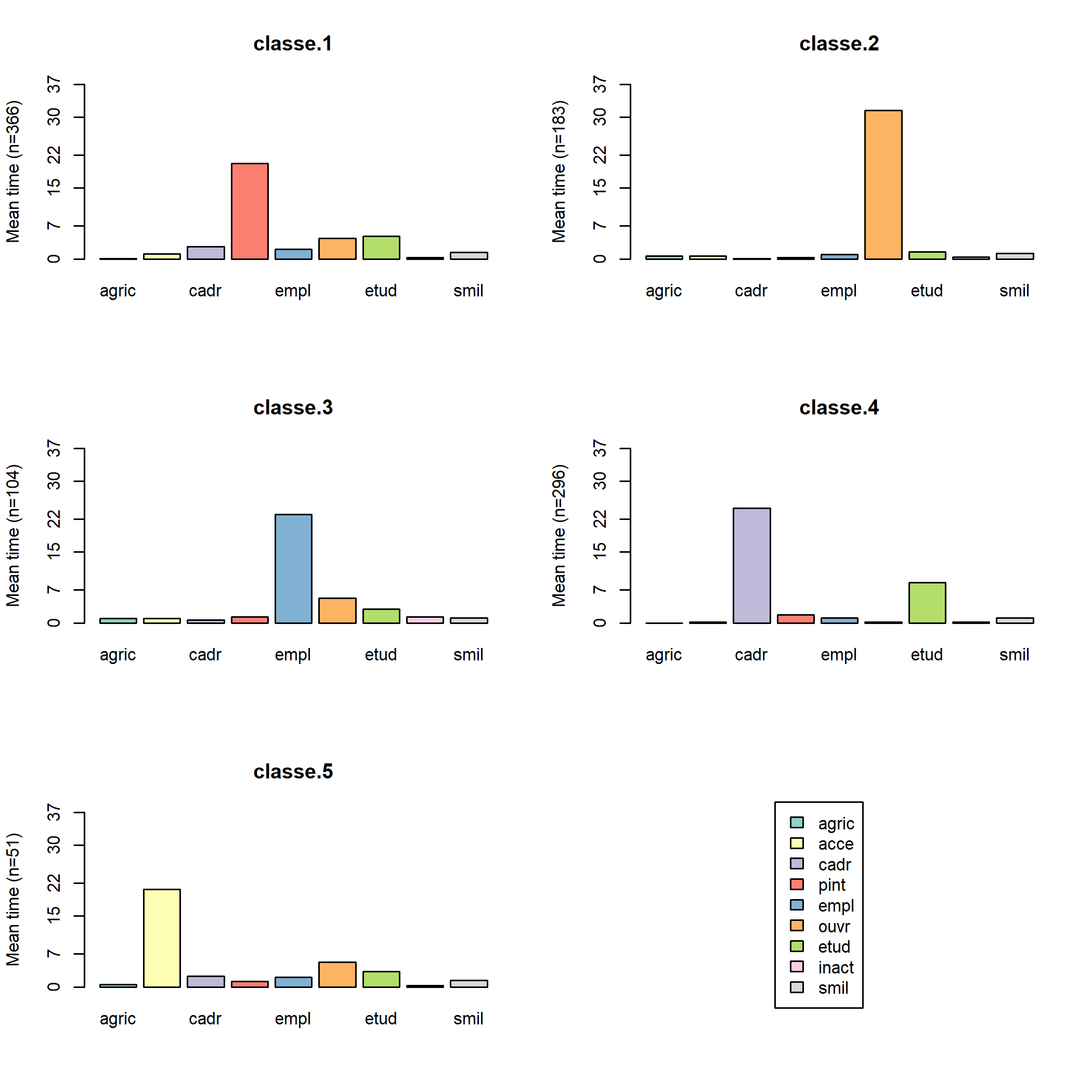
On peut également représenter avec seqmtplot les durées moyennes passées dans les différents états.
La fonction seqrplot cherche à identifier des séquences représentatives
de chaque classe. Plusieurs méthodes sont proposées (voir seqrep). La méthode dist cherche à identifier des séquences centrales à chaque classe, c’est-à-dire situées à proximité du centre de la classe. Selon l’hétérogénéité de la classe, plusieurs séquences représentatives
peuvent être renvoyées. ATTENTION : il faut être prudent dans l’interprétation de ces séquences centrales de la classe dans la mesure où elles ne rendent pas toujours compte de ce qui se passe dans la classe et où elles peuvent induire en erreur quand la classe est assez hétérogène. Il faut donc les considérer tout en ayant en tête l’ensemble du tapis de séquence pour voir si elles sont effectivement de bonnes candidates.
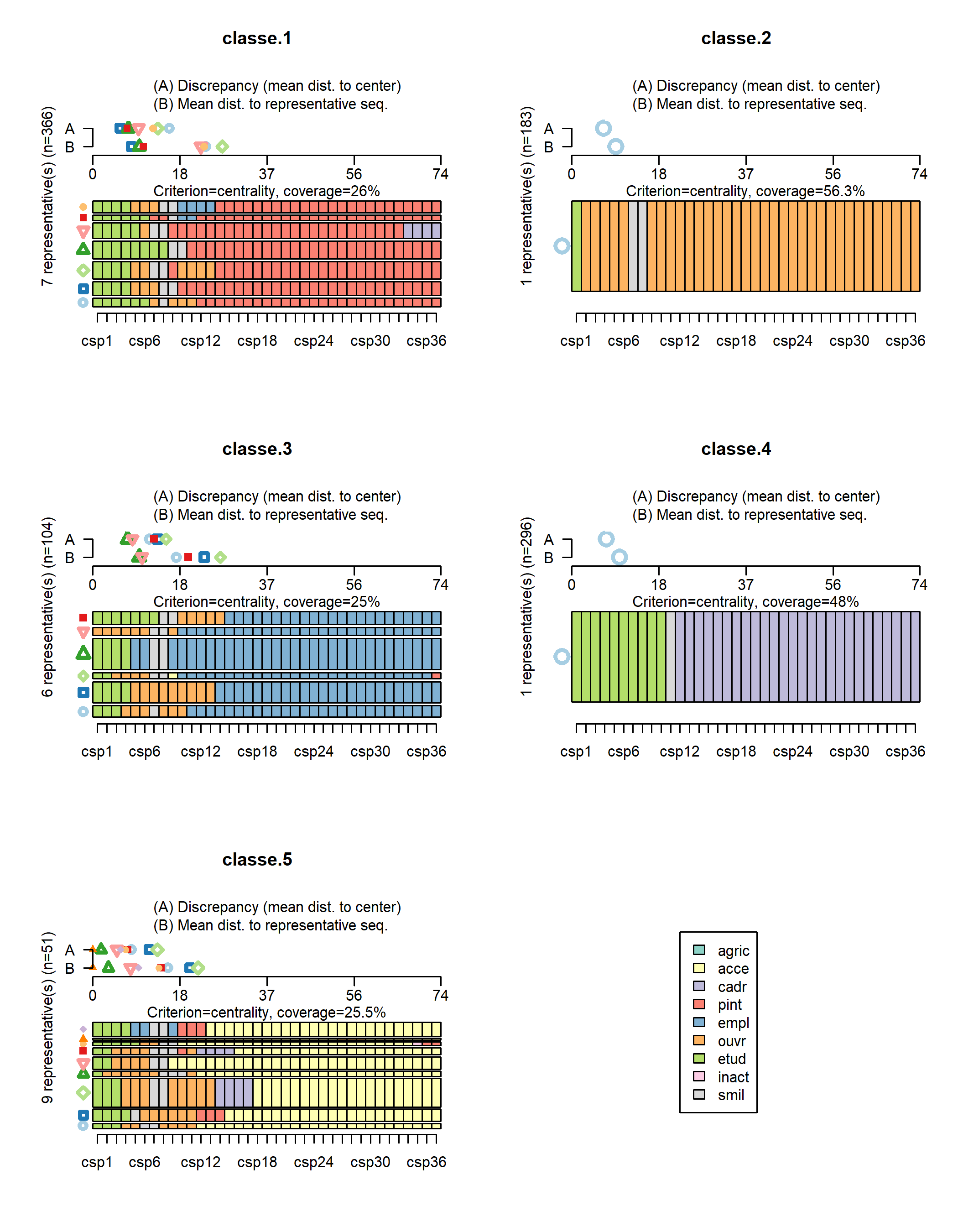
représentativesde chaque classe
Enfin, l’entropie transversale décrit l’évolution de l’homogénéité de la classe. Pour un âge donné, une entropie proche de 0 signifie que tous les individus de la classe (ou presque) sont dans la même situation. À l’inverse, l’entropie est de 1 si les individus sont dispersés dans toutes les situations. Ce type de graphique produit par seqHtplot peut être pratique pour localiser les moments de transition, l’insertion professionnelle ou une mobilité sociale ascendante.
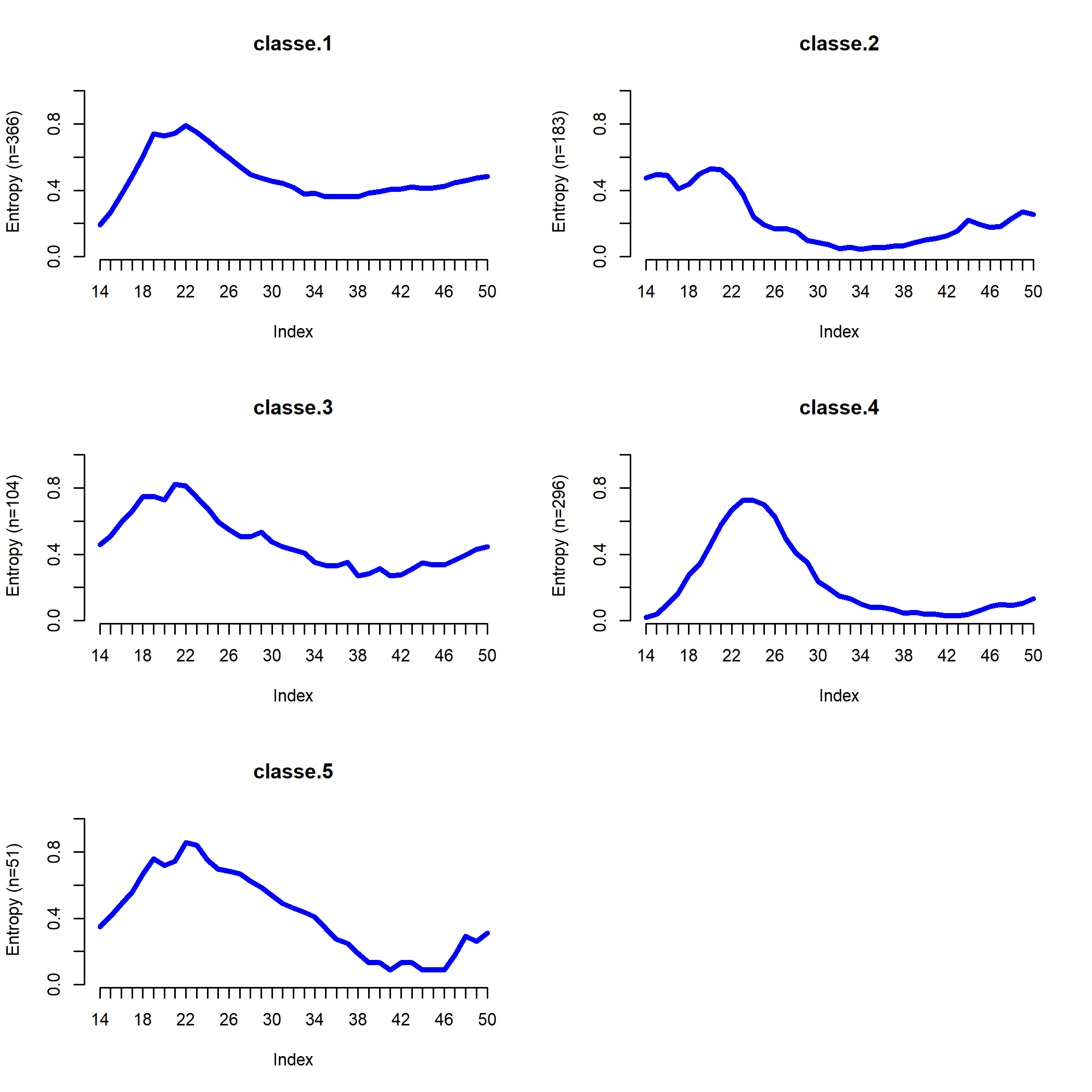
Distribution de la typologie
On souhaite maintenant connaître la distribution de la typologie (en effectifs et en pourcentages) :
On poursuit ensuite la description des classes en croisant la typologie avec la variable generation :
seq.part 1930-38 1939-45 1946-50 Ensemble
classe.1 35.6 32.5 40.8 36.6
classe.2 19.7 18.3 17.0 18.3
classe.3 6.5 13.9 11.2 10.4
classe.4 31.8 29.2 27.9 29.6
classe.5 6.5 6.1 3.0 5.1
Total 100.0 100.0 100.0 100.0
Pearson's Chi-squared test
data: table(seq.part, donnees$generation)
X-squared = 18.518, df = 8, p-value = 0.01766Le lien entre le fait d’avoir un certain type de carrières et la cohorte de naissance est significatif à un seuil de 15 %. On constate par exemple l’augmentation continue de la proportion de carrières de type « professions intermédiaires » (classe 1) et, entre les deux cohortes les plus anciennes, l’augmentation de la part des carrières de type « employés » (classe 3) et la baisse de la part des carrières de type « cadres » (classe 4).
Bien d’autres analyses sont envisageables : croiser la typologie avec d’autres variables (origine sociale, etc.), construire l’espace des carrières possibles, étudier les interactions entre trajectoires familiales et professionnelles, analyser la variance des dissimilarités entre séquences en fonction de plusieurs variables « explicatives16 »…
Mais l’exemple proposé est sans doute bien suffisant pour une première introduction !
Pour aller plus loin
En premier lieu, la lecture du manuel d’utilisation de TraMineR, intitulé Mining sequence data in R with the TraMineR package: A user’s guide et écrit par Alexis Gabadinho, Gilbert Ritschard, Matthias Studer et Nicolas S. Muller, est fortement conseillée. Ce manuel ne se contente pas de présenter l’extension, mais aborde également la théorie sous-jacente de l’analyse de séquences, les différents formats de données, les différences approches (séquences de statut ou séquences de transitions par exemple), etc.
Pour une initiation en français, on pourra se référer à l’ouvrage de Nicolas Robette Explorer et décrire les parcours de vie : les typologies de trajectoires sorti en 2011 aux éditions du Ceped.
L’extension WeightedCluster de Matthias Studer est un excellent complément à TraMineR. Il a également écrit un manuel de la librairie WeightedCluster : un guide pratique pour la création de typologies de trajectoires en sciences sociales avec R.
Enfin, l’extension TraMineRextras (https://cran.r-project.org/package=TraMineRextras) contient des fonctions complémentaires à TraMineR, plus ou moins en phase de test.
Bibliographie
- Abbott A., 2001, Time matters. On theory and method, The University of Chicago Press.
- Abbott A., Hrycak A., 1990, « Measuring ressemblance in sequence data: an optimal matching analysis of musicians’ careers», American journal of sociology, (96), p.144-185. http://www.jstor.org/stable/10.2307/2780695
- Abbott A., Tsay A., 2000, « Sequence analysis and optimal matching methods in sociology: Review and prospect », Sociological methods & research, 29(1), p.3-33. http://smr.sagepub.com/content/29/1/3.short
- Gabadinho, A., Ritschard, G., Müller, N.S. & Studer, M., 2011, « Analyzing and visualizing state sequences in R with TraMineR », Journal of Statistical Software, 40(4), p.1-37. http://archive-ouverte.unige.ch/downloader/vital/pdf/tmp/4hff8pe6uhukqiavvgaluqmjq2/out.pdf
- Grelet Y., 2002, « Des typologies de parcours. Méthodes et usages », Document Génération 92, (20), 47 p. http://www.cmh.greco.ens.fr/programs/Grelet_typolparc.pdf
- Lelièvre É., Vivier G., 2001, « Évaluation d’une collecte à la croisée du quantitatif et du qualitatif : l’enquête Biographies et entourage », Population, (6), p.1043-1073. http://www.persee.fr/web/revues/home/prescript/article/pop_0032-4663_2001_num_56_6_7217
- Lemercier C., 2005, « Les carrières des membres des institutions consulaires parisiennes au XIXe siècle », Histoire et mesure, XX (1-2), p.59-95. http://histoiremesure.revues.org/786
- Lesnard L., 2008, « Off-Scheduling within Dual-Earner Couples: An Unequal and Negative Externality for Family Time », American Journal of Sociology, 114(2), p.447-490. http://laurent.lesnard.free.fr/IMG/pdf/lesnard_2008_off-scheduling_within_dual-earner_couples-2.pdf
- Lesnard L., Saint Pol T. (de), 2006, « Introduction aux Méthodes d’Appariement Optimal (Optimal Matching Analysis) », Bulletin de Méthodologie Sociologique, 90, p.5-25. http://bms.revues.org/index638.html
- Robette N., 2011, Explorer et décrire les parcours de vie : les typologies de trajectoires, Ceped (Les Clefs pour), 86 p. http://nicolas.robette.free.fr/Docs/Robette2011_Manuel_TypoTraj.pdf
- Robette N., 2012, « Du prosélytisme à la sécularisation. Le processus de diffusion de l’Optimal Matching Analysis », document de travail. http://nicolas.robette.free.fr/Docs/Proselytisme_secularisation_NRobette.pdf
- Robette N., Bry X., 2012, « Harpoon or bait? A comparison of various metrics to fish for life course patterns », Bulletin de Méthodologie Sociologique, 116, p.5-24. http://nicolas.robette.free.fr/Docs/Harpoon_maggot_RobetteBry.pdf
- Robette N., Thibault N., 2008, « L’analyse exploratoire de trajectoires professionnelles : analyse harmonique qualitative ou appariement optimal ? », Population, 64(3), p.621-646. http://www.cairn.info/revue-population-2008-4-p-621.htm
- Savage M., 2009, « Contemporary Sociology and the Challenge of Descriptive Assemblage », European Journal of Social Theory, 12(1), p.155-174. http://est.sagepub.com/content/12/1/155.short
Pour une analyse des conditions sociales de la diffusion de l’analyse de séquences dans le champ des sciences sociales, voir Robette, 2012.↩︎
Voir par exemple l’article d’Yvette Grelet (2002).↩︎
http://nicolas.robette.free.fr/Docs/Robette2011_Manuel_TypoTraj.pdf↩︎
Pour une analyse plus poussée de ces données, avec deux méthodes différentes, voir Robette & Thibault, 2008. Pour une présentation de l’enquête, voir Lelièvre & Vivier, 2001.↩︎
Pour une présentation plus détaillée, voir le chapitre sur la classification ascendante hiérarchique (CAH).↩︎
Le fonctionnement de l’algorithme d’appariement optimal — et notamment le choix des coûts — est décrit dans le chapitre 9 du manuel de
TraMineR(http://mephisto.unige.ch/pub/TraMineR/doc/TraMineR-Users-Guide.pdf).↩︎Essayez le même code mais avec
y = ordreau lieu dey = factor(ordre)et vous comprendrez tout l’intérêt de cette astuce.↩︎L’articulation entre méthodes « descriptives » et méthodes « explicatives » est un prolongement possible de l’analyse de séquences. Cependant, l’analyse de séquences était envisagée par Abbott comme une alternative à la sociologie quantitative mainstream, i.e le « paradigme des variables » et ses hypothèses implicites souvent difficilement tenables (Abbott, 2001). Une bonne description solidement fondée théoriquement vaut bien des « modèles explicatifs » (Savage, 2009).↩︎

