Dans les modèles de régression (modèles linéaires ou modèles linéaires généralisés comme la régression logistique), une transformation des variables catégorielles est nécessaire pour qu’elles puissent être prises en compte dans le modèle. On va dès lors définir des contrastes.

De manière générale, une variable catégorielle à n modalités va être transformée en n-1 variables quantitatives. Il existe cependant plusieurs manières de faire (i.e. plusieurs types de contrastes). Et, selon les contrastes choisis, les coefficients du modèles ne s’interpréteront pas de la même manière.

Contrastes de type traitement

Par défaut, R applique des contrastes de type traitement pour un facteur non ordonné. Il s’agit notamment des contrastes utilisés dans le chapitre sur la régression logistique.

Exemple 1 : un modèle linéaire avec une variable catégorielle

Commençons avec un premier exemple que nous allons calculer avec le jeu de données trial chargé en mémoire lorsque l’on appelle l’extension gtsummary. Ce jeu de données contient les observations de 200 patients. Nous nous intéressons à deux variables en particulier : marker une variable numérique correspondant à un marqueur biologique et grade un facteur à trois modalités correspondant à différent groupes de patients.

Regardons la moyenne de marker pour chaque valeur de grade.

library(gtsummary)
trial %>%
  select(marker, grade) %>%
  tbl_summary(
    by = grade,
    statistic = marker ~ "{mean}",
    digits = marker ~ 4
  ) %>%
  add_overall(last = TRUE)
Caractéristique I, N = 681 II, N = 681 III, N = 641 Total, N = 2001
Marker Level (ng/mL) 1,0669 0,6805 0,9958 0,9160
    Manquant 2 5 3 10
1 Moyenne

Utilisons maintenant une régression linaire pour modéliser la valeur de marker en fonction de grade.

mod <- lm(marker ~ grade, data = trial)
mod

Call:
lm(formula = marker ~ grade, data = trial)

Coefficients:
(Intercept)      gradeII     gradeIII  
     1.0669      -0.3864      -0.0711

Le modèle obtenu contient trois coefficients ou termes : un intercept et deux termes associés à la variable grade.

Pour bien interpréter ces coefficients, il faut comprendre comment la variable grade a été transformée avant d’être inclue dans le modèle. Nous pouvons voir cela avec la fonction contrasts.

contrasts(trial$grade)
    II III
I    0   0
II   1   0
III  0   1

Ce que nous montre cette matrice, c’est que la variable catégorielle grade à 3 modalités a été transformée en 2 variables binaires que l’on retrouve sous les noms de gradeII et gradeIII dans le modèle : gradeII vaut 1 si grade est égal à II et 0 sinon; gradeIII vaut 1 si grade est égal à III et 0 sinon. Si grade est égal à I, alors gradeII et gradeIII valent 0.

Il s’agit ici d’un contraste dit de traitement ou la première modalité joue ici le rôle de modalité de référence.

Dans ce modèle linéaire, la valeur de l’intercept correspond à la moyenne de marker lorsque nous nous trouvons à la référence, donc quand grade est égal à I dans cet exemple. Et nous pouvons le constater dans notre tableau précédent des moyennes, 1.0669 correspond bien à la moyenne de marker pour la modalité I.

La valeur du coefficient associé à markerII correspond à l’écart par rapport à la référence lorsque marker est égal à II. Autrement dit, la moyenne de marker pour la modalité II correspond à la somme de l’intercept et du coefficient markerII. Et nous retrouvons bien la relation suivante : 0.6805 = 1.0669 + -0.3864. De même, la moyenne de marker lorsque grade vaut III est égale à la somme de l’intercept et du terme markerIII.

Lorsqu’on utilise des contrastes de type traitement, chaque terme du modèle peut être associé à une et une seule modalité d’origine de la variable catégorielle. Dès lors, il est possible de rajouter la modalité de référence lorsque l’on présente les résultats et on peut même lui associer la valeurs 0, ce qui peut être fait avec tbl_regression de l’extension gtsummary avec l’option add_estimate_to_reference_rows = TRUE.

mod %>%
  tbl_regression(
    intercept = TRUE,
    add_estimate_to_reference_rows = TRUE
  )
Caractéristique Beta 95% IC1 p-valeur
(Intercept) 1,1 0,86 – 1,3 <0,001
Grade
    I 0,00 —
    II -0,39 -0,68 – -0,09 0,010
    III -0,07 -0,37 – 0,23 0,6
1 IC = intervalle de confiance

Exemple 2 : une régression logistique avec deux variables catégorielles

Pour ce deuxème exemple, nous allons utiliser le jeu de données hdv2003 fourni par l’extension questionr et recoder la variable age en groupes d’âges à 4 modalités.

library(questionr)
data("hdv2003")

library(tidyverse)
hdv2003 <- hdv2003 %>%
  mutate(
    groupe_age = cut(
      age,
      c(16, 25, 45, 65, 99),
      right = FALSE,
      include.lowest = TRUE
    ) %>%
      fct_recode(
        "16-24" = "[16,25)",
        "25-44" = "[25,45)",
        "45-64" = "[45,65)",
        "65+" = "[65,99]"
      )
  ) %>%
  labelled::set_variable_labels(
    groupe_age = "Groupe d'âges",
    sexe = "Sexe"
  )

Nous allons faire une régression logistique binaire pour investiguer l’effet du sexe (variable à 2 modalités) et du groupe d’âges (variable à 4 modalités) sur la pratique du sport.

mod <- glm(sport ~ sexe + groupe_age, family = binomial, data = hdv2003)
mod

Call:  glm(formula = sport ~ sexe + groupe_age, family = binomial, data = hdv2003)

Coefficients:
    (Intercept)        sexeFemme  groupe_age25-44  
         0.9021          -0.4455          -0.6845  
groupe_age45-64    groupe_age65+  
        -1.6535          -2.3198  

Degrees of Freedom: 1999 Total (i.e. Null);  1995 Residual
Null Deviance:      2617 
Residual Deviance: 2385     AIC: 2395

Le modèle contient 5 termes : 1 intercept, 1 coefficient pour la variable sexe et 3 coefficients pour la variable groupe_age. Comme précédent, nous pouvons constater que les variables à n modalités sont remplacées par défaut (contrastes de type traitement) par n-1 variables binaires, la première modalité jouant à chaque fois le rôle de modalité de référence.

contrasts(hdv2003$sexe)
      Femme
Homme     0
Femme     1
contrasts(hdv2003$groupe_age)
      25-44 45-64 65+
16-24     0     0   0
25-44     1     0   0
45-64     0     1   0
65+       0     0   1

L’intercept correspond donc à la situation à la référence, c’est-à-dire à la prédiction du modèle pour les hommes (référence de sexe) âgés de 16 à 24 ans (référence de groupe_age).

Il est possible d’exprimer cela en termes de probabilité en utilisant l’inverse de la fonction logit (puisque nous avons utilisé un modèle logit).

inv_logit <- binomial("logit")$linkinv
inv_logit(0.9021)
[1] 0.7113809

Selon le modèle, les hommes âgés de 16 à 24 ans ont donc 71% de chance de pratiquer du sport.

Regardons maintenant le coefficient associé à sexeFemme (-0.4455) : il représente (pour la modalité de référence des autres variables, soit pour les 16-24 ans ici) la correction à appliquer à l’intercept pour obtenir la probabilité de faire du sport. Il s’agit donc de la différence entre les femmes et les hommes pour le groupe des 16-24 ans.

inv_logit(0.9021 - 0.4455)
[1] 0.6122073

Autrement dit, selon le modèle, la probabilité de faire du sport pour une femme âgée de 16 à 24 ans est de 61%. On peut représenter cela avec la fonction ggpredict de ggeffects, qui représente les prédictions d’une variable, toutes les autres variables étant à la référence.

library(ggeffects, quietly = TRUE)

Attachement du package : 'ggeffects'
L'objet suivant est masqué depuis 'package:cowplot':

    get_title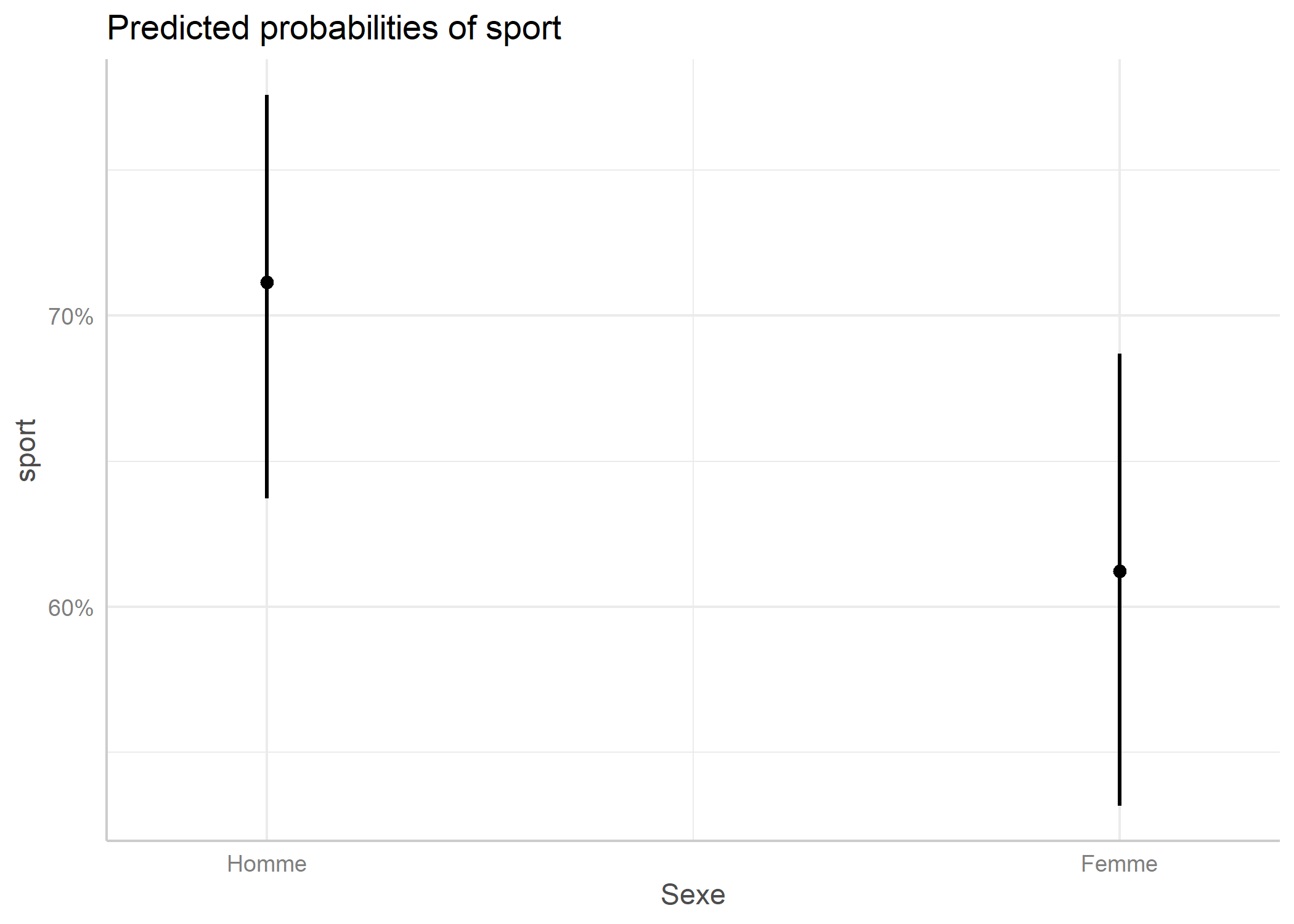
ggpredict(mod, "sexe") %>% plot()

Bien souvent, pour une régression logistique, on préfère représenter les exponentielles des coefficients qui correspondent à des odds ratios.

mod %>%
  tbl_regression(
    exponentiate = TRUE,
    intercept = TRUE,
    add_estimate_to_reference_rows = TRUE
  )
Caractéristique OR1 95% IC1 p-valeur
(Intercept) 2,46 1,76 – 3,48 <0,001
Sexe
    Homme 1,00 —
    Femme 0,64 0,53 – 0,78 <0,001
Groupe d'âges
    16-24 1,00 —
    25-44 0,50 0,35 – 0,71 <0,001
    45-64 0,19 0,13 – 0,27 <0,001
    65+ 0,10 0,06 – 0,15 <0,001
1 OR = rapport de cotes, IC = intervalle de confiance

Or, 0,64 correspond bien à l’odds ratio entre 61% et 71% (que l’on peut calculer avec odds.ratio de questionr).

odds.ratio(0.6122, 0.7114)
[1] 0.6404246

De la même manière, les différents coefficients associés à groupe_age correspondent à la différence entre chaque groupe d’âges et sa modalité de référence (ici 16-24 ans), quand les autres variables (ici le sexe) sont à leur référence (ici les hommes).

Pour prédire la probabilité de faire du sport pour un profil particulier, il faut prendre en compte toutes les termes qui s’appliquent et qui s’ajoutent à l’intercept. Par exemple, pour une femme de 50 ans il faut considérer l’intercept (0.9021), le coefficient sexeFemme (-0.4455) et le coefficient groupe_age45-64 (-1.6535). Sa probabilité de faire du sport est donc de 23%.

inv_logit(0.9021 - 0.4455 - 1.6535)
[1] 0.2320271

Changer la modalité de référence

Il est possible de personnaliser les contrastes à utiliser et avoir un recours à un contraste de type traitement mais en utilisant une autre modalité que la première comme référence, avec la fonction contr.treatment. Le premier argument de la fonction corresponds au nombre de modalités de la variable et le paramètre base permets de spécifier la modalité de référence (1 par défaut).

contr.treatment(4, base = 2)
  1 3 4
1 1 0 0
2 0 0 0
3 0 1 0
4 0 0 1

contr.SAS permets de spécifier un contraste de type traitement dont la modalité de référence est la dernière.

contr.SAS(4)
  1 2 3
1 1 0 0
2 0 1 0
3 0 0 1
4 0 0 0

Les contrastes peuvent être modifiés de deux manières : au moment de la construction du modèle (via l’option contrasts) ou comme attribut des variables (via la fonction contrasts).

contrasts(hdv2003$sexe) <- contr.SAS(2)
mod2 <- glm(
  sport ~ sexe + groupe_age,
  family = binomial,
  data = hdv2003,
  contrasts = list(groupe_age = contr.treatment(4, 3))
)
mod2 %>% tbl_regression(exponentiate = TRUE, intercept = TRUE)
Caractéristique OR1 95% IC1 p-valeur
(Intercept) 0,30 0,25 – 0,36 <0,001
Sexe
    Homme 1,56 1,29 – 1,90 <0,001
    Femme — —
Groupe d'âges
    16-24 5,23 3,67 – 7,52 <0,001
    25-44 2,64 2,12 – 3,29 <0,001
    45-64 — —
    65+ 0,51 0,37 – 0,70 <0,001
1 OR = rapport de cotes, IC = intervalle de confiance

Comme les modalités de référence ont changé, l’intercept et les différents terms ont également changé (puisque l’on ne compare plus à la même référence).

library(GGally)
ggcoef_compare(list(mod, mod2), exponentiate = TRUE, type = "f")

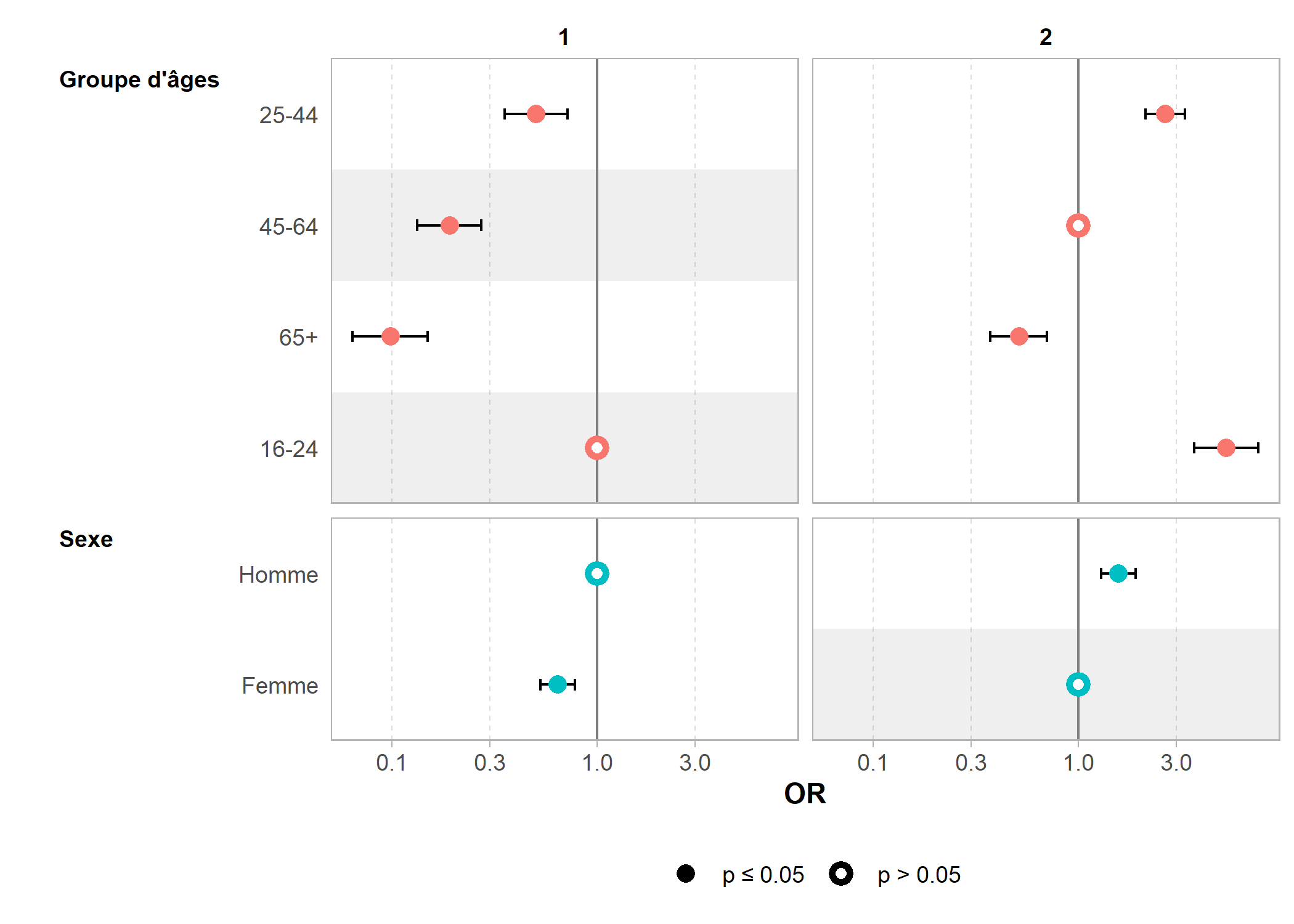
Cependant, du point de vue explicatif et prédictif, les deux modèles sont rigoureusement identiques.

anova(mod, mod2)

Contrastes de type somme

mod <- lm(marker ~ grade, data = trial, contrasts = list(grade = contr.sum))
mod

Call:
lm(formula = marker ~ grade, data = trial, contrasts = list(grade = contr.sum))

Coefficients:
(Intercept)       grade1       grade2  
     0.9144       0.1525      -0.2339  
mod %>%
  tbl_regression(
    add_estimate_to_reference_rows = TRUE,
    intercept = TRUE
  )
Caractéristique Beta 95% IC1 p-valeur
(Intercept) 0,91 0,79 – 1,0 <0,001
Grade
    I 0,15 -0,02 – 0,32 0,078
    II -0,23 -0,41 – -0,06 0,008
    III 0,08 —
1 IC = intervalle de confiance