Une version actualisée de ce chapitre est disponible sur guide-R : Interactions

Ce chapitre est évoqué dans le webin-R #07 (régression logistique partie 2) sur YouTube.

Dans un modèle statistique classique, on fait l’hypothèse implicite que chaque variable explicative est indépendante des autres. Cependant, cela ne se vérifie pas toujours. Par exemple, l’effet de l’âge peut varier en fonction du sexe. Il est dès lors nécessaire de prendre en compte dans son modèle les effets d’interaction1.

Exemple d’interaction

Reprenons le modèle que nous avons utilisé dans le chapitre sur la régression logistique.

library(questionr)
data(hdv2003)
d <- hdv2003
d$sexe <- relevel(d$sexe, "Femme")
d$grpage <- cut(d$age, c(16, 25, 45, 65, 99), right = FALSE, include.lowest = TRUE)
d$etud <- d$nivetud
levels(d$etud) <- c(
  "Primaire", "Primaire", "Primaire",
  "Secondaire", "Secondaire", "Technique/Professionnel",
  "Technique/Professionnel", "Supérieur"
)
d$etud <- addNAstr(d$etud, "Manquant")
library(labelled)
var_label(d$sport) <- "Pratique du sport ?"
var_label(d$sexe) <- "Sexe"
var_label(d$grpage) <- "Groupe d'âges"
var_label(d$etud) <- "Niveau d'étude"
var_label(d$relig) <- "Pratique religieuse"
var_label(d$heures.tv) <- "Nombre d'heures passées devant la télévision par jour"

Nous avions alors exploré les facteurs associés au fait de pratiquer du sport.

mod <- glm(sport ~ sexe + grpage + etud + heures.tv + relig, data = d, family = binomial())
library(gtsummary)
tbl_regression(mod, exponentiate = TRUE)
Caractéristique OR1 95% IC1 p-valeur
Sexe
    Femme — —
    Homme 1,55 1,26 – 1,91 <0,001
Groupe d'âges
    [16,25) — —
    [25,45) 0,66 0,42 – 1,03 0,065
    [45,65) 0,34 0,21 – 0,54 <0,001
    [65,99] 0,25 0,15 – 0,43 <0,001
Niveau d'étude
    Primaire — —
    Secondaire 2,59 1,77 – 3,83 <0,001
    Technique/Professionnel 2,86 1,98 – 4,17 <0,001
    Supérieur 6,63 4,55 – 9,80 <0,001
    Manquant 8,59 4,53 – 16,6 <0,001
Nombre d'heures passées devant la télévision par jour 0,89 0,83 – 0,95 <0,001
Pratique religieuse
    Pratiquant regulier — —
    Pratiquant occasionnel 0,98 0,68 – 1,42 >0,9
    Appartenance sans pratique 0,99 0,71 – 1,40 >0,9
    Ni croyance ni appartenance 0,81 0,55 – 1,18 0,3
    Rejet 0,68 0,39 – 1,19 0,2
    NSP ou NVPR 0,92 0,40 – 2,02 0,8
1 OR = rapport de cotes, IC = intervalle de confiance

Selon les résultats de notre modèle, les hommes pratiquent plus un sport que les femmes et la pratique du sport diminue avec l’âge. Pour représenter les effets différentes variables, on peut avoir recours à la fonction allEffects de l’extension effects.

library(effects)
Le chargement a nécessité le package : carData
lattice theme set by effectsTheme()
See ?effectsTheme for details.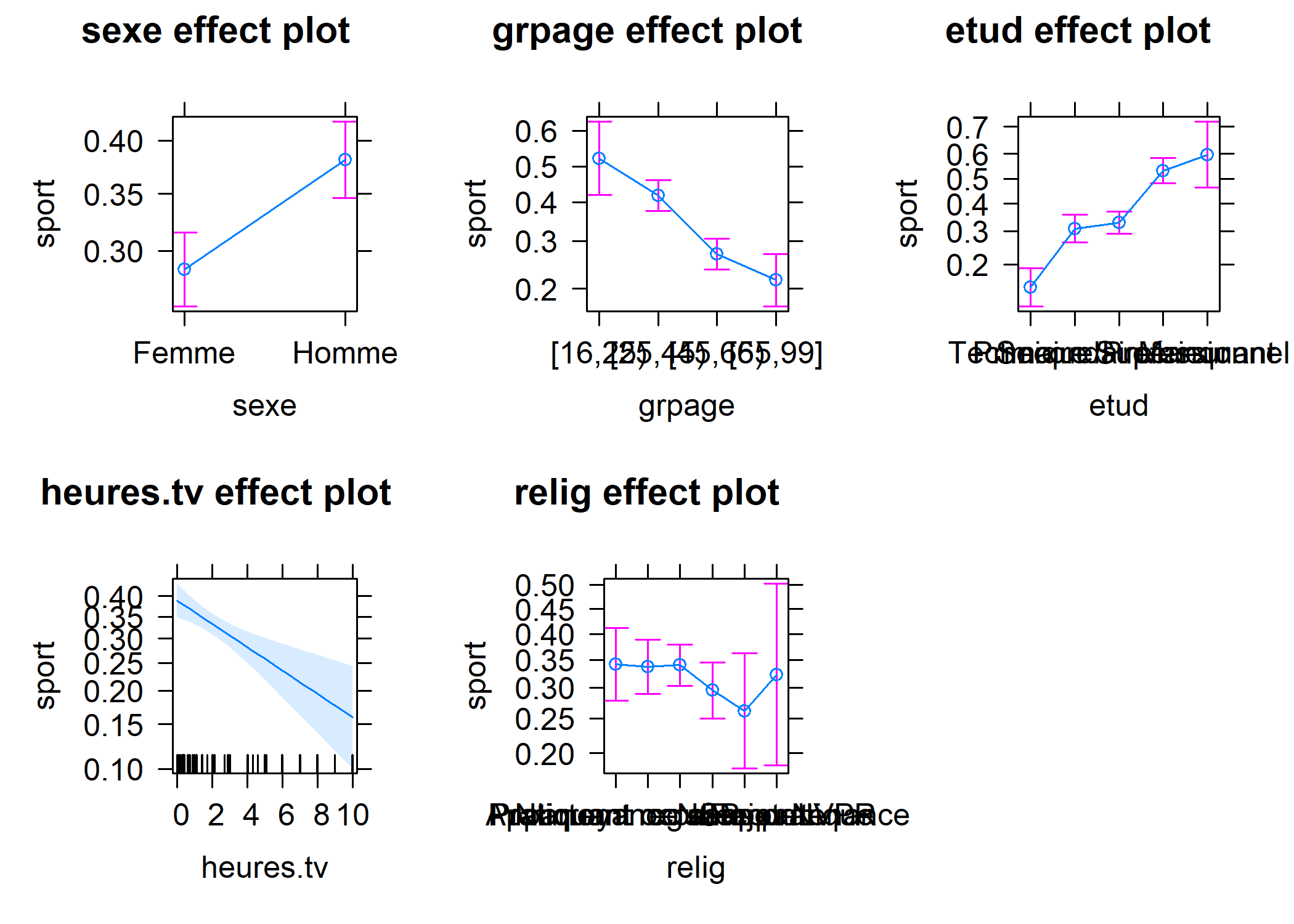
plot(allEffects(mod))
Représentation graphique des effets du modèle

Cependant, l’effet de l’âge est-il le même selon le sexe ? Nous allons donc introduire une interaction entre l’âge et le sexe dans notre modèle, ce qui sera représenté par sexe * grpage dans l’équation du modèle.

mod2 <- glm(sport ~ sexe * grpage + etud + heures.tv + relig, data = d, family = binomial())
tbl_regression(mod2, exponentiate = TRUE)
Caractéristique OR1 95% IC1 p-valeur
Sexe
    Femme — —
    Homme 5,20 2,46 – 11,7 <0,001
Groupe d'âges
    [16,25) — —
    [25,45) 1,02 0,59 – 1,80 >0,9
    [45,65) 0,61 0,34 – 1,10 0,10
    [65,99] 0,46 0,23 – 0,92 0,027
Niveau d'étude
    Primaire — —
    Secondaire 2,60 1,77 – 3,85 <0,001
    Technique/Professionnel 2,88 1,99 – 4,21 <0,001
    Supérieur 6,77 4,64 – 10,0 <0,001
    Manquant 9,02 4,68 – 17,8 <0,001
Nombre d'heures passées devant la télévision par jour 0,89 0,83 – 0,95 <0,001
Pratique religieuse
    Pratiquant regulier — —
    Pratiquant occasionnel 0,99 0,68 – 1,43 >0,9
    Appartenance sans pratique 1,02 0,73 – 1,44 0,9
    Ni croyance ni appartenance 0,83 0,57 – 1,22 0,3
    Rejet 0,68 0,38 – 1,19 0,2
    NSP ou NVPR 0,93 0,40 – 2,04 0,9
Sexe * Groupe d'âges
    Homme * [25,45) 0,31 0,13 – 0,70 0,006
    Homme * [45,65) 0,24 0,10 – 0,54 <0,001
    Homme * [65,99] 0,23 0,09 – 0,59 0,003
1 OR = rapport de cotes, IC = intervalle de confiance

Commençons par regarder les effets du modèle.

plot(allEffects(mod2))
Représentation graphique des effets du modèle avec interaction entre le sexe et le groupe d’âge

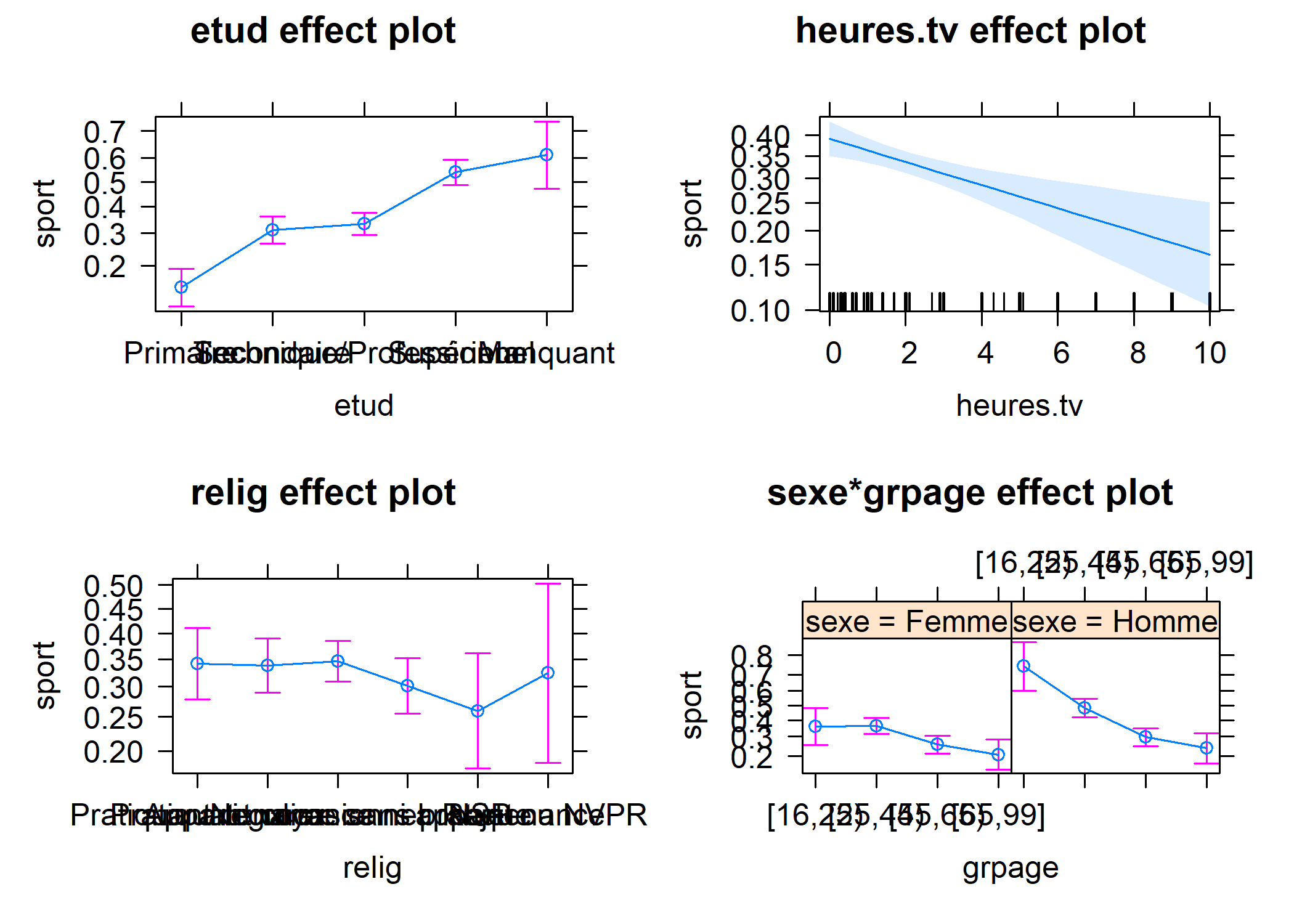
Sur ce graphique, on voit que l’effet de l’âge sur la pratique d’un sport est surtout marqué chez les hommes. Chez les femmes, le même effet est observé, mais dans une moindre mesure et seulement à partir de 45 ans.

On peut tester si l’ajout de l’interaction améliore significativement le modèle avec anova.

anova(mod2, test = "Chisq")

Jetons maintenant un oeil aux coefficients du modèle. Pour rendre les choses plus visuelles, nous aurons recours à ggcoef_model de l’extension GGally.

library(GGally)
ggcoef_model(mod2, exponentiate = TRUE)
Représentation graphique des coefficients du modèle avec interaction entre le sexe et le groupe d’âge

Concernant l’âge et le sexe, nous avons trois séries de coefficients : trois coefficients (grpage[25,45), grpage[45,65) et grpage[65,99]) qui correspondent à l’effet global de la variable âge, un coefficient (sexeHomme)pour l’effet global du sexe et trois coefficients qui sont des moficateurs de l’effet d’âge pour les hommes (grpage[25,45), grpage[45,65) et grpage[65,99]).

Pour bien interpréter ces coefficients, il faut toujours avoir en tête les modalités choisies comme référence pour chaque variable. Supposons une femme de 60 ans, dont toutes lautres variables correspondent aux modalités de référence (c’est donc une pratiquante régulière, de niveau primaire, qui ne regarde pas la télévision). Regardons ce que prédit le modèle quant à sa probabilité de faire du sport au travers d’une représentation graphique

library(breakDown)
library(ggplot2)
logit <- function(x) exp(x) / (1 + exp(x))
nouvelle_observation <- d[1, ]
nouvelle_observation$sexe[1] <- "Femme"
nouvelle_observation$grpage[1] <- "[45,65)"
nouvelle_observation$etud[1] <- "Primaire"
nouvelle_observation$relig[1] <- "Pratiquant regulier"
nouvelle_observation$heures.tv[1] <- 0
plot(
  broken(mod2, nouvelle_observation, predict.function = betas),
  trans = logit
) + ylim(0, 1) + ylab("Probabilité de faire du sport")
Scale for y is already present.
Adding another scale for y, which will replace the existing
scale.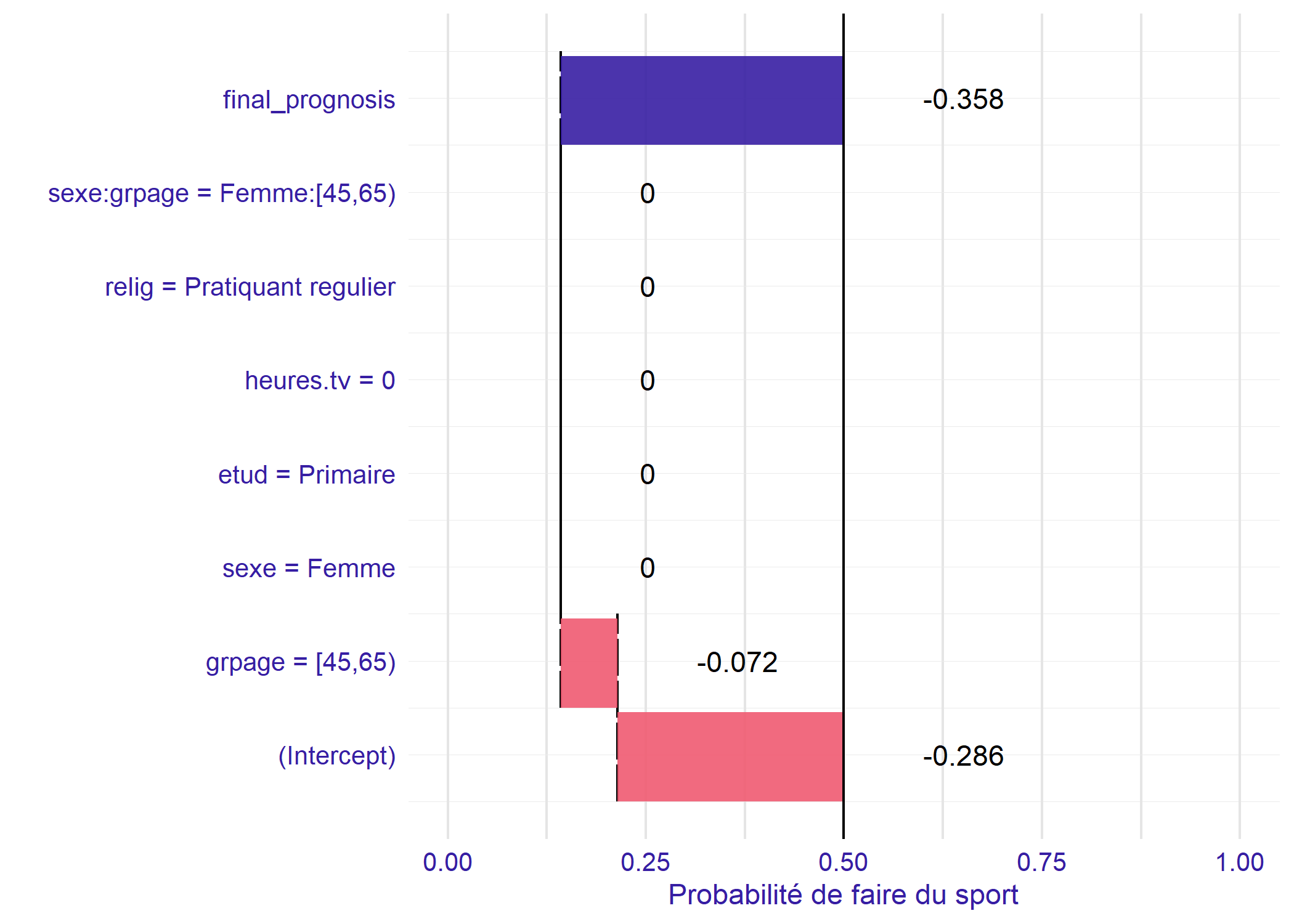
Représentation graphique de l’estimation de la probabilité de faire du sport pour une femme de 60 ans

En premier lieu, l’intercept s’applique et permet de déterminer la probabilité de base de faire du sport (si toutes les variables sont à leur valeur de référence). Femme étant la modalité de référence pour la variable sexe, cela ne modifie pas le calcul de la probabilité de faire du sport. Par contre, il y a une modification induite par la modalité 45-65 de la variable grpage.

Regardons maintenant la situation d’un homme de 20 ans.

nouvelle_observation$sexe[1] <- "Homme"
nouvelle_observation$grpage[1] <- "[16,25)"
plot(
  broken(mod2, nouvelle_observation, predict.function = betas),
  trans = logit
) + ylim(0, 1) + ylab("Probabilité de faire du sport")
Scale for y is already present.
Adding another scale for y, which will replace the existing
scale.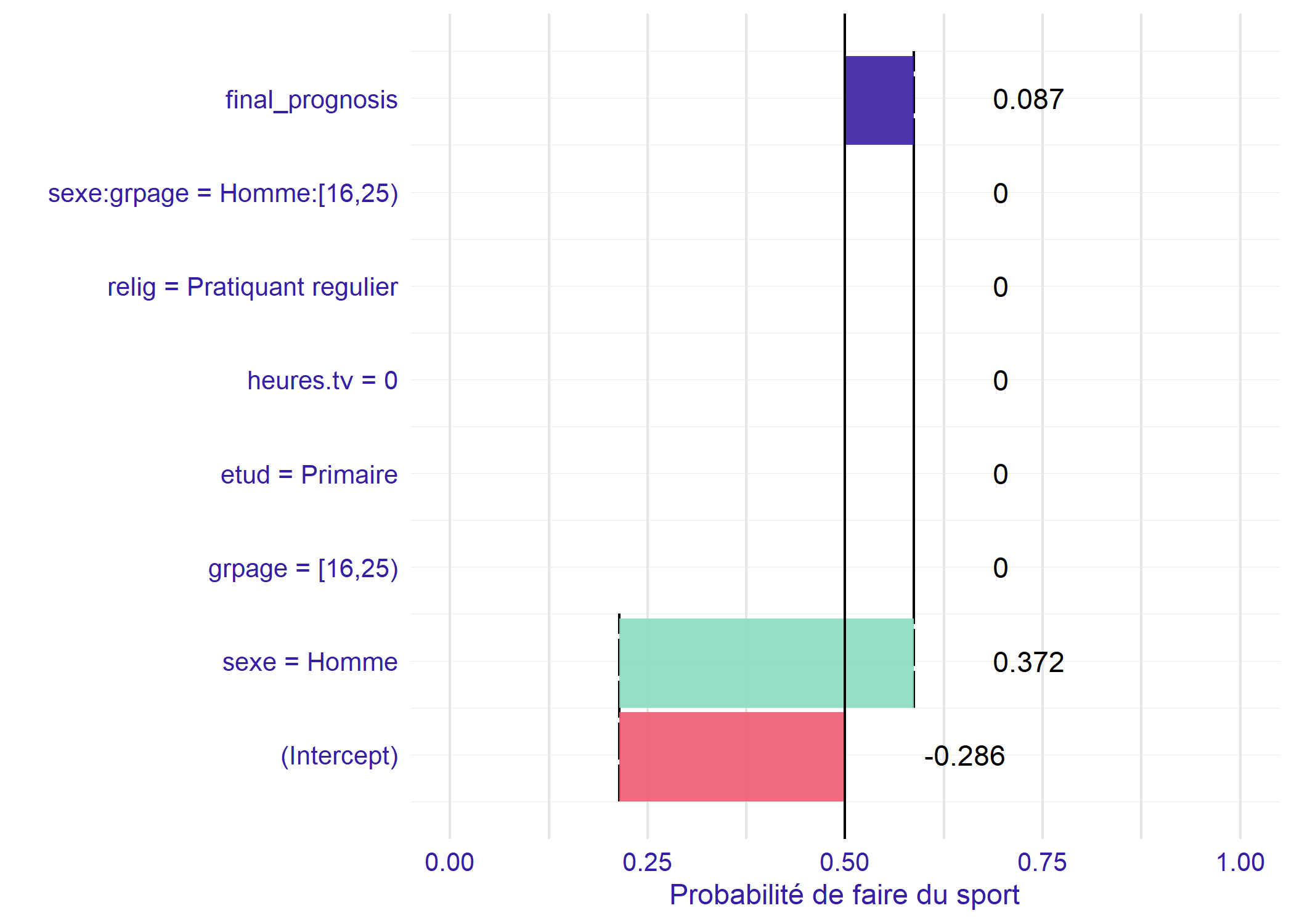
Représentation graphique de l’estimation de la probabilité de faire du sport pour un homme de 20 ans

Nous sommes à la modalité de référence pour l’âge par contre il y a un effet important du sexe. Le coefficient associé globalement à la variable sexe correspond donc à l’effet du sexe à la modalité de référence du groupe d’âges.

La situation est différente pour un homme de 60 ans.

nouvelle_observation$grpage[1] <- "[45,65)"
plot(
  broken(mod2, nouvelle_observation, predict.function = betas),
  trans = logit
) + ylim(0, 1) + ylab("Probabilité de faire du sport")
Scale for y is already present.
Adding another scale for y, which will replace the existing
scale.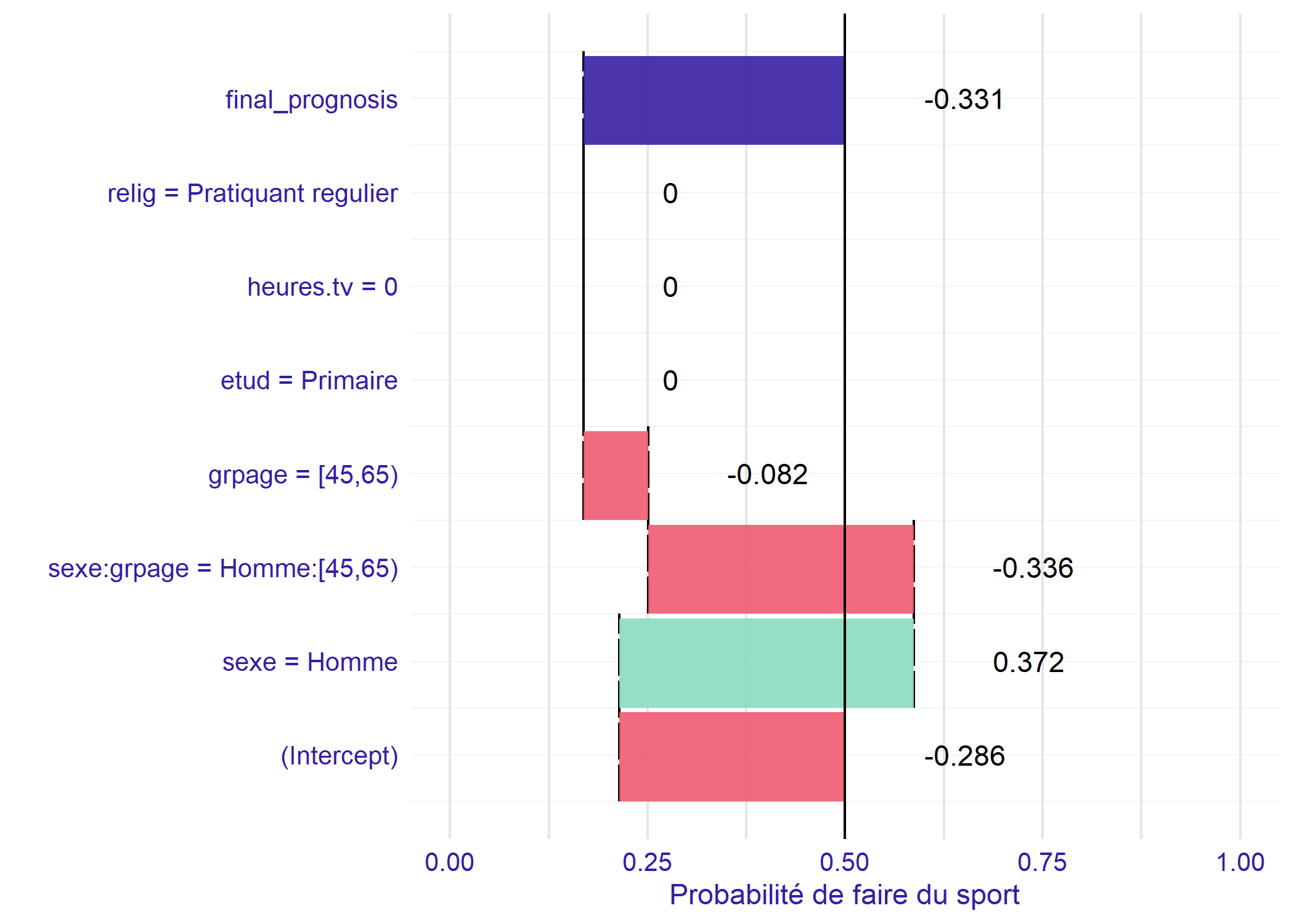
Représentation graphique de l’estimation de la probabilité de faire du sport pour un homme de 60 ans

Cette fois-ci, il y a plusieurs modifications d’effet. On applique en effet à la fois le coefficient sexe = Homme (effet du sexe pour les 15-24 ans), le coefficient grpage = [45-65) qui est l’effet de l’âge pour les femmes de 45-64 ans et le coefficient sexe:grpage = Homme:[45-65) qui indique l’effet spécifique qui s’applique aux hommes de 45-64, d’une part par rapport aux femmes du même et d’autre part par rapport aux hommes de 16-24 ans. L’effet des coefficients d’interaction doivent donc être interprétés par rapport aux autres coefficients du modèle qui s’appliquent, en tenant compte des modalités de référence.

Il est cependant possible d’écrire le même modèle différemment. En effet, sexe * grpage dans la formule du modèle est équivalent à l’écriture sexe + grpage + sexe:grpage, c’est-à-dire à modéliser un coefficient global pour chaque variable plus un des coefficients d’interaction. On aurait pu demander juste des coefficients d’interaction, en ne mettant que sexe:grpage.

mod3 <- glm(sport ~ sexe:grpage + etud + heures.tv + relig, data = d, family = binomial())
tbl_regression(mod3, exponentiate = TRUE)
Caractéristique OR1 95% IC1 p-valeur
Niveau d'étude
    Primaire — —
    Secondaire 2,60 1,77 – 3,85 <0,001
    Technique/Professionnel 2,88 1,99 – 4,21 <0,001
    Supérieur 6,77 4,64 – 10,0 <0,001
    Manquant 9,02 4,68 – 17,8 <0,001
Nombre d'heures passées devant la télévision par jour 0,89 0,83 – 0,95 <0,001
Pratique religieuse
    Pratiquant regulier — —
    Pratiquant occasionnel 0,99 0,68 – 1,43 >0,9
    Appartenance sans pratique 1,02 0,73 – 1,44 0,9
    Ni croyance ni appartenance 0,83 0,57 – 1,22 0,3
    Rejet 0,68 0,38 – 1,19 0,2
    NSP ou NVPR 0,93 0,40 – 2,04 0,9
Sexe * Groupe d'âges
    Femme * [16,25) 1,82 0,92 – 3,58 0,083
    Homme * [16,25) 9,46 4,34 – 21,8 <0,001
    Femme * [25,45) 1,86 1,17 – 3,00 0,009
    Homme * [25,45) 3,02 1,87 – 4,96 <0,001
    Femme * [45,65) 1,11 0,69 – 1,80 0,7
    Homme * [45,65) 1,35 0,84 – 2,21 0,2
    Femme * [65,99] 0,84 0,47 – 1,50 0,6
    Homme * [65,99]
1 OR = rapport de cotes, IC = intervalle de confiance

Au sens strict, ce modèle explique tout autant le phénomène étudié que le modèle précédent. On peut le vérifier facilement avec anova.

anova(mod2, mod3, test = "Chisq")

De même, les effets modélisés sont les mêmes.

plot(allEffects(mod3))
Représentation graphique des effets du modèle avec interaction simple entre le sexe et le groupe d’âge

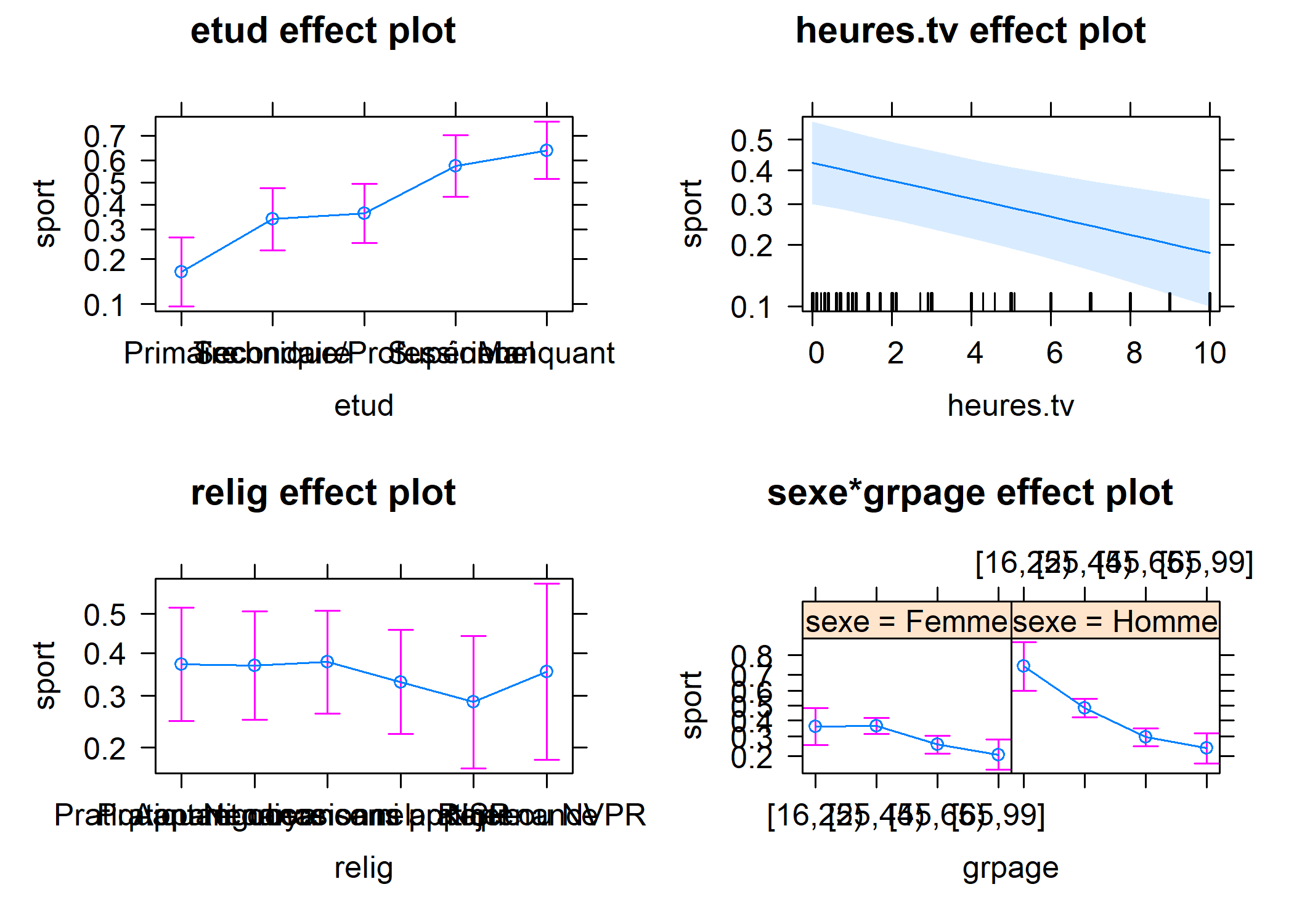
Par contre, regardons d’un peu plus près les coefficients de ce nouveau modèle. Nous allons voir que leur interprétation est légèrement différente.

ggcoef_model(mod3, exponentiate = TRUE)
Représentation graphique des coefficients du modèle avec interaction simple entre le sexe et le groupe d’âge

Cette fois-ci, il n’y a plus de coefficients globaux pour la variable sexe ni pour grpage mais des coefficients pour chaque combinaison de ces deux variables.

plot(
  broken(mod3, nouvelle_observation, predict.function = betas),
  trans = logit
) + ylim(0, 1) + ylab("Probabilité de faire du sport")
Scale for y is already present.
Adding another scale for y, which will replace the existing
scale.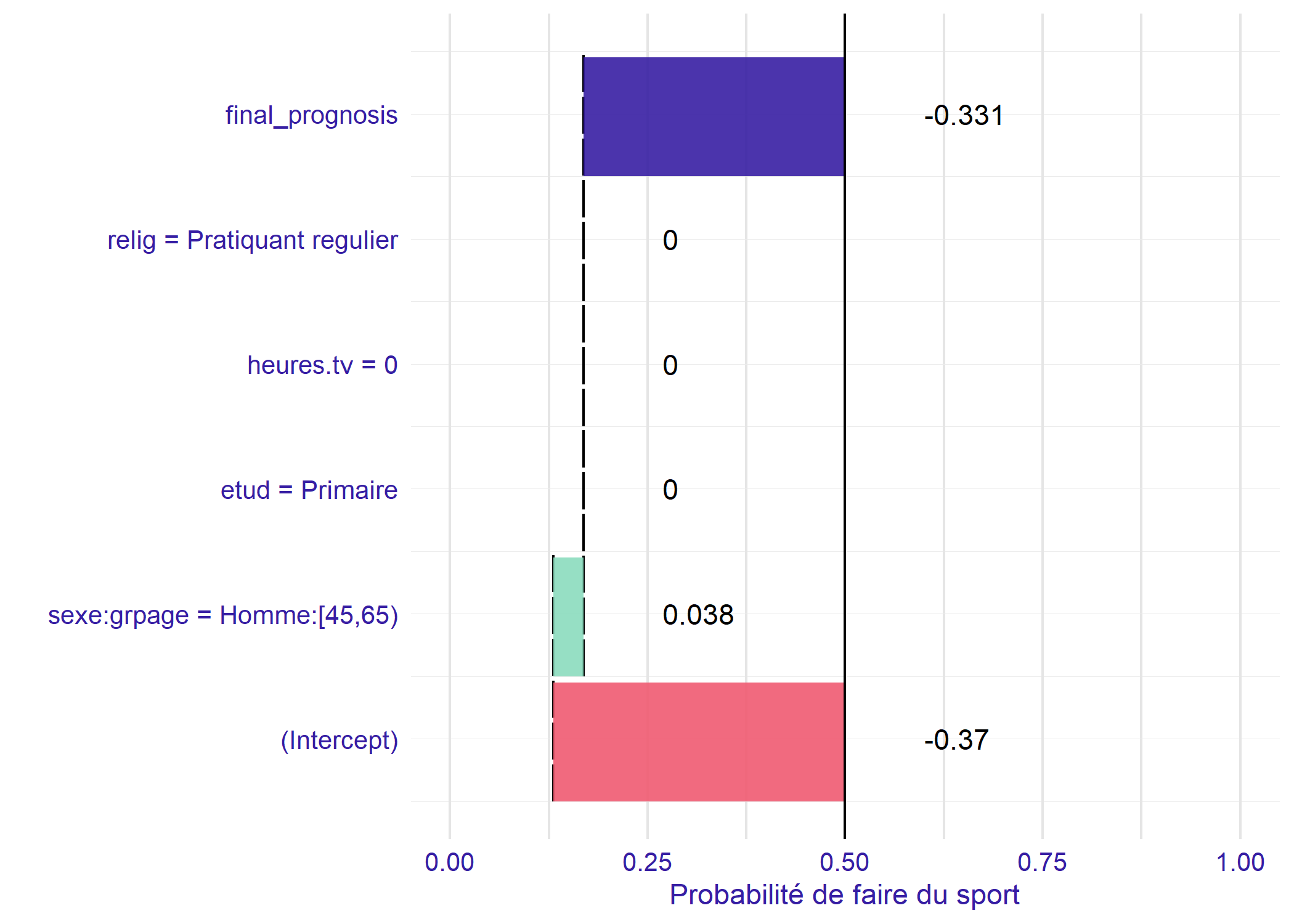
Représentation graphique de l’estimation de la probabilité de faire du sport pour un homme de 40 ans

Cette fois-ci, le coefficient d’interaction fourrnit l’effet global du sexe et de l’âge, et non plus la modification de cette combinaison par rapport aux coefficients globaux. Leur sens est donc différent et il faudra les interpréter en conséquence.

Un second exemple d’interaction

Intéressons-nous maintenant à l’interaction entre le sexe et le niveau d’étude. L’effet du niveau d’étude diffère-t-il selon le sexe ?

mod4 <- glm(sport ~ sexe * etud + grpage + heures.tv + relig, data = d, family = binomial())

Regardons d’abord les effets.

plot(allEffects(mod4))
Représentation graphique des effets du modèle avec interaction entre le sexe et le niveau d’étude

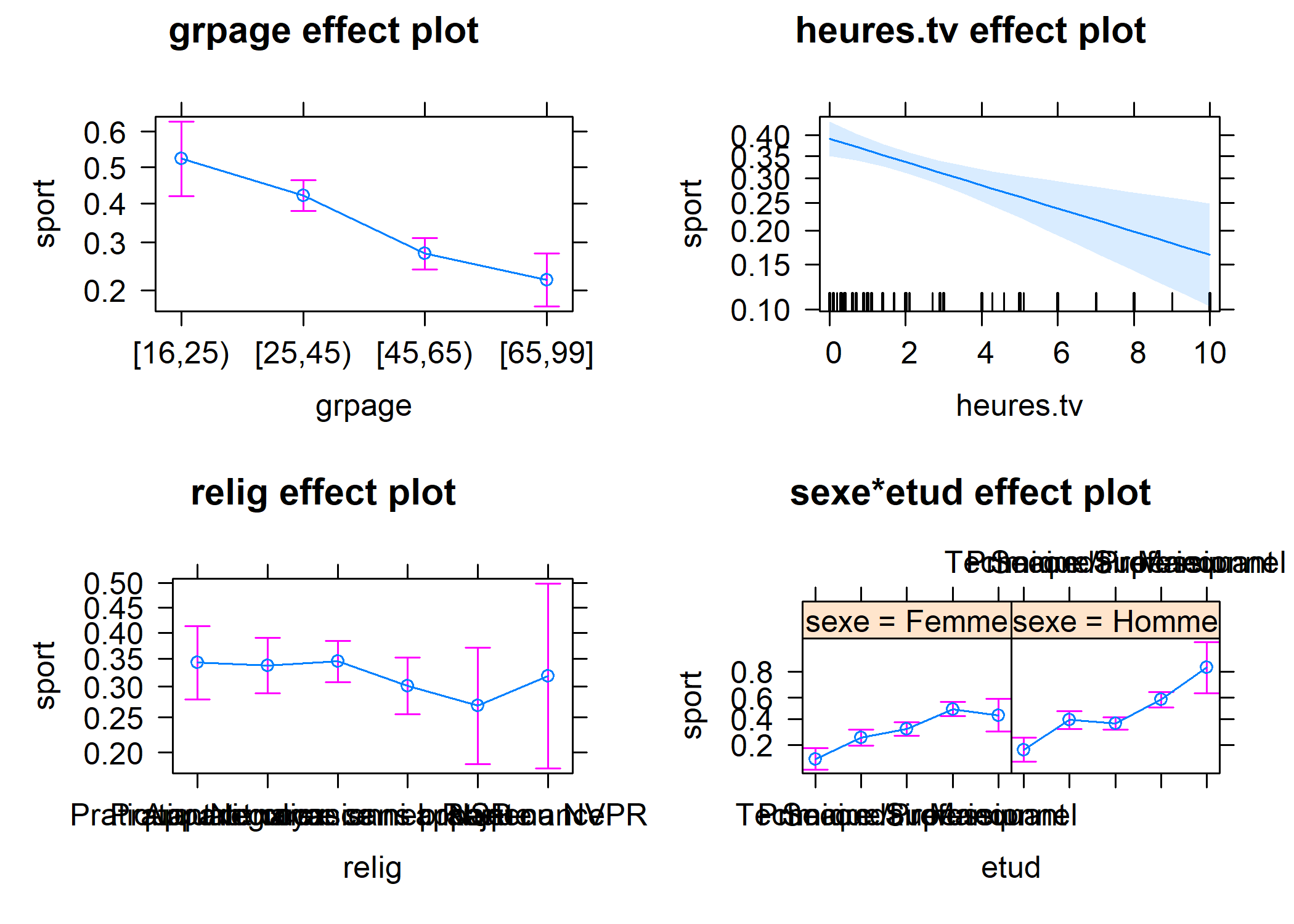
À première vue, l’effet du niveau d’étude semble être le même chez les hommes et chez les femmes. Ceci dit, cela serait peut être plus lisible si l’on superposait les deux sexe sur un même graphique. Nous allons utiliser la fonction ggeffect de l’extension ggeffects qui permets de récupérer les effets calculés avec effect dans un format utilisable avec ggplot2.

library(ggeffects)
plot(ggeffect(mod4, c("etud", "sexe")))
Effets du niveau d’étude selon le sexe

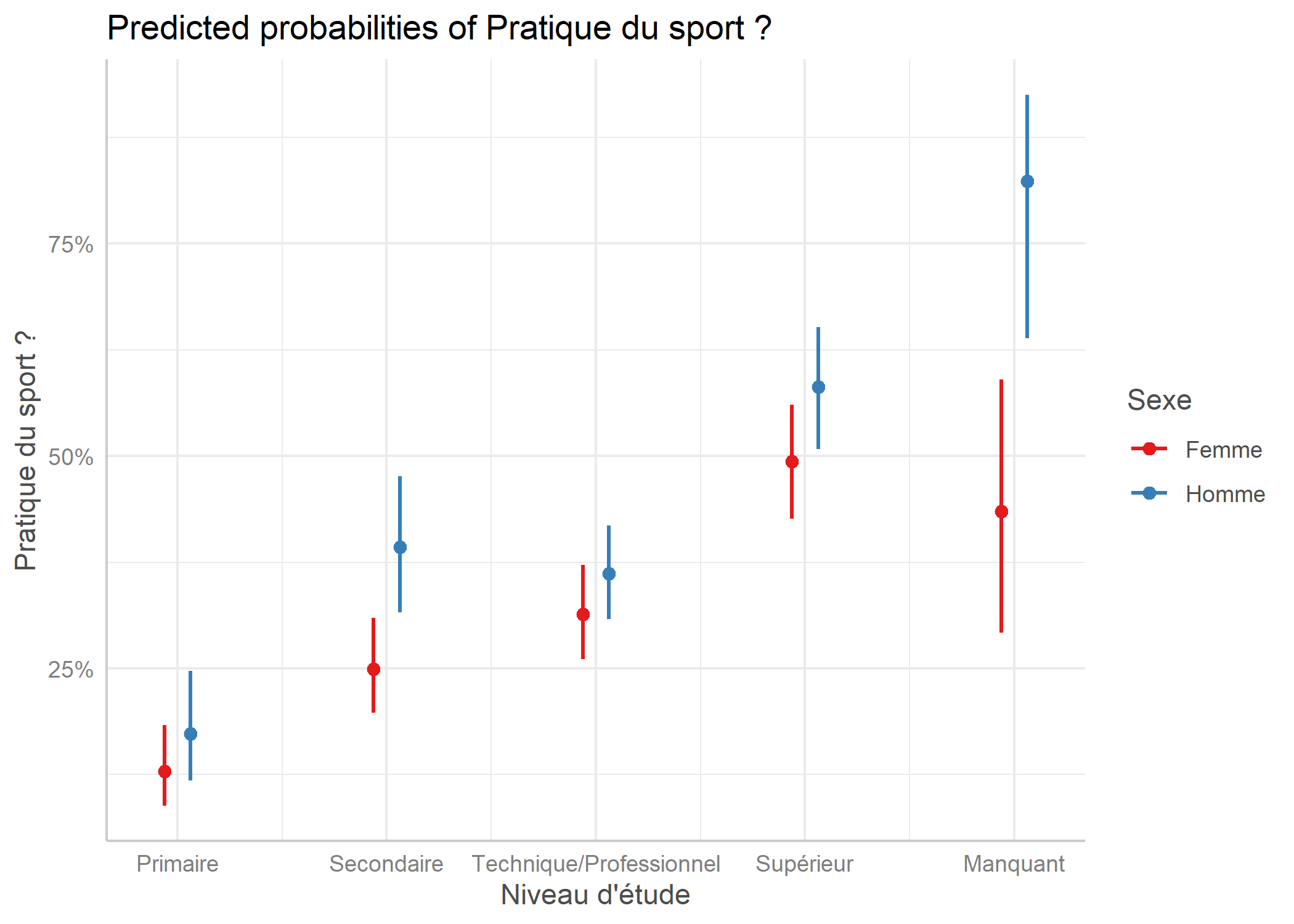
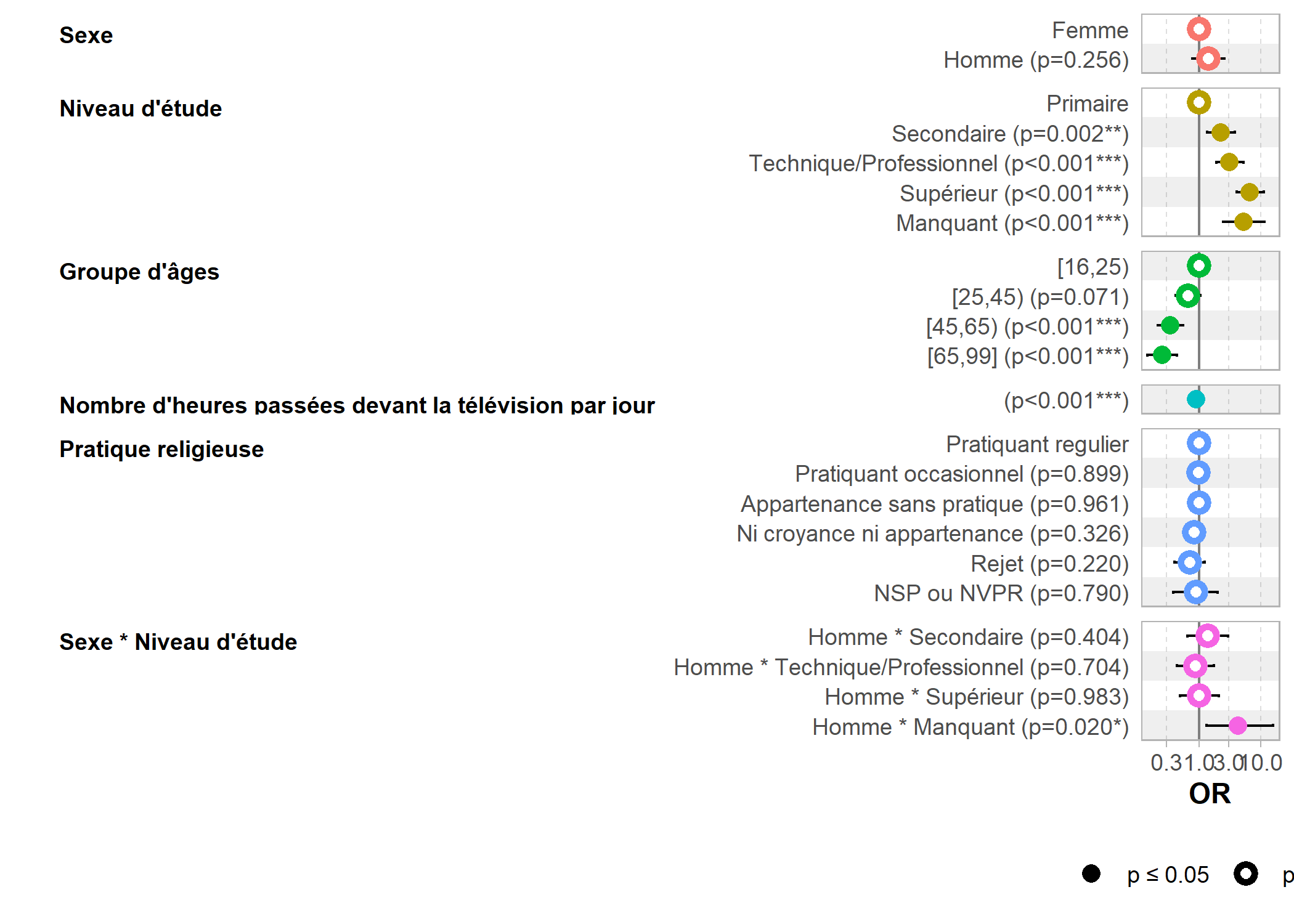
Cela confirme ce que l’on suppose. Regardons les coefficients du modèle.

ggcoef_model(mod4, exponentiate = TRUE)
Représentation graphique des coefficients du modèle avec interaction simple entre le sexe et le niveau d’étude 
tbl_regression(mod4, exponentiate = TRUE)
Caractéristique OR1 95% IC1 p-valeur
Sexe
    Femme — —
    Homme 1,42 0,77 – 2,58 0,3
Niveau d'étude
    Primaire — —
    Secondaire 2,25 1,35 – 3,82 0,002
    Technique/Professionnel 3,09 1,90 – 5,17 <0,001
    Supérieur 6,59 4,02 – 11,1 <0,001
    Manquant 5,21 2,42 – 11,4 <0,001
Groupe d'âges
    [16,25) — —
    [25,45) 0,66 0,42 – 1,04 0,071
    [45,65) 0,34 0,21 – 0,55 <0,001
    [65,99] 0,25 0,15 – 0,43 <0,001
Nombre d'heures passées devant la télévision par jour 0,89 0,83 – 0,95 <0,001
Pratique religieuse
    Pratiquant regulier — —
    Pratiquant occasionnel 0,98 0,67 – 1,42 0,9
    Appartenance sans pratique 1,01 0,72 – 1,43 >0,9
    Ni croyance ni appartenance 0,83 0,56 – 1,21 0,3
    Rejet 0,70 0,40 – 1,23 0,2
    NSP ou NVPR 0,90 0,39 – 1,98 0,8
Sexe * Niveau d'étude
    Homme * Secondaire 1,38 0,65 – 2,93 0,4
    Homme * Technique/Professionnel 0,87 0,44 – 1,75 0,7
    Homme * Supérieur 1,01 0,49 – 2,07 >0,9
    Homme * Manquant 4,28 1,32 – 15,8 0,020
1 OR = rapport de cotes, IC = intervalle de confiance

Si les coefficients associés au niveau d’étude sont significatifs, ceux de l’interaction ne le sont pas (sauf sexeHomme:etudManquant) et celui associé au sexe, précédemment significatif ne l’est plus. Testons avec anova si l’interaction est belle et bien significative.

anova(mod4, test = "Chisq")

L’interaction est bien significative mais faiblement. Vu que l’effet du niveau d’étude reste nénamoins très similaire selon le sexe, on peut se demander s’il est pertinent de la conserver.

Explorer les différentes interactions possibles

Il peut y avoir de multiples interactions dans un modèle, d’ordre 2 (entre deux variables) ou plus (entre trois variables ou plus). Il est dès lors tentant de tester les multiples interactions possibles de manière itératives afin d’identifier celles à retenir. C’est justement le but de la fonction glmulti de l’extension du même nom. glmulti permets de tester toutes les combinaisons d’interactions d’ordre 2 dans un modèle, en retenant le meilleur modèle à partir d’un critère spécifié (par défaut l’AIC). ATTENTION : le temps de calcul de glmulti peut-être long.

library(glmulti)
glmulti(sport ~ sexe + grpage + etud + heures.tv + relig, data = d, family = binomial())
Initialization...
TASK: Exhaustive screening of candidate set.
Fitting...

After 50 models:
Best model: sport~1+grpage+heures.tv+sexe:heures.tv+grpage:heures.tv+etud:heures.tv
Crit= 2284.87861987263
Mean crit= 2406.80086471225

After 100 models:
Best model: sport~1+etud+heures.tv+grpage:heures.tv
Crit= 2267.79462883348
Mean crit= 2360.46497457747

After 150 models:
Best model: sport~1+grpage+etud+heures.tv+sexe:heures.tv
Crit= 2228.88574082404
Mean crit= 2286.60589884071

After 200 models:
Best model: sport~1+grpage+etud+heures.tv+sexe:heures.tv
Crit= 2228.88574082404
Mean crit= 2254.99359340075

After 250 models:
Best model: sport~1+sexe+grpage+etud+heures.tv+etud:sexe+sexe:heures.tv
Crit= 2226.00088609349
Mean crit= 2241.76611580481

After 300 models:
Best model: sport~1+sexe+grpage+etud+heures.tv+grpage:sexe+sexe:heures.tv
Crit= 2222.67161519005
Mean crit= 2234.95020358944

On voit qu’au bout d’un moment, l’algorithme se statibilise autour d’un modèle comportant une interaction entre le sexe et l’âge d’une part et entre le sexe et le nombre d’heures passées quotidiennement devant la télé. On voit également que la variable religion a été retirée du modèle final.

best <- glm(sport ~ 1 + sexe + grpage + etud + heures.tv + grpage:sexe + sexe:heures.tv, data = d, family = binomial())
odds.ratio(best)
Attente de la réalisation du profilage...
ggcoef_model(best, exponentiate = TRUE)
Représentation graphique des coefficients du modèle avec interaction entre le sexe, le niveau d’étude et le nombre d’heures passées devant la télévision 
plot(allEffects(best))
Représentation graphique des effets du modèle avec interaction entre le sexe, le niveau d’étude et le nombre d’heures passées devant la télévision

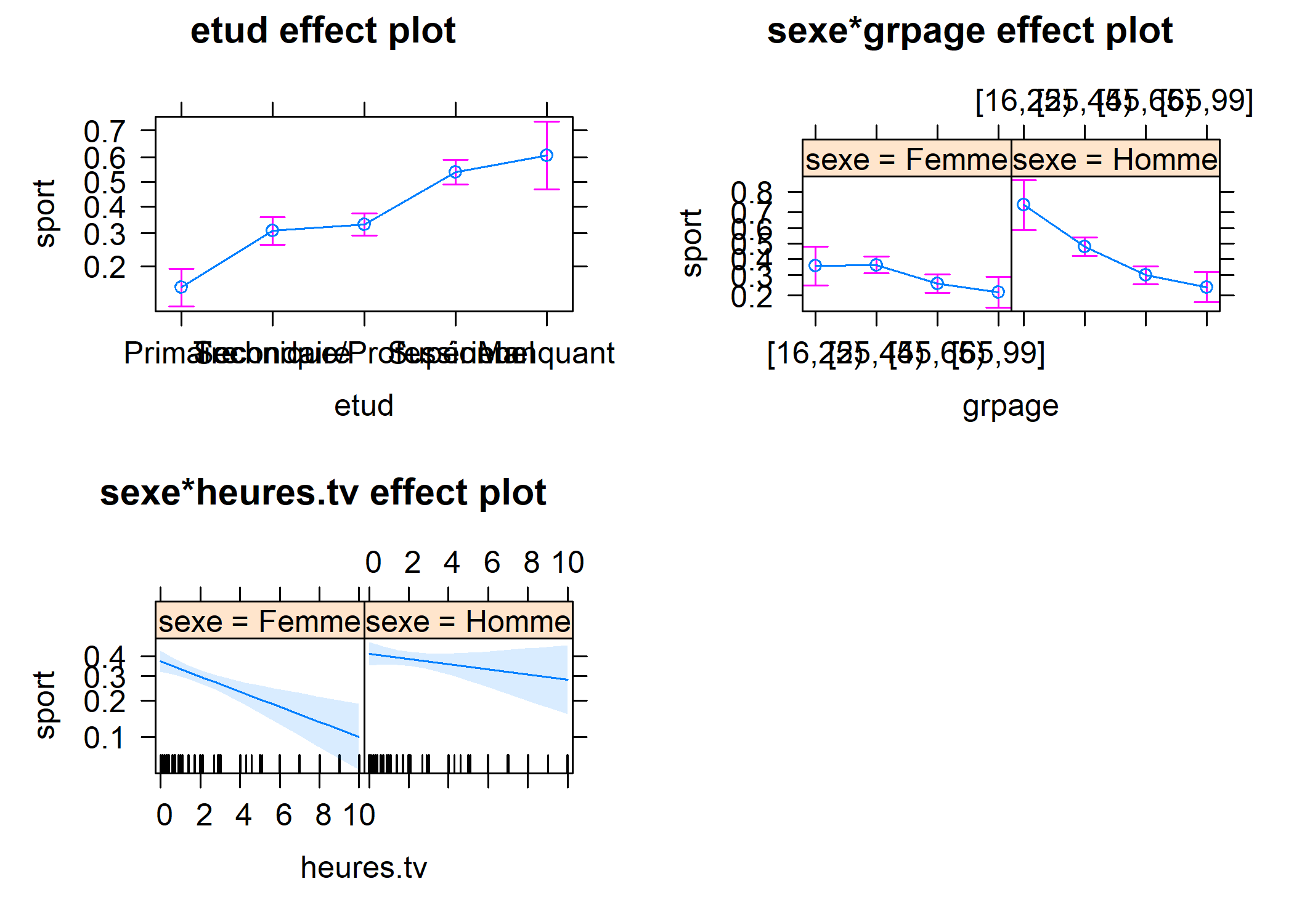
Pour aller plus loin

Il y a d’autres extensions dédiées à l’analyse des interactions d’un modèle, de même que de nombreux supports de cours en ligne dédiés à cette question.

On pourra en particulier se référer à la vignette inclue avec l’extension phia : https://cran.r-project.org/web/packages/phia/vignettes/phia.pdf.

  1. Pour une présentation plus statistique et mathématique des effets d’interaction, on pourra se référer au cours de Jean-François Bickel disponible en ligne.↩︎