Une version actualisée de ce chapitre est disponible sur guide-R : Graphiques avec ggplot2

Ce chapitre est tiré d’une séance de cours de François Briatte et destinée à des étudiants de L2 sans aucune connaissance de R. Cette séance de cours est elle-même inspirée d’un exercice tiré d’un cours de Cosma Shalizi.

Ce chapitre est évoqué dans le webin-R #08 (ggplot2 et la grammaires des graphiques) sur YouTube.

R possède un puissant moteur graphique interne, qui permet de dessiner dans un graphique en y rajoutant des segments, des points, du texte, ou toutes sortes d’autres symboles. Toutefois, pour produire un graphique complet avec les fonctions basiques de R, il faut un peu bricoler : d’abord, ouvrir une fenêtre ; puis rajouter des points ; puis rajouter des lignes ; tout en configurant les couleurs au fur-et-à-mesure ; puis finir par fermer la fenêtre graphique.

L’extension ggplot21, développée par Hadley Wickham et mettant en œuvre la grammaire graphique théorisée par Leland Wilkinson, devient vite indispensable lorsque l’on souhaite réaliser des graphiques plus complexes2. On renvoit le lecteur intéressé à l’ouvrage de Winston Chang, R Graphics Cookbook, disponible gratuitement dans sa deuxième édition à l’adresse suivante : https://r-graphics.org.

Ce chapitre, articulé autour d’une étude de cas, présente ggplot2 à partir d’un exemple simple de visualisation de séries temporelles, puis rentre dans le détail de sa syntaxe. Pour une présentation plus formelle, on pourra se référer au chapitre dédié de la section Approfondir.

Les données de l’exemple

Il y a quelques années, les chercheurs Carmen M. Reinhart et Kenneth S. Rogoff publiaient un article intitulé Growth in a Time of Debt, dans lequel ils faisaient la démonstration qu’un niveau élevé de dette publique nuisait à la croissance économique. Plus exactement, les deux chercheurs y défendaient l’idée que, lorsque la dette publique dépasse 90 % du produit intérieur brut, ce produit cesse de croître.

Cette conclusion, proche du discours porté par des institutions comme le Fonds Monétaire International, a alimenté plusieurs argumentaires politiques. Des parlementaires américains s’en ainsi sont servi pour exiger une diminution du budget fédéral, et surtout, la Commission européenne s’est appuyée sur cet argumentaire pour exiger que des pays comme la Grèce, durement frappés par la crise financière globale de 2008, adoptent des plans d’austérité drastiques.

Or, en tentant de reproduire les résultats de Reinhart et Rogoff, les chercheurs Thomas Herndon, Michael Ash et Robert Pollin y ont trouvé de nombreuses erreurs, ainsi qu’une bête erreur de calcul due à une utilisation peu attentive du logiciel Microsoft Excel. La révélation de ces erreurs donna lieu à un débat très vif entre adversaires et partisans des politiques économiques d’austérité, débat toujours autant d’actualité aujourd’hui.

Dans ce chapitre, on va se servir des données (corrigées) de Reinhart et Rogoff pour évaluer, de manière indépendante, la cohérence de leur argument sur le rapport entre endettement et croissance économique. Commençons par récupérer ces données au format CSV sur le site du chercheur américain Cosma Shalizi, qui utilise ces données dans l’un de ses exercices de cours :

# charger l'extension lisant le format CSV
library(readr)

# emplacement souhaité pour le jeu de données
file <- "data/debt.csv"

# télécharger le jeu de données s'il n'existe pas
if(!file.exists(file))
  download.file("http://www.stat.cmu.edu/~cshalizi/uADA/13/hw/11/debt.csv",
                file, mode = "wb")

# charger les données dans l'objet 'debt'
debt <- read_csv(file)
New names:
Rows: 1171 Columns: 5
── Column specification
──────────────────────────────────── Delimiter: "," chr
(1): Country dbl (4): ...1, Year, growth, ratio
ℹ Use `spec()` to retrieve the full column specification
for this data. ℹ Specify the column types or set
`show_col_types = FALSE` to quiet this message.
• `` -> `...1`

Le code ci-dessus utilise la fonction read_csv de l’extension readr, dont on a recommandé l’utilisation dans un précédent chapitre. En l’absence de cette extension, on aurait pu utiliser la fonction de base read.csv.

Nettoyage des données

Les données de Reinhart et Rogoff contiennent, pour un échantillon de 20 pays occidentaux membres de la zone OCDE, la croissance de leur produit intérieur brut (PIB)3, et le ratio entre leur dette publique et ce produit, exprimé sous la forme d’un pourcentage Dette / PIB. Les données vont du milieu des années 1940 à la fin des années 2000. La première colonne du jeu de données ne contenant que les numéros des lignes, on va la supprimer d’entrée de jeu :

# inspection du jeu de données
str(debt)
spc_tbl_ [1,171 × 5] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
 $ ...1   : num [1:1171] 147 148 149 150 151 152 153 154 155 156 ...
 $ Country: chr [1:1171] "Australia" "Australia" "Australia" "Australia" ...
 $ Year   : num [1:1171] 1946 1947 1948 1949 1950 ...
 $ growth : num [1:1171] -3.56 2.46 6.44 6.61 6.92 ...
 $ ratio  : num [1:1171] 190 177 149 126 110 ...
 - attr(*, "spec")=
  .. cols(
  ..   ...1 = col_double(),
  ..   Country = col_character(),
  ..   Year = col_double(),
  ..   growth = col_double(),
  ..   ratio = col_double()
  .. )
 - attr(*, "problems")=<externalptr> 
# suppression de la première colonne
debt <- debt[, -1]

Il faut aussi noter d’emblée que certaines mesures sont manquantes : pour certains pays, on ne dispose pas d’une mesure fiable du PIB et/ou de la dette publique. En conséquence, le nombre d’observations par pays est différent, et va de 40 observations pays-année pour la Grèce à 64 observations pays-année pour plusieurs pays comme l’Australie ou les États-Unis :

table(debt$Country)

  Australia     Austria     Belgium      Canada     Denmark 
         64          59          63          64          56 
    Finland      France     Germany      Greece     Ireland 
         64          54          59          40          63 
      Italy       Japan Netherlands New Zealand      Norway 
         59          54          53          64          64 
   Portugal       Spain      Sweden          UK          US 
         58          42          64          63          64

Recodage d’une variable

Dernière manipulation préalable avant l’analyse : on va calculer la décennie de chaque observation, en divisant l’année de mesure par 10, et en multipliant la partie entière de ce résultat par 10. Cette manipulation très simple donne 1940 pour les mesures des années 1940 à 1949, 1950 pour les années 1950-1959, et ainsi de suite.

debt$Decade <- factor(10 * debt$Year %/% 10)

Voici, pour terminer, les premières lignes du jeu de données sur lequel on travaille :

head(debt)

Visualisation des données

Chargeons à présent l’extension graphique ggplot2 :

library(ggplot2)

Procédons désormais à quelques visualisations très simples de ces données. On dispose de trois variables continues : l’année, le taux de croissance du PIB, et le ratio Dette publique / PIB. Si l’on souhaite visualiser la croissance du PIB au cours du temps, la solution basique dans R s’écrit de la manière suivante :

with(debt, plot(Year, growth))

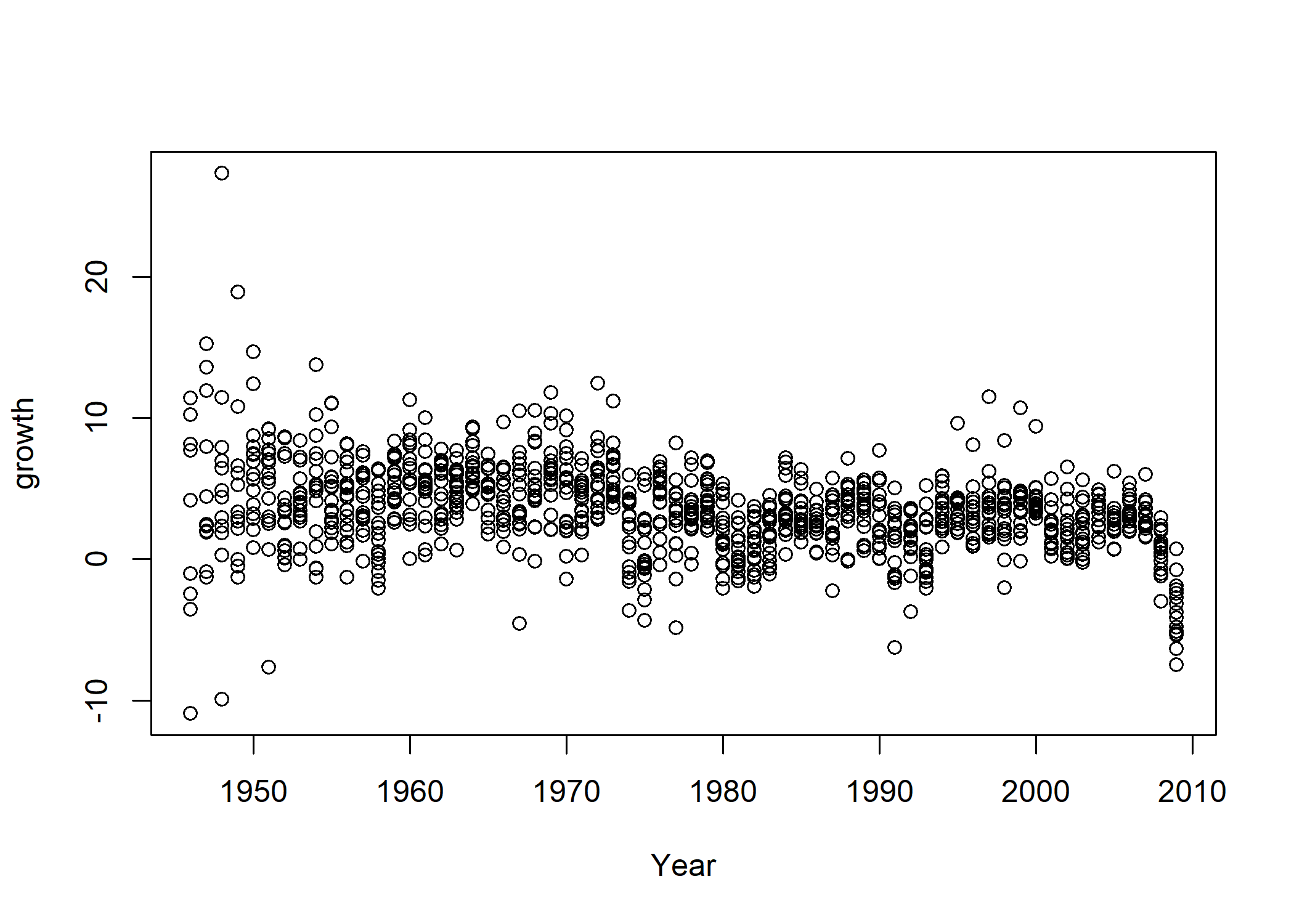
Le code de la visualisation est très simple et se lit : avec l’objet debt, construire le graphique montrant l’année d’observation Year en abcisse et le taux de croissance du PIB growth en ordonnée. Le code est compris de cette manière par R car la fonction plot comprend le premier argument comme étant la variable à représenter sur l’axe horizontal x, et le second comme la variable à représenter sur l’axe vertical y.

Le même graphique s’écrit de la manière suivante avec l’extension ggplot2 :

with(debt, qplot(Year, growth))

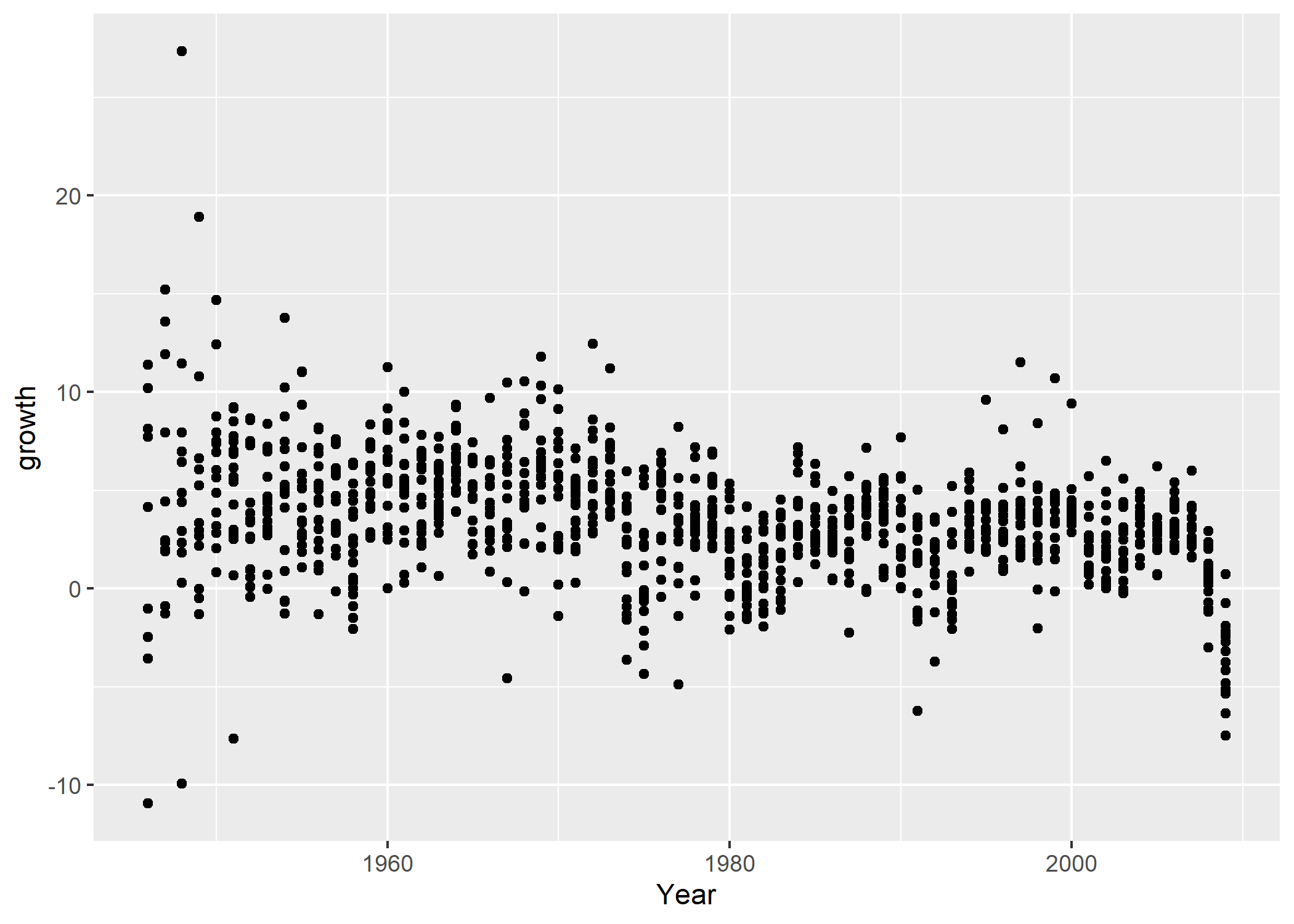
Comme on peut le voir, le code est très proche du code utilisé dans R base, la syntaxe signifiant toujours : avec le jeu de données debt, visualiser les variables Year sur l’axe x et growth sur l’axe y. Le résultat est similaire, bien que plusieurs paramètres graphiques aient changé : le fond gris clair, en particulier, est caractéristique du thème graphique par défaut de ggplot2, que l’on apprendra à modifier plus loin.

Par ailleurs, dans les deux exemples précédents, on a écrit with(debt, ...) pour indiquer que l’on travaillait avec l’objet debt. Lorsque l’on travaille avec l’extension ggplot2, il est toutefois plus commun d’utiliser l’argument data dans l’appel de qplot pour indiquer ce choix :

qplot(Year, growth, data = debt)

Visualisation par petits multiples

Cherchons désormais à mieux comprendre les variations du taux de croissance du PIB au fil des années.

Dans les graphiques précédents, on voit clairement que ce taux est très variable dans l’immédiat après-guerre, puis qu’il oscille entre environ -5 % et +15 %, puis qu’il semble chuter dramatiquement à la fin des années 2000, marquées par la crise financière globale. Mais comment visualiser ces variations pour chacun des vingt pays de l’échantillon ?

On va ici utiliser le principe de la visualisation par petits multiples, c’est-à-dire que l’on va reproduire le même graphique pour chacun des pays, et visualiser l’ensemble de ces graphiques dans une même fenêtre. Concrètement, il va donc s’agir de montrer la croissance annuelle du PIB en faisant apparaître chaque pays dans une facette différente du graphique.

ggplot2 permet d’effectuer cette opération en rajoutant au graphique précédent, au moyen de l’opérateur +, l’élément facet_wrap(~ Country) au graphique et qui signifie construire le graphique pour chaque valeur différente de la variable Country. On notera que la fonction facet_wrap utilise la syntaxe équation de R. Par défaut, ces facettes sont classées par ordre alphabétique :

qplot(Year, growth, data = debt) +
  facet_wrap(~ Country)

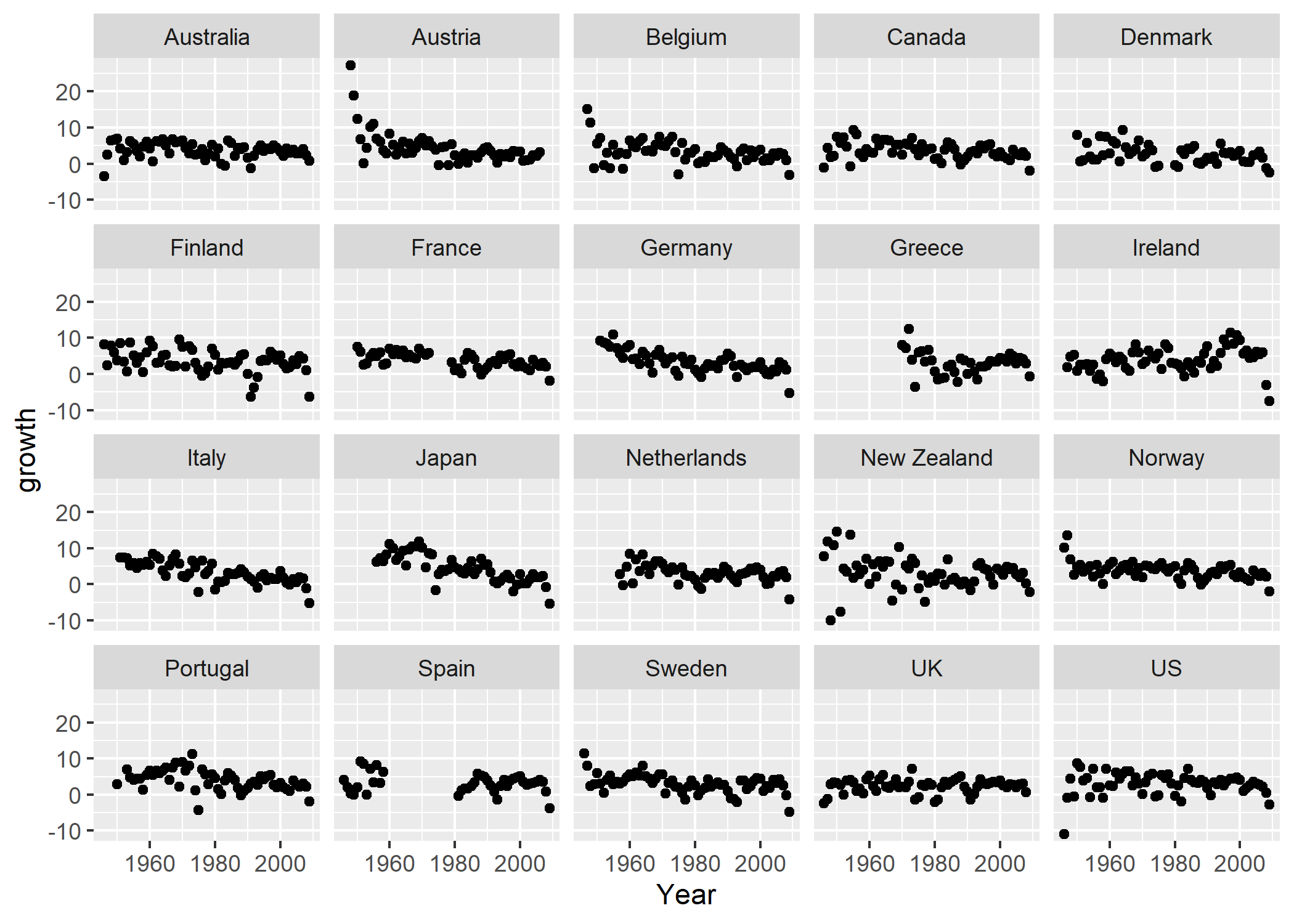
Voilà qui est beaucoup plus clair ! On aperçoit bien, dans ce graphique, les variations très importantes de croissance du PIB dans un pays comme l’Autriche, ruinée après la Seconde guerre mondiale, ou l’Irlande, très durement frappée par la crise financière globale en 2008 et 2009. On aperçoit aussi où se trouvent les données manquantes : voir le graphique de l’Espagne, par exemple.

Il faut noter ici un élément essentiel de la grammaire graphique de ggplot2, qui utilise une syntaxe additive, où différents éléments et paramètres graphiques peuvent être combinés en les additionnant, ce qui permet de construire et de modifier des graphiques de manière cumulative, pas à pas. Cette caractéristique permet de tâtonner, et de construire progressivement des graphiques très complets.

Visualisation en séries temporelles

Enfin, pour produire le même graphique que ci-dessus en utilisant des lignes plutôt que des points, il suffit d’utiliser l’argument geom = "line", ce qui peut être considéré comme une meilleure manière de visualiser des séries temporelles, mais qui tend aussi à rendre plus difficile la détection des périodes pour lesquelles il manque des données (voir, à nouveau, le graphique pour l’Espagne) :

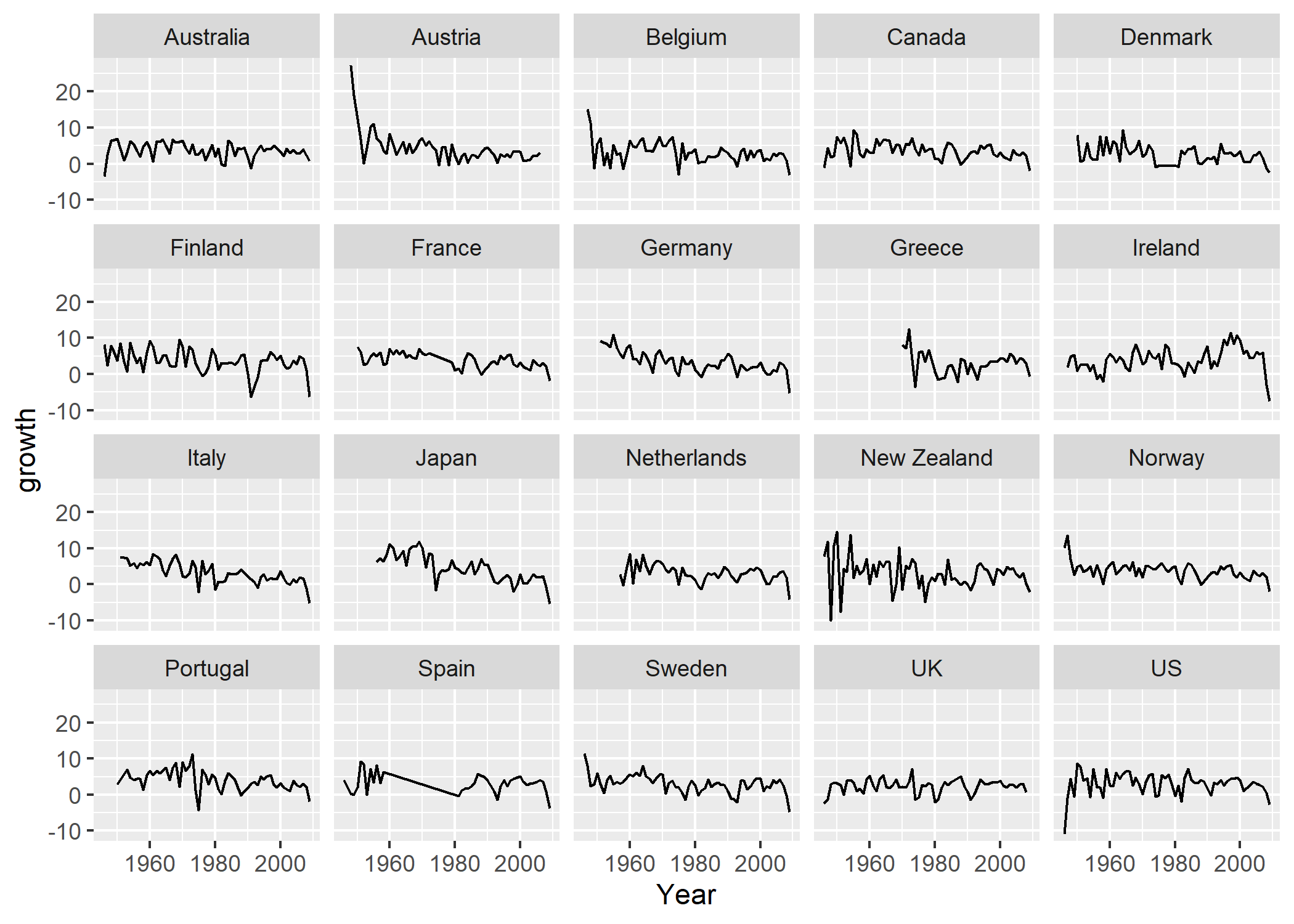
qplot(data = debt, y = growth, x = Year, geom = "line") + 
  facet_wrap(~ Country)

Dans ce dernier exemple, on a défini l’axe y avant de définir l’axe x, en écrivant ces arguments de manière explicite ; de même, on a commencé par spécifier l’argument data, et l’on a terminé par l’argument geom. Cet ordre d’écriture permet de conserver une forme de cohérence dans l’écriture des fonctions graphiques.

Combinaisons d’éléments graphiques

On n’a pas encore visualisé le ratio Dette publique / PIB, l’autre variable du raisonnement de Reinhart et Rogoff. C’est l’occasion de voir comment rajouter des titres aux axes des graphiques, et d’utiliser les lignes en même temps que des points, toujours grâce à l’argument geom, qui peut prendre plusieurs valeurs (ici, "point" produit les points et "line" produit les lignes) :

qplot(data = debt, y = ratio, x = Year, geom = c("line", "point")) + 
  facet_wrap(~ Country) +
  labs(x = NULL,
       y = "Ratio dette publique / produit intérieur brut (%)")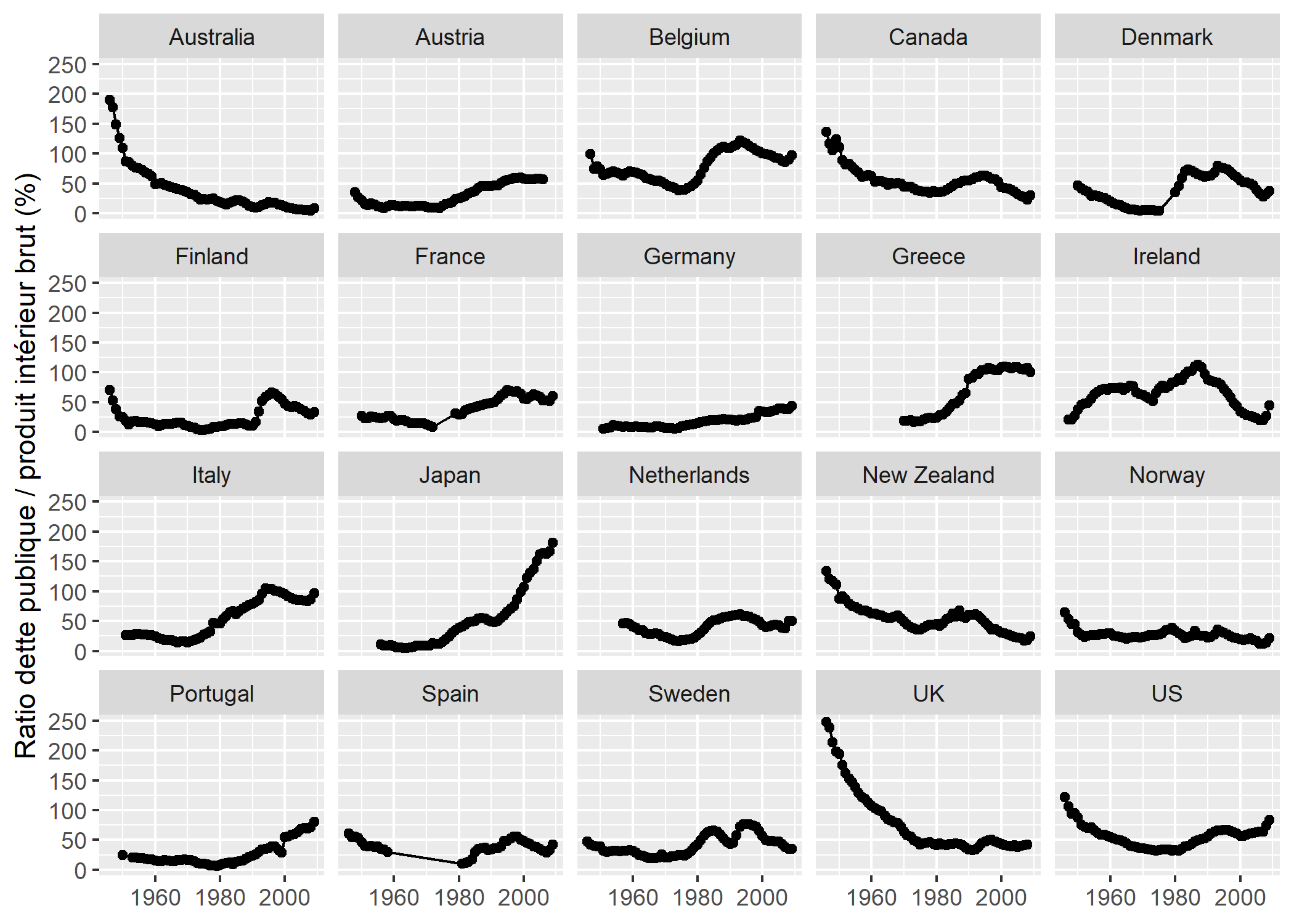

Dans ce graphique, on a combiné deux objets géométriques (geom) pour afficher à la fois des points et des lignes. On a ensuite défini les titres des axes, en supprimant celui de l’axe x, et en rajoutant un peu d’espace entre le titre de l’axe y et l’axe lui-même grâce à la chaîne de caractères finale \n, qui rajoute une ligne vide entre ces deux éléments4.

Les différents exemples vus dans cette section montrent qu’il va falloir apprendre un minimum de syntaxe graphique pour parvenir à produire des graphiques avec ggplot2. Ce petit investissement permet de savoir très vite produire de très nombreux types de graphiques, assez élégants de surcroît, et très facilement modifiables à l’aide de toutes sortes de paramètres optionnels.

Aussi élégants que soient vos graphiques, il ne vous dispense évidemment pas de réfléchir à ce que vous êtes en train de visualiser, un graphique très élégant pouvant naturellement être complètement erroné, en particulier si les données de base du graphique ont été mal mesurées… ou endommagées.

Composition graphique avec ggplot2

La section précédente a montré comment utiliser la fonction qplot (quick plot). La syntaxe complète de l’extension ggplot2 passe par une autre fonction, ggplot, qui permet de mieux comprendre les différents éléments de sa grammaire graphique. Dans cette section, on va détailler cette syntaxe pour en tirer un graphique plus complexe que les précédents.

Commençons par créer un treillis de base au graphique :

p <- ggplot(data = debt, aes(y = growth, x = ratio))

Aucun graphique ne s’affiche ici : en effet, ce que l’on a stocké, dans l’objet p, n’est pas un graphique complet, mais une base de travail. Cette base définit les coordonnées x et y du graphique dans l’argument aes (aesthetics). Ici, on a choisi de mettre la variable dépendante de Reinhart et Rogoff, growth (le taux de croissance du PIB), sur l’axe y, et la variable indépendante ratio (le ratio Dette publique / PIB) sur l’axe x.

Rajoutons désormais un objet géométrique, geom_point, qui va projeter, sur le graphique, des points aux coordonnées précédemment définies, et divisons le graphique par un petit multiple, en projetant les points de chaque décennie dans une facette différente du graphique. Ce graphique propose une décomposition temporelle de la relation étudiée par Reinhart et Rogoff :

p + geom_point() +
  facet_grid(. ~ Decade)

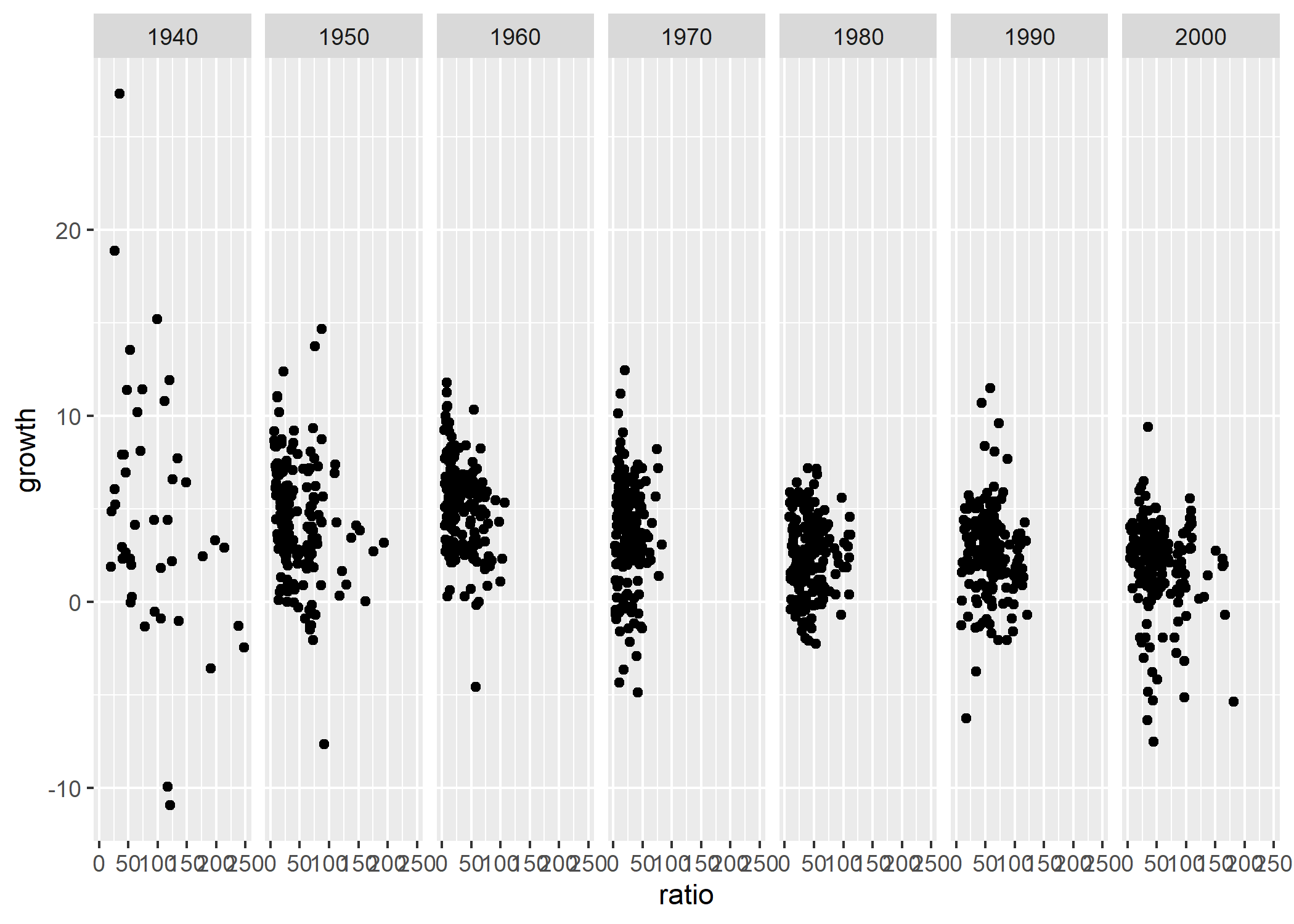
Le paramètre facet_grid, qui utilise aussi la syntaxe équation, permet de créer des facettes plus compliquées que celles créées par le paramètre facet_wrap, même si, dans nos exemples, on aurait pu utiliser aussi bien l’un que l’autre.

Le graphique ci-dessus présente un problème fréquent : l’axe horizontal du graphique, très important puisque Reinhart et Rogoff évoquent un seuil fatidique, pour la croissance, de 90% du PIB, est illisible. Grâce à l’argument scale_x_continuous, on va pouvoir clarifier cet axe en n’y faisant figurer que certaines valeurs :

p + geom_point() +
  facet_grid(. ~ Decade) +
  scale_x_continuous(breaks = seq(0, 200, by = 100))

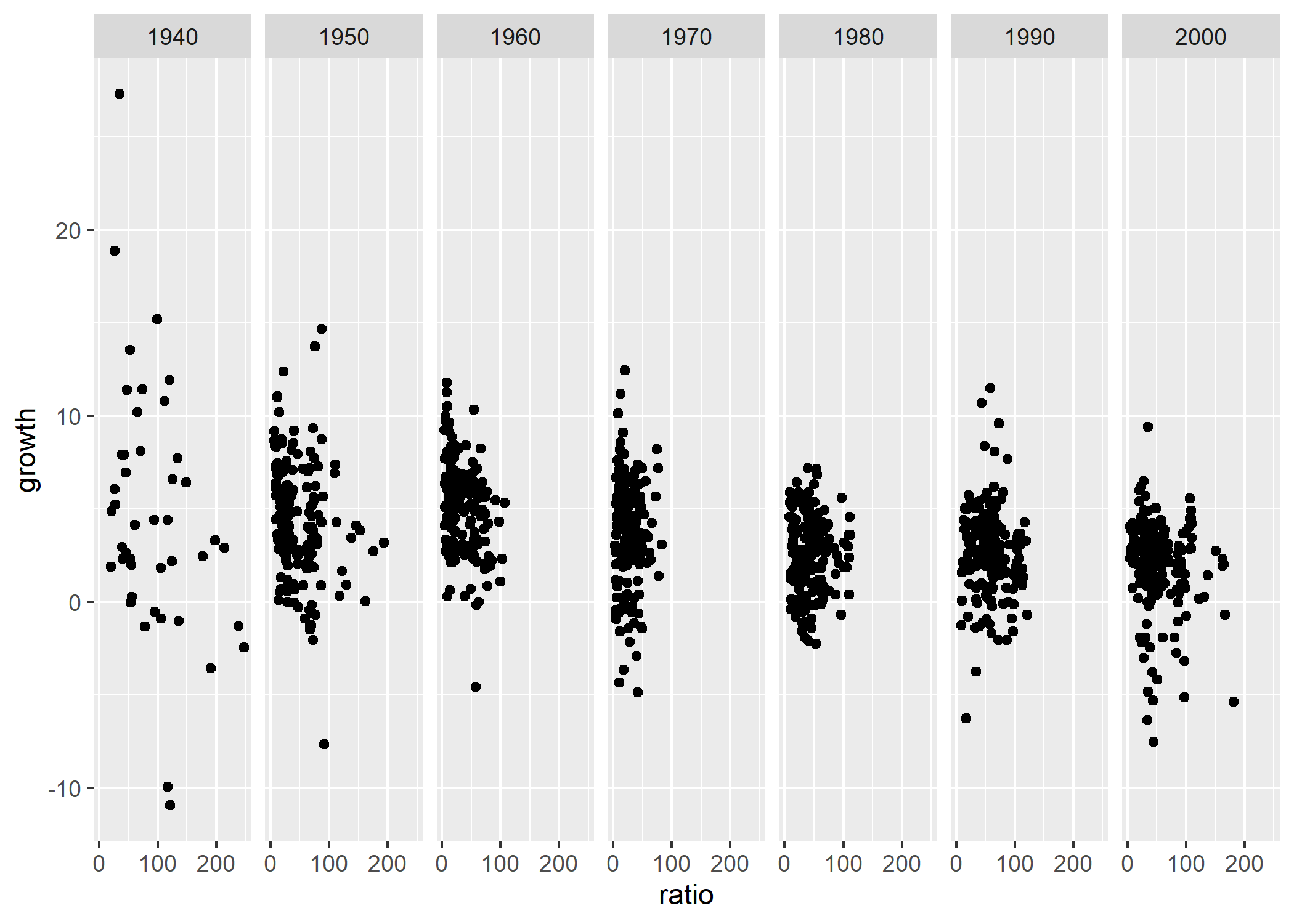
Ces réglages nous conviennent : on va donc les sauvegarder dans l’objet p, de manière à continuer de construire notre graphique en incluant ces différents éléments.

p <- p + geom_point() +
  facet_grid(. ~ Decade) +
  scale_x_continuous(breaks = seq(0, 200, by = 100))

Couleurs et échelles

Abordons désormais un élément-clé de ggplot2 : la manipulation des paramètres esthétiques. Précédemment, on n’a montré que deux de ces paramètres : x et y, les coordonnées du graphique. Mais ces paramètres peuvent aussi influencer la couleur des points de notre graphique comme le montre l’exemple suivant :

p + aes(color = ratio < 90)

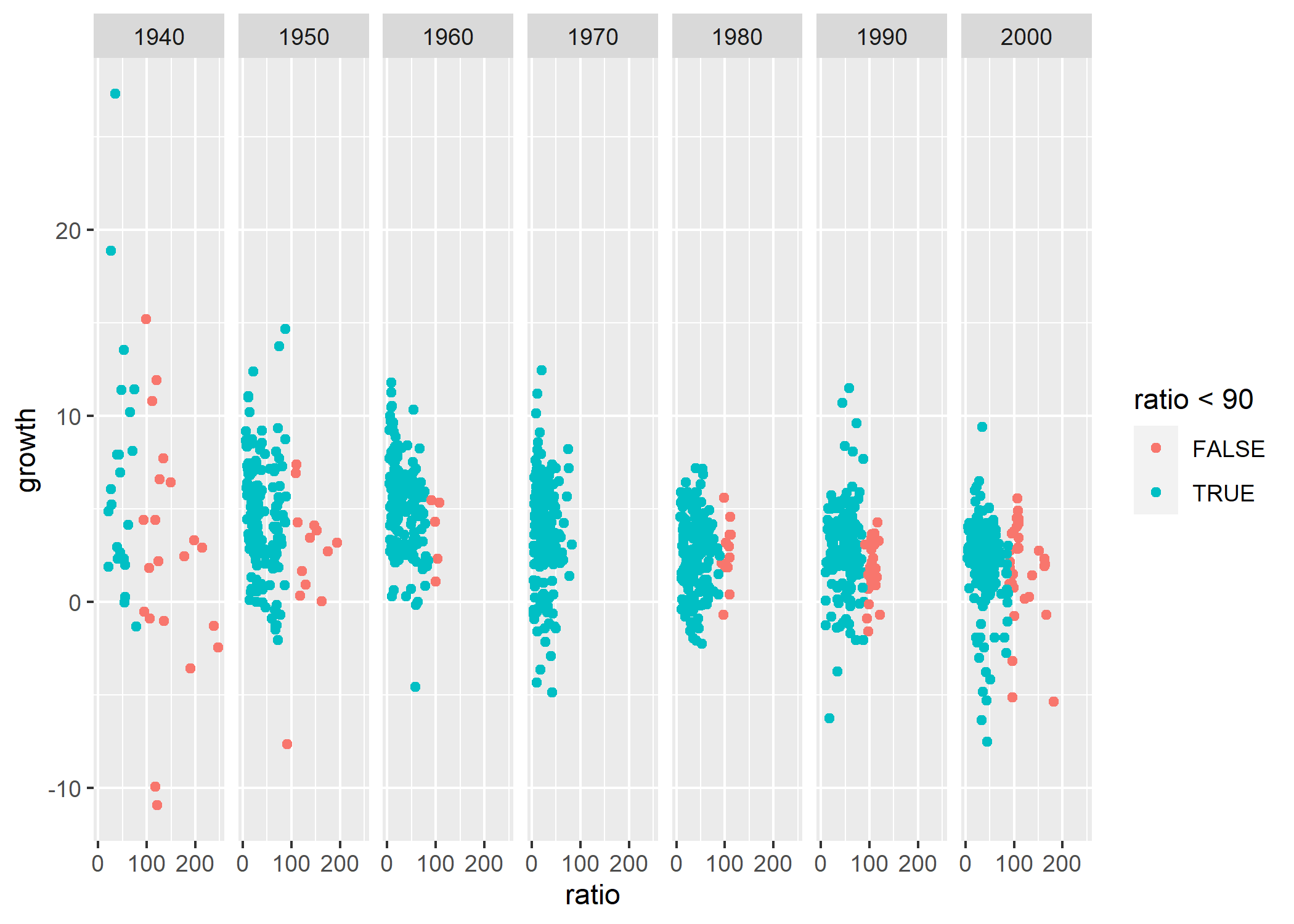
Qu’a-t-on fait ici ? On a rajouté, au graphique stocké dans p, un paramètre esthétique qui détermine la couleur de ses points en fonction d’une inégalité, ratio < 90, qui est vraie quand le ratio Dette publique / PIB est inférieur au seuil fatidique de Reinhart et Rogoff, et fausse quand ce ratio dépasse ce seuil. Les couleurs des points correspondent aux couleurs par défaut de ggplot2, que l’on peut très facilement modifier avec scale_colour_brewer :

p + aes(color = ratio < 90) +
  scale_colour_brewer(palette = "Set1")

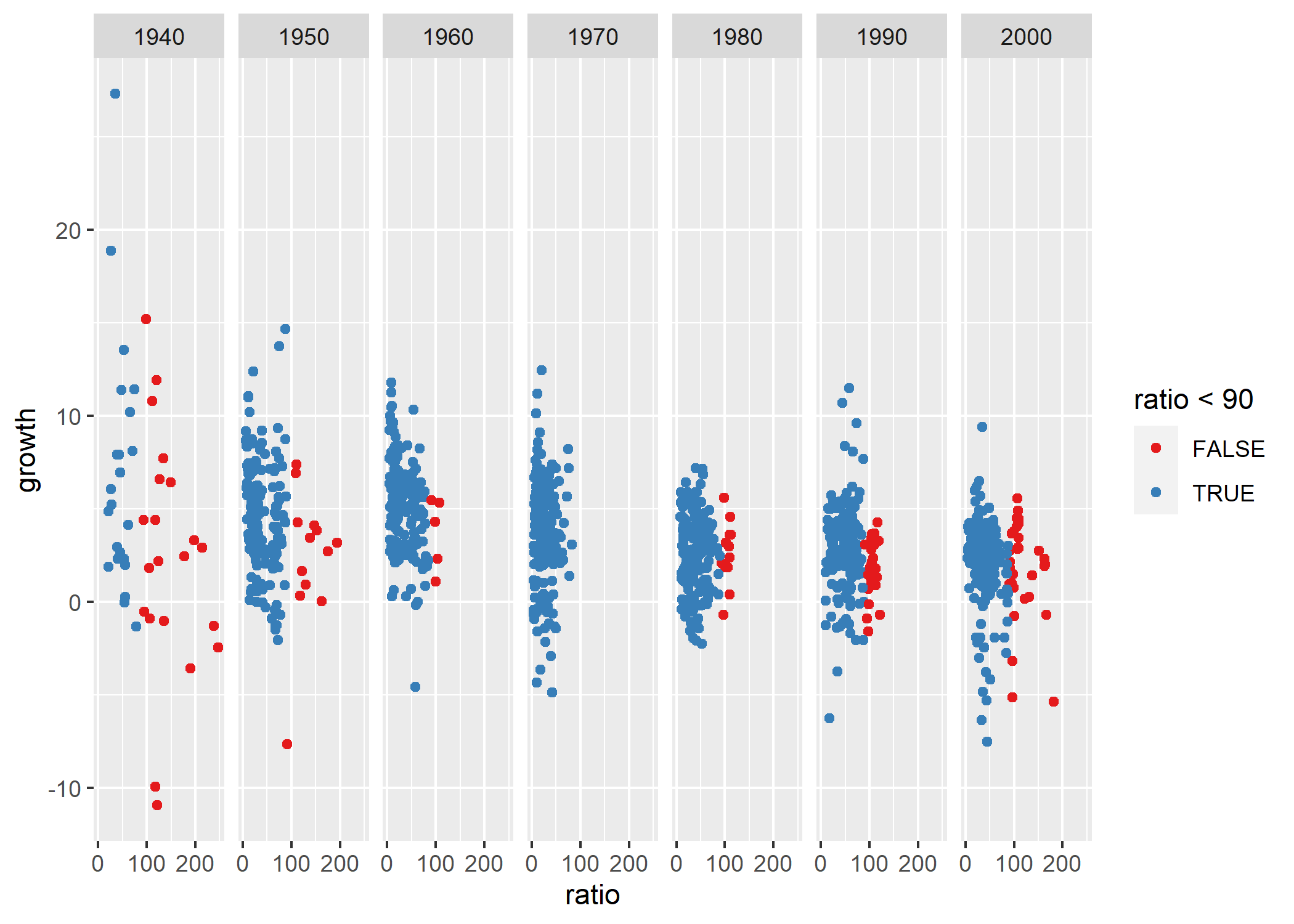
Ici, on a fait appel à la palette de couleur Set1 de l’éventail de couleurs ColorBrewer, qui est automatiquement disponible dans ggplot2, et qui est contenu dans l’extension RColorBrewer. La palette de couleurs que l’on a choisie affiche les points situés au-dessus du seuil fatidique de Reinhart et Rogoff en rouge, les autres en bleu.

Que peut-on dire, à ce stade, du seuil fatidique de Reinhart et Rogoff ? On peut observer qu’après la Seconde guerre mondiale, de nombreux pays sont déjà endettés au-delà de ce seuil, et dégagent déjà moins de croissance que les autres. Sur la base de cette trajectoire, de nombreux critiques de Reinhart et Rogoff ont fait remarquer que le raisonnement de Reinhart et Rogoff pose en réalité un sérieux problème d’inversion du rapport causal entre endettement et croissance au cours du temps.

Envisageons une nouvelle modification des paramètres graphiques. La légende du graphique, qui affiche FALSE et TRUE en fonction de l’inégalité ratio < 90, peut être déroutante. Clarifions un peu cette légende en supprimant son titre et en remplaçant les libellés (labels) FALSE et TRUE par leur signification :

p <- p + aes(color = ratio < 90) +
  scale_color_brewer("", palette = "Set1",
                     labels = c("ratio > 90", "ratio < 90"))

Dans le bloc de code ci-dessus, on a stocké l’ensemble de nos modifications dans l’objet p, sans l’afficher ; en effet, on souhaite encore procéder à une dernière modification, en rajoutant une régression locale à travers les points de chaque facette5. Après consultation de la documentation de ggplot2 ici et là, on en arrive au code ci-dessous, où p produit le graphique précédent et geom_smooth produit la régression locale :

p + geom_smooth(method = "loess", se = FALSE,
                size = 1, color = "black")
`geom_smooth()` using formula = 'y ~ x'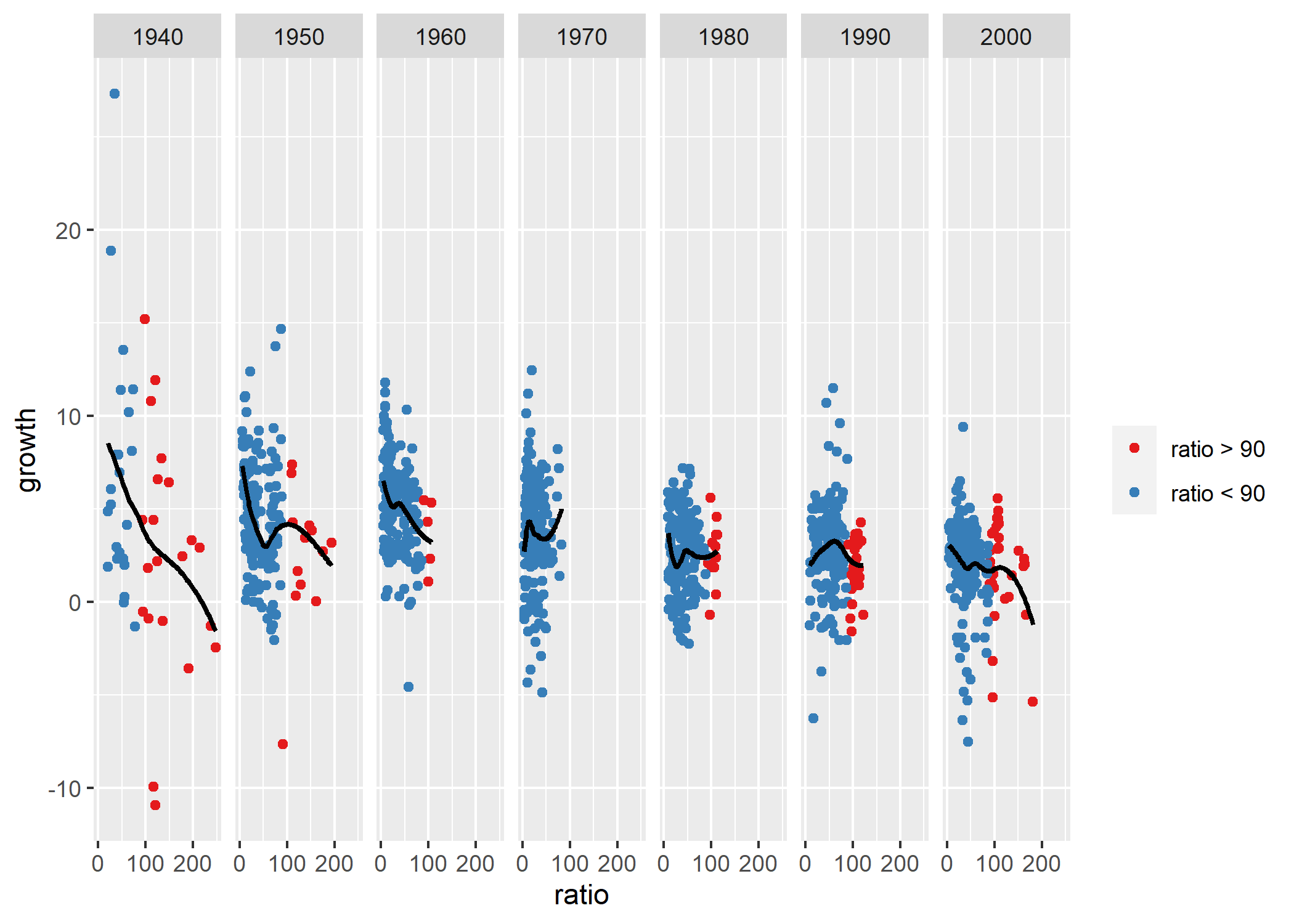

Le graphique permet d’évaluer de manière encore un peu plus précise l’argument de Reinhart et Rogoff, et en particulier la nature pas si fatidique du seuil de 90% du ratio “Dette publique / PIB”, qui sans être une bonne nouvelle pour l’économie, ne détermine pas fatidiquement la direction du taux de croissance : si c’était le cas, toutes les courbes du graphique ressembleraient à celles des années 2000. Autrement dit, l’argumentaire de Reinhart et Rogoff laisse clairement à désirer.

Utilisation des thèmes

Reprenons notre graphique de départ. On va, pour terminer cette démonstration, en construire une version imprimable en noir et blanc, ce qui signifie qu’au lieu d’utiliser des couleurs pour distinguer les points en-deçà et au-delà du seuil fatidique de Reinhart et Rogoff, on va utiliser une ligne verticale, produite par geom_vline et affichée en pointillés par le paramètre lty (linetype) :

ggplot(data = debt, aes(y = growth, x = ratio)) + 
  geom_point(color = "grey50") +
  geom_vline(xintercept = 90, lty = "dotted") +
  geom_smooth(method = "loess", size = 1, color = "black", se = FALSE) +
  scale_x_continuous(breaks = seq(0, 200, by = 100)) +
  facet_grid(. ~ Decade) +
  labs(y = "Taux de croissance du produit intérieur brut\n",
       x = "\nRatio dette publique / produit intérieur brut (%)",
       title = "Données Reinhart et Rogoff corrigées, 1946-2009\n") +
  theme_bw() +
  theme(strip.background = element_rect(fill = "grey90", color = "grey50"),
        strip.text = element_text(size = rel(1)),
        panel.grid = element_blank())
`geom_smooth()` using formula = 'y ~ x'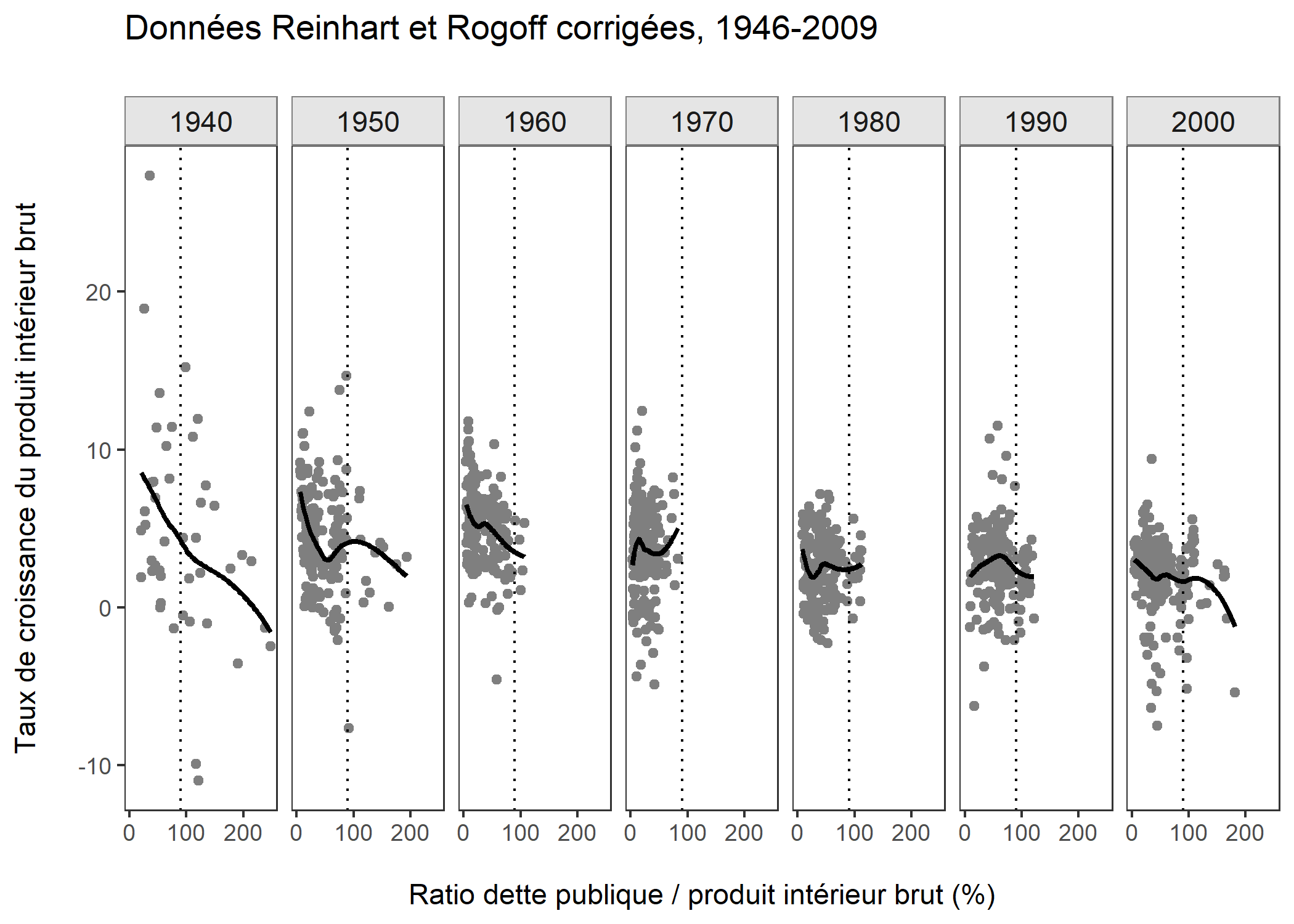

Ce graphique utilise tous les éléments présentés dans ce chapitre, ainsi qu’une dernière nouveauté : l’utilisation d’un thème graphique différent du thème par défaut de ggplot2. Le thème par défaut, qui s’appelle theme_grey, est ici remplacé par un thème moins chargé, theme_bw (“black and white”), que l’on a modifié en y rajoutant quelques paramètres supplémentaires :

  • le paramètre strip.background détermine la couleur du rectangle contenant les titres des facettes, c’est-à-dire les décennies observées ;
  • le paramètre strip.text détermine la taille des titres des facettes, qui sont ici affichés dans la même taille de texte que le reste du texte ;
  • et le paramètre panel.grid supprime ici les guides du graphique grâce à l’élément vide element_blank, de manière à en alléger la lecture.

Ces différents réglages peuvent être sauvegardés de manière à créer des thèmes réutilisables, comme ceux de l’extension ggthemes, ce qui permet par exemple de créer un thème entièrement blanc dans lequel on peut ensuite projeter une carte, ou de produire une série de graphiques homogènes d’un point de vue esthétique.

Export des graphiques

Les graphiques produits par ggplot2 peuvent être sauvegardés manuellement, comme expliqué dans le chapitre Export des graphiques, ou programmatiquement. Pour sauvegarder le dernier graphique affiché par ggplot2 au format PNG, il suffit d’utiliser la fonction ggsave, qui permet d’en régler la taille (en pouces) et la résolution (en pixels par pouce ; 72 par défaut) :

ggsave("reinhart-rogoff.png", width = 11, height = 8)

De la même manière, pour sauvegarder n’importe quel graphique construit avec ggplot2 et stocké dans un objet, il suffit de préciser le nom de cet objet, comme ci-dessous, où l’on sauvegarde le graphique contenu dans l’objet p au format vectoriel PDF, qui préserve la netteté du texte et des autres éléments du graphique à n’importe quelle résolution d’affichage :

ggsave("reinhart-rogoff.pdf", plot = p,
       width = 11, height = 8)

Pour aller plus loin

Ce chapitre n’a pu faire la démonstration que d’une infime partie des manières d’utiliser ggplot2. En voici une dernière illustration, qui donne une idée des différents types de graphiques que l’extension permet de produire dès que l’on connaît les principaux éléments de sa syntaxe :

ggplot(data = debt, aes(x = ratio > 90, y = growth)) +
  geom_boxplot() +
  scale_x_discrete(labels = c("< 90", "90+")) +
  facet_grid(. ~ Decade) +
  labs(y = "Taux de croissance du produit intérieur brut\n",
       x = "\nRatio dette publique / produit intérieur brut (%)",
       title = "Données Reinhart et Rogoff corrigées, 1946-2009\n") +
  theme_linedraw() +
  theme(strip.text = element_text(size = rel(1)),
        panel.grid = element_blank())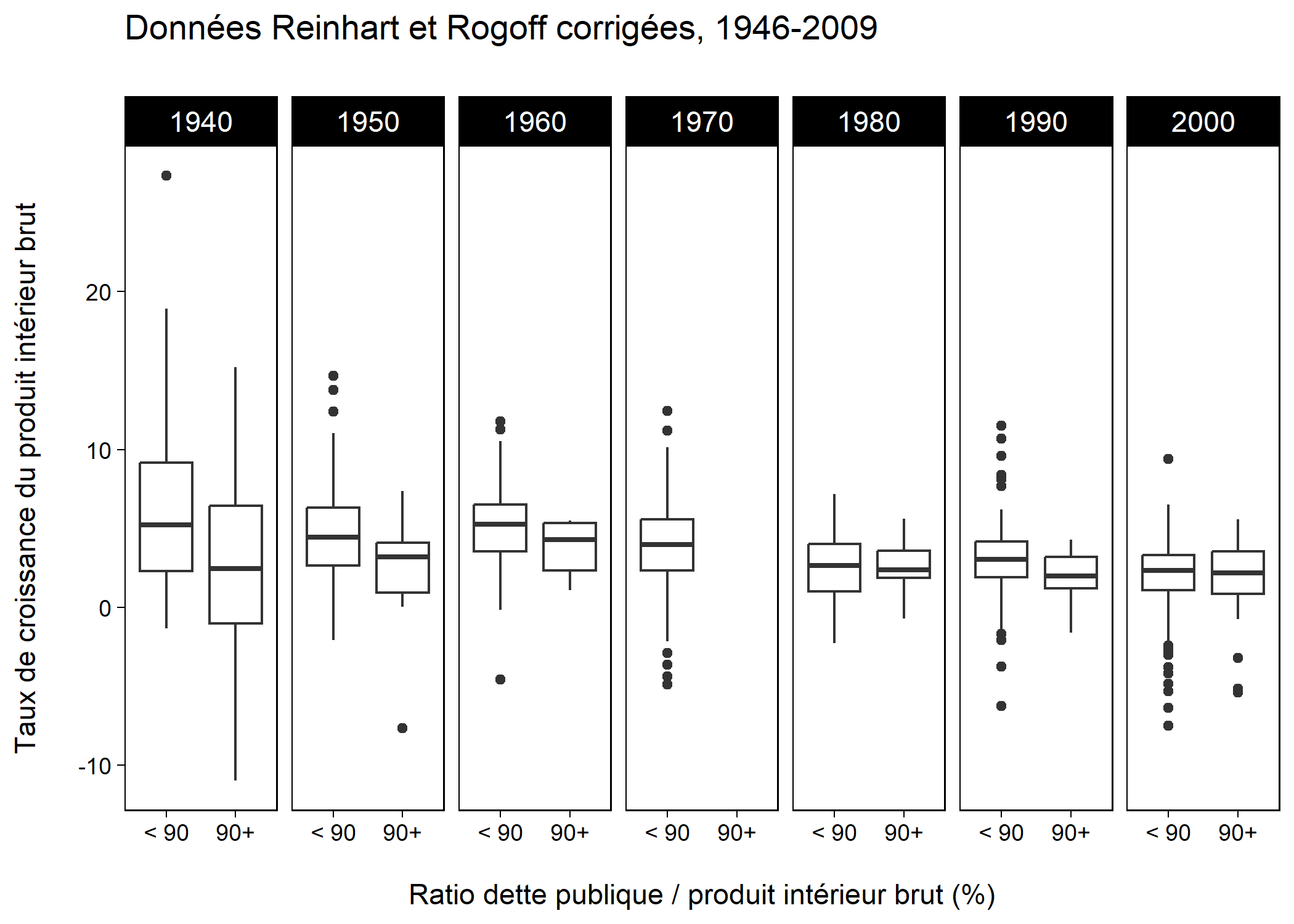

Le code ci-dessus est somme toute très proche du code présenté dans le reste du texte, et en même temps, on a basculé de la visualisation sous forme de série temporelles à une visualisation par boxplots. Ces basculements sont très faciles à envisager dès que l’on maîtrise les principaux éléments de ggplot2, geom, scale et facet, et les paramètres labs et theme pour effectuer les finitions.

Ressources essentielles

Pour tout ce qui concerne l’utilisation de ggplot2, l’ouvrage de Wickham, en cours d’actualisation, est la ressource essentielle à consulter. L’ouvrage de Winston Chang, qui contient des dizaines d’exemples, le complète utilement, de même que la documentation en ligne de l’extension. Enfin, le site StackOverflow contient de très nombreuses questions/réponses sur les subtilités de sa syntaxe.

On trouve aussi très facilement, ailleurs sur Internet, des dizaines de tutorials et autres cheatsheets pour ggplot2, ici ou là par exemple.

A noter également une gallerie de graphiques sous R avec de très nombreux exemples de graphique ggplot2 : http://www.r-graph-gallery.com/portfolio/ggplot2-package/

Extensions de ggplot2

Il faut signaler, pour terminer, quelques-unes des différentes extensions inspirées de ggplot2, dont la plupart sont encore en cours de développement, mais qui permettent d’ores et déjà de produire des centaines de types de graphiques différents, à partir d’une syntaxe graphique proche de celle présentée dans ce chapitre :

  1. Voir l’excellente documentation de l’extension et les autres ressources citées en fin de chapitre.↩︎

  2. Bien que l’on ait fait le choix de présenter l’extension ggplot2 plutôt que l’extension lattice, celle-ci reste un excellent choix pour la visualisation, notamment, de panels et de séries temporelles. On trouve de très beaux exemples d’utilisation de lattice en ligne, mais un peu moins de documentation, et beaucoup moins d’extensions, que pour ggplot2.↩︎

  3. Ce produit est mesuré en termes réels, de manière à ce que le calcul de sa croissance ne soit pas affecté par l’inflation.↩︎

  4. Plus précisément, cela introduit un retour à la ligne dans le titre de l’axe.↩︎

  5. La régression locale est une variante du calcul de la moyenne glissante (ou moyenne mobile) d’une courbe.↩︎