Comparaisons (moyennes et proportions)
Une version actualisée de ce chapitre est disponible sur guide-R : Statistique bivariée & Tests de comparaison
Ce chapitre est évoqué dans le webin-R #03 (statistiques descriptives avec gtsummary et esquisse) sur YouTube.
Nous utiliserons dans ce chapitre les données de l’enquête Histoire de vie 2003 fournies avec l’extension questionr.
Comparaison de moyennes
On peut calculer la moyenne d’âge des deux groupes en utilisant la fonction tapply1 :
Non Oui
48.30211 27.57143 L’écart est important. Est-il statistiquement significatif ? Pour cela on peut faire un test t de Student de comparaison de moyennes à l’aide de la fonction t.test :
Welch Two Sample t-test
data: age by hard.rock
t = 9.6404, df = 13.848, p-value = 1.611e-07
alternative hypothesis: true difference in means between group Non and group Oui is not equal to 0
95 percent confidence interval:
16.11379 25.34758
sample estimates:
mean in group Non mean in group Oui
48.30211 27.57143 Le test est extrêmement significatif. L’intervalle de confiance à 95 % de la différence entre les deux moyennes va de 16,1 ans à 25,3 ans.
La valeur affichée pour p est de 1.611e-07. Cette valeur peut paraître étrange pour les non avertis. Cela signifie tout simplement 1,611 multiplié par 10 à la puissance -7, autrement dit 0,0000001611. Cette manière de représenter un nombre est couramment appelée notation scientifique.
Pour plus de détails, voir http://fr.wikipedia.org/wiki/Notation_scientifique.
Il est possible de désactiver la notation scientifique avec la commande :
Pour rétablir la notation scientifique :
Nous sommes cependant allés un peu vite en besogne, car nous avons négligé une hypothèse fondamentale du test t : les ensembles de valeur comparés doivent suivre approximativement une loi normale et être de même variance2.
Dans le test de Student, on suppose l’égalité des variances parentes, ce qui permet de former une estimation commune de la variance des deux échantillons (on parle de pooled variance), qui revient à une moyenne pondérée des variances estimées à partir des deux échantillons. Dans le cas où l’on souhaite relaxer cette hypothèse, le test de Welch ou la correction de Satterthwaite reposent sur l’idée que l’on utilise les deux estimations de variance séparément, suivie d’une approximation des degrés de liberté pour la somme de ces deux variances. Le même principe s’applique dans le cas de l’analyse de variance à un facteur (cf. oneway.test).
Comment vérifier que l’hypothèse de normalité est acceptable pour ces données ? D’abord avec un petit graphique composés de deux histogrammes :
par(mfrow = c(1, 2))
hist(d$age[d$hard.rock == "Oui"], main = "Hard rock", col = "red")
hist(d$age[d$hard.rock == "Non"], main = "Sans hard rock", col = "red")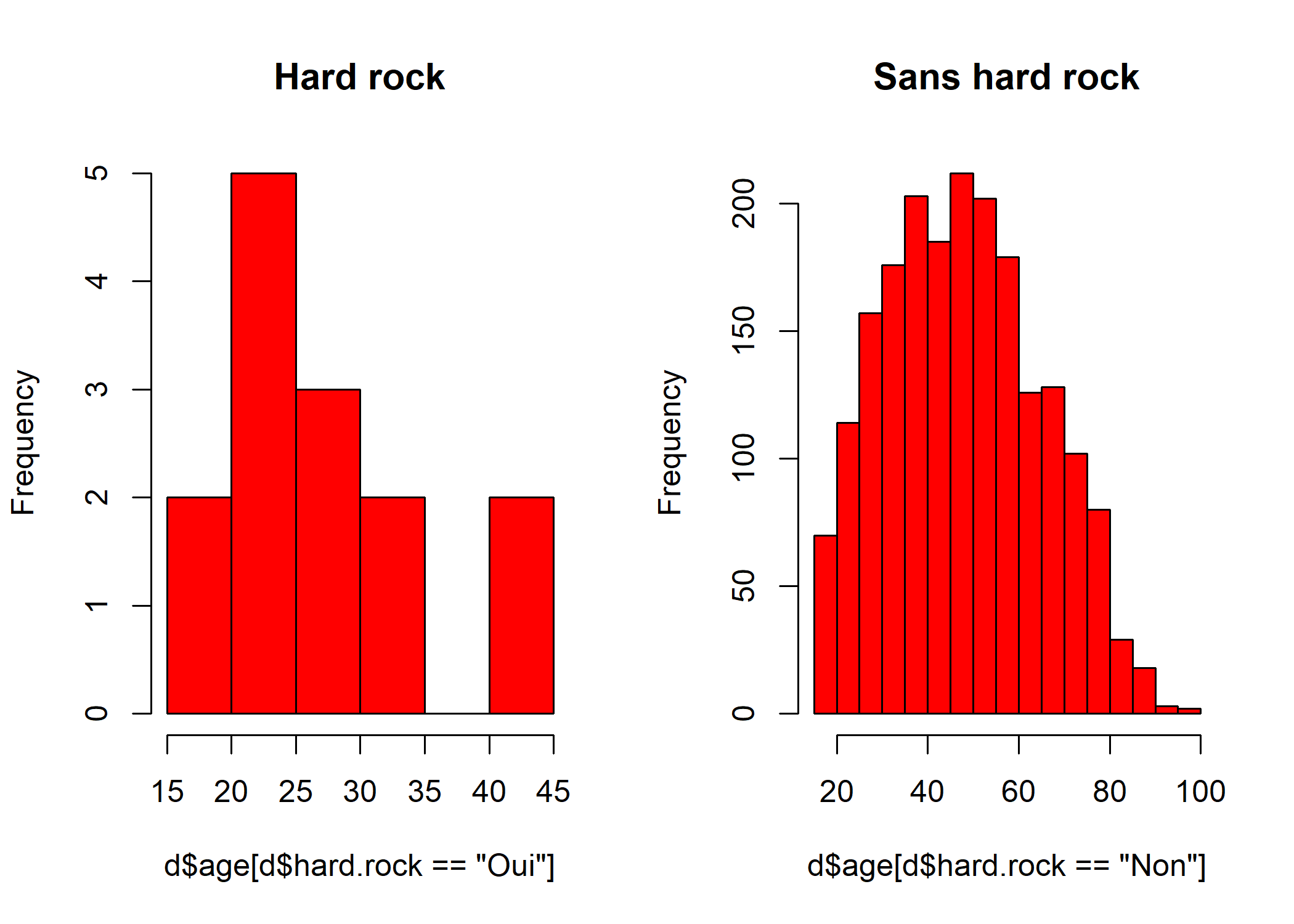
Une alternative consisterait à utiliser des graphiques de type QQ-plot, à l’aide de la fonction qnorm, même si leur utilisation et leur interprétation ne sera pas détaillée ici.
La fonction par permet de modifier de nombreux paramètres graphiques. Ici, l’instruction par(mfrow = c(1, 2)) sert à indiquer que l’on souhaite afficher deux graphiques sur une même fenêtre, plus précisément que la fenêtre doit comporter une ligne et deux colonnes.
Ça a l’air à peu près bon pour les « Sans hard rock », mais un peu plus limite pour les fans de Metallica, dont les effectifs sont d’ailleurs assez faibles. Si on veut en avoir le cœur net on peut utiliser le test de normalité de Shapiro-Wilk avec la fonction shapiro.test :
Shapiro-Wilk normality test
data: d$age[d$hard.rock == "Oui"]
W = 0.86931, p-value = 0.04104
Shapiro-Wilk normality test
data: d$age[d$hard.rock == "Non"]
W = 0.98141, p-value = 2.079e-15Visiblement, le test estime que les distributions ne sont pas suffisamment proches de la normalité dans les deux cas.
Et concernant l’égalité des variances ?
Non Oui
285.62858 62.72527 L’écart n’a pas l’air négligeable. On peut le vérifier avec le test d’égalité des variances fourni par la fonction var.test :
F test to compare two variances
data: age by hard.rock
F = 4.5536, num df = 1985, denom df = 13, p-value =
0.003217
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
1.751826 8.694405
sample estimates:
ratio of variances
4.553644 La différence est très significative. En toute rigueur le test t n’aurait donc pas pu être utilisé. Cela dit, il convient de rappeler que ce test statistique (1) suppose la normalité des distributions et (2) considère comme hypothèse nulle l’égalité des variances (parentes) – ce que l’on souhaiterait vérifier alors qu’on ne peut pas accepter l’hypothèse nulle dans un cadre d’inférence fréquentiste – sans que l’on définisse réellement ce que signifie des variances différentes sur le plan pratique. Est-ce qu’une variation de la variance du simple au double est pertinente au regard du domaine d’étude, ou bien faut-il décider qu’à partir d’un rapport de 4 on peut considérer qu’il y a bien une différence importante entre deux variances ? Sans avoir fixé au préalable cette hypothèse alternative, on ne peut guère conclure à partir de ce test. Une alternative consiste à comparer la forme des distributions à l’aide, par exemple, de diagrammes de type boîtes à moustaches.
Comparaison des rangs ou de la médiane
Damned ! Ces maudits tests statistiques vont-ils nous empêcher de faire connaître au monde entier notre fabuleuse découverte sur l’âge des fans de Sepultura ? Non ! Car voici qu’approche à l’horizon un nouveau test, connu sous le nom de Wilcoxon/Mann-Whitney. Celui-ci a l’avantage d’être non-paramétrique, c’est à dire de ne faire aucune hypothèse sur la distribution des échantillons comparés, à l’exception que celles-ci ont des formes à peu près comparables (essentiellement en termes de variance). Attention, il ne s’agit pas d’un test comparant les différences de médianes (pour cela il existe le test de Mood) mais d’un test reposant sur la somme des rangs des observations, au lieu des valeurs
brutes, dans les deux groupes, via la fonction wilcox.test :
Wilcoxon rank sum test with continuity correction
data: age by hard.rock
W = 23980, p-value = 2.856e-06
alternative hypothesis: true location shift is not equal to 0Ouf ! La différence est hautement significative3. Nous allons donc pouvoir entamer la rédaction de notre article pour la Revue française de sociologie.
Note : le test de Wilcoxon n’est pas adapté pour comparer les rangs lorsque l’on a trois groupes ou plus. On pourra dans ce cas là avoir recours au test de Kruskal-Wallis avec la fonction krukal.test.
Kruskal-Wallis rank sum test
data: age by hard.rock
Kruskal-Wallis chi-squared = 21.913, df = 1, p-value
= 2.852e-06Note 2 : le test de Mood mentionné plus haut peut être réalisé avec mood.test.
Mood two-sample test of scale
data: age by hard.rock
Z = -3.1425, p-value = 0.001675
alternative hypothesis: two.sidedComparaison de proportions
La fonction prop.test, que nous avons déjà rencontrée pour calculer l’intervalle de confiance d’une proportion (voir le chapitre dédié aux intervalles de confiance) permets également d’effectuer un test de comparaison de deux proportions.
Supposons que l’on souhaite comparer la proportion de personnes faisant du sport entre ceux qui lisent des bandes dessinées et les autres :
sport
lecture.bd Non Oui Total
Non 64.2 35.8 100.0
Oui 48.9 51.1 100.0
Ensemble 63.8 36.1 100.0Une représentation graphique sous forme de diagramme en barres peut être définie comme suit :
barplot(prop.table(tab, margin = 1) * 100, beside = TRUE, ylim = c(0, 100), xlab = "Sport", legend.text = c("Lecture : non", "Lecture : oui"))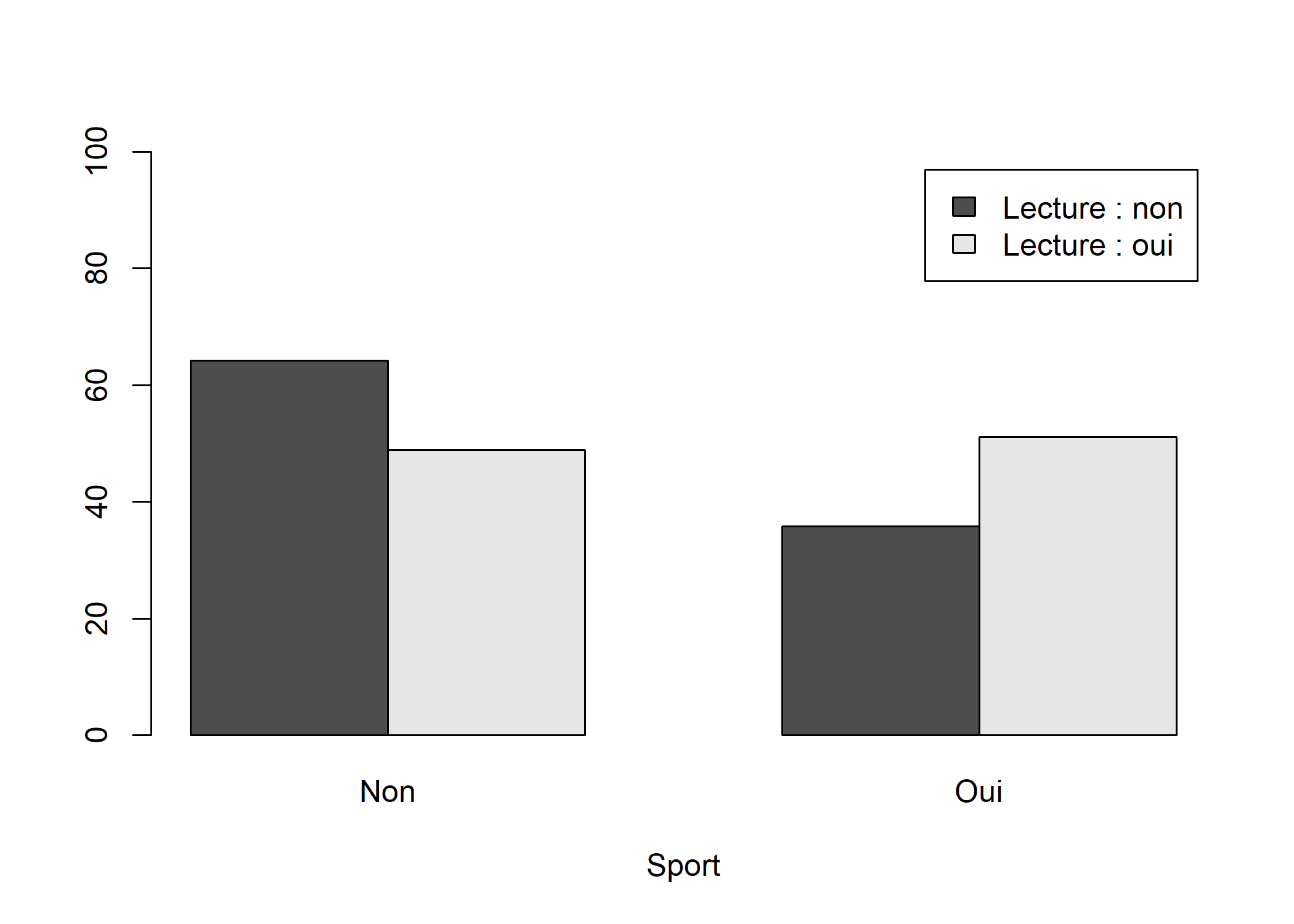
Il suffit de transmettre notre tableau croisé (à 2×2 dimensions) à prop.test :
2-sample test for equality of proportions with
continuity correction
data: tab
X-squared = 4, df = 1, p-value = 0.0455
alternative hypothesis: two.sided
95 percent confidence interval:
-0.002652453 0.308107236
sample estimates:
prop 1 prop 2
0.6420891 0.4893617 On pourra également avoir recours à la fonction fisher.test qui renverra notamment l’odds ratio et son intervalle de confiance correspondant :
Fisher's Exact Test for Count Data
data: tab
p-value = 0.0445
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
1.003372 3.497759
sample estimates:
odds ratio
1.871433 Formellement, le test de Fisher suppose que les marges du tableau (totaux lignes et colonnes) sont fixées, puisqu’il repose sur une loi hypergéométrique, et donc celui-ci se prête plus au cas des situations expérimentales (plans d’expérience, essais cliniques) qu’au cas des données tirées d’études observationnelles.
On pourra aussi avoir recours à la fonction odds.ratio de l’extension questionr qui réalise le même calcul mais présente le résultat légèrement différemment :
Note : pour le calcul du risque relatif, on pourra regarder du côté de la fonction relrisk de l’extension mosaic.
χ² et dérivés
Dans le cadre d’un tableau croisé, on peut tester l’existence d’un lien entre les modalités de deux variables, avec le très classique test du χ² de Pearson4. Celui-ci s’obtient grâce à la fonction chisq.test, appliquée au tableau croisé obtenu avec table ou xtabs5 :
d$qualreg <- as.character(d$qualif)
d$qualreg[d$qualif %in% c("Ouvrier specialise", "Ouvrier qualifie")] <- "Ouvrier"
d$qualreg[d$qualif %in% c(
"Profession intermediaire",
"Technicien"
)] <- "Intermediaire"
tab <- table(d$sport, d$qualreg)
tab
Autre Cadre Employe Intermediaire Ouvrier
Non 38 117 401 127 381
Oui 20 143 193 119 114
Pearson's Chi-squared test
data: tab
X-squared = 96.798, df = 4, p-value < 2.2e-16Le test est hautement significatif : on ne peut donc pas considérer qu’il y a indépendance entre les lignes et les colonnes du tableau.
Notons que l’agrégation des niveaux d’une variable catégorielle peut être réalisée d’une manière différente en utilisant les fonctions de gestion des niveaux d’un facteur. Les expressions précédentes sont donc équivalentes à l’approche ci-après, qui ne nécessite pas de convertir d$qualif en chaîne de caractères :
On peut affiner l’interprétation du test en déterminant dans quelle cas l’écart à l’indépendance est le plus significatif en utilisant les résidus du test. Ceux-ci sont notamment affichables avec la fonction chisq.residuals de questionr :
Autre Cadre Employe Intermediaire Ouvrier
Non 0.11 -3.89 0.95 -2.49 3.49
Oui -0.15 5.23 -1.28 3.35 -4.70Les cases pour lesquelles l’écart à l’indépendance est significatif ont un résidu dont la valeur est supérieure à 2 ou inférieure à -2 (le fameux nombre 2 issu de la loi normale, au-delà duquel on s’attend à observer au maximum 2,5 % des observations). Ici on constate que la pratique d’un sport est sur-représentée parmi les cadres et, à un niveau un peu moindre, parmi les professions intermédiaires, tandis qu’elle est sous-représentée chez les ouvriers.
Enfin, on peut calculer le coefficient de contingence de Cramer du tableau, qui présente l’avantage de pouvoir être comparé par la suite à celui calculé sur d’autres tableaux croisés. On peut pour cela utiliser la fonction cramer.v de questionr :
[1] 0.24199Pour un tableau à 2×2 entrées, comme discuté plus haut, il est également possible de calculer le test exact de Fisher avec la fonction fisher.test. On peut soit lui passer le résultat de table ou xtabs, soit directement les deux variables à croiser.
Non Oui Total
Homme 70.0 30.0 100.0
Femme 44.5 55.5 100.0
Ensemble 56.0 44.0 100.0
Fisher's Exact Test for Count Data
data: table(d$sexe, d$cuisine)
p-value < 2.2e-16
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
2.402598 3.513723
sample estimates:
odds ratio
2.903253 Le test du χ² de Pearson étant assez robuste quant aux déviations par rapport aux hypothèses d’applications du test (effectifs théoriques tous ≥ 5), le test de Fisher présente en général peu d’intérêt dans le cas de l’analyse des tableaux de contingence.
Données pondérées et l’extension survey
Lorsque l’on utilise des données pondérées, on aura recours à l’extension survey6.
Préparons des données d’exemple :
Pour comparer deux moyennes à l’aide d’un test t on aura recours à svyttest :
Design-based t-test
data: age ~ sexe
t = 2.0404, df = 1998, p-value = 0.04144
alternative hypothesis: true difference in mean is not equal to 0
95 percent confidence interval:
0.08316148 4.19909687
sample estimates:
difference in mean
2.141129 Pour le test de Wilcoxon/Mann-Whitney, on pourra avoir recours à svyranktest :
Design-based KruskalWallis test
data: age ~ hard.rock
t = -11.12, df = 1998, p-value < 2.2e-16
alternative hypothesis: true difference in mean rank score is not equal to 0
sample estimates:
difference in mean rank score
-0.3636859 On ne peut pas utiliser chisq.test directement sur un tableau généré par svytable. Les effectifs étant extrapolés à partir de la pondération, les résultats du test seraient complètement faussés. Si on veut faire un test du χ² sur un tableau croisé pondéré, il faut utiliser svychisq :
clso
sexe Oui Non Ne sait pas Total
Homme 51.6 47.0 1.4 100.0
Femme 43.9 54.8 1.3 100.0
Ensemble 47.5 51.1 1.4 100.0
Pearson's X^2: Rao & Scott adjustment
data: svychisq(~sexe + clso, dw)
F = 3.3331, ndf = 1.9734, ddf = 3944.9024, p-value =
0.03641L’extension survey ne propose pas de version adaptée du test exact de Fisher. Pour comparer deux proportions, on aura donc recours au test du χ² :
sport
lecture.bd Non Oui Total
Non 61.0 39.0 100.0
Oui 46.8 53.2 100.0
Ensemble 60.7 39.3 100.0
Pearson's X^2: Rao & Scott adjustment
data: svychisq(~lecture.bd + sport, dw)
F = 2.6213, ndf = 1, ddf = 1999, p-value = 0.1056Tests dans les tableaux de gtsummary
Lorsque l’on réalise un tableau croisé avec tbl_summary ou tbl_svysummary de l’extension gtsummary, il est possible d’ajouter des tests de comparaison avec add_p.
Setting theme `language: fr`| Caractéristique | Non, N = 1 9861 | Oui, N = 141 | p-valeur2 |
|---|---|---|---|
| age | 48 (35 – 60) | 26 (22 – 30) | <0,001 |
| sport | >0,9 | ||
| Non | 1 268 (64%) | 9 (64%) | |
| Oui | 718 (36%) | 5 (36%) | |
| 1 Médiane (EI); n (%) | |||
| 2 test de Wilcoxon-Mann-Whitney; test du khi-deux d'indépendance | |||
Il est possible de préciser le type de test à utiliser.
d %>%
tbl_summary(
include = c("hard.rock", "age"),
by = "hard.rock"
) %>%
add_p(test = list(all_continuous() ~ "wilcox.test"))| Caractéristique | Non, N = 1 9861 | Oui, N = 141 | p-valeur2 |
|---|---|---|---|
| age | 48 (35 – 60) | 26 (22 – 30) | <0,001 |
| 1 Médiane (EI) | |||
| 2 test de Wilcoxon-Mann-Whitney | |||
Cela fonctionne également avec les données pondérées et les plans d’échantillonnage complexe.
| Caractéristique | Non, N = 10 981 9631 | Oui, N = 89 2641 | p-valeur2 |
|---|---|---|---|
| age | 45 (31 – 60) | 23 (19 – 28) | <0,001 |
| sport | 0,8 | ||
| Non | 6 656 841 (61%) | 57 920 (65%) | |
| Oui | 4 325 122 (39%) | 31 344 (35%) | |
| 1 Médiane (EI); n (%) | |||
| 2 test de Wilcoxon sur la somme des rangs adapté aux plans d'échantillonnage complexes; test du Chi² avec la correction du second ordre de Rao & Scott | |||
La fonction
tapplyest présentée plus en détails dans le chapitre Manipulation de données.↩︎Concernant cette seconde condition,
t.testutilise par défaut un test de Welch qui ne suppose pas l’égalité des variances parentes ; il est toutefois possible d’utiliser le test classique de Student en spécifiant l’optionvar.equal = TRUE.↩︎Ce test peut également fournir un intervalle de confiance avec l’option
conf.int=TRUE.↩︎On ne donnera pas plus d’indications sur le test du χ² ici. Les personnes désirant une présentation plus détaillée pourront se reporter (attention, séance d’autopromotion !) à la page suivante : http://alea.fr.eu.org/pages/khi2.↩︎
On peut aussi appliquer directement le test en spécifiant les deux variables à croiser via
chisq.test(d$qualreg, d$sport).↩︎Voir le chapitre dédié aux données pondérées.↩︎

