Marginal Predictions with marginaleffects::avg_predictions()

Use marginaleffects::avg_predictions() to estimate marginal predictions for each variable of a model and return a tibble tidied in a way that it could be used by broom.helpers functions. See marginaleffects::avg_predictions() for a list of supported models.

Usage

tidy_marginal_predictions(
  x,
  variables_list = "auto",
  conf.int = TRUE,
  conf.level = 0.95,
  ...
)

variables_to_predict(
  model,
  interactions = TRUE,
  categorical = unique,
  continuous = stats::fivenum
)

plot_marginal_predictions(x, variables_list = "auto", conf.level = 0.95, ...)

Arguments

x

(a model object, e.g. glm)
A model to be tidied.

variables_list

(list or string)
A list whose elements will be sequentially passed to variables in marginaleffects::avg_predictions() (see details below); alternatively, it could also be the string "auto" (default) or "no_interaction".

conf.int

(logical)
Whether or not to include a confidence interval in the tidied output.

conf.level

(numeric)
The confidence level to use for the confidence interval (between 0 ans 1).

...

Additional parameters passed to marginaleffects::avg_predictions().

model

(a model object, e.g. glm)
A model.

interactions

(logical)
Should combinations of variables corresponding to interactions be returned?

categorical

(predictor values)
Default values for categorical variables.

continuous

(predictor values)
Default values for continuous variables.

Details

Marginal predictions are obtained by calling, for each variable, marginaleffects::avg_predictions() with the same variable being used for the variables and the by argument.

Considering a categorical variable named cat, tidy_marginal_predictions() will call avg_predictions(model, variables = list(cat = unique), by = "cat") to obtain average marginal predictions for this variable.

Considering a continuous variable named cont, tidy_marginal_predictions() will call avg_predictions(model, variables = list(cont = "fivenum"), by = "cont") to obtain average marginal predictions for this variable at the minimum, the first quartile, the median, the third quartile and the maximum of the observed values of cont.

By default, average marginal predictions are computed: predictions are made using a counterfactual grid for each value of the variable of interest, before averaging the results. Marginal predictions at the mean could be obtained by indicating newdata = "mean". Other assumptions are possible, see the help file of marginaleffects::avg_predictions().

tidy_marginal_predictions() will compute marginal predictions for each variable or combination of variables, before stacking the results in a unique tibble. This is why tidy_marginal_predictions() has a variables_list argument consisting of a list of specifications that will be passed sequentially to the variables argument of marginaleffects::avg_predictions().

The helper function variables_to_predict() could be used to automatically generate a suitable list to be used with variables_list. By default, all unique values are retained for categorical variables and fivenum (i.e. Tukey's five numbers, minimum, quartiles and maximum) for continuous variables. When interactions = FALSE, variables_to_predict() will return a list of all individual variables used in the model. If interactions = FALSE, it will search for higher order combinations of variables (see model_list_higher_order_variables()).

variables_list's default value, "auto", calls variables_to_predict(interactions = TRUE) while "no_interaction" is a shortcut for variables_to_predict(interactions = FALSE).

You can also provide custom specifications (see examples).

plot_marginal_predictions() works in a similar way and returns a list of plots that could be combined with patchwork::wrap_plots() (see examples).

For more information, see vignette("marginal_tidiers", "broom.helpers").

See also

marginaleffects::avg_predictions()

Other marginal_tieders: tidy_all_effects(), tidy_avg_comparisons(), tidy_avg_slopes(), tidy_ggpredict(), tidy_marginal_contrasts(), tidy_marginal_means(), tidy_margins()

Examples

if (FALSE) { # interactive()
# Average Marginal Predictions
df <- Titanic |>
  dplyr::as_tibble() |>
  tidyr::uncount(n) |>
  dplyr::mutate(Survived = factor(Survived, c("No", "Yes")))
mod <- glm(
  Survived ~ Class + Age + Sex,
  data = df, family = binomial
)
tidy_marginal_predictions(mod)
tidy_plus_plus(mod, tidy_fun = tidy_marginal_predictions)
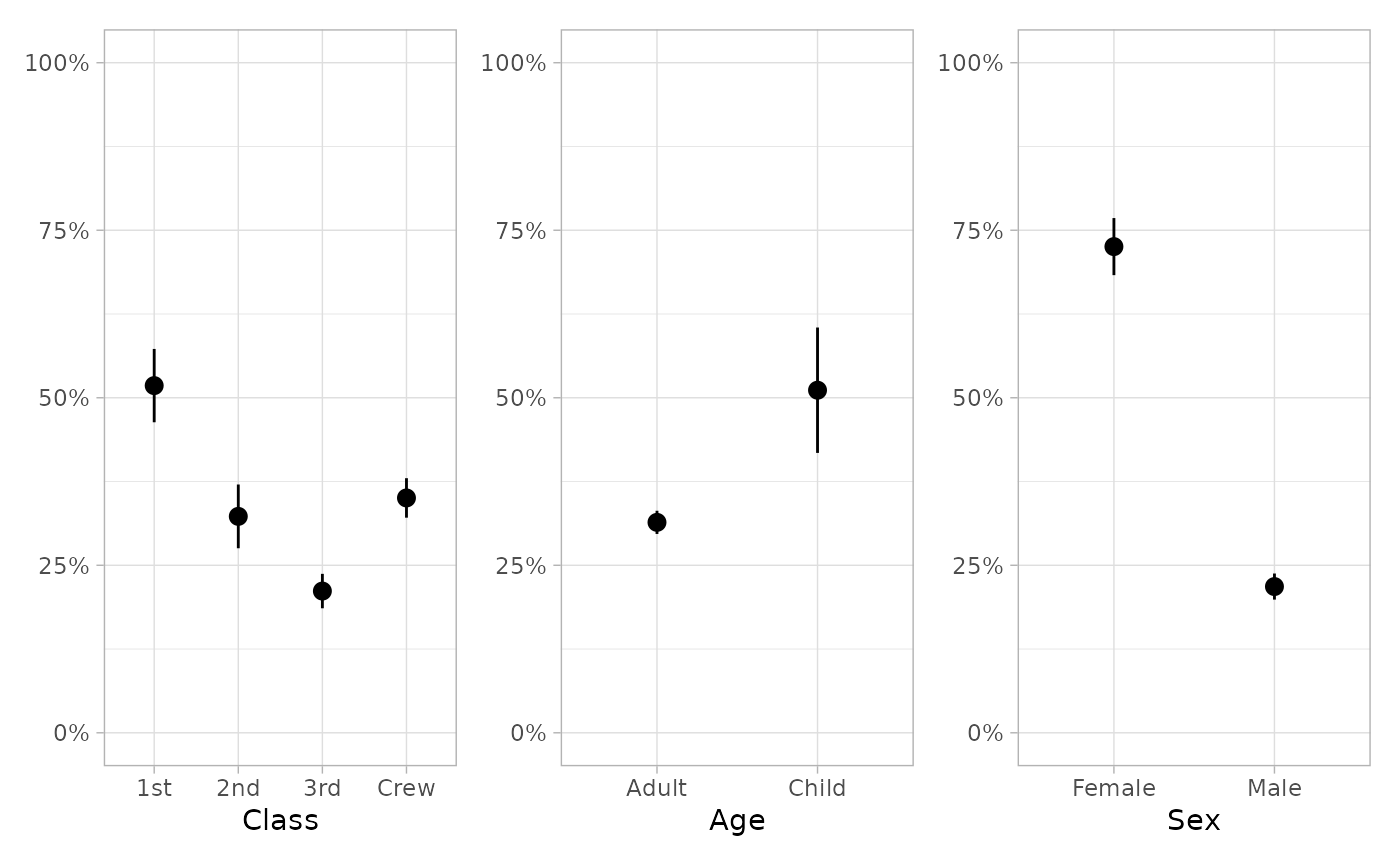
if (require("patchwork")) {
  plot_marginal_predictions(mod) |> patchwork::wrap_plots()
  plot_marginal_predictions(mod) |>
    patchwork::wrap_plots() &
    ggplot2::scale_y_continuous(limits = c(0, 1), label = scales::percent)
}

mod2 <- lm(Petal.Length ~ poly(Petal.Width, 2) + Species, data = iris)
tidy_marginal_predictions(mod2)
if (require("patchwork")) {
  plot_marginal_predictions(mod2) |> patchwork::wrap_plots()
}
tidy_marginal_predictions(
  mod2,
  variables_list = variables_to_predict(mod2, continuous = "threenum")
)
tidy_marginal_predictions(
  mod2,
  variables_list = list(
    list(Petal.Width = c(0, 1, 2, 3)),
    list(Species = unique)
  )
)
tidy_marginal_predictions(
  mod2,
  variables_list = list(list(Species = unique, Petal.Width = 1:3))
)

# Model with interactions
mod3 <- glm(
  Survived ~ Sex * Age + Class,
  data = df, family = binomial
)
tidy_marginal_predictions(mod3)
tidy_marginal_predictions(mod3, "no_interaction")
if (require("patchwork")) {
  plot_marginal_predictions(mod3) |>
    patchwork::wrap_plots()
  plot_marginal_predictions(mod3, "no_interaction") |>
    patchwork::wrap_plots()
}
tidy_marginal_predictions(
  mod3,
  variables_list = list(
    list(Class = unique, Sex = "Female"),
    list(Age = unique)
  )
)

# Marginal Predictions at the Mean
tidy_marginal_predictions(mod, newdata = "mean")
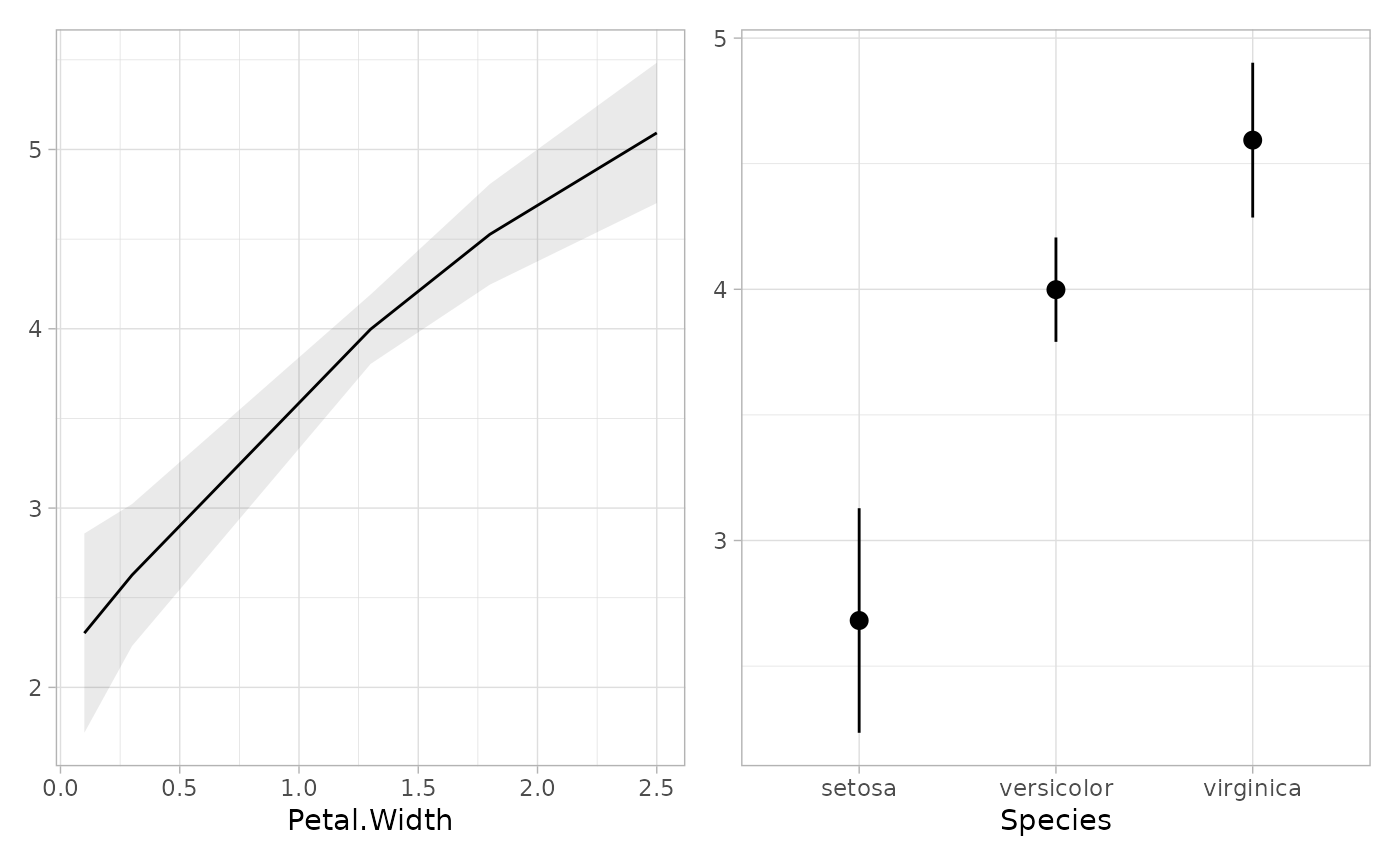
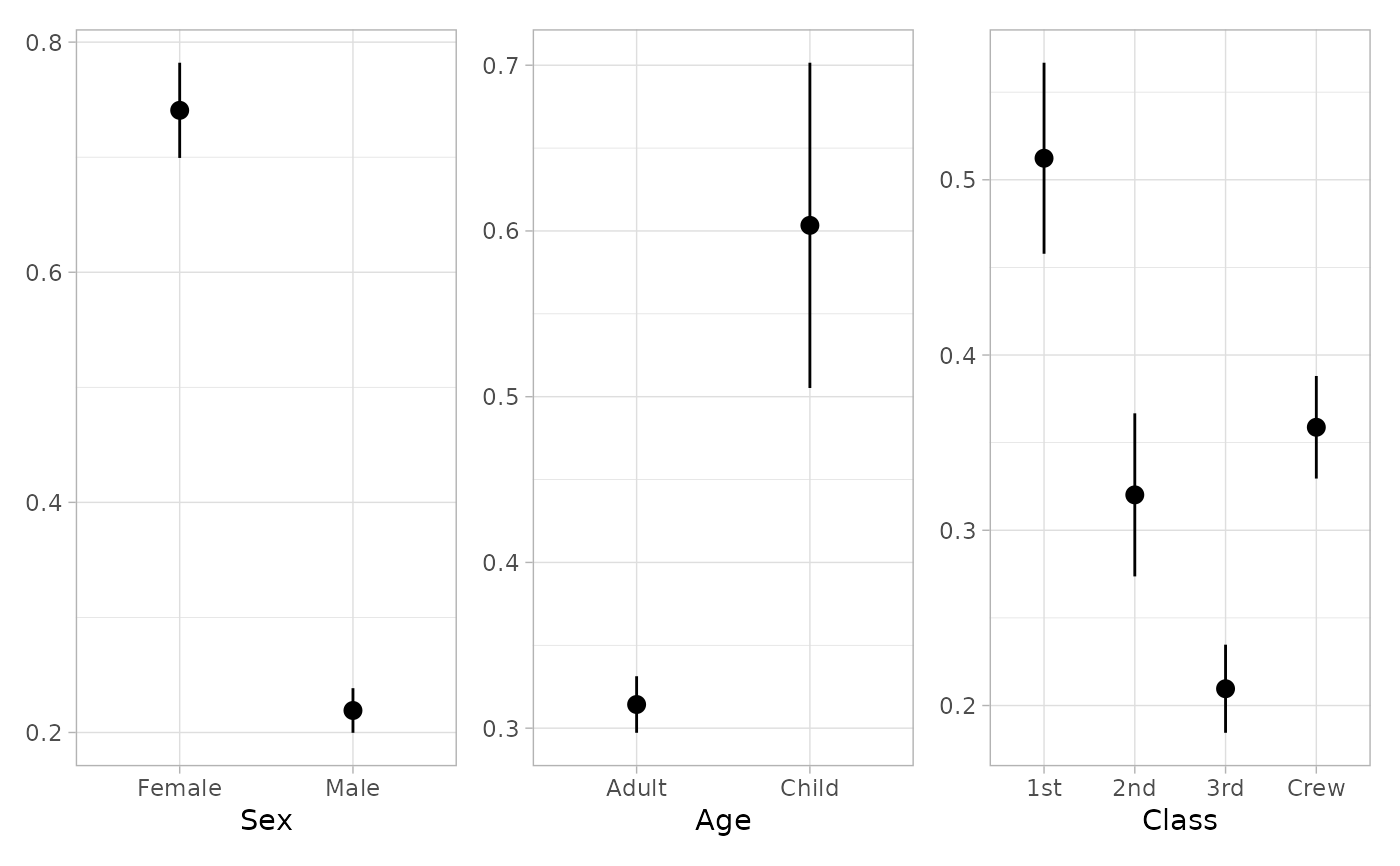
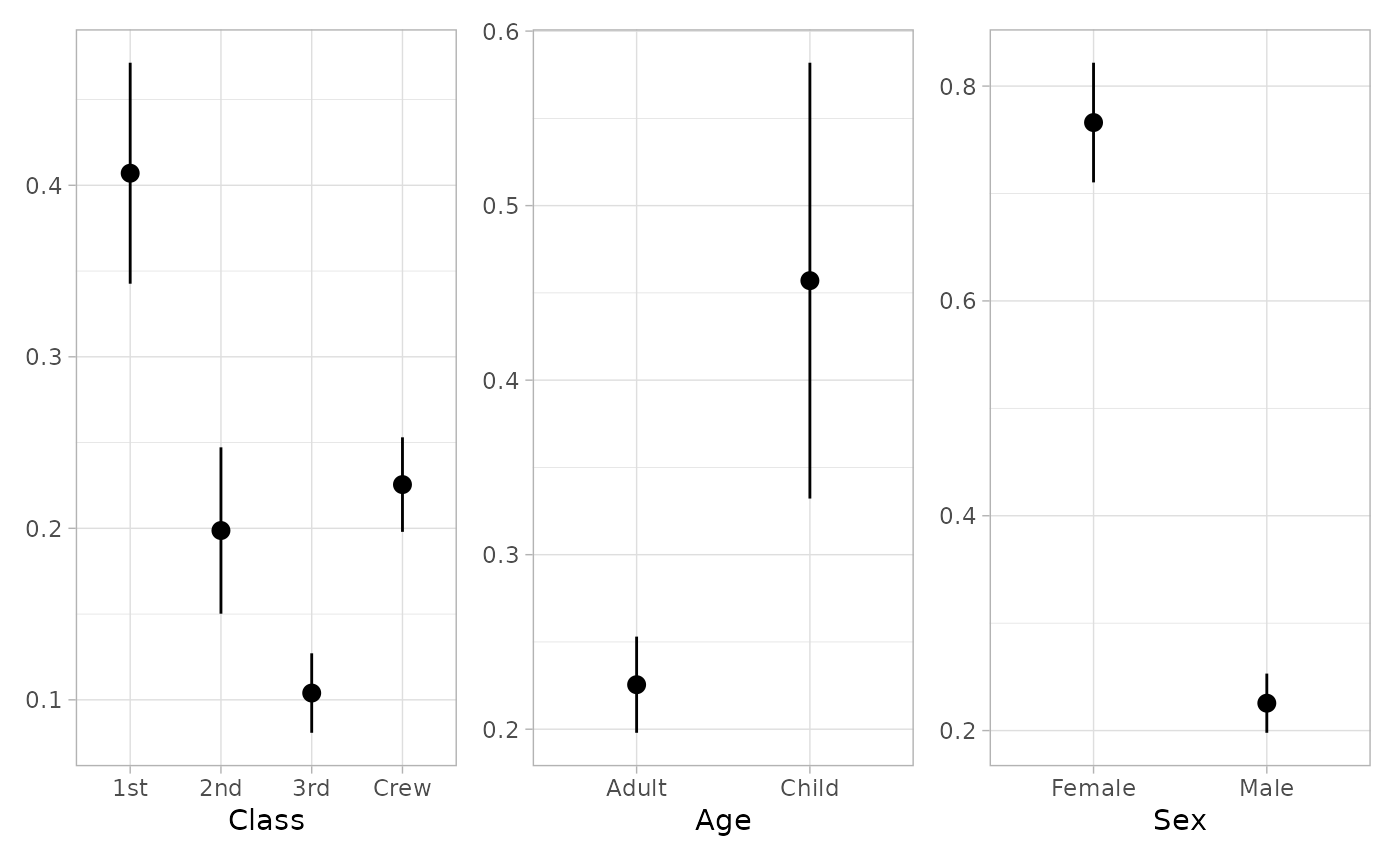
if (require("patchwork")) {
  plot_marginal_predictions(mod, newdata = "mean") |>
    patchwork::wrap_plots()
}
}